基于分位数回归的城市居民生活水价影响因素分析
(武汉科技大学冶金工业过程系统科学湖北省重点实验室, 武汉 430065)
基于分位数回归的城市居民生活水价影响因素分析
丁咏梅
(武汉科技大学冶金工业过程系统科学湖北省重点实验室, 武汉 430065)
水价是市场的方向标,其价格受多方因素影响。本文探讨了生活水价的影响因素,建立分位数回归模型,并从弹性的角度分析各个因素对生活水价的影响程度,比较了条件均值所反映的“平均水平”和不同分位数上的条件分布。结果表明:水资源费、固定资产折旧和大修理费用的变化对水价影响程度最大,水价中应适当增加人力成本,同时,需要提升人们的节水意识,提高固定资产的使用效率。
水价;分位数回归;分析
1 前 言
2011年1月发布的《中共中央国务院关于加快水利改革发展的决定》中指出:合理调整城市居民生活用水价格,稳步推行阶梯式水价制度。作为水市场的方向舵,水价在资源配置中有着至关重要的作用。因此,合理分析水价的构成及其因素间的相互关系、剖析水价的构成,对于提高用水效率、实现我国水资源的可持续利用有着非常重要的现实意义。
国内外众多学者围绕水资源的价值、价格、水价结构等进行了大量研究工作,取得了显著的研究成果。在国外,Roland K.[1]比较系统地介绍了城市水价的构成,Shanthi Nataraj[2]开发了自然实验来设计水资源的区域定价方案,并将双边边际水价应用于实际,使得圣克鲁斯的用户用水量下降了12%,有效节约了水资源;Lim[3]研究了城市供水系统,从而设计最优路径来减少环境污染和运输成本;Prakashan Chellattan Veettil等[4]研究了四种水资源定价方法,即面积定价、作物定价、区域定价和水量定价; D.V. Raje[5]和Roberto[6]研究了家庭居民对水价支付意愿及其影响因素;Garci等[7]从水资源供需角度建立了水价预测模型,确定了边际成本定价方法。在国内,李翠梅等[8]测算了2010年苏州市居民生活水价,并对预测后的水价进行回归分析,为城市水价收取与调整、水费管理与分配提供了新的依据;朱颖辉[9]运用Logistic回归分析了水厂的水质影响因素;常宝军[10]认为,水价是总量控制的有力抓手;刘小晖等[11]以新疆石河子市为例,通过抽样问卷调查、分析、综合评价等途径对生活用水进行了定价探析; 沈佩君、钟名军等[12-13]阐述了调水工程供水水价的组成;汪敏[14]在分析水资源需求和供给关系的基础上, 探讨了跨流域调水的水价定价策略;杨森等[15]运用拍卖理论建立了统一定价模型,得出了卖水方寻求最大化总利润实际上是基于用水户的虚拟估价而定价的结论;张新俊[16]认为,生活饮用水的水价中不应包含水资源费;王莉芳等[17]建立基于正态分布假设的城市居民用水阶梯水价计量模型并给出模型的评价标准,对城市居民用水的不同阶梯定价模式进行了评价;陈易等[18]指出,水价完全成本应该由资源水价、工程水价、环境水价、边际使用成本4部分组成;王谢勇等[19]利用模糊数学、边际机会成本等理论构建了水价动态完全成本定价模型;高兴佑、高文进[20]提出了完善城市水价制度的措施;刘正洪、姜斌[21]认为,目前我国水价机制比较突出的问题有:部分地区水价偏低,水价成本约束机制尚未健全,水价秩序不规范,水价结构不合理,需要发挥市场基础性作用,改革价格管制;推进供水企业产权改革和经营体制改革;建立合理的补偿机制。
综合上述文献可知,国内外学者们大多关注的是水价的构成、水价预测等方面的研究,从博弈学、经济学、环境科学等专业上去解释水价的结构,预测某个城市未来水价的走向,一方面为资源的合理利用提供了依据,另一方面促使人们有支付意愿。水价是市场的方向标,其价格由多方因素合成。目前我国城市实行阶梯水价,包括家用水价、工业水价和商业水价等。不同领域的水价构成因素各异。本文从统计学角度,应用分位数回归理论,考虑不同分位数上的条件分布,分析城市居民生活水价的构成因素及其关系,同时,为水价的调整提供科学依据。
2 变量的选择及数据来源
2.1 变量的选择
参考水利部人事司李华在《水价改革政策及面临问题的解决对策》一文中[22]提出的城市水价的成本核算方法,同时,结合文献[8]可知,城市生活水价由固定成本和可变成本构成。其中,固定成本包括括工人工资及福利、固定资产折旧、无形资产与递延资产摊销费、大修理费和日常修理费用等;可变成本包括水资源费、动力费用、药剂费用、管理费用和财务费用等五个方面。
2.2 数据来源
本文数据来源于文献[8],其固定成本和可变成本在水价中的比重如下页图1、图2所示。
3 模型设定及参数估计
传统的水价回归分析通常采用普通最小二乘法来估计参数,往往只能得到一组参数估计值, 其回归结果的含义是在给定解释变量的条件下对被解释变量的平均水平的估计。普通最小二乘法估计不能更深入地分析不同分位点上解释变量与被解释变量以及解释变量间不同的相关关系。为了克服这种缺陷,Koenker和Bassett(1978年)提出了分位数回归。
分位数回归是依据因变量的条件分位数对自变量X进行回归,这样得到了所有分位数下的回归模型,分位数回归能够捕捉分布的尾部特征。因为对模型中的随机扰动项不需作任何分布的假设,从而使得分位数回归系数估计比OLS回归系数估计更稳健。同时,分位数回归估计出来的参数具有在大样本理论下的渐进优良性[23],其在国内外的应用可参见文献[24-25]。
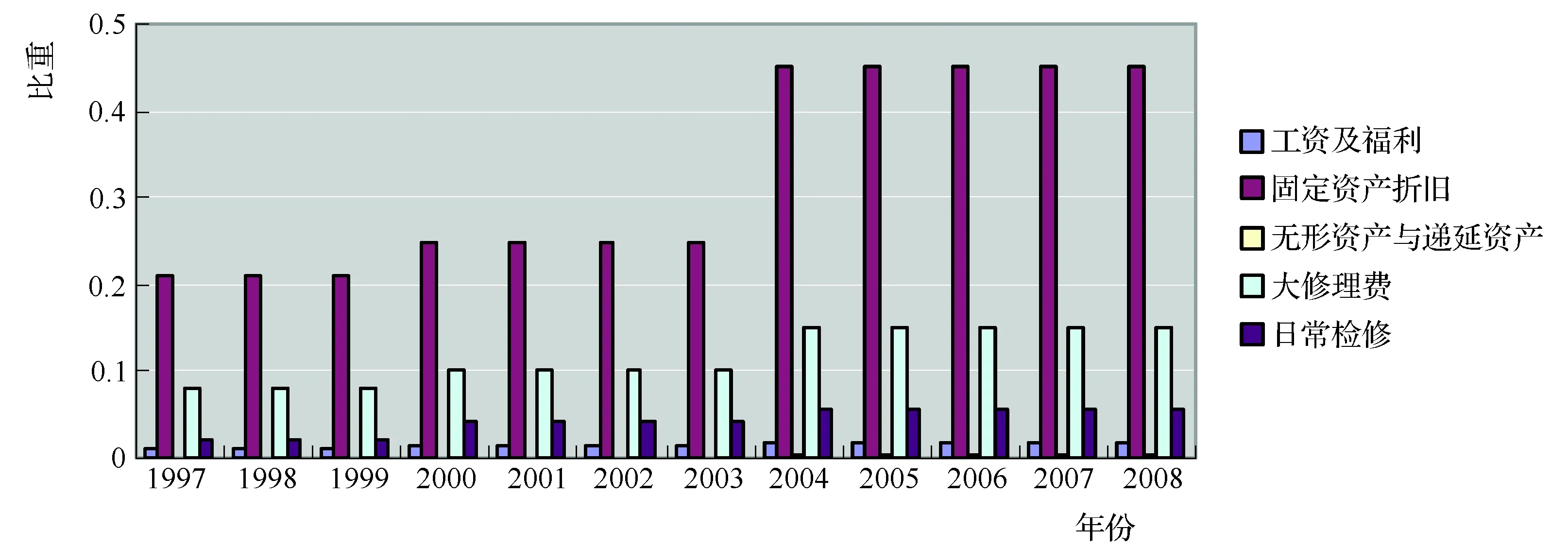
图1 1997~2008年各年中固定成本在水价中的比重

图2 1997~2008年各年中可变成本在水价中的比重
3.1 模型设定
定义1[26]对∀τ∈(0,1)及随机变量Y,Y的τ分位数定义为:对任意ξτ∈R,满足下式:
P(Y<ξτ)≤τ≤P(Y≤ξτ)
定义2[26]由定义1,可得出分位数函数Q为一左连续函数,即
|FY(y)≥τ),0<τ<1
定义3[26]称

3.2 参数估计
分位数回归的基本原理是通过使加权误差绝对值之和最小来得到参数的估计。对于∀τ∈(0,1),参数βτ可由下式估计得到[26]:
其中ρτ(u)=u[τ-I(u<0)],0<τ<1
4 实证分析
结合文献[8]的数据,应用EVIEWS6.0对影响水价的10个主要因素进行分析,用Bootstrap算法来估计回归参数。为了更好地反映各个因素的变动对价格的影响力度,先对数据进行了取对数处理,从而回归系数就可以反映各个因素在不同的分位点处的弹性变化,以此来说明该因素的调节力度大小对水价的影响程度。下表为各分位点处的回归结果。
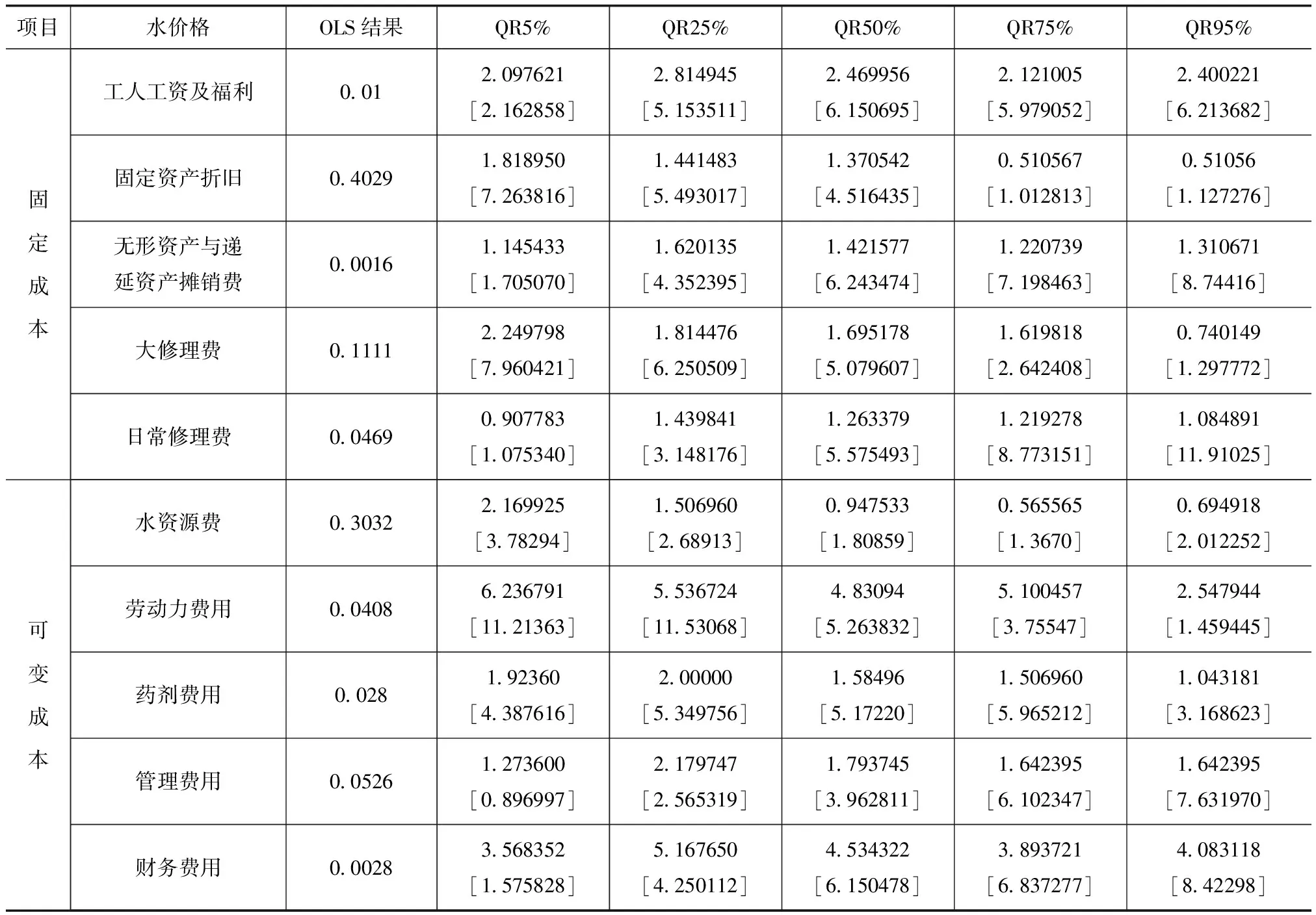
各因素对水价的分位数回归结果表
上表中,OLS结果由文献[8]得到。我们知道,传统的线性回归是刻画自变量的变动对因变量均值的影响,是从平均水平角度刻画变量间的线性关系,从上表中的第二列可知,OLS只是给出了各个影响因素对水价的平均影响,无法详细刻画不同水平上的具体影响程度,而分位数回归恰好弥补了这一不足。它可以刻画各个分位数处自变量对因变量的影响大小。因为篇幅有限,本文仅列出5%、25%、50%、75%、95%分位的系数及其T统计量值(方括号中的数值)。为了更清楚地说明问题,下页图3展示了各个影响因素的99个分位数处的弹性变化。
从图3中可以看出,各个分位数的回归系数都非常显著。水资源费、固定资产折旧和大修理费用的变化对水价的影响程度最大,并且都呈现出递减趋势,在大分位数阶段,固定资产折旧和大修理费用的弹性都小于1,说明当水价较高时,征收的水费中应适当调整固定资产折旧和大修理费用;财务费用、工人工资及福利、无形资产与递延资产摊销费和日常修理费用对水价的影响力度不大,而劳动力费用和管理费用对水价的影响呈现递增的趋势,说明在水价调整中,人力成本所占的比例要逐渐增大。
5 结 语
合理的价格对于资源的配置和社会的和谐至关重要,特别是对于日益匮乏的水资源。本文从计量经济学的角度,建立分位数回归模型,并从弹性的角度分析各个因素对水价的影响程度,比较了变量间均值所反映的“平均水平”和不同分位数上的条件分布结果。分位数回归更加细致地刻画了在不同的水平上,自变量对因变量的影响程度,从而使得水价的调整更有针对性,对水市场的建设起到一定的参考作用。

图3 各个因素的弹性对因变量的影响
[1]Roland K. Urban Hydroinformatics,Data, Models and Decision Support for Integrated Urban Water Management[M]. Price, Zoran Vojinovic, IWA Publishers, 2011.
[2]Shanthi Nataraj, W.Michael Hanemann. Does marginal price matter? A regression discontinuity approach to estimating water demand[J]. Journal of Environmental Economics and Management, 2011, 61:198-212.
[3]Lim.S.R.,Suh. S.,Kim J.H.,et al. Urban water infrastructure optimization to reduce environmental inpacts and costs[J].Journal of Environmental Management,2010,91(3):630-637.
[4]Prakashan Chellattan Veettil, Stijn Speelman, Aymen Frija, et.al. Complementarity between water pricing, water rights and local water governance: A Bayesian analysis of choice behaviour of farmers in the Krishna river basin, India[J]. Ecological Economics,2011,70:1756-1766.
[5]D.V. Raje, P.S. Dhobe, A.W. Deshpande. Consumer’s willingness to pay more for municipal supplied water: a case study[J]. Ecological Economics,2002,42: 391-400.
[6]Roberto G.A.,Jal R.L.Dirived willingness-to-pay for household water use with price and probabilistic supply[J].Journal of Water Resources Planning and Management,2006,132(6): 424-430.
[7]Serge .G.,Arnaud R. Estimating the benefits of efficient water pricing in France[J].Resource and Energy Economics,2004,26(1):1-25.
[8]李翠梅,王建,王浩,刘遂庆.城市居民生活水价测算的回归分析[J]. 兰州理工大学学报,2011,37(5):121-125.
[9]朱颖辉. 出厂水水质影响因素的Logistic回归分析[J]. 浙江预防医学,2010,22(1):48-49.
[10]常宝军,李文安.水价是总量控制的有力抓手——基于“一提一补”理论[J].给水排水动态,2011(2):16-18.
[11]刘小晖,张满银,王得楷,龚琪.公众参与城镇居民生活用水水价探析[J]. 中国农村水利水电,2011(12):68-75.
[12]沈佩君, 郭元裕, 张志明. 跨流域调水工程供水水价研究[J] . 水利经济, 1999(3): 38-42.
[13]钟名军, 郑雄伟, 周芬.跨流域调水工程供水水价实例研究[J]. 中国农村水利水电,2011(2):109-111.
[14]汪敏.跨流域调水水价的影响因素分析[J]. 水利经济,2009,27(3):38-41.
[15]杨森, 王先甲, 周彦辰, 焦健. 基于拍卖理论的水价研究[J]. 武汉大学学报(工学版),2011,44(2):187-191.
[16]张新俊.生活饮用水的水价中不应包含水资源费[J].价值工程,2011,30(10):3-4.
[17]王莉芳,陈春雪,熊霆.城市居民用水阶梯水价计量模型及应用[J].长江会科学院院报,2011,28(5):5-8.
[18]陈易, 安子琴,姜小川,王谢勇.基于完全成本定价模型的大连市水价研究[J].水利经济,2011,29(3):42-45.
[19]王谢勇, 谭欣欣,陈易.构建水价完全成本定价模型的研究[J]. 水电能源科学,2011,29(5):109-112.
[20]高兴佑,高文进.基于完全成本和边际机会成本的城市水价研究[J].人民黄河,2011,33(7):90-92.
[21]刘正洪,姜斌.我国城乡供水水价机制初探[J].中国水利,2010(6):41-43.
[22]李华.水价改革政策及面临问题的解决对策[J].中国水利,2010(2):61-64.
[23]Koenker R. and G. Bassett, Jr. Regression quantiles[J]. Econometrica,1978,46:33-50.
[24]陈建宝,丁军军.分位数回归技术综述[J].统计与信息论坛,2008,23(3):89-96.
[25]李育安.分位数回归及应用简介[J]. 统计与信息论坛,2006,21(3):35-38.
[26]Niels Schulze.Applied Quantile Regression:Microeconometric,Financial,and Environmental Analyses[M].Tubingen,2004.
AnalysisofInfluenceFactorsonUrbanCitizenLivingWaterPriceBasedonQuantileRegression
DING Yong-mei
(MetallurgicalIndustryProcessSystemScienceHubeiKeyLaboratoryofWuhanUniversityofScience,Wuhan430065,China)
Water price shows market direction, which is affected by various factors. Influence factors of living water price are discussed in the paper. Quantile regression model is established. The influence degree of various factors on living water price is analyzed from flexibility point of view. ‘Average level’ reflected by condition mean is compared with condition distribution on different quantiles. The results show that water resource fee, depreciation of fixed assets and overhaul cost change have the greatest impact on water price. Labor cost should be suitably increased in water price. Meanwhile, people’s awareness of water conservation should be improved, and efficiency in the use of fixed assets should be improved.
water price; quantile regression; analysis
F29
A
1673-8241(2014)1-0050-06

