基于二分法识别拉索索力与抗弯刚度

施 政，颜全胜

(华南理工大学土木与交通学院，510640，广州)

基于二分法识别拉索索力与抗弯刚度

施 政，颜全胜*

(华南理工大学土木与交通学院，510640，广州)

采用二分法对拉索的索力与抗弯刚度进行同时识别，来满足桥梁工程中快速、准确的识别索力与抗弯刚度的要求。通过将频率方程进行数学上的处理和简化，成为简化的频率方程，并考虑初等函数曲线的性质，采用二分法在指定区间内迭代的方法，求解该简化方程的根，可以实现由索力求解任意阶的频率，或由至少2阶(频阶任意)的频率识别索力和抗弯刚度。在Excel中建立数值拉索，利用其VBA平台，编程实现了该方法的自动计算；与ANSYS结果对比，表明精度满足工程要求。

频率法；二分法；索力；抗弯刚度；参数识别；VBA

0 引言

频率法测得各阶频率之后，如何识别未知的索力和抗弯刚度，是索力测试中最主要问题之一。索力的计算是基于抗弯刚度值的，因此精确的识别抗弯刚度，保证索力识别的准确性，是十分重要的。由于索的内部平行钢丝束之间相互挤压而并非完全粘结，索弯曲过程中由于相对位移而产生摩擦，索外包聚乙烯保护层和索内部其他构件等均有抗弯刚度等诸多原因，导致索的抗弯刚度是介于零和同截面特性的梁的抗弯刚度之间的数，无法精确确定。

对于物理刚度较大，两端固支的短索，特征参数ξ较小的索而言，抗弯刚度的不精准，将导致较大的索力计算误差。

识别抗弯刚度EI的前提是能够计算对应于各阶频率fn的索力Tn。许多学者已研究并推导了由频率求索力的经验公式，但其中多数不能由高阶频率计算索力，且有其特定的ξ适用范围，有的对于ξ大的索识别准确，有的对于ξ小的索识别准确。

Hiroshi Zui[1]等通过绘出两端固支索频率方程的解曲线并进行曲线拟合，得到精度较高的经验公式，但公式基于1阶和2阶频率求索力，采用高阶频率计算索力需要ξ>200；任伟新、陈刚[2]基于能量法与曲线拟合法得出由基频计算索力的经验公式，只能通过基频求索力；邵旭东[3]基于能量法和索的一阶振型函数得到由刚性吊杆基频计算索力的公式，但该公式的准确性与参数G有关，而G随拉索参数不同而变化，引起精度的不稳定；孟少平[4]通过一、二阶频率计算索力，避开了抗弯刚度的问题，但该式只能用第一、二阶频率计算索力，且不能识别抗弯刚度。魏金波[5]提出了对频率方程进行简化的思路，苏成[7]提出了同时识别索力和抗弯刚度的方法，但使用的是3次样条拟合技术且需要进行有限元分析，且试算索力与抗弯刚度均采用定步长法，其搜索效率低于二分法。

本文综合文献[5,7]的思路和方法，采用二分法[8]直接对非线性方程进行迭代求根，并利用Excel表格中的VBA功能编制程序，实现方便快捷的进行索力与抗弯刚度的识别。

1 索的特性

1.1索参数说明

本文中用到的主要参数包括：T=索力；EI=索的抗弯刚度；EIfac=抗弯刚度折减系数；l=索的长度；m=索的单位长度质量；n=频阶；ωn=第n阶圆频率；fn=第n阶频率；Tn=由频率fn计算的第n阶索力；αl=文中构造函数的自变量；ξ=无量纲参数。

工程中的索各式各样，索的特性各不相同，但频率-索力曲线的样式不同，其本质在于特征参数ξ不同[6]。

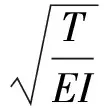
(1)

2 不同边界索的频率与索力求解

本文研究的索为小垂度索在xy平面内的振动。索的频率方程写为式(2)，其中y(x,t)为索的横向位移坐标，x为沿索纵向坐标，φ(x)为振型函数，h(t)为索力随索振动时的变化量，这里忽略它取h(t)=0，其他参数见1.1节。

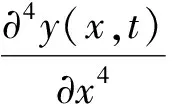
(2)

φ(x)=C1sinαx+C2cosαx+C3sinhβx+C4coshβx

(3)

根据不同的边界条件求出系数C1～C4，得到频率方程。以下重点研究两端固支边界和一端简支一端固支边界的拉索的索力和抗弯刚度识别。

2.1两端固支索

两端固支索的频率方程[1]如式(2)。

2(αl)(βl)[1-cos(αl)cosh(βl)]+[(βl)2-(αl)2]sin(αl)sinh(βl)=0

(4)

各参数表达式如式(3)。

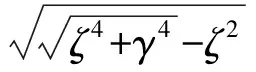
(5)

(6)

(7)

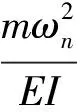
(8)

ωn=2πfn

(9)

该方程为隐式超越方程，由于双曲正弦、余弦函数带来的强烈的非线性。直接使用N.R迭代法求解，如果给定的迭代初值x0不足够靠近零点，初值处的切线斜率易趋于无穷大f′(x0)→∞，于是之后一系列迭代点xn始终在初值x0附近不下降，切线斜率始终很大，如此恶性循环以致收敛速度极为缓慢。然而，若采用不需要导数的二分法进行迭代即可避免上述问题。

根据文献[5]的简化法，当ξ较大时，结合双曲正弦、余弦函数的性质，和βl的表达式，可以近似认为式(10)～式(12)的假定成立。

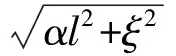
(10)

cosh(βl)≈sinh(βl)

(11)

2αβ=0

(12)

于是，在式(10)～式(12)假定下，频率方程可简化为式(13)，并写成等号一边为正弦函数，另一边为关于αl表达式的形式

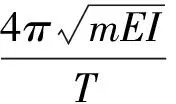
(13)

2.1.1 求解频率 已知索力T、抗弯刚度EI，求第n阶频率fn。

由式(5)得到

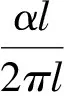
(14)

将式(14)代入式(13)化简得到

(15)

构造2个关于αl的函数

h(αl)=tan(αl)

(16)

(17)

则方程(15)的求根的问题转化为求函数h(αl)和g(αl)的交点问题，两函数图像见图1。

图1 h(αl)&g(αl)～αl图像两端固支索求频率

根据表达式(17)，αl≥0时，g(αl)是αl=0

处略低于抛物线，而随着αl的增大不断逼近函数p(αl)的近似二次函数，在(0,+∞)上递增。

由式(14)，αl与fn增减性相同，fn随n增大而增大，且在αl≥0时，由图1，随着αl增大，两函数的第1个交点在n=1的区间内，n>1的每个区间内有且仅有一个交点，可推得第n阶频率对应于第n个区间内的交点。

因此求解流程如下：

f(αl)=h(αl)-g(αl)

(18)

2)将αl结果与已知索力T代入式(14)求fn。

2.1.2 求解索力 此时已知索的第n阶频率fn和抗弯刚度EI，要求对应的索力Tn。

由式(5)得

(19)

将式(19)代入式(13)化简后得

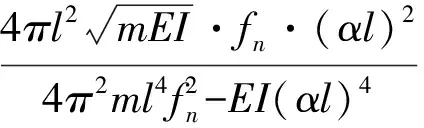
(20)

构造2个关于αl的函数

h(αl)=tan(αl)

(21)

(22)

则求解方程(20)的根的问题转化为求函数h(αl)和g(αl)的交点问题，图2为两函数的图像。

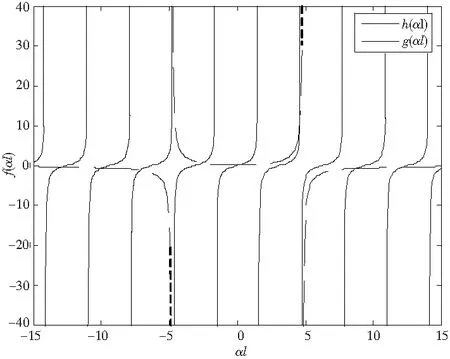
图2 h(αl)&g(αl)～αl图像两端固支索求索力

对于g(αl)，令分母为零时的αl取值为αlA，则有

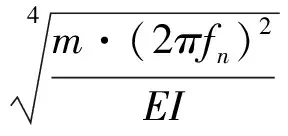
(23)

即g(αl)在αlA处不连续。因αl≥0，对g(αl)求导易得g′(αl)>0，所以g(αl)为关于αl的在(0,αlA),(αlA,+∞)上的递增函数，且在区间(0,αlA)上g(αl)>0，在区间(αlA,+∞)上g(αl)<0。

1)推导间断点所在区间的区间号nA，它需要满足式(24)，解出nA表达式(25)，Int表示取整；

(24)

(25)

2)由于两函数在n=nA的区间无交点，在n>nA的每个区间只有一个交点，因此当n≥nA时，需要前移一个区间即令n=n+1，再求解。

3)根据式(29)，当αl>αlA时，会有Tn<0，其物理意义是，因为目标频率太小，以至于当索受到轴向压力时，频率才能达到如此小。拉索是受拉的所以索力不能取负值。在迭代求EI过程中，一旦出现Tn<0，则EI肯定偏大，无需再计算，可直接二分法减小EI识别值，再重新迭代。

因此计算步骤为：

1)由式(25)计算nA；

f(αl)=h(αl)-g(αl)

(26)

3)将αl结果与已知频率fn代入式(19)求Tn。

2.2一端简支一端固支索

修改边界条件，推导出频率方程如式(27)，该式变形为式(28)，其中参数的表达式见式(5)～式(9)。

βlsin(αl)cosh(βl)-αlcos(αl)sinh(βl)=0

(27)

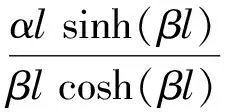
(28)

类比2.2节的方法，构造两函数

h(αl)=tan(αl)

(29)

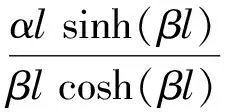
(30)

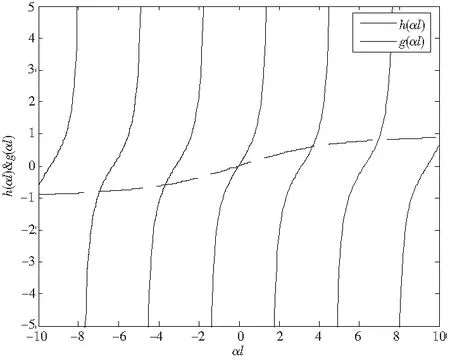
图3h(αl)&g(αl)～αl图像一端固支一端铰支求频率

2.2.1 求解频率 将式(10)代入式(30)得到式(31)

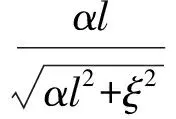
(31)

2)将得到αl代入式(14)计算频率fn。

2.2.2 求解索力 由式(19)代入式(1)变形为式(32)，代入式(30)得

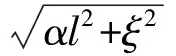
(32)

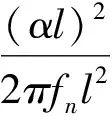
(33)

2)将1)中得到的αl值和已知频率fn代入式(19)计算索力Tn。

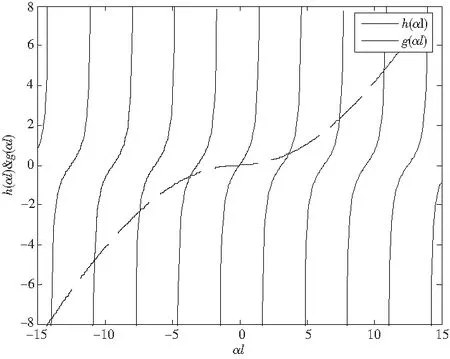
图4h(αl)&g(αl)～αl图像一端固支一端铰支求索力

3 二分法迭代的参数识别流程

二分法迭代的优点是迭代次数较少、稳定、收敛性较好，能够保证迭代终值的精度，迭代次数由精度决定，达到1E-6精度平均迭代次数为log2106=19.93。因此，采用二分法迭代对简化方程式(14)求根。识别索力与抗弯刚度的算法流程图如图5。

算法包括两重循环：1)外循环，由fn求Tn；2)内循环，由Tn求EI。

算法关键的二分法调整步骤用伪代码描述：

1)EIfac的上下限初值：EImin=0,EImax=0。

2)根据计算得到拟合直线斜率值k用二分法调整EIfac上下限：由于索力只有一个值，因此取得正确EIfac时，各阶Tn应该相同，即k=0。当k>0说明EI偏小，则令EImin=EIfac；当k<0说明EI偏大，则令EImax=EIfac。

3)αl的上下限初值：

4)根据f(αl)调整上下限：如果f(αl)>0，说明αl偏大，则令almax=αl；如果f(αl)<0，说明αl偏小，则令almin=αl。

5)为减少误差，T取为各阶Tn的平均值。

4 数值拉索测试

4.1建立拉索

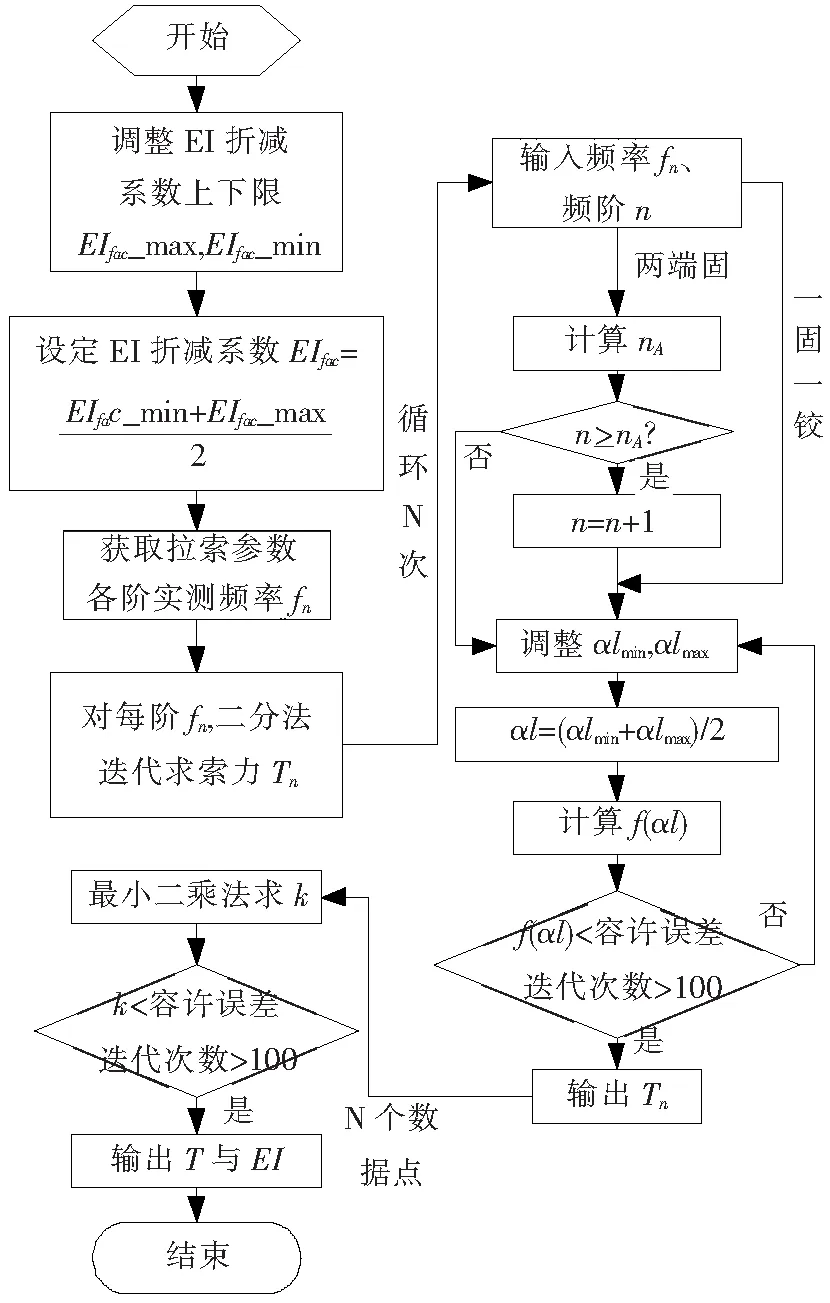
图5 二分法参数识别流程图

建立9根数值拉索如表1所示，满足ξ=1～500，边界为固支和一端固支一端铰支；小垂度索需满足垂跨比δ=s/l0≪1，注意控制等效弹模Eeq非常接近于弹模E=1.8E11，拉索应力小于容许应力σ<1.86E9Pa(1 860 MPa)。

4.2编制程序

在Excel的VBA平台用Visual Basic语言编程识别边界为固支、一端固支一端铰支拉索的频率计算程序，和索力、抗弯刚度的识别程序。

4.3频率计算

在ANSYS中，对已经建立的数值索，进行模态分析，得到模态频率(由有限元计算)；在Excel中，根据输入的拉索参数(已知索力与抗弯刚度)，计算各阶频率；对每一根索，将在ANSYS中计算的模态频率与Excel中计算的频率比较，如表2所示。

4.4索力和抗弯刚度识别

将ANSYS计算得到的n阶频率作为实测频率，采用Excel中程序计算，得到索力与抗弯刚度的识别值，将该识别值与建模时的真实值比较，结果如表3所示。

分析表2中数据得到结论：

1)由表2知，本文方法的频率计算误差与ANSYS结果相比小于0.3%，精度满足工程要求；

2)由表2知，索力识别误差小于1%，抗弯刚度识别误差小于0.3%，精度满足工程要求。

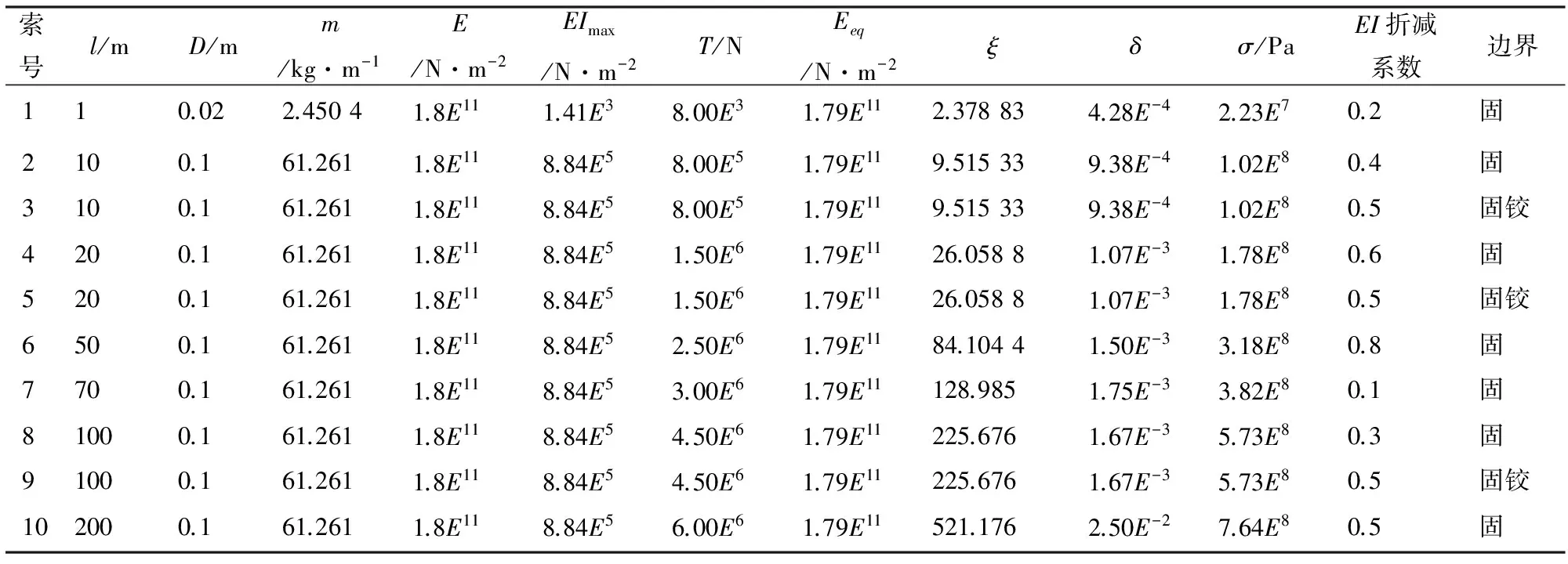
表1 数值索的各项参数

表2 Excel与ANSYS的1～3阶频率结果比较、索力与抗弯刚度的识别结果

5 工程拉索测试

范和港斜拉桥位于广东省惠州市惠东县巽寮湾，为主跨300 m的双塔单索面斜拉桥，两塔的中跨和边跨均设23对斜拉索，索的特征参数在之间，索力设计值在1 986～4 038 KN之间。

采用频率法识别索力，取短索、中长索、长索各1根，边界为两端固支，分别用Zui公式[1](带入抗弯刚度折减系数0.6)以及本文公式，根据实测频率计算索力、抗弯刚度折减系数，并对比列于表3。

图6 范和港斜拉桥

图7 拾取振动信号

由表3知，本文的索力计算结果与Zui公式索力计算结果的误差在0.1%以内，识别得到的各索的抗弯刚度均在0.6EI0左右，且其误差随着索的特征参数的增大而增大，说明本文方法的计算结果较为精确，进一步说明识别抗弯刚度折减系数时，要使用特征参数小的索才能得到较高精度。这是由于特征参数小的索的几何刚度所占比例偏小，物理刚度所占比例偏大，因此其频率对抗弯刚度的灵敏度较高，识别较为精确；特征参数大的索的几何刚度所占比例偏大，物理刚度所占比例偏小，因此其频率对抗弯刚度的灵敏度很低，识别精度偏低。

表3 模态频率计算结果对比

6 结论

1)本文方法只适用于求解两端固支或铰支的小垂度拉索，理论上可求解任意指定的频阶n的索力Tn和频率fn，与有限元索力和频率结果的误差普遍小于1%。

2)本文方法无需输入索力预估值，即可识别索力，避免了索力预估值错误导致索力识别错误的潜在风险。

3)输入的实测频率，频阶可以是任意的(至少2个，互不重复)，优于文献[2]、[3]中只能根据基频或二阶频率进行索力识别。

4)采用二分法迭代的收敛速度快且稳定，计算精度高于多数拟合公式的精度，且适用于特征参数ξ>2的拉索，适用范围广。数据的输入和输出过程集成在Excel环境中，拉索参数，实测频率与索力、抗弯刚度计算结果方便于查看与修改，工程实用性强。

[1] Hiroshi Zui,Tohru Shinke,Yoshio Namita.Practical Formulas for Estimation of Cable Tension by Vibration Method[J].Joumal of Structural Engineering,ASCE,1996,122(6):651-656.

[2]任伟新,陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报,2005,38(11):26-31.

[3]邵旭东, 李国峰, 李立峰. 吊杆振动分析与力的测量[J].中外公路,2004,24(6):29-31.

[4]孟少平,杨睿,王景全.一类精确考虑抗弯刚度影响的系杆拱桥索力测量新公式[J].公路交通科技,2008,25(6):87-98.

[5]魏金波.弹性支承钢索受力动力检测理论和试验研究[D].上海:同济大学,2009.

[6]Irvine H M.Cable Structures[M].Cambridge,MA:The MIT Press,1981.

[7]苏成,徐郁峰,韩大建.频率法测量索力中的参数分析与索抗弯刚度的识别[J].公路交通科技,2005,22(5):75-78.

[8]Li F C,Zhang L N,Tian S Z,etal.Analysis of Identified Cable Force of Cable-Stayed Bridge[C].International Conference on Transportation Engineering,2009:3020-3025.

[9]Song Y,Cui X P,Lei Y,etal.Intelligent Sensors with Application to Identify the Steel Cable Forces[C].Earth and Space,ASCE:2010,1626-1633.

[10]朱铁诚.拉索参数识别的多频率法研究与索力无线监测系统开发[D].杭州:浙江大学,2010.

[11]魏金波,段欣.考虑抗弯刚度的索力动力检测法[J].陕西理工学院学报(自然科学版),2009,25(3):30-33.

[12]Ren W X,Hu W H.Cable modal parameters identification[J].Journal of Engineering Mechanics,2009,135,(1):51-61.

IdentificationofCableTensionandFlexuralRigiditybyDichotomyMethod

SHI Zheng,YAN Quansheng*

(School of Civil Engineering and Transportation,South China University of Technology,510640,Guangzhou,PRC)

Dichotomy method is used in cable parameter identification,in order to satisfy the need of identifying cable tension and flexural rigidity quickly and accurately.A simplified frequency equation can be acquired by adopting mathematical treatment and simplification to the frequency equation.Taking the property of elementary function curve into consideration,dichotomy method is adopted to find the solution of simplified frequency equation in specified interval according to frequency mode,to realize the identification of cable tension and flexural rigidity according to at least 2(or more) arbitrary modes of frequency.Cable frequency of arbitrary mode can also be calculated according to given cable tension and flexural rigidity.Numeric cables are created in Excel and a program is developed base on VBA platform to implement the parameter identification automatically.The calculation result compared to ANSYS result,shows that the identification error satisfies the engineering demand.

vibration method;dichotomy method;cable tension;flexural rigidity;parameter identification;VBA

2014-08-26;

2014-09-28

施 政(1991-)，男，江西南昌人，硕士研究生，研究方向：拉索参数识别研究。

国家自然科学基金项目(11202080)；广东省交通运输厅科技项目(科技-2012-02-024)。

10.13990/j.issn1001-3679.2014.05.020

U433.38

A

1001-3679(2014)05-0667-07

*通讯作者：颜全胜(1968-), 男, 博士, 教授; 主要从事大跨度桥梁研究， E-mail:cvqshyan@scut.edu.cn。