Mobile Path Selection Algorithm of Sink Node for Optimizing Network Lifetime*

WANG Zhangquan，CHEN Yourong，YU Lizhe，REN Tiaojuan

(College of Information Science and Technology，Zhejiang Shuren University，Hangzhou 310015，China)

Mobile Path Selection Algorithm of Sink Node for Optimizing Network Lifetime*

WANG Zhangquan，CHEN Yourong*，YU Lizhe，REN Tiaojuan

(College of Information Science and Technology，Zhejiang Shuren University，Hangzhou 310015，China)

To overcome the energy hole problem in wireless sensor networks，optimization method is used and mobile path selection algorithm of Sink node for optimizing network lifetime(MPSA)is researched.In MPSA algorithm，the monitoring area of single-hop transmission wireless sensor network is divided into multiple grids of same size.Sink node can move to any grid’s center and stay to gather data in the single-hop maximum communication range.Full node coverage condition of stay location and node energy consumption are analyzed.Then the optimization model which weighs network lifetime and mobile journey is established.The modified genetic algorithm is proposed to solve the model.The steps such as chromosome evaluation，selection，crossover，mutation，minimum coverage processing and isolated nodes processing are iteratively executed.Finally the mobile scheme of Sink node for optimizing network lifetime is obtained.Simulation results show that MPSA algorithm can improve the network lifetime and keep mobile journey at small range.In the aspect of improving network lifetime，it is better than RCC(range constrained clustering)algorithm.

wireless sensor networks;network lifetime;path selection;optimization algorithm

无线传感网WSNs(Wireless Sensor Networks)主要由分布在监测区域内的大量传感节点、Sink节点和监控中心组成。传感节点监测各种环境参数，并通过逐跳通信的方式将感知的数据发送给Sink节点。当Sink节点收集和处理其监测范围内的传感节点数据后，通过GPRS、3G等通信方式转发给监控中心。监控中心收集、处理和显示所有传感节点的数据，并提供给用户参考和使用［1］。WSNs通常应用在室内/室外的环境、卫生和健康、电力、库存位置、工厂和过程自动化、地震和结构等方面的监测和动物、人类、车辆等目标的跟踪中［2］，目前已成为热门研究领域，受到政府、学术界和产业界的高度重视。

在无线传感网中，传感节点通常采用电池供电，例如，Crossbow公司的IRIS、MICA等节点都采用两节AA电池供电［3］。一般情况下，传感节点分布在无人看管的环境中，其电池很难更新或充电。经过有限的时间后，传感节点会消耗完自身的能量而失效。但是在无线传感网的应用中，通常要求无线传感网能工作几个月或一年，且不能充电。因此降低节点的能耗，延长网络生存时间是无线传感网的一个重要研究内容。

但是，在周期性收集数据的静态无线传感网(所有节点位置固定不变)中，分布在Sink节点周围的传感节点比其他地方的传感节点消耗更多的能量，且失效较早。这是因为这些传感节点除了发送自身感知的数据外，还较多承担其他传感节点的数据中继任务，因此快速消耗了自身的能量。无论算法怎么调整，这种不均匀的能量消耗都会产生监测区域的能量空穴问题，导致网络的分裂，部分传感节点数据不能达到Sink节点［4-5］。

解决静态无线传感网能量空穴、生存时间优化等问题的一种方法是利用Sink节点的移动，达到优化网络生存时间和平衡节点能量消耗的效果。文献［6］提出范围约束分簇方法RCC(Range Constrained Clustering)，将监测区域内所有节点分成若干个簇。每一个簇节点到簇中心的距离不超过最大通信距离。Sink节点可移动到每一个簇中心收集数据。采用Concorde TSP(travelling Salesman Problem)求解器获得Sink节点的最优移动路径。文献［7］将网络分成若干个网格，提出一种基于网格的分簇方法GBC(Grid-Based Clustering)。在每一个网格内选择一个主簇头，负责与其他网格主簇头通信。选择一个次簇头，负责收集簇内传感节点的数据。Sink节点移动到预先规定的多个网格中心收集数据，没有考虑如何选择Sink节点的移动路径。文献［8］提出了一种基于移动Sink节点的多跳数据采集方案。该算法将监测区域分成若干个圆盘，在每一个圆盘内根据节点的位置分布确定采集点，采用量子遗传算法求解经过所有采集点的最短路线。文献［9］以满足时延要求和最小化网络整体能耗为优化目标，提出了一种基于虚拟点优先级的移动Sink路径优化选择方法。在算法中先根据网格方法划分成若干个虚拟点，优先选择优先级高且移动距离不小于阈值的虚拟点集合，采用TSP算法求解最短路径问题。Sink节点沿着最短路径移动收集多跳通信范围内的传感节点数据。文献［10］将节点的通信范围建模成大小各异且存在重叠的圆盘。在移动过程中Sink节点必须进入所有圆盘。根据不相交环路的特性构造一条赛道，通过内圈启发式、弯道启发式和捷径搜索式寻找赛道内近似最短路径，但是没有考虑Sink节点移动时如何收集数据。

文献［6-10］都没有考虑网络生存时间，只是提出Sink节点移动的路径选择算法，其移动路径是否达到具有最优网络生存时间的Sink节点移动方案，缺乏理论分析和推导。针对上述存在的问题，在总结相关文献的基础上，采用从最优化方法，考虑数据单跳传输的无线传感网，提出优化网络生存时间的Sink节点移动路径选择算法MPSA(Mobile Path Selection Algorithm of Sink Node for Optimizing Network Lifetime)。在MPSA算法中，提出权衡网络生存时间和Sink节点移动路程的优化模型。建立适应度函数，采用改进的遗传算法用于求解优化模型，获得优化网络生存时间的Sink节点移动方案。

1 优化模型的建立

1.1 模型假设

在MPSA算法中，假设［11］:①仅考虑2维无线传感网，即所有传感节点随机分布在2维监测区域中。传感节点位置固定不变，但是Sink节点可移动到监测区域内任一网格的中心位置上收集数据;②由于可采用分簇算法将停留位置分配给不同Sink节点，多Sink节点移动的路程选择问题可转换成若干个单一Sink节点移动的路程选择问题。因此在MPSA算法中，仅考虑单一Sink节点的移动。而且只考虑Sink节点在某个位置上停留一定时间的数据收集，不考虑Sink节点移动过程中的数据收集;③当传感节点不能与Sink节点通信时，即不在其单跳最大通信范围内，所有传感节点的感知数据保存在缓存中，并基本处于睡眠状态。当传感节点能与Sink节点通信，即在其单跳最大通信范围内，传感节点处于工作状态，通过逐跳通信的方式将数据发送给Sink节点;④Sink节点能量不受限制，但是每个传感节点的能量有限且不能补充;⑤所有节点可安装GPS模块或采用其他定位方法获知自身的位置坐标;⑥所有传感节点具有相同的性能(如感应速率、最大通信半径、初始能量、能耗参数等)，采用统一的能耗模型。

1.2 优化模型

由于根据传感节点的位置分布直接确定Sink节点的最优移动位置坐标还存在非常大的困难。因此，将监测区域分成n×n个大小一致的网格，对所有网格从左到右且从上到下的原则进行统一的编码(如图1所示)。Sink节点可移动到任一网络中心上收集数据。令Vg表示所有网格中心集合，xn是Sink节点停留位置的状态指示符号。xn=1表示Sink节点移动到网格中心n上停留一段时间收集数据，即网格中心n在Sink节点的移动路径上。xn= 0表示Sink节点不停留在网格中心n上收集数据。Sink节点需要停留的位置数量是

其中，Nm表示网络中Sink停留位置的数量。

图1 网格分配和编号图

如图2所示，Sink节点的数据收集就是当Sink节点停留在某一个位置(图中五角星表示)上时，静态收集其单跳最大通信范围内的传感节点数据。定义Sink节点从初始位置开始，沿着某一路径收集数据，最后返回初始位置所需要的时间为一个数据收集周期。则Sink节点的一个数据收集周期tc由Sink节点的停留时间和移动时间两部分组成，可表示为

式中，tv

coll表示Sink节点在停留位置v上的停留时间。Vm表示所有停留位置集合，dTSP表示Sink节点移动遍历所有停留位置需要移动的最短路程(假设已知Sink节点的停留位置，则可以通过经典TSP算法求解)，u表示Sink节点的移动速度。

图2Sink节点的数据收集

为保证Sink节点数据收集的全节点覆盖，在Sink节点的数据收集中，要求每一个传感节点至少在一个停留位置的单跳最大通信范围内，即需要满足如下公式:

其中，di，v表示传感节点i到停留位置v的距离，dmax表示节点单跳最大通信距离，Vs表示所有传感节点的集合。

当Sink节点停留在某一个位置，广播通知周围单跳最大通信范围内的所有传感节点。这些传感节点将数据发送给Sink节点。在单跳传输网络中，网络通信协议简单。传感节点只有在Sink节点的单跳最大通信范围内，才将数据发送给Sink节点。因此传感节点的能耗主要由节点数据发送能耗组成［11-12］。在一个数据收集周期间，节点i的数据发送能耗为

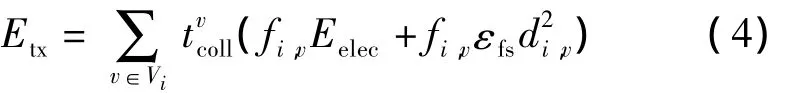
其中，Eelec表示发送1 bit数据时的电路电子能耗，εfs表示放大1 bit数据时的信号放大器电子能耗，fi，v表示当Sink在停留位置v时，传感节点i的数据发送速率。di，v表示传感节点i到停留位置v的距离。Vi表示到传感节点i的距离小于单跳最大通信范围的所有停留位置集合。

定义网络生存时间Tnet是网络开始运行到任意一个节点能量耗尽时所有传感节点给Sink节点发送数据的累计工作时间的最小值(不包括睡眠时间)。假设Sink节点在每一个停留位置上停留时间相同，则该节点i的生存时间为

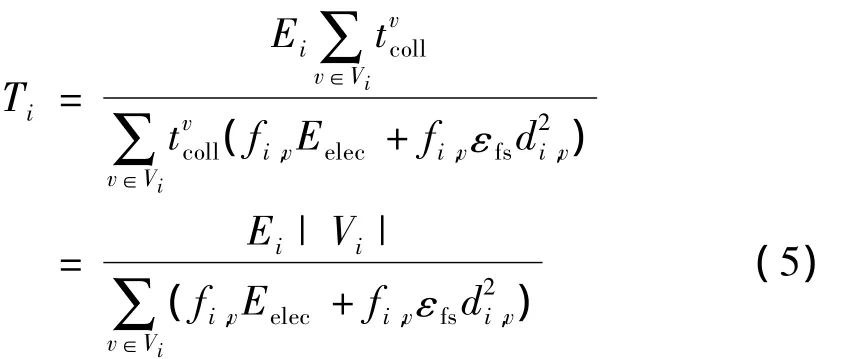
其中，Ei表示传感节点i的初始能量，|Vi|表示集合Vi中元素的个数。

根据上述分析，网络生存时间的优化模型可表示为:

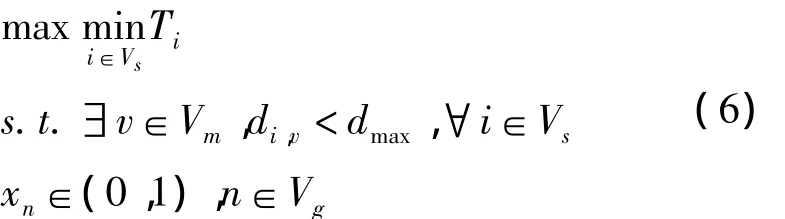
在优化模型(6)的求解过程中，如果不对Sink节点的移动路径进行限制，则求解的移动路径是Sink节点移动到每一个传感节点附近的网格中心收集数据。该方案虽然减低了节点的数据传输能耗，但是大大提高了数据收集周期内Sink节点的移动路程和移动时间，提高了数据传输时延。传感节点的缓存资源有限，如果数据传输时延较高，则部分传感节点缓存空间溢出，一些采集数据不能达到Sink节点，被直接丢弃。因此引入Sink节点的移动路程，将优化模型(6)修改为:

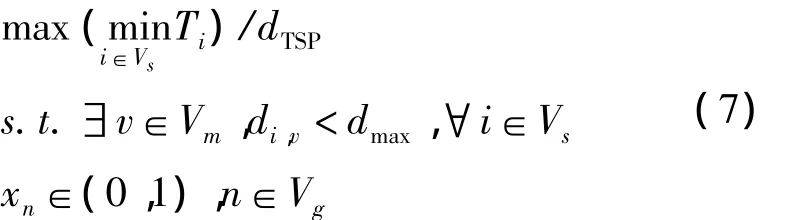
2 模型的求解

如图3所示，本算法采用保证节点全节点覆盖的遗传算法求解优化模型(7)［13］，迭代执行染色体评估、选择、交叉、变异、最小覆盖处理、孤立节点处理等步骤，最终获得优化网络生存时间的Sink节点移动方案。

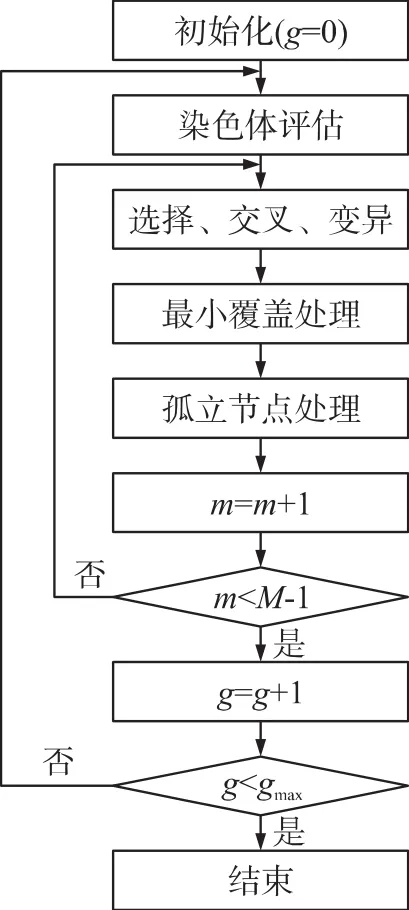
图3MPSA算法流程图

令包括Sink节点停留位置的所有状态指示符号的向量x=(x1，x2，…，xn2)表示染色体，M表示染色体数量，α1表示交叉概率，α2表示染色体发生变异概率，α3表示基因发生变异概率，g表示迭代次数。根据优化模型(7)，遗传算法的适应度函数为

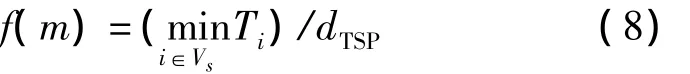
根据适应度函数，采用以下步骤求解优化模型(7)。

步骤1:初始化

初始化全节点覆盖的M个染色体，迭代次数g=0，染色体操作数m=0，算法中α1，α2，α3等参数。

步骤2:染色体评估

计算所有染色体的适应度，直接选择适应度最大的染色体继承到下一代种群中。

步骤3:选择和交叉

根据轮盘赌策略选择需要交叉的2个染色体。令

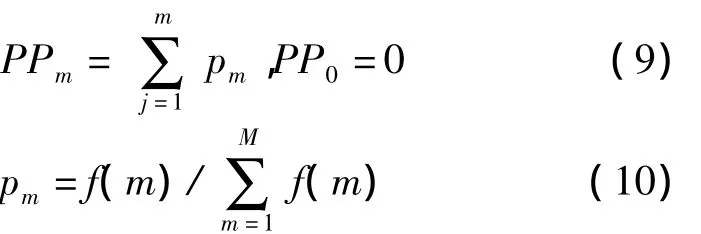
其中，PPm表示累计概率，pm表示个体选择概率。随机选择0到1之间的2个随机数r1，r2。如果PPi-1≤r1＜PPi，PPj-1≤r2＜PPj，则选择染色体i，j。

对染色体i，j进行交叉，生成一个新的染色体k。令gk，l表示染色体k中的基因l，如式(11)所示，所有基因的选择方法如下:产生一个0到1之间随机数q，如果大于α1，则选择染色体j中对应基因，否则选择染色体i中对应基因。

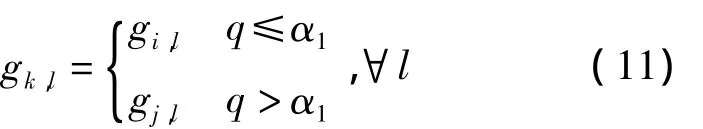
经过n2次基因交叉后，形成了一个新的染色体k。

步骤4:变异

产生一个0到1之间的随机数，如果大于α2，则跳到步骤5，否则需要对新产生的染色体k执行变异操作。如式(12)所示，产生一个0～1之间随机数q，如果q大于α3，则gk，l不变化，否则改变gk，l值，即0变1，1变0。

其中，abs()表示取绝对值函数。

步骤5:最小覆盖处理

根据染色体的所有基因值，获得停留位置集合。计算每一个传感节点到停留位置集合中每一个停留位置的距离。如果该传感节点的最小距离小于dmax，则表示该传感节点能与Sink节点通信。否则，该传感节点为孤立节点。如果某一个停留位置的单跳最大通信范围内没有传感节点，则该停留位置是冗余的，将染色体中对应基因值变成0。

步骤6:孤立节点处理

如果网络中存在孤立节点，则需要添加停留位置消除孤立节点。为控制停留位置的增加数量，选择单跳最大通信范围内孤立节点数量最多且距离平均值最小的网格中心为Sink节点的停留位置。经过多次网格中心的选择，直到该染色体达到全节点覆盖的要求。

步骤7:返回或结束

m=m+1。如果m＜M-1，则跳到步骤3，否则g=g+1且m=0。如果迭代次数g小于gmax，则返回执行步骤2，否则结束遗传算法，获得适应度值最大的染色体，即优化网络生存时间的Sink节点移动方案。

3 仿真实现和分析

3.1 仿真参数设置

在算法仿真中，仅仅考虑数据通信的能耗，不考虑其他的能耗。为方便比较算法性能，假设所有算法的数据收集周期为一个固定值。如表1所示，选择表中参数，在MATLAB软件上编程实现MPSA和RCC算法，分析相关参数对MPSA算法的影响，并比较RCC和MPSA算法。

表1 仿真参数表

3.2 算法关键参数分析

分析网格数量对MPSA算法的影响。分别选择10×10、20×20、30×30和40×40个网格，选择节点数量100、染色体数量30和表1中参数，随机产生10个不同拓扑结构的无线传感网，分别采用改进的遗传算法计算每一种拓扑结构的最优染色体的适应度，获得每一个固定网格数量的最优染色体适应度的最大值、平均值和最小值。如图4所示，当网格数量为30×30时，其最优染色体适应度的最大值(矩形上面的T表示)、平均值(矩形中的红线表示)和最小值(矩形下面的T表示)都比其他网格数量要高。这是因为:当网格数量小于30×30时，随着网格数量的增加，Sink节点的位置选择范围变大，在有限的迭代次数内，算法可以找到较优的移动路径，因此其最大值和平均值变大。但是当网格数量为40×40时，即染色体具有1 600个元素，采用100次的迭代次数还无法找到较优方案，因此其仿真结果值偏低。随着网格数量的增加，染色体的元素数量也增加，且需要更多的迭代次数，这都大大增加了算法的计算量，但是所获得的最优染色体适应度值相差不大。因此为降低算法的计算量，在MPSA算法中，选择网格数量10×10。

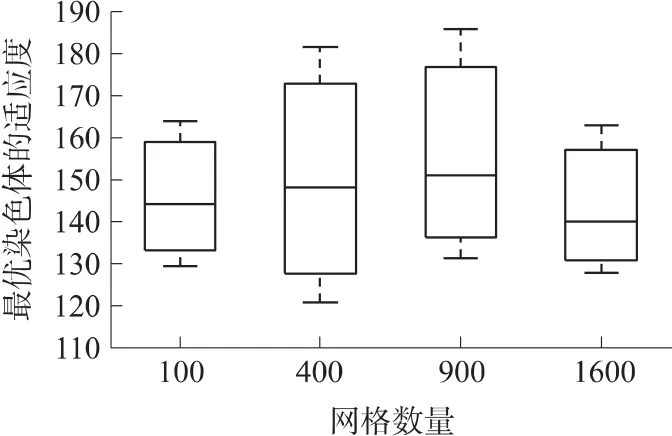
图4 网格数量对最优染色体适应度的影响

分析染色体数量对MPSA算法的影响。分别选择10、20、30和40个染色体，选择网格数量10×10，节点数量100和表1中参数，获得染色体数量对最优染色体适应度的影响图5。如图5所示，随着染色体数量的增加，最优染色体适应度的平均值也随之增加。当染色体数量为30和40时，两者的平均值相差不大。这是因为:当染色体数量小于30时，由于参与计算的染色体较少，在有限的迭代次数中，MPSA算法还没有寻找到较优方案，需要更多的迭代次数。当染色体数量为30和40时，有较多的染色体参与移动路径的迭代计算中，在有限的迭代次数中获得的较优方案，因此两者平均值相差不大。但是由于染色体数量过大，会增加算法的计算量，因此在MPSA算法中，选择染色体个数30。

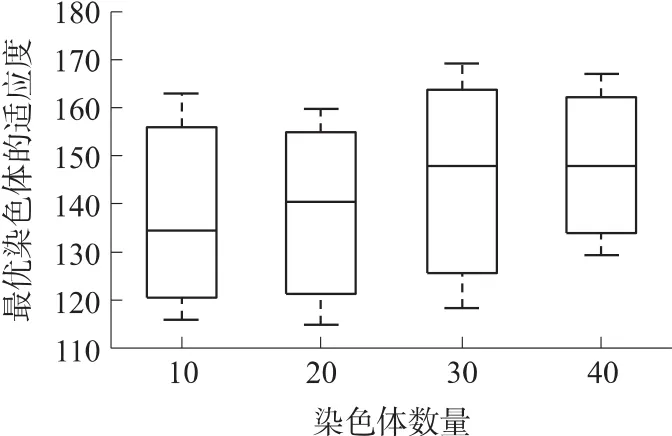
图5 染色体数量对最优染色体适应度的影响

3.3 算法仿真结果分析

为了验证算法的有效性，比较RCC和MPSA算法。根据3.2节的关键参数研究，选择节点数量100，网格数量10×10，染色体数量30和表1中参数，获得RCC和MPSA算法的数据收集图。如图6所示，RCC算法在每一次分簇时，选择在单跳最大通信范围内能覆盖最多传感节点的区域中心作为簇中心，因此Sink节点的停留位置数量只有9个，但是节点的数据传输能耗较大。如图7所示，MPSA算法虽然选择了15个停留位置，但是每一个停留位置到其单跳最大通信范围内传感节点的平均距离较短，降低了节点的数据传输能耗。由于MPSA算法停留位置间距较短而RCC算法的停留位置间距较长，所以两者的移动路程相差不大。

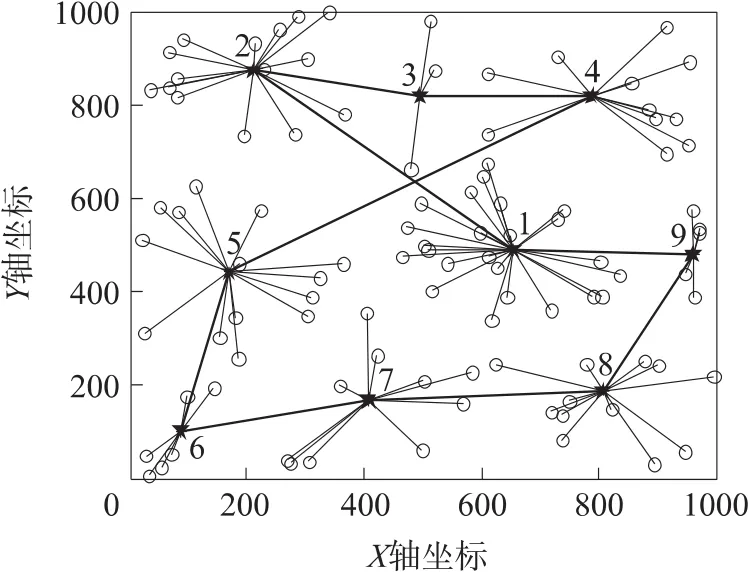
图6RCC算法的数据收集图

图7MPSA算法的数据收集图

在仿真区域内随机均匀分布20、40、60、80、100、120、140、160、180和200个传感节点。选择网格数量10×10，染色体数量30和表1中仿真参数，针对每一种传感节点数量，随机产生10个不同网络拓扑结构，分别计算RCC和MPSA算法的网络生存时间和移动路程，最后取其平均值作为某一传感节点数量的各算法仿真比较值。

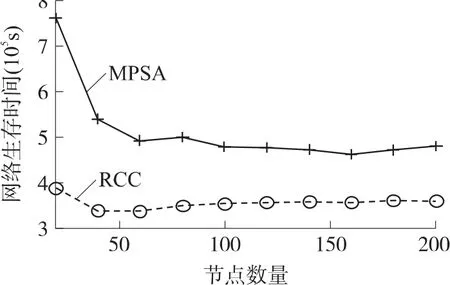
图8 网络生存时间比较图

如图8所示，MPSA算法的网络生存时间比RCC算法高，而且随着传感节点数量降低，MPSA算法提高网络生存时间的效果越明显。这是因为MPSA算法全面考虑监测区域内各个位置，在路径选择时以网络生存时间作为一个主要考虑指标，建立优化模型。在遗传算法求解中优先继承较好网络生存时间的移动路径，经过多次迭代最终获得较优路径。而RCC算法没有考虑网络生存时间，因此MPSA算法能提高网络生存时间。

如图9所示，当节点数量小于100时，MPSA算法的移动路程比RCC算法的移动路程略大，反之RCC算法的移动路程比MPSA算法的移动路程略大，且两者的移动路程都较小。这是因为MPSA算法在染色体的适应度函数中加入了Sink节点的移动路程。在提高网络生存时间的同时尽可能降低Sink节点的移动路程。在其所获的Sink节点移动路径中，虽然停留位置数量增加了，但是停留位置间距较短，而RCC算法的停留位置间距较长，因此MPSA和RCC算法的移动路程上下波动，相差不大。

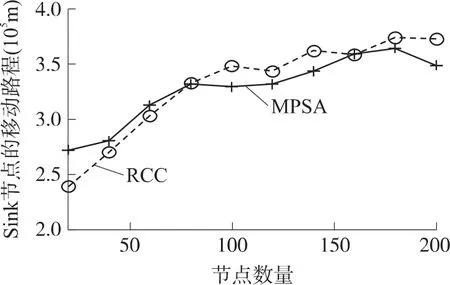
图9 移动路程比较图

综上所述，与RCC算法相比，MPSA算法能明显提高网络生存时间，将移动路程保持在较小范围内。

4 总结

本文研究优化网络生存时间的Sink节点移动路径选择算法(MPSA)。首先提出系统假设，其次从优化模型建立和模型求解二个方面研究MPSA算法。建立权衡网络生存时间和Sink节点移动路程的优化模型。采用改进遗传算法用于求解优化模型，获得优化网络生存时间的Sink节点移动方案。最后仿真分析关键参数对MPSA算法性能的影响，仿真比较RCC和MPSA算法的网络生存时间和Sink节点的移动路程。

MPSA算法是集中式算法。随着节点数量、网格数量等关键参数的增大，算法的计算量也增加，需要较多的迭代时间才能收敛。因此下一步将研究分布式优化算法:每一个节点根据局部信息建立和求解节点优化模型，Sink节点根据周围节点优化模型的解判断下一次的移动位置。

［1］Yang Y，Fonoage M I，Cardei M.Improving Network Lifetime withMobile Wireless Sensor Networks［J］.Computer Communications，2010，33(4):409-419.

［2］Yick J，Mukherjee B，Ghosal D.Wireless Sensor Network Survey［J］.Computer Networks，2008，52(12):2292-2330.

［3］Crossbow公司节点.http://www.memsic.com/wireless-sensor -networks/.

［4］Rao J，Biswas S.Data Harvesting in Sensor Networks Using Mobile Sinks［J］.IEEE Wireless Communications，2008，15(6):63-70.

［5］霍梅梅，郑增威，周晓伟.移动传感器网络及其路由协议研究进展［J］.计算机应用研究，2009，26(11):4010-401.

［6］Kumar A K，Sivalingam K M，Kumar A.On Reducing Delay in Mobile Data Collection Based Wireless Sensor Networks［J］.Wireless Network.2013，19(3):285-299.

［7］Thanigaivelu K，Murugan K.Grid-Based Clustering with Predefined Path Mobility for Mobile Sink Data Collection to Extend Network Lifetime in Wireless Sensor Networks［J］.IEEE Technical Review，2012，29(2):133-147.

［8］郭剑，孙力娟，许文君，等.基于移动Sink的无线传感器网络数据采集方案［J］.通信学报，2012，33(9):176-184.

［9］郜帅，张宏科.时延受限传感器网络移动Sink路径选择方法研究［J］.电子学报，2011，39(4):742-747.

［10］袁远，彭宇行，李姗姗，等.高效的移动Sink路由问题的启发式算法［J］.通信学报，2011，32(10):107-117.

［11］陈友荣，王章权，程菊花，等.基于最短路径树的优化生存时间路由算法［J］.传感技术学报，2012，25(3):406-412.

［12］汪林云，刘文军.无线传感器网络中带有移动汇点的能量高效的数据收集协议［J］.传感技术学报，2012，25(5):678-682.

［13］Luo X N.Hybrid Genetic Algorithm Using a Forward Encoding Scheme for Lifetime Maximization of Wireless Sensor Networks［J］.IEEE Transactions on Evolutionary Computation，2010，14 (5):766-781.

王章权(1969-)，男，硕士，浙江诸暨人，副教授，浙江树人大学信息科技学院，主要研究方向为无线传感网、控制技术;

陈友荣(1982-)，男，博士，浙江苍南人，讲师，浙江树人大学信息科技学院，主要研究方向为无线传感网、物联网。

优化网络生存时间的Sink节点移动路径选择算法*

王章权，陈友荣*，尉理哲，任条娟
(浙江树人大学信息科技学院，杭州310015)

为克服无线传感网的能量空穴问题，采用最优化方法，研究一种优化网络生存时间的Sink节点移动路径选择算法(MPSA)。在MPSA算法中，将单跳传输的无线传感网监测区域分成多个大小一致的网格，Sink节点可移动到任一网格中心，停留收集单跳最大通信范围内的传感节点数据。分析停留位置的全节点覆盖条件和所有传感节点的能耗，建立权衡网络生存时间和Sink节点移动路程的优化模型。提出一种改进的遗传算法，用于求解优化模型，即迭代执行染色体评估、选择、交叉、变异、最小覆盖处理、孤立节点处理等步骤，最终获得优化网络生存时间的Sink节点移动方案。仿真结果表明:MPSA算法能提高网络生存时间，将移动路程保持在较小范围。在提高网络生存时间方面，比RCC算法更优。

无线传感网;网络生存时间;路径选择;优化算法

TP393

A

1004－1699(2014)03－0409－07

2013-12-13修改日期:2014-03-08

C:6150P

10.3969/j.issn.1004－1699.2014.03.025

项目来源:浙江省自然科学基金项目(Y13F010013，Q12F03014);浙江省教育厅项目(Y201330053)