Abnormal Series Detection Based on Trend Analysis with Point Compression*

LI Bin，LIU Ruiqin，LIU Xuejun

(College of Electronic and Information Engineering，Nanjing University of Technology，Nanjing 210009，China)

Abnormal Series Detection Based on Trend Analysis with Point Compression*

LI Bin，LIU Ruiqin*，LIU Xuejun

(College of Electronic and Information Engineering，Nanjing University of Technology，Nanjing 210009，China)

As a special mode of time series，abnormal sequence plays a very important role.But most time series use the distance-based method in similarity measure，ignore the morphological feature of time series itself.Therefore，this paper proposes an abnormal series detection algorithm based on trend contrast，makes use of the bottom-up linear approximation method with combination of important point and the piecewise linearization.And to extract trend features with higher accuracy，the paper fuses the adjacent subsection on the premise of minimizing the two new optimal object function.Moreover，for the purpose of reducing the complexity of the algorithm，time series were collected after deleting redundant point by Douglas-Peucker algorithm，which keeps the whole trend feature of the sequence and to some extent reduces the amount of calculations.The results of simulation demonstrate that the detection algorithm is feasible，and it not only improves the detection accuracy，but also enhances the sequence visualization of the change in trend.

sensor network;time series;outlier data;trend feature;piecewise linear approximation;subsection integration EEACC:7230

时间序列最早被应用于经济预测，是指将某种现象某一个统计指标在不同时间上的各个数值按时间先后的顺序排列而形成的序列，这些值可以是具体的实数值，也可以是特定模式的数值或者是观察事件发生的数目。随着科学技术的迅速发展，对于信息的获取和分析等处理基本转换成对数据的处理，而大多的数据都是以时间序列的形式提供，尤其是在动态数据的监测环境中(比对单个数据的检测更有意义)，如传感器网络，全球定位系统，卫星导航等。因此，时间序列作为各领域研究的热点，对于动态系统中的知识获取［1］、控制决策等具有重要意义，并在科学、商业和工业等领域有着广泛的应用前景。通常情况下，异常时间序列数据在序列的挖掘过程中有着不可或缺的地位，因为这些数据往往代表着某种异常事件的发生，例如通过对股市、证券交易等异常序列数据的分析来预知未来的走势，或是在某些监测系统的传感器中，通过感知的异常序列能够对火灾、飓风［2］或入侵有较好的监测和提前预警作用。而趋势作为时间序列模式挖掘领域里的一个重要特征，更能反映出时间序列变化的重要信息，因此在时间序列数据库里利用趋势的变化来描述序列是发现相似序列、相关联模式或离群序列最直观的方法。

时间序列趋势的挖掘，可以看作是对序列移动方向一种高层模式的挖掘。由于趋势可以较直观地用稳定上升、稳定下降或者周期波动等日常用语表示，因此这种直观的长期趋势是现象运动和发展变化的基本态势，这种态势不仅存在于过去，而且还可能延伸到未来。对时间序列长期趋势的研究，可以帮助人们对现象的前景和将来的状况进行预测，并且通过这些从时间序列分离出来的趋势还有助于更好地观察各种序列季节性变动、循环变动和不规则变动，尤其是在股票市场预测分析、环境趋势分析或金融证券分析等应用中。所以，本文提出了一种时间序列趋势的挖掘算法，通过序列的趋势变化情况来挖掘出异常时间序列，并且利用冗余点压缩算法较好地解决了时间序列数据量带来的计算复杂度问题。

本文后续内容安排如下:第2节介绍了当前相关的研究工作;第3节提出了一种基于冗余点压缩的趋势异常时间序列挖掘算法;第4节通过仿真实验分析了该算法的性能，进一步验证了该方法的有效性;第5节在总结全文的同时提出了更深层次的研究工作。

1 相关研究

随着时代的进步和各领域的需求，时间序列被广泛扩展到军事科学、空间科学、气象预报和工业自动化等部门。而异常序列的检索以大规模时间序列数据库相似查询(搜索)为基础，成为近年来数据挖掘的热点内容之一。异常(离群)序列，采用Hawkin的定义［3］可理解为在传感器采集到的序列中那些偏离大部分正常时间序列的序列，使人怀疑其是由不同的机制产生的而非随机偏差造成。在之前的研究中，绝大多数研究集中在时间序列中存在的异常点或序列数据的相似性模式，且这些算法普遍采用基于密度或距离的度量方式，需要各点数据的一一对应或等同。而在实际生活中，会有以下两种情况: (1)每个数据点并不是十分的重合，或者说整体数据在被采集时会因为周围环境的影响使整个数据的具体值偏高或偏低，但是时间序列的整体变化趋势却是较为正常;(2)被检测序列与正常序列出现交叉现象或距离很近，但是变化趋势却截然不同，若是通过基于距离［3-4，14］的方式进行序列间的相似性度量，则即使距离累计和阈值定义得很小，异常序列也会被误判为正常的。这些都忽视了时间序列在研究过程中的形态特征，导致整体形态在进行比对时造成偏差。一个具体例子如图1所示。

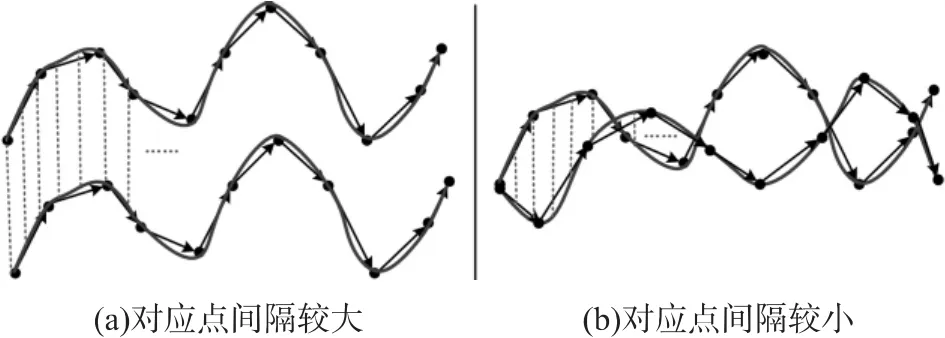
图1 距离表示时间序列特征存在的问题

由图1(a)和1(b)可知，若利用距离累积和计算，由于监测到的值相差过大或过小，会导致最后的距离(不管是点对点距离还是动态时间弯曲距离)累计和偏大或偏小，使得最终的结果判断错误。但是从序列本身的长期趋势分析来看，不难发现图1(a)的时间序列模式的变化信息是正常的，而图1(b)则是相反的结果。因此，Wijsen J［5］提出了趋势依赖的概念，并被广泛运用到气候的季节性变化、股票市场等多领域。虽然利用趋势特征能对时间序列的形态有一个很好的描述，能较准确的进行序列间相似性度量，但对于该特征的提取需要较大的计算量，这也是该算法的局限性所在。为了解决这个问题，在一定程度上对数据进行压缩，Camerra A［6］等提出了一种基于PAA(Piecewise Aggregate Approximation)的数据压缩降维方法，该方法利用各分段的均值来表示序列在各段的特征，虽然达到了高压缩率的效果，但对原序列的整体形态趋势变化没有进行很好的描述。Keogh E［7］等提出了一种子序列匹配算法，该算法首先将监测到的时间序列符号化，通过符号检索出时间序列中最不寻常(异常)的子序列。Dang-Hoan Tran［8］等人利用DFT方法将时间序列转变成频域序列进行离群数据检测，但DFT方法平滑了原序列中局部极大值和极小值，导致许多重要信息的丢失，且该种方法对非平稳序列也不适用。韩敏等［9］提出了一种改进的正交奇异值分解方法EOF-SVD，通过对原始数据进行自然正交分解及奇异值分解，根据得到的变量相关关系对时间序列预测，但其计算量相当大，而且数据动态变化后需要重新计算，这对在线实时数据很不适用。李晓光等［10］提出了一种基于增量PLA的窗口数据近似表示方法，通过动态生成大尺度窗口来适应可变长的趋势变化检测。张力生等［11］则提出了一种基于时间序列重要点分割的异常子序列检测算法，从一定程度上弥补了点异常检测的局限性。

与以上的研究不同，本文提出了一种在冗余点压缩后基于趋势对比的异常序列检测算法。该算法先将采集到的时间序列进行基于Douglas-Peucker算法的逐点压缩，去除冗余点的同时保持了时间序列原有的形态，从而达到一定的检测提速效果。然后，将压缩后的序列进行重要点和分段相结合的自底向上的趋势特征提取，利用数据的分段线性逼近拟合得到各准确分段的斜率，继而转化成趋势。最后将分析的趋势结果与正常序列趋势进行比对，从而搜索出异常序列。该种方法不仅提高了检测精度，还从一定程度上减少了计算复杂度。

2 相关定义与算法描述

2.1 Douglas-Peucker法概述

Douglas-Peucker算法一般用在GIS、计算机制图和计算机图形学等领域，主要是为了实现矢量数据的压缩，它是在经典的垂距法的基础上做了一些改进。如图2所示，其中图2(a)是起伏较大的时间序列经过两种算法处理后的结果示意图，图2(b)表示弯曲度较小的序列经过处理后的结果对比。由图可知，DP不管在何种情况下都能够很好的描述出整条序列的形态，这是因为道格拉斯-普克算法可准确的删除小弯曲上的定点，能从整体上有效地保持线要素的弯曲形态特征，而垂距法却只考虑了线的局部，每次处理时，当时间序列各相邻点起伏变化不大时，在处理过程中可能删除掉所有的中间点，造成形态的严重失真。

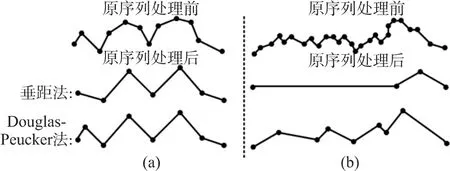
图2 两算法处理结果对比

为了能更好地理解本文采用的数据压缩方法，简单介绍Douglas-Peucker法的基本思想。即对分段后的每条时间序列的首尾两点虚连一条直线，求出序列上所有的点到该条虚连直线的距离，同时找出这些垂线距离值中的最大值Dmax，定义一个垂线段的最大距离阈值D，用Dmax与D进行比较:(1)若Dmax＜D，则将序列上这两点间全部的中间点删去; (2)若Dmax≥D，则保留Dmax对应的坐标点，并以该点为界，把曲线分成两部分，以此类推重复使用该方法，直到处理完全部的序列为止。该算法的示意图如下图3所示。

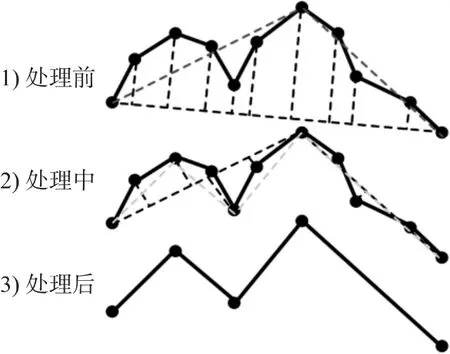
图3 具体DP处理过程示意图

2.2 基于DP的时间序列冗余点压缩

时间序列的相似性搜索是时间序列数据挖掘的基础问题，而相似性度量的定义和搜索算法的时间复杂度一直以来是它的瓶颈。在实际应用中，对于采集到的数据流时间序列，若不作任何处理直接对这些数据进行序列检测，其算法的计算复杂度是难以想象的，并且很不利于数据的传输。因此，本文采用DP(Douglas-Peucker，道格拉斯-普克)算法对时间序列先进行数据的压缩，减少两序列间的点比对数目，从一定程度上提高检测的速度。

定义1(时间序列)假设采集的时间序列可看作是一系列的观测值和观测时间组成的有序集合，则可表示为:

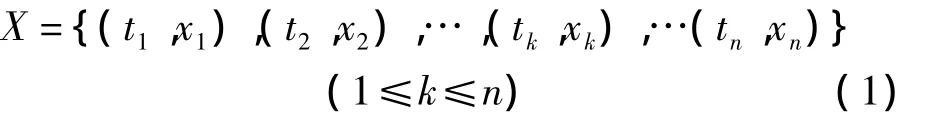
定义2(垂线段的距离)假设序列上数据点A(tA，xA)、B(tB，xB)、C(tC，xC)，其中点A和点B是DP算法中的首尾两点，点C是中间点，则数据点C到AB连线上数据点的距离为:

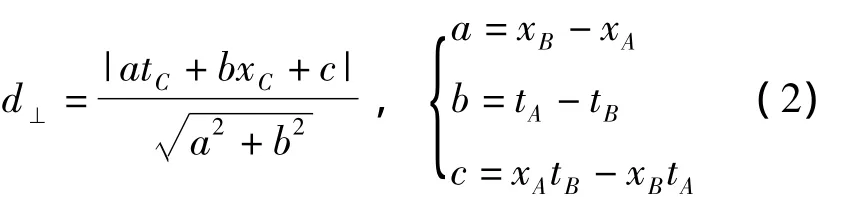
定理1(垂线段距离简化定理)在连续变化的时间序列中，序列上的点如定义2中所描述，则在算法的执行过程中，距离可简化为d'⊥=|atC+bxC+c |，无需再计算d⊥中分母的值。

证明:在时间序列中，由于tA＜tC＜tB，可推知b2=(tB-tA)2＞0，所以d⊥中的分母。在利用DP法计算过程中，只是为了找出首尾两点间d⊥的最大值Dmax，从而能够与限差阈值D进行比较。对于首尾AB两点间所有中间点的d⊥来说，分母的值都是相等的，所以在进行点压缩过程中，可以忽略计算垂线段距离的分母值。

基于Douglas-Peucker法的时间序列的冗余点压缩算法的伪代码可归纳如下:

functionDPFilter(seriesList［］，D)

{//找出最大距离的点及所在位置

Dmax←0，index←0;

//初始化序列的大值和最大值所在的位置

for(i=2;i＜=seriesList.length-1;i++)

{

a←seriesList［end］.y-seriesList［1］.y;

b←seriesList［1］.x-seriesList［end］.x;

c←seriesList［1］.y*seriesList［end］.x

seriesList［end］.y*seriesList［1］.x;

d←abs(a*seriesList［i］.x+b*

seriesList［i］.y+c);//计算改进的垂线距离//找出垂线距离最大的数据点

if(d＞Dmax){index←i;Dmax←d;}

}

if(Dmax＞=D)

{//Dmax超过阈值，则以Dmax所在位置为界，将

//分成前后两部分

//将序列分成的两部分继续回调DPFilter函数，

//直到去除完所有的冗余点为止

frontPart［］←DPFilter(seriesList［1…index］，D);

backPart［］←DPFilter(seriesList［index…end］，D);

resultList［］←{frontPart［1…end-1］

backPart［1…end］};

}

else

resultList［］←{seriesList［1］，seriesList［end］};

return resultList［］;

}

2.3 时间序列的逐段线性化趋势提取

2.3.1 时间序列数据的分段线性表示

虽然在2.2节中利用道氏算法对时间序列进行了数据的压缩并保留了序列的整体形态，但是对于动态变化的时间序列来说，是无法单纯地用直线拟合出来的。所以对基本趋势的提取，必须依次逐段比较斜率，将复杂的曲线简化为有限个直线段来提取线性结构特征。换言之，即将数据压缩后的时间序列先进行一定的分段，再对每个分段内的数据进行最小二乘线性拟合，从而提取出各段的趋势值，这样就可以对每个直线段的形态有一个自然描述，即将连续的斜率值用有限的自然语言概念(上升，下降，平稳)［5］来表示。

趋势变化信息是时间序列的重要特征，在数学领域中，曲线上极值点的两侧基本趋势是完全不同的。本文将这一思想运用到时间序列的自然转折点上，将其作为时间序列分段的自然分割点，并提出重要点的概念。

定义3(序列重要点)对于数据压缩后的时间序列X={(ti，xi)}Ni=1，对于∀xi(i=1，2，…N)，若对任意满足式(3)的xj，都有xi≥xj(xi≤xj)，则称xi为序列的重要点。

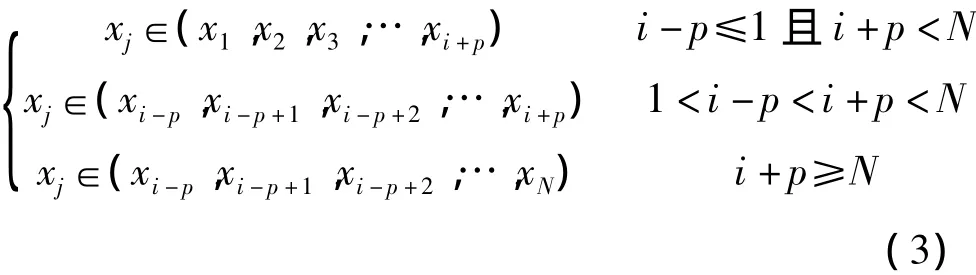
其中，p为给定的一个常数。

重要点分段法是时间序列的一个重要算法，本文将时间序列X={(ti，xi)}={Xj}划分为r段，各分段间互不相交且不含重要点。假设序列的第j分段的起点和终点位置分别为sj、ej，则用线性模型来拟合时间序列在区间［tsj，tej］上的关系为φj(ti)=ajti+bj+E0，其中φj(ti)是响应变量，ti是回归变量，E0为误差项。则利用最小化误差平方和作为目标函数:

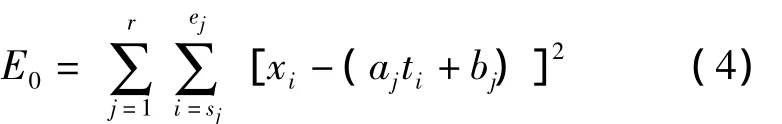
目标函数E0表示了原时间序列与分段线性近似之间的拟合程度，由式(4)可知，E0越小，分段线性近似表示对原时间序列的拟合越好。因此最小化目标函数，可得到较精确的拟合参数，从而可提取较准确的趋势值。

为了便于直观地观测各个分段的趋势变化，对各个分段上的趋势定义如下:

定义4(基本趋势)在第j段时间序列Xj上，对于sj≤i≤ej中点的分段线性近似φj(ti)≈ajti+bj上的基本趋势记为:

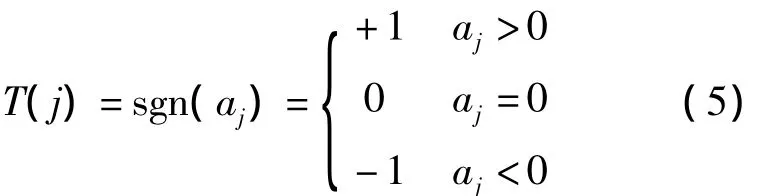
其中，趋势值aj＞0表示上升趋势，aj=0表示平稳趋势，aj＜0表示下降趋势。

时间序列的分段线性近似的最大好处在于可以快速分析时间序列的趋势，而将各趋势进行简单的数字化更便于在离群检测时的比对。

2.3.2 基于逼近原则的趋势特征提取

趋势值的精确提取一直是一个难题，为了最小化目标函数E0，大多数的文章采用改变时间序列分段的数量r、改变各分段区间的长度或改变对每一分段进行线性拟合的方法等。蒋嵘等［12］利用定长分段线性化方法对各分段区间内的数据进行线性拟合来较快地得到相应的线性化模型，但是对于复杂的时间序列来说，不同区间内的时间序列变化也不同，当分段长度相等时，误差比较大，基本趋势也有可能被错误提取。通常情况下，分段数越多，对序列的逼近效果越好，但会使压缩效果变差，这样就背离了本文对快速变化数据流时间序列处理的初衷。所以本文利用自底向上的线性化方法，通过调整各分段时间区间的长度，并在进行分段线性拟合的同时根据分段数和误差平方和的关系，选定具体的分段数。

虽然利用分段线性化的方法，可以获得时间序列在不同精度的抽象表示，但是近似误差为目标函数会使某些显著的趋势在拟合过程中失去原有的特征。为了能更好地进行分段线性近似拟合以及对趋势的准确提取，本文利用式(4)的思想，将每个点的趋势值与每段的趋势值之间的误差作为最小优化目标函数，以此来提取更准确的结果，相关的定义如下:

定义5设时间序列X上的任一个点(ti，xi)，则其在该段序列上的趋势值为:

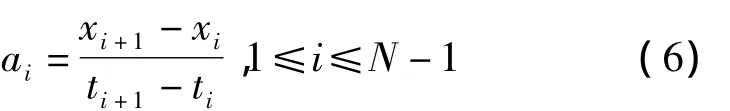
则在分段数r下关于趋势的最小目标函数为:

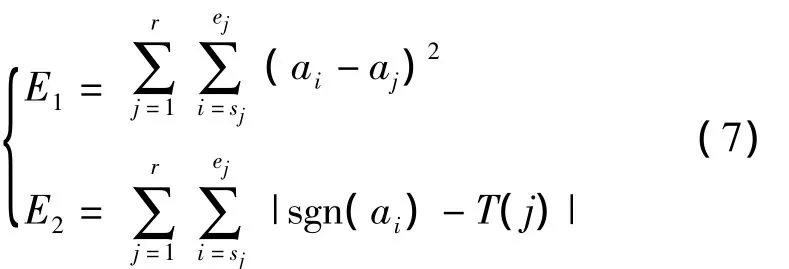
其中，E1表示整个时间序列的趋势值和各分段趋势值之间的误差，E2则表示分段趋势与整体趋势的不一致程度。为了保证基本趋势的正确提取，最小化式(7)中的目标函数，使得分段线性近似得到最优化。显而易见，同时优化E1和E2是很困难的，必须将多目标优化问题进行简化。而本文是为了较准确地提取序列的趋势，即保证趋势基本一致，因此可以将问题转化为在E2=0的条件下最小化E1的单目标问题。

定理2假设在时间序列第j(1≤j≤r)分段(sj，ej)中不包含重要点，若要使第j分段内点的趋势值与原序列趋势值的误差最小，则第j分段线性近似斜率(趋势值)的值为:

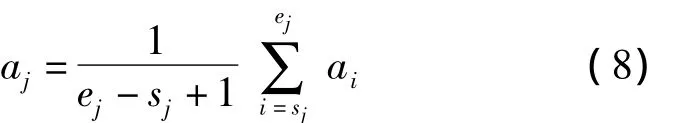
证明:在第j分段(sj，ej)内，各点的趋势值(斜率)为ai∈{asj，asj+1，…，aej-1，aej}，则由式(7)可知，趋势值之间的误差为:

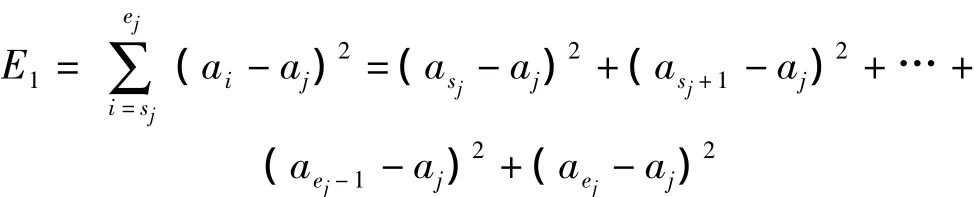
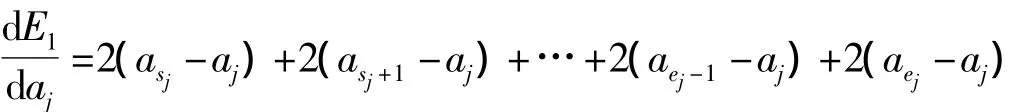
由上述定理2的结果可知，在目标函数E2=0时，可得出因此，不难看出在分段内各点的趋势和段内所有点的整体趋势是一致的，换而言之，即在各个小分段开区间内不存在重要点(分段点)，这样就需要寻找重要点(分段)位置，以达到准确的趋势特征提取。所以本文利用逐段融合的思想，首先将时间序列分为若干个较小的初始分段，同时形成满足相关条件的初始位置，然后逐步合并初始分段，使满足定义5中的目标函数最优化，从而确定新的分段位置，直到没有可融合的分段为止。假设两相邻可融合的分段位置为ξ(第ξ分段和第ξ+1分段为可融合分段)，则融合后趋势值之间的误差以及相关融合段的趋势值为:

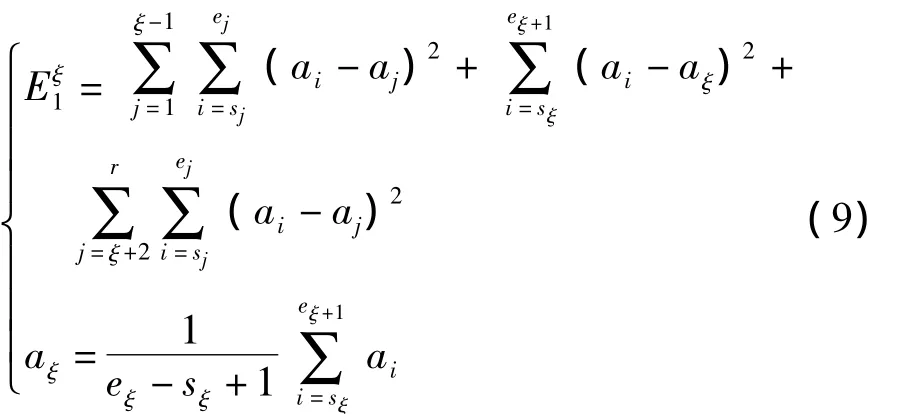
2.4 基于趋势对比的离群序列检测算法(TOTSD)

2.4.1 检测算法的设计模型

对于采集的数据流［13］时间序列，首先进行2.2节的数据预处理，即基于改进的道格拉斯-普克算法的时间序列冗余点压缩，这在一定程度上保持数据序列原有形态特征的同时还较大地减少了数据量。接着在时间序列经过压缩后，进行如2.3节的重要点和分段线性化方法相结合的趋势特征提取，同时对相邻分段进行自底向上的分段融合。其设计模型如图4所示。

图4 算法设计模型

2.4.2 算法描述

输入:采集到的时间序列X={(ti，xi)}ni=1，常数D，p，l，α，ε

输出:不匹配度λ，异常序列标志flag

Step 1对时间序列调用DPFilter(X，D)，获得压缩后的序列X'，并将其标志flag置为0(默认为正常);

Step 2根据定义3提取出X'的重要点位置，同时根据定义5的式(6)求出X'的各点的趋势值ai，并根据定理2的结果，将相邻两个重要点之间的斜率ak作为重要点分段趋势值，记录最后的重要点个数q，其中k∈{1，2，3，…，q};

Step 3将序列按照重要点的位置分成q-1段，根据定义5中式(7)的关于趋势值拟合误差的定义计算出重要点分段的E'1;

Step 4将序列的每个重要点分段再划分为初始长度为l的小分段，当第k重要点分段不能被l整分时:1)若第k重要点分段的长度Nk小于l，则将该段单独作为一个初始小分段;2)若Nk大于或等于l，则将Nk整除l得到各小分段。同时在各重要点分段内计算出初始小分段拟合误差E1;

Step 5若E1＞αE'1，则减小l并转到Step 4;若E1≤αE'1，将相邻分段融合，同时根据式(9)计算融合后的E1=Eξ1，判断:1)若Eξ1≤αE'1，记录融合后的新分段位置，更新分段数，使迭代融合;2)反之，放弃融合。

Step 6求出融合后的总段数r;

Step 7将融合后得到的完整的趋势特征与正常序列特征进行对比，同时记录出不匹配的趋势特征段数m，利用λ=m/r计算出不匹配度，其中，m表示检测的不匹配趋势段数;

Step 8若检测到的当前序列的不匹配度超过阈值，即λ＞ε，则将标志flag设为1(表示该序列为异常序列);反之，若检测到的λ≤ε，则不改变标志，该序列为正常序列。

3 算法实验分析

本文采用MATLAB7.1实现上述所提出的算法，并从拟合度、精确度和计算效率等几个方面进行性能分析，来验证基于趋势对比的离群序列检测算法的有效性。

3.1 不同D-阈值下的性能分析

如图5所示，描述了两条长时间序列在不同压缩阈值D下进行本文所提出算法处理后的运行时间对比，其中DataSet_s和DataSet_f分别表示趋势变化不明显(较平稳)和波动相对较大的两条数据量相同的时间序列。由图5可知，随着阈值的增大，算法所需的运行时间逐渐减少，这是因为阈值越大，在进行DP算法处理后，对中间的冗余点的删除效果就越好，即压缩率越高。但是在较低的压缩阈值下，由于DataSet_f起伏较大，对于很多不影响检测结果的点都保存了下来，相对于序列DataSet_s，在后续进行异常趋势检测时所需的运行时间就相对较大，但是随着阈值的增大，DataSet_f表现出了相对的优势。

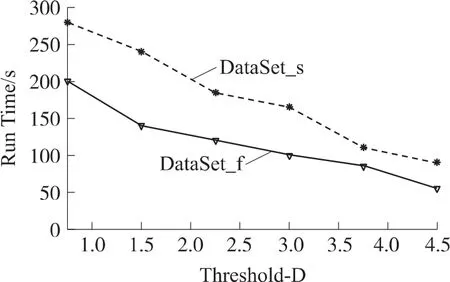
图5D-阈值下的运行时间对比

图6 表示两序列的拟合度(通过压缩后进行趋势比对的不匹配度λ所得)对比，从图中可看出，压缩率越小，对原序列的拟合效果越好。而且随着D的增大，更利于DataSet_f的检测。这是因为波动较大的序列，其形态特征点较为明显，D越大，对于中间的过渡点有很好的删除作用，相对较平稳的序列DataSet_s而言，对采集到的序列的整体形态有更好地描述，从而使得后期的趋势特征提取的误差率相对较小。综合图5和图6中的结果分析，可得出在阈值D为3.0时，算法在精度和时间效率上都有一个较好地把握，更利于时间序列的离群检测。

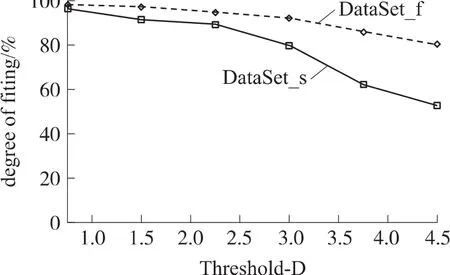
图6D-阈值下的拟合度对比

3.2 精确度(正确率)对比

取阈值D=3，同时使λ＞10%时认为序列偏离正常序列的趋势过大，即判为离群序列。图7显示了3种相似性查询算法在六组不同的时间序列数据训练集下的检测精确度，其中精确度认为是检测到的离群序列的个数与期望得到的离群序列的总数之间的比值。由图可知，PAA算法与DTW［14］和本文所提的TOTSD算法相比较，检测精度是最低的，这是因为PAA算法将采集到的序列按照等长间隔分段，并利用每个分段内点的均值表示该段整体的序列数据值，对于长序列的整体形态不能有一个较好的描述，更体现不出时间序列的发展趋势，这样在进行序列间距离计算时就会有较大的误差，导致最后的离群检测的错误率较高。而经典的DTW算法采用了在距离矩阵中递推式的最短路径搜索方法，弥补了传统的一对一式的距离比较算法的缺陷，解决了序列间出现平移后可部分重合现象的问题，在准确度上有了较大地提高。综观本文所提的TOTSD算法，采用了重要点和分段相结合的自底向上的分段融合的趋势特征提取，在检测精度的把握上与DTW基本保持一致，并在一定程度上针对距离累计计算带来的不足(如时间序列集DataSet4，与正常序列数据值出现交叉和距离拉大现象较多)，发挥出了较大的优势。但是由于先经过了基于DP算法在D阈值下的冗余点删除，导致在某些长时间序列训练集的检测准确率上稍有偏差，可并不影响对序列整体发展趋势的观测效果。

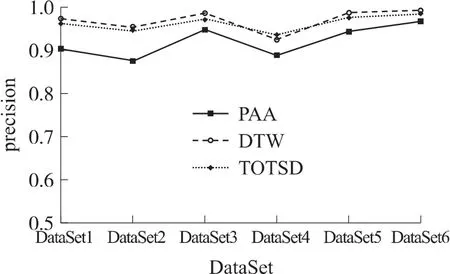
图73 种算法的精确度对比

3.3 计算时间效率

如图8所示，DTW由于采取普遍的动态规划方法来搜索距离矩阵中起始点间的最优路径，达到所需的较高的检测精度，但却是以牺牲计算时间为代价的。而本文所提出的TOTSD算法由于先进行了基于道格拉斯-普克算法的冗余点删除，在整体形态趋势保持不变的基础上对采集到的原序列有较大的压缩处理，虽然没有同样具备压缩效果的PAA算法处理速度快，但是比起DTW算法有了很大的进步，并且在某些时间序列数据训练集上比PAA算法的速度更快(如起伏间相隔时间较长的DataSet2，对数据有着很好的删减效果)。比较该3种算法的整体性能，本文的TOTSD算法较好地兼顾了时间效率和检测精度。

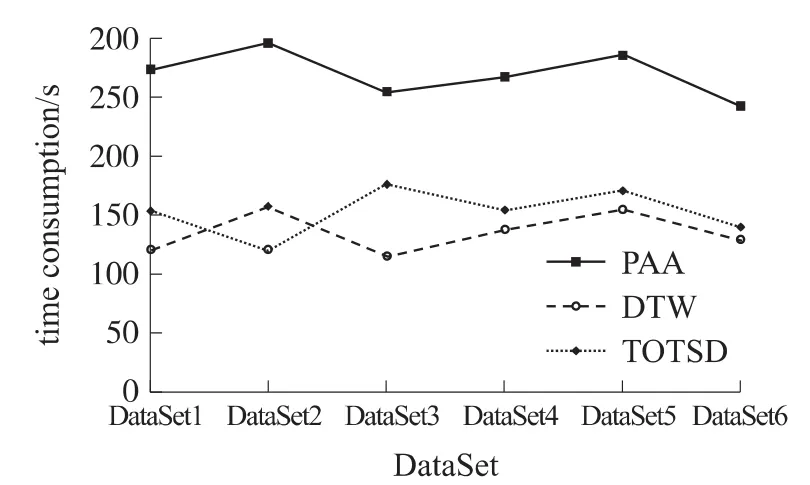
图83 种算法的时间消耗对比

4 总结与展望

本文提出了一种基于趋势特征的异常序列挖掘算法TOTSD，与已有关于趋势特征提取算法不同的是:先利用DP算法对采集到的时间序列进行冗余点的删除，达到数据压缩效果的同时保持了序列的整体形态，更加有助于对长序列数据的后期处理;然后在以重要点分段保证线性基本特征不被错误提取的前提下，以小尺度分段进行自底向上的分段融合，并通过两个新的优化目标函数使融合后的线性拟合误差最小。通过实验验证了TOTSD算法的有效性，既提高了检测的准确度，又在一定程度上减少了计算开销。本文接下来的工作是对算法进行改进，进一步提高它的检测速度，并与实际应用相结合，考虑海量数据的高维和在线检测等问题，提高该算法的实际应用价值。

［1］Keogh E，Kasetty S.On the Need for Time Series Data Mining Benchmarks:A Survey and Empirical Demonstration［C］//Proceedings of the 8th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，Edmonton，Alberta，Canada，2002，102-111.

［2］刘良旭，乐嘉锦，乔少杰，等.基于轨迹点局部异常度的异常点检测算法［J］.计算机学报，2011，34(10):1966-1975.

［3］刘瑞琴，刘学军.WSN中基于加速动态时间弯曲的异常数据流检测［J］.传感技术学报，2013，26(6):887-893.

［4］Rakthanmanon T，Campana B，Mueen A，et al.Searching and Mining Trillions of Time Series Subsequences under Dynamic TimeWarping［C］//18th ACM SIGKDD Int Conf Knowledge Discovery and Data Mining，Beijing，China，2012:262-270.

［5］Wijsen J.Trends in Databases:Reasoning and Mining［J］.IEEE Transactions on Knowledge and Data Engineering，2001，13(3): 426-438.

［6］Alessandro Cammerra，Themis Palpanas，Jin Shieh，et al.iSAX 2.0: Indexing and Mining One Billion Time Series［C］//IEEE International Conference on Data Mining.Washington:IEEE，2010:1 -13.

［7］Keogh E，Lin J.Finding Unusual Medical Time-Series Subsequences: Algorithms and Applications［J］.IEEE Transactions on Information Technology in Biomedicine，2006，10(3):429-439.

［8］Dang-Hoan Tran，Jin Yang.Decentralized Change Detection in Wireless Sensor Network Using DFT-based Synopsis［C］//The 12th IEEE International Conference，2011:226-235.

［9］韩敏，李德才.基于EOF-SVD模型的多远时间序列相关性研究及预测［J］.系统仿真学报，2008，20(7):1669-1673.

［10］李晓光，宋宝燕，张昕.基于滑动多窗口的时间序列流趋势变化检测［J］.电子学报，2010，38(2):321-326.

［11］张力生，杨美洁，雷大江.时间序列重要点分割的异常子序列检测［J］.计算机科学，2012，39(5):183-186.

［12］蒋嵘，李德毅.基于形态表示的时间序列相似性搜索［J］.计算机研究与发展，2000，37(5):601-608.

［13］曼苏尔，于晋龙，马书惠.一种基于数据流跟踪的无线传感网能量模型及网络优化［J］.传感技术学报，2009，22(4):505-510.

［14］Sakurai Y，Faloutsos C，Yamamuro M.Stream Monitoring under the Time Warping Distance.ICDE，2007:1046-1055.

李斌(1979)，男，江苏省南京市，硕士，讲师，主要研究方向包括数据库，传感器网络等;

刘瑞琴(1989)，女，江苏省苏州市，硕士生，主要研究方向为数据挖掘，异常检测，传感器网络，liuruiqin_r@163.com;

刘学军(1971)，男，江苏省南京市，副教授，博士，主要研究方向包括数据库，数据挖掘，传感器网络等。

基于冗余点压缩的趋势异常序列检测*

李斌，刘瑞琴*，刘学军
(南京工业大学电子与信息工程学院，南京210009)

异常序列作为时间序列的一种特殊模式有着极其重要的作用，但大多数的时间序列利用基于距离的方法进行序列间的相似性度量，忽略了时间序列本身的形态特征。为此，提出了一种基于趋势对比的异常序列检测算法，利用重要点和分段线性相结合的自底向上的线性逼近方法，并以最小化两个目标函数为目的进行相邻分段融合，从而使提取的趋势特征有较高的准确度。而且为了降低提取算法的复杂度问题，对采集到的时间序列先进行道格拉斯-普克算法的冗余点删除，保持序列整体形态的同时从一定程度上减少了计算量。最后通过仿真实验，验证了所提出的检测算法的有效性，不仅提高了检测的准确率，还增强了序列趋势变化观测的直观性。

传感器网络;异常序列;离群数据;趋势特征;分段线性逼近;分段融合

TP393

A

1004－1699(2014)03－0401－08

2013-12-16修改日期:2014-02-20

项目来源:国家自然科学基金项目(61073197);江苏省科技支撑计划项目(SBE201077457);国家质检公益性科研专项项目(201210022)

10.3969/j.issn.1004－1699.2014.03.024