基于几乎干扰解耦的非线性系统自适应模糊输出反馈控制
李 长 英, 王 伟
( 大连理工大学 控制科学与工程学院, 辽宁 大连 116024 )
基于几乎干扰解耦的非线性系统自适应模糊输出反馈控制
李 长 英*, 王 伟
( 大连理工大学 控制科学与工程学院, 辽宁 大连 116024 )
研究了一类基于几乎干扰解耦的MIMO非线性不确定系统的输出反馈控制问题.研究的非线性系统具有嵌入式下三角结构,比严格反馈形式的非线性系统更具一般性,非线性系统的状态部分不可测.通过综合应用模糊逻辑系统和命令滤波反推控制技术,构建自适应模糊输出反馈控制器,命令滤波技术的引入消除了传统反推控制方法运算中存在的计算膨胀,设计的控制器不仅保证整个闭环系统的稳定性,而且在L2增益的意义上抑制了干扰对输出的影响.仿真结果表明了该方法的有效性.
非线性系统;自适应模糊控制;命令滤波;几乎干扰解耦;状态观测器
0 引 言
近十几年来,复杂非线性系统的输出跟踪控制和稳定性分析引起了国内外学者的广泛关注,特别是Lyapunov稳定性理论[1]和反推控制技术[2]的综合运用,使MIMO非线性系统的研究取得了令人瞩目的理论成果[3-5].但是所研究的非线性系统多数满足下三角结构,即严格反馈系统.Liu等[6-7]对具有零动态嵌入式下三角结构的非线性系统进行了鲁棒稳定性分析,嵌入式下三角结构的非线性系统更具一般性,包含严格反馈系统,其基于反推自适应控制技术和augmentation 思想的反复运用,给出了嵌入式下三角结构非线性系统鲁棒控制器的设计.
虽然MIMO非线性系统的鲁棒控制[3-5]已经得到了广泛研究,但是由于多变量非线性系统的输入、输出变量的强耦合,以及干扰对输出的影响,MIMO非线性系统的干扰解耦问题更复杂、更难以解决.自从非线性系统的几乎干扰解耦问题首先由Marino等[8]提出并得到基本解决以来,这个问题的研究引起控制界的广泛关注.Liu等[9]对具有嵌入式下三角结构的非线性系统的几乎干扰解耦问题进行了研究,然而,其假设系统模型是精确已知的.在复杂的工业控制过程中,许多被控对象都存在着严重的非线性和不确定性.为了解决这一问题,国内外学者将模糊控制技术与自适应控制相结合,提出了自适应模糊控制方法[10].Chen等[11]针对MIMO嵌入式下三角结构的非线性不确定系统,提出了模糊自适应反推控制方法,控制方案不仅保证了整个闭环系统的稳定性,而且在L2增益的意义上抑制了干扰对输出的影响.但是,多变量非线性系统的反推控制器设计过程中,对虚拟控制的反复求导导致了计算膨胀,文献[12]、[13]分别采用动态平面技术和命令滤波技术,引入虚拟控制的一阶滤波和两阶滤波得到虚拟控制的估计,用积分运算代替微分运算,避免对虚拟控制的反复求导.
上述文献中的控制器设计和稳定性分析均基于系统状态是完全已知的情况下实现的,但是在实际控制工程中,很多系统状态是不可测的.针对MIMO非线性不确定系统的不可测状态,文献[14]设计了模糊观测器,基于Lyapunov函数的方法证明了整个闭环系统的稳定性,但是非线性系统是严格反馈系统且系统中没有考虑干扰解耦问题.
针对以上问题,本文提出基于观测器的模糊自适应命令滤波反推控制方法,用以消除传统反推控制方法引起的计算膨胀,基于Lyapunov函数方法证明整个闭环系统的稳定性,同时在L2增益的意义上抑制干扰对输出的影响.
1 问题描述
考虑下面一类MIMO非线性系统:

xi,ni+1∶=ui,
yi=xi,1;i=1,…,m,j=1,…,ni
(1)

对于系统(1),设计自适应模糊输出反馈控制u,其中u(0,…,0)=0,对于任意的正实数η和π0,存在正定函数V(·)和K∞函数b(·),满足
(2)
由于π0是正实数并且可以选择得任意小,并且对任意的T>0,满足

(3)
故系统(1)的模糊几乎干扰解耦问题得以解决.
控制目标:为MIMO非线性系统(1)设计自适应模糊输出反馈控制器ui(t),保证闭环系统所有信号一致有界,同时在L2增益的意义下抑制干扰对输出的影响.
采用单点模糊化、乘积推理规则及中心加权解模糊化所构成的模糊逻辑系统[10]为
y(x)=θTφ(x)
其中θ∈Rn为参数向量,φ(x)为模糊基函数向量.
引理1[10]f(x)为紧集Ω内连续函数,则∀ε>0存在上述模糊逻辑系统使得

|f(x)-θTφ(x)|≤ε

xi,j)T的光滑函数,故存在模糊逻辑系统逼近光滑的函数fi,j,用模糊逻辑系数去逼近为


(4)
其中θi,j为待设计的自适应参数向量.
定义最优参数向量




系统(1)写成如下矩阵形式:

(5)
其中

(6)
其中βi和λi,m是已知常数.



(7)
假设3存在局部Lipschitz非负常数li,j和μi,s满足

i=1,…,m,j=1,…,ni
(8)


(9)
假设4存在已知常数Hi,j,满足|hi,j(Xi,j)|≤Hi,j,∀i=1,…,m,j=1,…,ni.
假设5ω(t)∈L2[0,t],t∈(0,∞).

2 模糊观测器的设计
针对系统(1),本文设计模糊观测器如下:
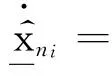

(10)


(11)
其中δi=(δi,1…δi,ni)T.
3 模糊控制器的设计及稳定性分析
下面采用简化的反推控制技术设计自适应模糊输出反馈控制器,限于篇幅,详细推导过程省略.进行如下坐标变换:
;
i=1,…,m,j=2,…,ni
(12)

定义两阶命令滤波方程如下:


(13)
其中ζ和υi,j是设计参数,υi,j是命令滤波的固有频率.









(14)




虚拟控制器设计如下:






(15)
控制律设计如下:

(16)
自适应律的选取如下:
(17)

根据式(1)、(10)和(12),得误差动态方程



(18)
引理2[15]∀ε>0,p>1 和q=(1-p-1)-1>1,对于所有的a∈Rn,b∈Rn,则满足以下不等式

(19)
称式(19)为Young不等式.
定理1基于假设1~5,对系统(1)设计模糊自适应观测器(10),选择控制律(16)和自适应律(17)使得闭环系统满足以下性能:
(1)所有信号一致有界;
(2)干扰到输出的L2增益可以任意小;
(3)选择合适的自适应参数,使得观测误差收敛到零的很小的邻域内.
证明选取Lyapunov函数


(20)
按式(11)~(18)、(20)对V求导数,得


(21)
根据引理2,选取p=2,则

(22)

(23)

(24)
(25)

(26)

(27)

(28)
Si,j(Si,j+1+αi,j)≤|Si,jSi,j+1|+μi,j,1|Si,j|
(29)

(30)
将式(22)~(30)代入式(21),得

(31)
其中



利用Young不等式
(32)
(33)
(34)
(35)
将式(32)~(35)代入式(31),得

(36)


对于给定的常数b,总可以选择合适常数c,使得c>b+1.由式(36)可得
(37)
对任意的T>0,满足

其中


(38)

4 仿真算例
考虑如下一个带有两个连续搅动式水槽反应器的非线性系统[6,11,14]:

(39)
其中






参数取值如下:

假设仅仅系统状态yi(i=1,2,3)是可测的,Φx3,1为前馈项,ω3,1为外部扰动,故系统(39)符合本文研究的系统(1).
控制律和自适应律的设计分别参照式(16)和(17).选取控制律和参数自适应律中的设计参数如下:

初值选取如下:
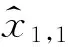
为了更好地证明本文方法对外界干扰的抑制效果,选取不同的外界干扰来讨论:
情况1选取如上的初值和参数,当ω3,2=0.1e-0.15tsint.
情况2选取如上的初值和参数,当ω3,2=0.8sin(0.5t).
图1是系统状态与状态估计曲线图,图2是系统控制输入的曲线图,图3是自适应律向量范数的曲线图.根据系统(39),外界扰动ω3,1的变化对第一个子系统没有影响,由图1~3可知,虽然外界干扰ω3,1的变化影响第二、三个子系统的性能,但是本文的设计方法仍然保证系统状态估计误差、控制输入和自适应律的范数均有界.仿真结果表明,虽然复杂的非线性系统存在不确定性和外界干扰,系统的状态不可测,但是本文设计的模糊自适应输出反馈控制器不仅保证所有信号一致有界,而且在L2增益的意义上抑制了干扰对输出的影响.

(a) x1,1和

(b) x1,2和

(c) x2,1和



(e) x3,1和

(f) x3,2和
图1 系统状态与状态估计曲线
Fig.1 Curves of system state and estimated state

(a) u1

(b) u2

(c) u3
图3 自适应律的2-范数
Fig.3 2-Norm of adaptive law
5 结 语
针对具有嵌入式下三角结构的MIMO非线性不确定系统进行研究,系统更具一般性,并且系统状态部分不可测,此系统的研究更能满足实际控制工程的需求.理论推导和仿真结果证明了基于反推命令滤波技术的自适应模糊输出反馈控制方案的有效性.
[1]Corless M J, Leitmann G. Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems [J]. IEEE Transactions on Automatic Control, 1981,26(5):1139-1144.
[2]Kristic M, Kanellakopoulos I, Kokotovic P V. Nonlinear and Adaptive Control Design [M]. New York:Wiley, 1995.
[3]刘艳军,王 伟,王向东. 一类不确定非线性纯反馈系统的自适应鲁棒模糊控制[J]. 控制与决策, 2007,22(6):697-701.
LIU Yan-jun, WANG Wei, WANG Xiang-dong. Adaptive robust fuzzy control for a class of uncertain nonlinear pure-feedback systems [J]. Control and Decision, 2007,22(6):697-701. (in Chinese)
[4]Lee H. Robust adaptive fuzzy control by backstepping for a class of MIMO nonlinear systems [J]. IEEE Transactions on Fuzzy Systems, 2011,19(2):265-275.
[5]LI Tie-shan, TONG Shao-cheng, FENG Gang. A novel robust adaptive-fuzzy-tracking control for a class of nonlinear multi-input/multi-output systems [J]. IEEE Transactions on Fuzzy Systems, 2010,18(1):150-160.
[6]LIU Xiao-ping, ZHOU Ke-min, GU Guo-xiang. Global stabilization of MIMO minimum-phase nonlinear systems without strict triangular conditions [J]. Systems & Control Letters, 1999,36(5):359-362.
[7]LIU Xiao-ping, GU Guo-xiang, ZHOU Ke-min. Robust stabilization of MIMO nonlinear systems by backstepping [J]. Automatica, 1999,35(5):987-992.
[8]Marino R, Respondek W, van Der Schaft A J. Almost disturbance decoupling for single-input single-output nonlinear systems [J]. IEEE Transactions on Automatic Control, 1989,34(9):1013-1017.
[9]LIU Xiao-ping, Jutan A, Rohani S. Almost disturbance decoupling of MIMO nonlinear systems and application to chemical processes [J]. Automatica, 2004,40(3):465-471.
[10]WANG Li-xin. Adaptive Fuzzy Systems and Control:Design and Stability Analysis [M]. Englewood Cliffs:Prentice-Hall, 1994.
[11]CHEN Bing, TONG Shao-cheng, LIU Xiao-ping. Fuzzy approximate disturbance decoupling of MIMO nonlinear systems by backstepping approach [J]. Fuzzy Sets and Systems, 2007,158(10):1097-1125.
[12]LI Tie-shan, LI Wei, LUO Wei-lin. DSC approach to robust adaptive NN tracking control for a class of MIMO systems [J]. International Journal of Modelling, Identification and Control, 2010,11(1-2):5-14.
[13]CHEN Mou, GE Shu-zhi, How B V. Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearties [J]. IEEE Transactions on Neural Networks, 2010,21(5):796-812.
[14]TONG Shao-cheng, LI Chang-ying, LI Yong-ming. Fuzzy adaptive observer backstepping control for MIMO nonlinear systems [J]. Fuzzy Sets and Systems, 2009,160(19):2755-2775.
Adaptivefuzzyoutputfeedbackcontrolwithalmostdisturbancedecouplingfornonlinearsystems
LI Chang-ying*, WANG Wei
( School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China )
The problem of output feedback control with almost disturbance decoupling is investigated for a class of MIMO nonlinear uncertain systems, in which the states are unavailable for feedback. A structure, called nested lower triangular form, is introduced, which is much more general than strict feedback form. In the framework of combining fuzzy logic systems with the command filtered backstepping, fuzzy adaptive output feedback control design is proposed, and the command filters introduced can overcome the problem of explosion of complexity inherent in the traditional backstepping design methods. The proposed controller can not only achieve internal stability of the closed-loop system, but also diminish the effect of the disturbance on output in the sense ofL2gain. Subsequently, simulation results show the effectiveness of the proposed approach.
nonlinear systems; adaptive fuzzy control; command filters; almost disturbance decoupling; state observer
1000-8608(2014)01-0115-09
2013-04-21;
: 2013-11-05.
国家自然科学基金资助项目(61034003).
李长英*(1982-),女,博士,E-mail:xiaoya3691@163.com;王 伟(1955-),男,教授,博士生导师,E-mail:wangwei@dlut.edu.cn.
TP273
:A
10.7511/dllgxb201401018

