非理想界面功能梯度压电/压磁双材料中的SH界面波

赵 星, 刘响林, 刘 赛, 刘金喜

(1．石家庄铁道大学 工程力学系，石家庄 050043;2．石家庄铁道大学 数理系，石家庄 050043)

压电/压磁复合材料是由压电材料和压磁材料按照一定的方式复合而成的新型多功能材料，与传统的压电或压磁材料相比，它除了具有力-电和力-磁耦合效应，还具有一种新的乘积效应称为磁-电耦合效应，该效应来源于压电相和压磁相之间的相互作用，且比单相磁电材料高出几百倍[1]。利用该效应，压电/压磁复合材料可以用于制作磁电传感器、电场可调滤波器、延迟线、换能器等元器件，在信号处理、微波通信等领域显示出诱人的应用前景[2]。随着科技的发展及材料制备工艺的进步，人们将功能梯度材料的概念引入到压电/压磁复合材料中，发现利用材料的梯度变化不仅可以缓解应力集中，提高材料的断裂韧性[3]，还可以实现对材料磁电效应的调控和优化[4]。因此，近年来功能梯度压电/压磁复合材料的磁电性能及相关力学问题成为人们感兴趣的研究课题。

目前，已有文献对功能梯度梁、板、壳等基本结构的静态和动态变形[5-7]及弹性波在功能梯度磁电弹裂纹体或复合结构中的散射问题进行了详细的研究和报导[8-9]。弹性波在这种新材料中的传播特性对声表面波器件的设计及应用具有指导意义，因此近年来弹性波的传播特性也成为研究的热点。Yuan等[10]利用传递矩阵法分析了粘性流体覆盖时功能梯度压电/压磁复合结构中SH波的传播特性，讨论了材料梯度变化对SH波频散特性的影响。Cao等[11]对功能梯度压电/压磁复合板中的Lame波进行了研究。Tian等[12]假定材料沿厚度方向指数变化，分析了功能梯度压电/压磁层状半空间介质中SH波的传播特性。最近，Singh等[13]考虑材料参数沿平行于界面和垂直于界面两个方向变化，研究了压电/压磁双材料中SH界面波的频散特性。Li等[14]对功能梯度磁-电-弹半空间表面B-G波的传播特性进行了研究，发现材料的非均匀性会导致B-G波的频散，还可以改变B-G波的穿透深度。

以上所述文献中，均假定两种材料沿界面为理想连接，即力学、电学和磁学条件均连续。实际上，由于材料微观缺陷的存在、夹杂或加工、使用过程中的损坏等原因，界面处会变为非理想连接，这可能会对结构的力学性能产生不可忽视的影响。对于这类问题，Rokhlin等[15]提出的“弹簧”模型已被广泛用于表征界面的非理想程度。在弹簧模型中，界面处的应力定义为连续传递，而位移是间断的，且应力是位移间断值的线性函数。利用该模型，Huang等[16]讨论了非理想界面对磁电弹双材料中界面波传播特性的影响；Nie等[17]分析了非理想界面压电/压磁双层板中SH波的频散特性，Pang等[18]研究了压电/压磁复合结构中非理想界面处平面波的反射和折射。

本文利用“弹簧模型”，研究非理想界面无限大功能梯度压电/压磁双材料中SH界面波的传播特性，主要目的是揭示界面性能、界面电磁条件及材料梯度变化对界面波的影响。该问题的理论解对磁电弹复合材料在声波器件的设计和应用中具有参考价值。

1 问题的描述

由功能梯度压电(Functionally Graded Piezoelectric,FGPE)半空间和功能梯度压磁半空间(Functionally Graded Piezomagnetic,FGPM) 组成的双材料如图1所示，x1-x2平面是两种材料的各向同性面，x3轴垂直纸面向外，与材料极化方向一致。

图1 非理想界面功能梯度压电/压磁双材料

考虑沿x1方向传播的SH波，对于这种情况，只有面外的弹性场和面内的电磁场是耦合的，即为反平面磁电弹耦合问题。

(1)

(2)

在方程(1)和(2)中，σ和u分别为应力和位移；φ和D分别为电势和电位移；φ和B分别表示磁势和磁感应强度；G(x2)=c44(x2)、e(x2)=e15(x2)，h(x2)=h15(x2)分别表示弹性、压电和压磁常数；μ(x2)=μ11(x2)和κ(x2)=κ11(x2)分别为磁导率和介电常数；上标或下标“e”和“m”分别表示相应于压电材料和压磁材料的物理量。

在准静态电磁近似下，应力、电位移和磁感满足下面的平衡方程：

(3)

假定压电材料和压磁材料性能随x2轴成指数变化，即：

(4)

式中:βj表示材料j的梯度变化指数，G0、e0、h0、κ0、μ0、ρ0是材料在界面处的材料性能，上标或下标j表示相应于材料j的场量。

将式(1)、(2)和(4)代入式(3)，得到FGPE材料和FGPM材料的控制方程分别为：

(5)

(6)

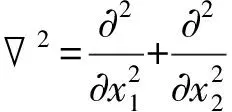
在界面x2=0处，假定两种材料之间的机械条件是非理想的，即应力连续而弹性位移不连续：

α[um(x1,0)-ue(x1,0)]

(7)

式中:α为表示界面粘结程度的常数。当α→∞时，表示两种材料沿界面是刚性连接的，相应的界面称为理想界面；当α=0时，表示两种材料沿界面是无机械约束的，相应的界面称为滑移界面。

对于沿界面的电磁学条件，考虑下面两种情况：

(1) 电位移、电势、磁感和磁势是连续的(简记为EMC)

(8)

(2) 电学短路和磁学开路(简记为SO)

(9)

另外，当x2→+∞时，应有(ue,φe,φe)→0，当x2→-∞时，有(ue,φe,φe)→0，所以βe<0，βm>0。

2 耦合波场的解和频散方程

对于沿x1方向传播的SH波，假定其一般解有如下形式：

(10)

式中:k为波数；c为波的传播速度，称为相速度；U、Ψ和Φ均为待定函数。

将式(10)分别代入到方程(5)和(6)，并考虑到无穷远条件，可得到

(11)

(12)

将式(11)和(12)分别代入方程(1)和(2)，可得到功能梯度压电和压磁半空间中的应力、电位移和磁感应强度为：

(13)

(14)

将上述解代入式(7)～(9)，可以得到两种界面条件条件下的频散方程：

EMC界面：

(15)

式中:

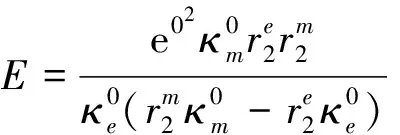
SO界面：

(16)

3 数值算例和讨论

利用上节推导的频散方程(15)和(16)，本节计算功能梯度压电/压磁双材料中界面波的传播性能。功能梯度压磁半空间为CoFe2O4材料，功能梯度压电半空间分别是PZT-4和BaTiO3材料。所选材料的性能在表1[19]中给出，表中的材料参数均表示材料在界面x2=0处的数值。

表1 材料常数

3.1 电位移、电势、磁感和磁势沿界面连续(EMC)情形

当α→∞时，EMC界面条件下频散方程(15)退化为理想界面时的频散方程:

(17)

这是文献[13]给出的结果。若令βe=0，βm=0，则方程(15)退化为非理想界面均匀双材料中界面波的频散方程:

(18)

式中:

当α=0时，界面为滑移界面，其频散方程为：

(19)

当波数k及梯度系数βe和βm确定时，方程(19)有两个确定解，分别为：

(20)

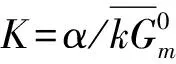
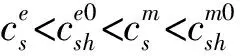
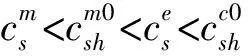
图2 PZT-4/CoFe2O4材料组合相速度c随参数的变化(EMC)

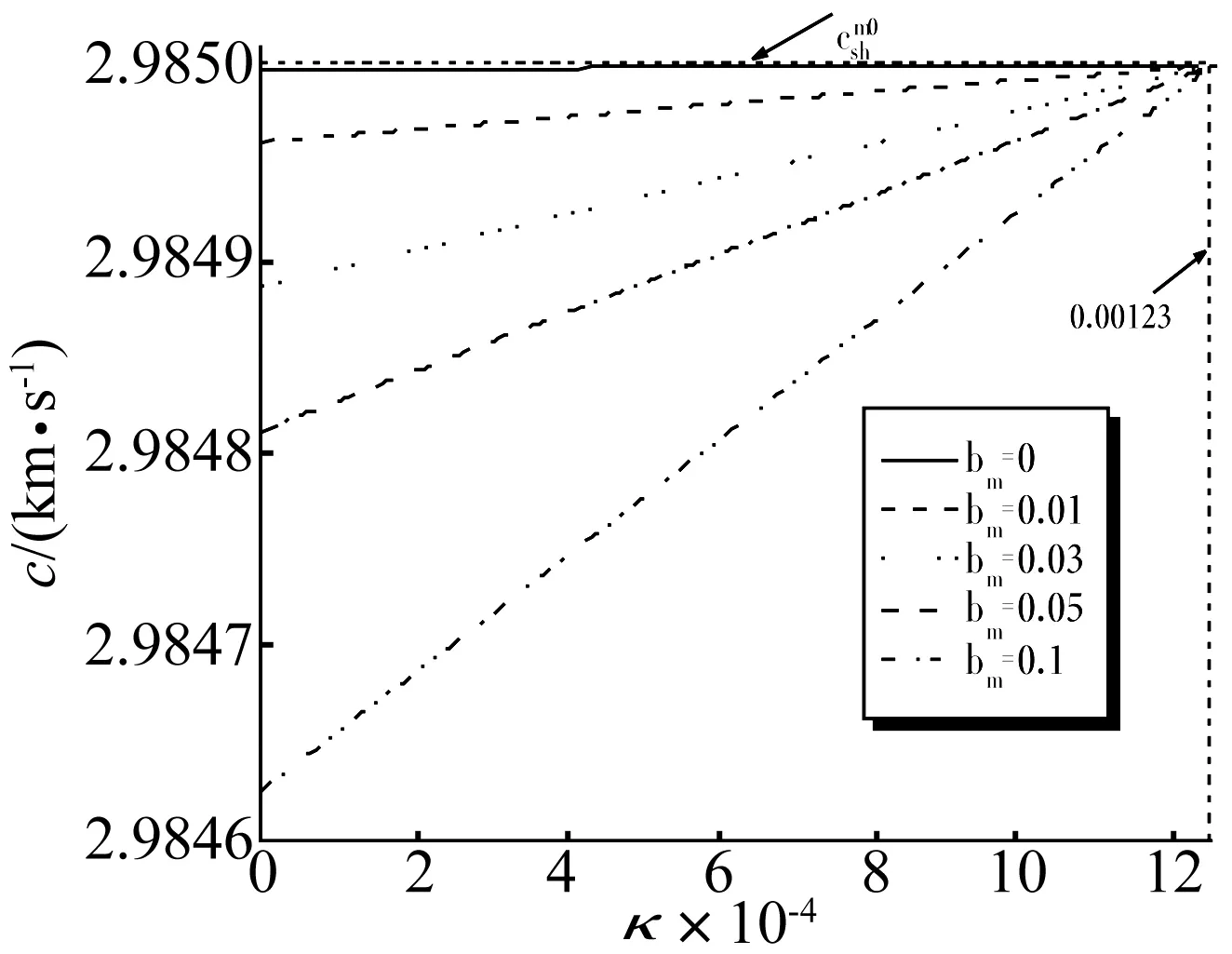
图3 BaTiO3/CoFe2O4材料组合相速度c随参数的变化规律(EMC)

3.2 电学短路和磁学开路界面(SO)情形

当α→∞时，SO界面条件下频散方程(16)退化为功能梯度材料理想界面时的频散方程:

(21)

若令βe=0，βm=0，则方程(16)退化了非理想界面均匀双材料中界面波的频散方程：

(22)

该方程已由Melkumyan等[19]给出，并说明界面处的非理想连接性能可以导致界面波的频散。

当α=0时，界面为滑移界面，其频散方程为：

(23)

当波数k及梯度系数βe和βm确定时，该方程有两个确定解，分别为：

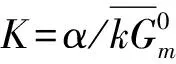
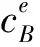
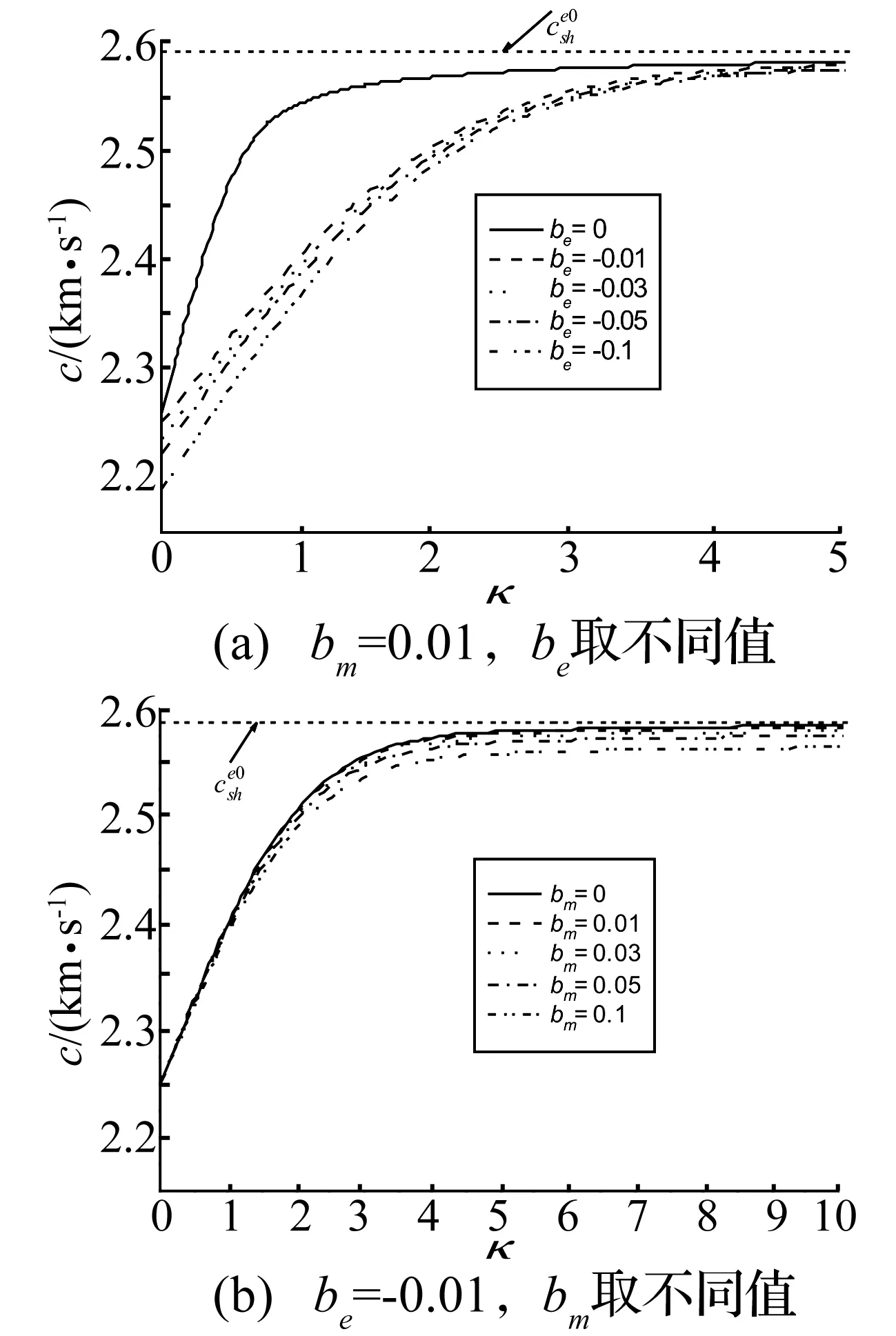
图4 PZT-4/CoFe2O4材料组合相速度c随参数的变化(SO)

图5 BaTiO3/CoFe2O4材料组合相速度c随参数的变化规律(SO)

4 结 论

研究了非理想界面功能梯度压电/压磁双材料中SH界面波的传播问题。考虑电位移、电势、磁感和磁势沿界面连续(EMC)和电学短路，磁学开路(SO)两种电磁界面条件，发现界面波是频散的，材料的非均匀性对界面波的相速度有重要影响，主要表现为:

(1) 界面波的相速度随界面约束强度的降低而减小，材料的非均匀性会降低界面波的相速度；

(2) 对于EMC界面情形，相速度主要受体波波速较小的材料性能的影响；

(3) 对于SO界面情形, 体波波速较小材料的梯度变化主要影响相速度的起始值，体波波速较大材料的梯度变化主要影响相速度的趋近值或相速度终止值所对应的K的临界值。

[1] Van S J. Product properties: a new application of composite materials[J]. Philips Research Reports, 1972, 27(5): 28-37.

[2] Nan C W, Bichurin M I, Dong S X, et al. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions[J]. Journal of Applied Physics, 2008, 103(3): 031101.

[3] 孙建亮,周振功,王彪.功能梯度压电压磁材料中的断裂问题分析[J].力学学报, 2005, 37(1): 9-14.

SUN Jian-liang, ZHOU Zhen-gong, WANG Biao. A permeable crack in functionally graded piezoelectric/piezomagnetic materials[J]. Acta Mechanica Sinica, 2005, 37(1): 9-14.

[4] Petrov V M, Srinivasan G. Enhancement of magnetoelectric coupling in functionally graded ferroelectric and ferromagnetic bilayers[J]. Physical Review B, 2008, 78(18): 184421.

[5] Bhangale, Rajesh K. Static analysis of simply supported functionally graded and layered magneto-electro-elastic plates[J]. International Journal of Solids and Structures, 2006, 43(10): 3230-3253.

[6] Yu T C, Nie G J, Zhong Z. Static and dynamic analyses of a functionally graded magnetoelectroelastic circular plate[C]. Symposium on Piezoelectricity Acoustic Waves and Device Applications. Nanjing, 2008:218-223.

[7] Mandal S K, Sreenivasulu G, Petrov V M, et al. Functionally graded piezomagnetic and piezoelectric bilayers for magnetic field sensors:Magnetoelectric interactions at low-frequencies and at bending modes[J]. Advances and Applications in Electroceramics, 2011, 226: 223-230.

[8] Liang J. Scattering of harmonic anti-plane shear stress waves by a crack in functionally graded piezoelectric/piezomagnetic materials[J]. Acta Mechanica Solida Sinica, 2007, 20(1): 75-86.

[9] Fang X Q, Liu J X, Wang D B, et al. Dynamic stress from a subsurface cavity in a semi-infinite functionally graded piezoelectric/piezomagnetic material[J]. Applied Mathematical Modelling, 2010, 34(10): 2789-2805.

[10] Yuan L L, Du J K, Yang L, et al. SH surface acoustic waves in layered functionally graded piezomagnetic/piezoelectric structures loaded with viscous liquid[C]. Proceedings of the 2011 Symposium on Piezoelectricity Acoustic Waves and Device Applications. Shenzhen, 2011:399-402.

[11] Cao X S, Shi J P, Jin F, Lamb wave propagation in the functionally graded piezoelectric-piezomagnetic material plate[J]. Acta Mechanica, 2012, 223(5): 1081-1091.

[12] Tian R M, Kong Y P, Liu J X. SH waves in functionally graded piezoelectric-piezomagneticmaterial structures[C]. The Symposium on Piezoelectricity, Acoustic Waves and Device Applications. Shanghai, 2012:1103-1110.

[13] Singh B M, Rokne J. Propagation of SH waves in layered functionally gradient piezoelectric piezomagnetic structures[J]. Philosophical Magazine, 2013, 93(14) : 1969-2013.

[14] Li P, Jin F, Qian Z H. Propagation of the Bleusteine Gulyaev waves in a functionally graded transversely isotropic electro-magneto-elastic half-space[J]. European Journal of Mechanics A/Solids, 2013, 37(27): 17:23.

[15] Rokhlin S I, Wang Y J. Analysis of boundary-conditions for elastic wave interaction with an interface between 2 solids[J]. Journal of the Acoustical Society of America, 1991, 89(5): 503-515.

[16] Huang Y, Li X F. Shear waves guided by the imperfect interface of two magnetoelectrmaterials[J]. Ultrasonics, 2010, 50(8): 750-757.

[17] Nie G Q, Liu J X, Fang X Q. Shear horizontal (SH) waves propagating in Piezoelectric/piezomagnetic bilayer system with an imperfect interface[J]. Acta Mechanica, 2012, 223(9): 1999-2009.

[18] Pang Y，Liu J X. Reflection and transmission of plane waves at an imperfectly bonded interface between piezoelectric and piezomagnetic media[J]. European Journal of Mechanics, 2011, 30(5): 731-740.

[19] Melkumyan A, Mai Y W. Influence of imperfect bonding on interface waves guided by piezoelectric/peizomagnetic composites[J]. Philosophical Magazine, 2008, 88(23): 2965-2977.