隔震斜交连续梁桥地震反应及环境温度影响研究

石 岩，王东升，孙治国，沈永林

(1.大连海事大学 道路与桥梁工程研究所，辽宁 大连 116026；2.辽宁省公路工程重点实验室，辽宁 大连 116026；3.云南省交通规划设计研究院,昆明 650011)

为满足地形、线路需要，斜交桥成为高速公路、城市高架桥中较常见桥型。历次破坏性地震中，斜交桥震害均较突出：如Foothill Boulevard立交桥排架墩严重破坏[1]；Gavin峡谷立交桥发生落梁[2]；南坝大桥、映秀岷江大桥、兴文坪大桥、渔子溪1号桥等斜交桥均遭受不同程度破坏[3]；智利地震中斜交桥破坏非常严重[4]。纵观斜交桥震害主要表现为落梁、梁体平面内旋转并与桥台、挡块碰撞破坏等。对震害问题已有相关研究：Maragakis等[1]认为斜交角、梁体与桥台碰撞主导斜交桥反应；Saadeghvaziri等[5]通过对多跨简支梁桥进行地震易损性评估发现梁体与桥台间碰撞增大多跨简支斜梁桥支座剪力需求，会致支座发生剪切破坏；Ghobarah等[6]认为斜交桥倒塌原因为主梁弯扭耦合或桥墩压坏所致；Tirasit等[7]研究表明梁体与桥台间碰撞引起梁体面内转动增大桥墩扭矩；Dimitrakopoulos[8]提出考虑斜摩擦、多接触的非光滑刚体模型分析斜桥碰撞反应；Kaviani等[9]发现斜交角越大越易引起旋转落梁，但桥台挡块对防止落梁起关键作用；何健等[10-11]分析连续斜交梁桥碰撞效应及梁体旋转效应。

隔震技术已成为有效抗震减灾措施，在桥梁工程中得以广泛应用，其有效性[12-13]亦在若干次实际地震中得以证明。如Sierra Point立交桥采用隔震技术在Loma Prieta地震中表现良好[14]。目前橡胶类隔震支座应用较多，据生产商提供的支座力学特性值进行隔震设计并预测其地震反应；但桥梁支座一般置于上、下部结构之间，即直接裸露在所处环境，环境温度发生变化时，其力学特性与设计值(常温下)可能存在较大差异。若设计中不考虑温度对隔震支座力学特性影响，则会有一定安全隐患[13]。如日本东北部的On-netoh新桥引桥，3个中墩用铅芯橡胶支座，在Kushiro-oki地震中虽未发生严重破坏，但通过对距新桥不足200 m旧桥处采集的强震记录对新桥计算分析发现，-20℃时墩底峰值弯矩较设计值(20℃)几乎大1倍[15]。

我国气候温差较大，北部、西部地区冬季气温较低，东北及西北大部分地区冬季温度在-10℃以下，故隔震桥梁设计考虑温度(低温)影响至关重要。对隔震桥梁研究多针对正交桥，对隔震斜交桥并考虑温度影响研究尚少见。为此本文以一座用铅芯橡胶支座的四跨连续斜交梁桥为工程背景，基于OpenSees地震分析平台建立考虑梁体与桥台碰撞作用的动力分析模型，探讨桥墩位移、墩底反力、碰撞力及梁体旋转度与斜度关系以及梁端碰撞力分布规律，对比采用两种修正方法[13,20]差异，讨论隔震桥梁地震反应与环境温度、斜度关系。

1 温度对铅芯橡胶支座力学特性影响

低温会使橡胶变硬。一般认为橡胶的低温效应包括达到热平衡过程中形成的瞬时热硬化效应与时间相关的结晶硬化效应。Roeder等[16]给出与冷却时间相关的橡胶支座低温性能变化曲线。Yakut等[17]研究小型氯丁橡胶及天然橡胶支座低温下剪切模量与室温下剪切模量变化规律。李慧等[18-19]研究低温环境下叠层橡胶支座特性变化及对建筑结构地震反应影响。胡紫东等[20]通过铅芯橡胶隔震支座温度相关性试验回归获得支座初始刚度、屈服后刚度及屈服强度的温度公式：

(1)

(2)

(3)

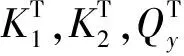
Constantinou等[13]通过理论分析与试验研究，总结考虑老化、扰动及温度影响的隔震橡胶支座力学特性修正系数，且被AASHTO隔震设计指南[21]采纳。铅芯橡胶支座所用橡胶阻尼较低，支座内部铅芯主要贡献滞回耗能，橡胶老化及扰动对支座力学特性影响较小。铅芯橡胶支座温度修正系数[13]见表1。

表1 温度特性修正系数

2 隔震桥梁模型及参数

2.1 工程背景

本文以一座4×25 m连续斜交桥为工程背景进行研究。该桥上部结构为4片连续小箱梁，桥墩为双柱式规则排架墩，截面为圆形直径1.5 m，桥墩高度分别为8 m，12 m，8 m。全桥采用双向隔震，每个桥墩(台)设4个铅芯橡胶支座隔震，常温力学参数见表2。为充分发挥隔震支座隔震、耗能特性，隔震桥梁上部结构需较大运动空间，当梁体运动受横向限位装置(如挡块等)约束时会难以发挥隔震效果甚至起相反作用，如日本Yama-age桥、美国Sierra Point立交桥、台湾Bai-Ho桥即因此原因在地震中反应放大[12]。为此，本文设梁体沿横桥向有足够运动间隙，桥台处纵向设伸缩缝且考虑梁体与桥台背墙的相互作用。

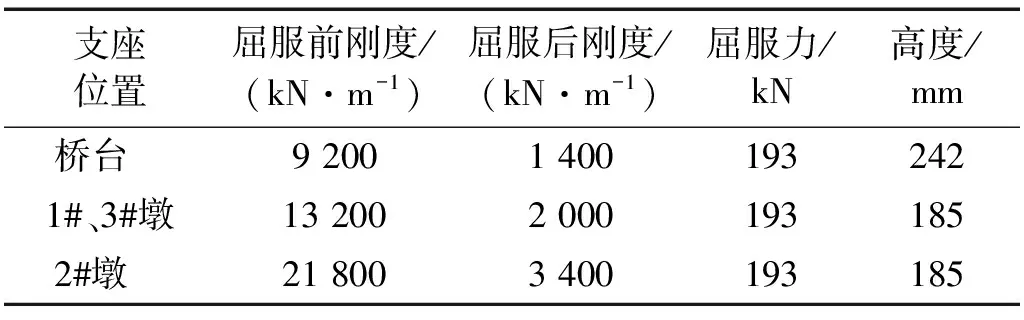
表2 铅芯橡胶支座参数

2.2 动力分析模型

本文基于OpenSees地震分析计算平台，建立三维动力分析模型见图1。混凝土结构阻尼比取5%，并采用Rayleigh阻尼。不考虑桥梁结构-桩-土作用及桥台-填土间相互作用影响，铅芯橡胶支座采用双线性橡胶支座单元。上部结构离散为4梁式模型，梁与梁之间用间隔5 m的刚性横梁连成整体，主梁用三维弹性梁单元模拟。桥墩用纤维模型单元，保护层混凝土及核心区混凝土用Concrete04模拟，卸载、重加载规则按Filippou修正后Karsan-Jirsa模式确定；钢筋用Steel02模拟，应力-应变关系基于Giuffre-Menegotto-Pinto模型，并考虑钢筋加载卸载循环过程中包兴格效应影响。

结构(或构件)间碰撞问题备受关注[22]。地震碰撞模拟中，接触单元法力学概念清晰、易与软件结合，应用较广[23]。为考虑梁体与桥台背墙间碰撞作用，在每片箱梁与桥台间设置接触单元，两侧共设8个碰撞单元，0#桥台处碰撞单元编号由锐角到钝角依次为P1、P2、P3、P4，4#桥台处编号由锐角到钝角依次为P5、P6、P7、P8。相对位移超过初始间隙(0.05 m)时，梁体与桥台发生碰撞。

图1 隔震斜交桥模型示意图

常用接触单元法力学模型有线性模型、Kelvin模型、Hertz模型、Hertz-damp模型等。其中 Hertz-damp模型[24]能较好模拟碰撞时的能量耗散应用较广[23]。该模型恢复力力学特性见图2。碰撞中能量损失为

(4)

式中：kh为碰撞刚度，按单片箱梁轴向刚度计算，取2.0×105kN/m；n为Hertz刚度系数，取3/2；e为恢复系数，混凝土材料取0.65；δm为碰撞过程中最大侵入深度，取0.01 m[24]。有效刚度与碰撞刚度关系为

(5)

屈服位移与最大侵入深度关系为

δy=aδm

(6)

式中：a为屈服系数，取0.1。

由碰撞过程能量守恒可得初始刚度K1及屈服后刚度K2为

(7)

(8)

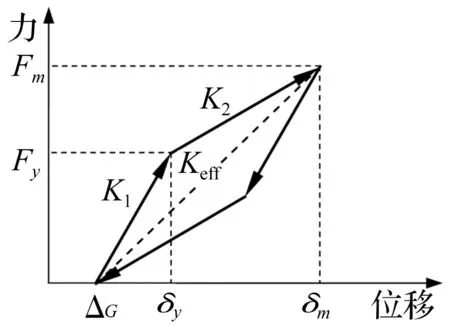
图2 Hertz-Damp碰撞模型

2.3 地震动输入

本文由小型工程用强震记录数据库[25]中选硬土场地10组地震动记录，每组记录含两方向水平分量。时程分析选较大加速度分量并将加速度峰值(PGA)调整为0.4 g后沿纵桥向(图1、图3轴x方向)输入；较小加速度分量沿横桥向(轴y方向)输入，并按纵向调幅比例调整PGA。纵桥向、横桥向地震反应指x，y方向地震反应，分析时皆以10组地震动记录的反应峰值平均值为讨论指标，见表3。

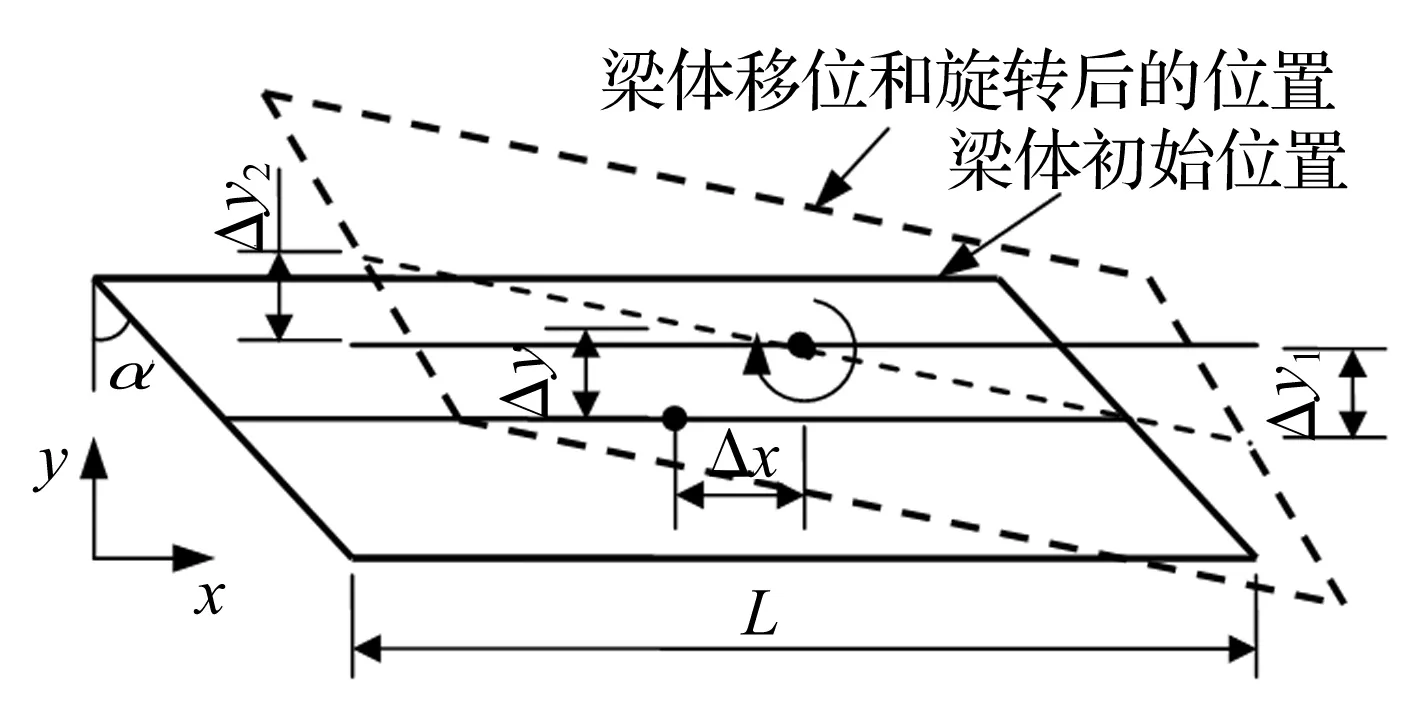
图3 梁体运动示意图

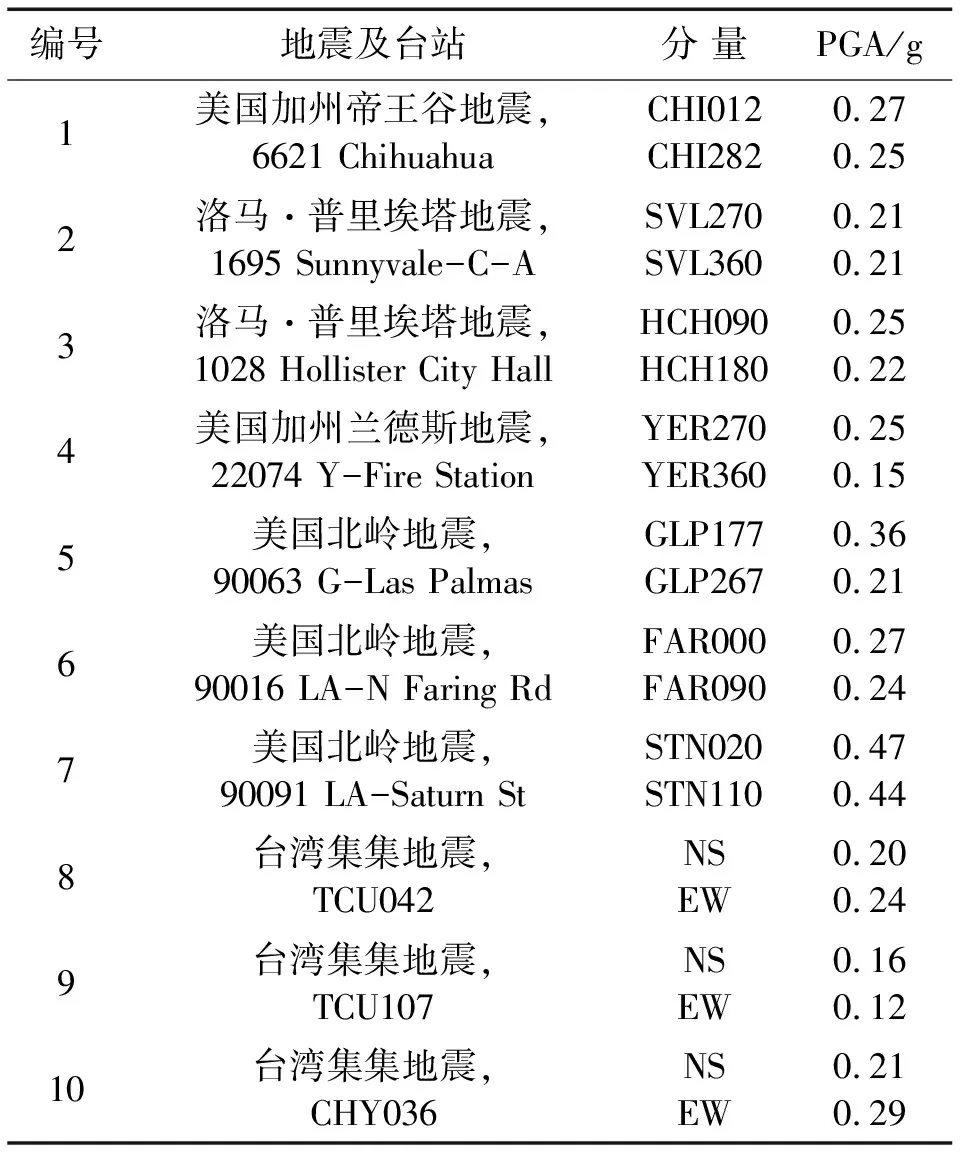
表3 中硬(软)土场地地震记录

3 斜交隔震桥梁地震反应

斜交桥梁体(纵向)中心线垂线与支座横向中心线夹角称斜度α。为更广泛考察斜交隔震桥梁地震反应，通过改变算例桥梁的斜度(α=0°～60°)，探讨桥墩位移、墩底反力、碰撞力及梁体旋转度随其变化情况，在此基础上改变环境温度，讨论隔震斜交桥在环境温度影响下地震反应特性。

3.1 梁体-桥台碰撞作用影响

分别考虑与不考虑梁体与桥台碰撞作用时，分析获得隔震桥梁地震反应，8个碰撞单元碰撞力峰值与斜度关系见图4。由图4看出，① 斜度为0°(即正交桥) 时，各碰撞单元碰撞力基本一致；② 随斜度的增大，碰撞力有先增后降趋势，锐角处α=10°时最大、钝角处α=20°时最大；③ 斜度大于零时，从梁体锐角边向钝角边碰撞力依次增大，即钝角处碰撞力最大、锐角处最小；④ 除斜度α=60°时，两桥台关于梁体平面中心点(梁体平面对角线交点)对称的碰撞单元碰撞力不相等。

图4 碰撞力与斜度关系

为考察梁体与桥台碰撞作用对桥墩及主梁地震反应影响，分别考虑纵桥向碰撞与否的桥墩顶部位移及梁体中部位移(2#墩顶处)与斜度变化趋势见图5、图6。由两图看出，① 无论考虑碰撞与否，纵桥向墩顶位移随斜度增大有先增后减趋势，即斜度在20°以内时墩顶位移略有增大；但大于20°时，则有明显下降趋势；以2#墩不考虑碰撞为例，α=60°斜交桥墩顶位移较正交时减小30%；② 无论考虑碰撞与否，桥墩顶部横向位移随斜度增大明显增大，α=60°斜交桥边墩、中墩顶部位移较正交时分别增大5.5倍及2.5倍；③ 考虑梁体与桥台背墙碰撞作用等于限制上部结构位移，桥墩纵向位移明显减小，减小幅度受斜度影响不大；碰撞作用会适当减小墩顶横桥向位移，且随斜度的增大减小幅度略有增加；④ 无论考虑碰撞与否，随斜度的增大(α>20°)梁体中部纵向位移略减小，而横向位移则增大。同样考虑碰撞后两水平方向位移均会减小。

为表征强震下斜交桥梁体在平面内的旋转程度，本文将图3中梁体两端横向相对位移之和(Δy1+Δy2)与梁长(L)比值定义为梁体旋转度(r)，即r=(Δy1+Δy2)/L；r越大，表明梁体在平面内的旋转位移越大[11]，在一定程度上反映出梁体两侧端部横向位移差异。旋转度r与斜度的关系见图7。由图7看出，不考虑梁体与桥台背墙的碰撞作用时，梁体旋转度基本不受斜度影响；考虑碰撞作用后梁体旋转度随斜度的增大明显增大，即梁体两端横向位移差异显著增大。因此，在双向水平地震作用下，梁体纵、横向反应及平面内扭转反应的耦合作用导致梁体发生纵、横向移动及平面内旋转；当梁体与桥台背墙(纵向)相对位移超过初始间隙时便发生碰撞，但由于梁体旋转使钝角处(P4，P8)先发生碰撞(碰撞力时程曲线)，从而进一步加剧梁体旋转，使钝角处碰撞力更强烈，过大的梁体横向运动、旋转可能致锐角处先失去支承，进而导致落梁。梁体旋转使桥墩扭矩显著增大，斜度越大(α>15°)越明显，见图8。

3.2 环境温度影响

3.2.1 两种温度修正方法比较

为考察环境温度(低温)对铅芯橡胶支座力学特性影响，本文采用两种修正方法[13,20]，以斜度30°及考虑碰撞作用的斜交隔震梁桥为例，分析环境温度对隔震斜交桥地震反应影响及差别。分析地震反应量包括墩底弯矩、桥墩位移，见图9、图10。两图中反应比表示(同一斜度斜交桥)考虑环境温度影响时地震反应量与常温下地震反应量之比。其大于1时，表面环境温度放大地震反应；反之则减小地震反应。在第1组地震动作用下两种修正方法对应的桥台处支座滞回曲线见图11。由图9～图11看出，低温环境下隔震桥梁地震反应明显被放大，且温度越低放大程度越明显。由保护桥墩角度，前种修正方法较后者保守。

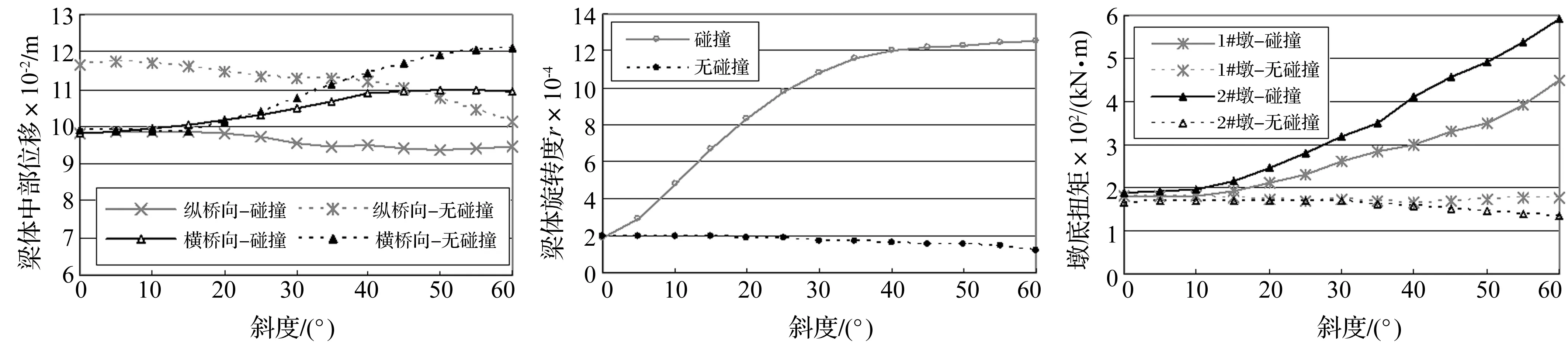
图6 梁体中部位移与斜度关系

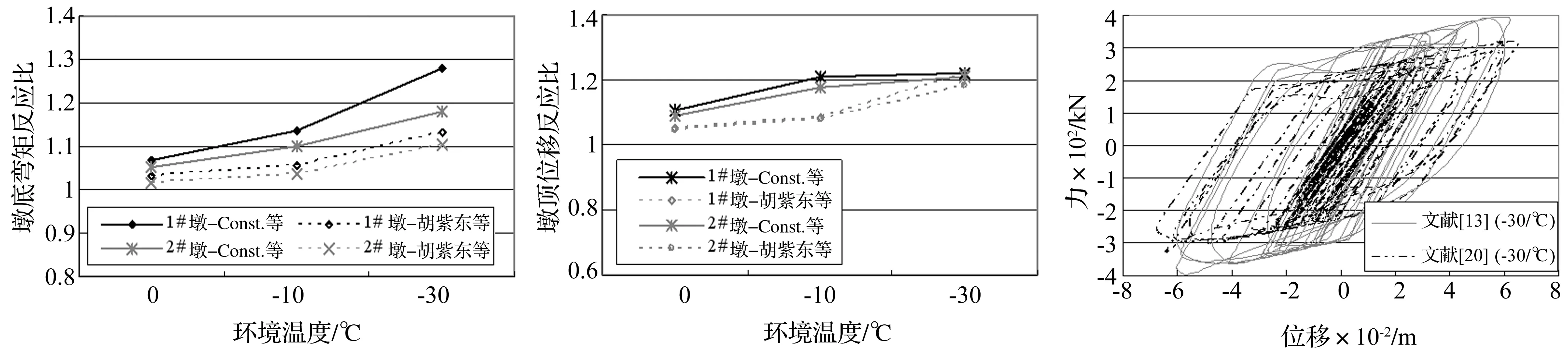
图9 墩底弯矩与环境温度关系

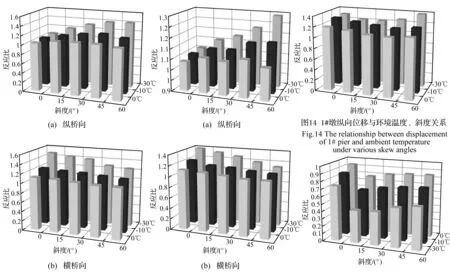
图12 1#墩墩底剪力与环境温度、斜度关系

3.2.2 地震反应比与环境温度、斜度关系

为考察环境温度(低温)对不同斜度斜交桥隔震反应影响，采用文献[13]修正方法对隔震支座力学特性进行修正，并考虑梁体-桥台碰撞作用，分析获得不同地震反应比与环境温度、斜度关系。桥墩(1#墩)墩底剪力及弯矩变化见图12、图13。由两图看出，①环境温度越低，墩底反力放大程度越明显；综合纵桥向、横桥向墩底反力反应比知，若不考虑环境温度影响，在0℃、-10℃、-30℃低温下会分别低估10%、20%、40%的墩底剪力及弯矩；②同一环境温度下纵桥向墩底反力(剪力、弯矩)放大程度随斜度的增加而增加，横桥向则相反，且斜度对纵桥向影响大于横桥向。桥墩(1#墩)墩顶纵向位移反应比随环境温度、斜度变化见图14。由图14看出，因环境温度对纵桥向、横桥向墩顶位移影响趋势相同，此处仅给出纵桥向结果。一般正交桥(α=0°)墩顶位移反应比最大，如在-30℃低温下1#墩顶纵向位移被放大30%；斜度大于零时，随斜度的增加其放大程度略有增大或接近，如在-30℃低温下斜度为60°的隔震桥墩顶纵向位移放大40%。梁体旋转度变化见图15。由图15看出，环境温度使梁体旋转度减小，且温度越低减小程度越大，主要因隔震桥梁变形主要集中于隔震支座，而低温使隔震支座刚度增大、变形减小；斜度α=15°时旋转度反应比最小，表明此时环境温度对其影响最显著。

考察桥墩承受扭矩情况，虽不同工况下中墩(2#)扭矩大于边墩(1#和3#)，但环境温度对边墩扭矩影响大于中墩，如1#墩在-30℃低温下斜度α=15°，其扭矩最大被放大50%，见图16。隔震桥梁在地震中变形主要集中在隔震支座，故隔震支座在地震中工作状况决定整个结构的抗震性能。本桥系全桥双向隔震，桥台处支座在地震中变形最大，桥台处支座在不同环境温度、斜度下变形见图17。由图17看出，环境温度越低支座,变形越小，随斜度的增加支座纵向位移略有减小、横向位移明显增大；支座最大变形为0.13 m(剪应变为0.56)，支座处于安全状态。

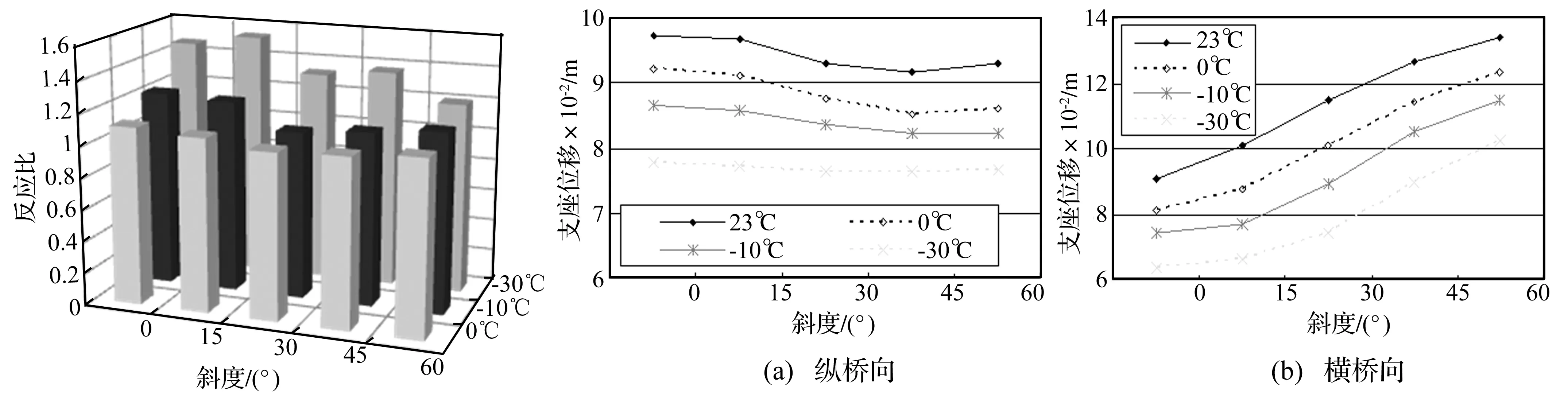
图16 1#墩扭矩与环境温度、斜度关系

4 结 论

本文通过对四跨LRB隔震斜交连续梁桥研究，利用非线性时程分析方法探讨斜度、环境温度对地震反应影响，结论如下：

(1) 梁体双向水平与平面内旋转运动耦合使梁体与桥台在其钝角处先发生碰撞，而碰撞作用能加剧梁体旋转；斜度越大梁体越易发生旋转。

(2) 梁体与桥台碰撞力由梁体锐角边向钝角边依次增大，钝角处碰撞力最大；随斜度的增大各接触点碰撞力先增后减。

(3) 随斜度的增大横桥向桥墩位移增大，而纵桥向桥墩位移则先增后减，碰撞作用能适当约束桥墩位移反应。

(4) 低温环境会引起支座特性改变，放大桥墩的地震反应，温度越低放大程度越明显；不考其影响时，在0℃、-10℃、-30℃条件下较常温(23℃)分别低估10%、20%、40%的墩底剪力及弯矩。低温环境会较大增加桥墩扭矩。

(5) 低温环境将减少斜交桥梁体平面内旋转，温度越低减小程度越大。斜度α=15°时环境温度影响最显著。

[1] Margakis E A, Jennings P C.Analytical models for the rigid body motions of skew bridges[J].Earthquake Engineering Structure Dynamics,1987, 15(8):923-944.

[2] Mitchell D, Bruneau M, Saatcioglu M, et al.Performance of bridges in the 1994 Northridge earthquake[J].Canadian Journal of Civil Engineering, 1995, 22(2): 415-427.

[3] 李乔,赵世春.汶川大地震工程震害分析[M].成都:西南交通大学出版社,2009.

[4] Kawashima K, Unjoh S, Hoshikuma J, et al.Damage of bridges due to the 2010 Maule, Chile, Earthquake[J].Journal of Earthquake Engineering,2011,15(7):1036-1068.

[5] Saadeghvaziri M A, Yazdani-Motlagh A R.Seismic behavior and capacity/demand analyses of three multi-span simply supported bridges[J].Journal of Structural Engineering, 2008,30(1):54-66.

[6] Ghobarah A A, Tso W K.Seismic analysis of skewed highway bridges with intermediate supports[J].Earthquake Engineering Structure Dynamics,1974,2(3): 235-248.

[7] Tirasit P, Kawashima K.Seismic torsion response of skewed bridge piers[J].Journal of Earthquake Engineering, 2006(28):1-8.

[8] Dimitrakopoulos E G.Seismic response analysis of skew bridges with pounding deck-abutment joints[J].Journal of Structural Engineering, 2011,33(3):813-826.

[9] Kaviani P, Zareian F, Taciroglu E.Seismic behavior of reinforced concrete bridges with skew-angled seat-type abutments[J].Engineering Structures, 2012,45:137-150.

[10] 何健,叶爱君.连续斜交梁桥地震下碰撞效应分析[J].中南大学学报(自然科学版),2012,43(4):1475-1481.

HE Jian, YE Ai-jun.Seismic response of continuous skew bridges with pounding effect[J].Journal of Central South University (Science and Technology), 2012,43(4):1475-1481.

[11] 卢明奇，杨庆山，李英勇.地震作用下斜交连续梁桥碰撞效应分析[J].中国矿业大学学报,2012,41(2): 289-292.

LU Ming-qi, YANG Qing-shan, LI Ying-yong.Collision effect analysis of skew continuous bridge under seismic response[J].Journal of China University of Mining & Technology, 2012,41(2): 289-292.

[12] Lee G C, Kitane Y, Buckle I G.Literature review of the observed performance of seismically isolated bridges[R].New York: Multidisciplinary Center for Earthquake Engineering Research,Research Progress and Accomplishments, 2001: 51-62.

[13] Constantinou M C, Whittaker A S, Kalpakidis Y, et al.Performance of seismic isolation hardware under service and seismic loading (MCEER 07-0012)[R].New York: Buffalo, 2007.

[14] National research council.Practical lessons from the loma prieta earthquake[M].Washington D.C.: National Academy Press, 1994.

[15] Sato M, Nishi H, Kawashima K, et al.Response of on-netoh bridge during kushiro-oki earthquake of january 1993, nceer-94-0009[R].New York: National Center for Earthquake Engineering Research, 1994.

[16] Roeder, C W, Stanton, J F, Taylor A W.Performance of elastomeric bearings, No.298[R].Washington D.C.: Transportation Research Board, 1987.

[17] Yakut A, Yura J A.Parameters influencing performance of elastomeric bearings at low temperatures[J].Journal of Structural Engineering, 2002,128(8):986-994.

[18] 李慧,邓学晶,杜永峰,等.寒区叠层橡胶隔震支座拟静力试验研究[J].低温建筑技术, 2003(4): 33-35.

LI Hui, DENG Xue-jing, DU Yong-feng, et al.Pseudo- static experimental study of rubber isolator under low temperature[J].Low Temperature Architecture Technology, 2003(4): 33-35.

[19] 由世岐,刘斌,楼永林.低温环境对叠层橡胶支座变形特性影响的试验研究[J].东北大学学报,2005(3): 297-299.

YOU Shi-qi, LIU Bin, LOU Yong-lin.Low-temperate effect on deformation behavior of laminated rubber isolators[J].Journal of Northeastern University,2005(3): 297-299.

[20] 胡紫东,李黎,聂肃非.考虑温度相关性的LRB隔震桥梁地震响应分析[J].振动与冲击,2011,30(9): 40-45.

HU Zi-dong, LI Li, NIE Su-fei.Seismic response of isolated bridges considering temperature effect[J].Journal of Vibration and Shock,2011,30(9): 40-45.

[21] American association of state highway and transportation officials.guide specifications for seismic isolation design (3rd edition)[S].Washington, D.C.: AASHTO, 2010.

[22] 张文学,吴海军,陈士通.橡胶缓冲装置对斜拉桥与引桥碰撞影响研究[J].振动与冲击,2013,32(7):151-154.

ZHANG Wen-xue, WU Hai-jun, CHEN Shi-tong.Influence of rubber buffer devices on collision between a cable-stayed bridge and its approach span[J].Journal of Vibration and Shock,2013,32(7):151-154.

[23] 许祥,鞠三,刘伟庆,等.桥梁结构地震碰撞分析模型的碰撞刚度计算方法研究[J].振动与冲击,2013,32(12): 31-39.

XU Xiang, JU San, LIU Wei-qing.Computation methods for impact stiffness of earthquake-induced bridge pounding models[J].Journal of Vibration and Shock, 2013,32(12):31-39.

[24] Muthukumar S, Desroches R.A Hertz contact model with non-linear damping for pounding simulation[J].Earthquake Engineering & Structural Dynamics, 2006,35(7):811-828.

[25] 王东升,李宏男,王国新,等.弹塑性地震反应谱的长周期特性研究[J].地震工程与工程振动,2006,26(2):49-55.

WANG Dong-sheng, LI Hong-nan, WANG Guo-xin, et al.Study on characters of long period portion of inelastic spectra[J].Earthquake Engineering and Engineering Vibration, 2006,26(2):49-55.