基于Kriging模型的钢管混凝土连续梁拱桥有限元模型修正

胡俊亮，颜全胜，郑恒斌，崔楠楠，余晓琳

(华南理工大学 土木与交通学院,广州 510640)

由于桥梁结构发展的复杂化，导致较难直观判断构件受力状况。有限元分析方法虽能满足大型复杂结构分析需要，但亦较难直接建立与试验结果匹配的有限元模型。Mottershead等[1]认为有限元模型不精确、与试验结果不相匹配原因为：① 常出现于结构有强烈非线性行为时的模型结构误差；② 不合适的边界条件及在简化模型时不精确假设等的模型参数误差；③ 发生于对复杂结构离散化处理时，有限元模型所得阶数不能完全反映结构真实状况，仅为实际结构阶数一部分的模型阶次误差。因此，注意力转移至基于试验结果的有限元模型修正研究。通常由现场试验与有限元模型分析获得结构固有特性。虽现场试验因环境噪声干扰，测量仪器误差及试验误操作等会致结果存在一定误差，但仍可认为现场试验所得结构特性能在一定程度上反映结构的真实状况。因此，现场测试结果与有限元模型分析结果不匹配时，需对有限元模型进行修正以期能反映结构的真实状况。

1 有限元模型修正方法

有限元模型修正方法可分为两类，即矩阵型模型修正方与参数型模型修正法。整体结构矩阵型修正方法[2]以有限元模型质量矩阵M及刚度矩阵K加权范数最小化为目标函数，以振型正交性、M、K对称性为约束条件，采用有约束的最小化求解方法进行模型修正。该修正方法采用由振动试验所得结构特征向量与振型矩阵(扩阶后振型矩阵)。因此，模型修正精度直接与扩阶后振型精度相关。通过整体结构矩阵修正所得结构矩阵会将原有带状、稀疏特性改变成满秩矩阵，甚至有些元素变负值，导致所得结构矩阵物理意义不明显，甚至产生虚假模态。因此，诸多研究据存在问题提出解决方法。Kabe[3]引入元素相关性概念，提出保持原模型带状、稀疏特性方法；向锦伍等[4]提出通过求解结构矩阵的误差矩阵，定位误差较大单元进行特定修改，保持原结构矩阵特性；但此方法缺点为经修正的结构矩阵无法反馈到现有通用有限元计算软件中，适用性受到一定限制。参数型有限元模型修正方法选特定参数进行模型修正，使修正后有限元分析与试验结果误差最小，物理意义明确。因此，参数型模型修正方法获得广泛发展。所选修正参数为弹性模量、材料密度、截面面积等。

参数型修正方法包括频响函数法[5-8]、模拟退火算法[9-11]、神经网络法[12-14]、遗传算法[15-17]、基于商业软件Ansys二次开发技术的优化理论方法[18-20]及统计方法[21-27]等。频响函数法无需模态分析，可避免将模态参数识别误差带入模型修正；而其缺点在于需结构完整频响函数值，因此又引入模型扩展者缩聚所致误差。模拟退火算法计算过程简单、鲁棒性强，能以较大概率求得全局最优解。但其收敛速度缓慢，算法性能与初始值密切相关。神经网络方法以其强大的非线性映射能力、容错能力及鲁棒性在有限元模型修正领域广泛应用；但其要求训练样本足够多，网络类型选取及隐含层数、节点数量、初始值确定无理论依据等缺陷其应用亦受到限制。遗传算法为高效并行的全局寻优算法，但同模拟退火算法亦存在收敛速度缓慢的缺点。基于商业软件二次开发技术的优化理论方法能解决其它模型修正方法难以考虑的结构非线性影响及预应力效应问题，但亦存在计算效率较低、不能保证收敛到全局最优解的缺陷。统计方法考虑统计量的不确定性与统计分布特征，利用谱密度估计统计特性，获得用多变量高斯分布精确近似模态参数概率密度函数，计算高斯分布均值与方差可获得模态参数的最优估计及与之联系的不确定度，将不确定度用于有限元模型修正。文献[26]用两实际结构模型修正过程说明基于贝叶斯证据统计方法的有效性，认为影响模型修正参数选择的两重要因素为有限元模型逼近测量数据方法及每个模型对测试数据信息量提取的多寡，对模型修正精度有直接影响。

Kriging法为数学、地质学广泛使用、基于随机过程的统计预测法，其据区域内若干信息样品的某种特征数据对该区域同类特征未知数作线性无偏、最小方差估计，具有平滑效应及估计方差最小的统计特征[28]。Kriging法由南非地质学者Krige于1951年提出，用于确定矿产储量分布。Sacks等[29]第一次将Kriging方法应用于结构设计。Romero等[30-31]将其应用于结构可靠度问题。鉴于Kriging模型优越的模拟性能，本文将其用于有限元模型修正，并与遗传算法、神经网络方法对比，由实例验证该方法精度与高效性。

2 Kriging模型

Kriging作为线性回归分析的改进技术，包含线性回归与非参数部分，其中非参数部分为高斯平稳随机过程，因而 Kriging模型一般由两部分组成，即多项式与随机分布，即

(1)

fT(x)β=β1f1(x)+β2f2(x)+…βmfm(x)=

[f1(x)…fm(x)]β

(2)

式中：β为回归系数；f(x)为变量x多项式函数；m为fi(x)数目。

在设计空间中f(x)提供模拟的全局近似，而Z(x)提供模拟的局部近似。Z(x)为均值为零协方差非零的高斯平稳随机过程，服从正态分布N(0,σ2)，Z(x)协方差矩阵为

(3)

式中：R(θ,xi,xj)为样本点中任意两样本点xi，xj空间相关函数，对模拟精度起决定性作用；θ为相关函数参数；n为试验点数。

Y={y1(x),y2(x),…,yn(x)}

(4)

据输出函数，未知参数β，σ2可估计为

(5)

(6)

式中：F为含每个试验点f(x)估值向量；R为每个试验点相关函数矩阵:

(7)

(8)

本文用遗传算法求解最优θ。获得θ后，响应最佳线性无偏预测可写为

(9)

(10)

式中：rT(x)为每个试验点与待测点间相关函数向量，表示为

rT(x)={R(x,x1),…,R(x,xn)}

(11)

(12)

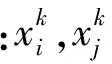
相关函数模型核函数选择取决于使用者，本文亦采用计算效果较好的高斯函数作为相关模型核函数

(13)

3 算例

3.1 算例1

用Kriging模型方法对文献[17]中平面桁架进行有限元模型修正工作。结构形式见图1，各杆件均为内径5.4 cm、外径8.5 cm圆钢管。设初始弹性模量E= 2.1E11 Pa，初始密度ρ=7 800 kg/m3，泊松比0.3。

图1 桁架平面图(单位cm)

桁架模型优化结果[17]与本文Kriging模型方法模型优化结果见表1。以材料弹性模量与密度为设计参数。设结构设计参数为X～N(μ,σ)的正态分布，μ为各设计参数初值，σ=μα为变量标准差，α为设计参数变异系数，本例两设计参数变异系数均取5%。将100组设计变量代入Ansys有限元模型，获得100组有限元分析结果。用前2阶频率为训练样本，训练样本数为100。获得模型优化结果(表1)及优化后设计参数为弹性模量E=1.92E 11 Pa，密度ρ=8 024.1 kg/m3。由表1看出，Kriging模型对前3阶频率优化结果优于遗传算法[17]，且前6阶优化结果误差均在2%以内。Kriging模型优化方法计算精度较高。

表1 桁架模型优化结果对比 (单位:Hz)

3.2 算例2

本文对一座大跨度钢管混凝土连续梁拱组合体系桥-杜坑特大桥进行有限元模型修正。该桥跨径58.4 m+ 128 m+58.4 m，桥型见图2。主梁为预应力混凝土结构。拱肋为钢管砼结构，采用等高度哑铃形截面，截面高度2.8 m，拱肋弦杆及缀板内填充微膨胀混凝土。拱肋计算跨径l=128.0 m，设计矢高f=25.6 m。全桥共14对吊杆，每根吊杆为双吊索形式，吊杆统一直径为Φ=85 mm。

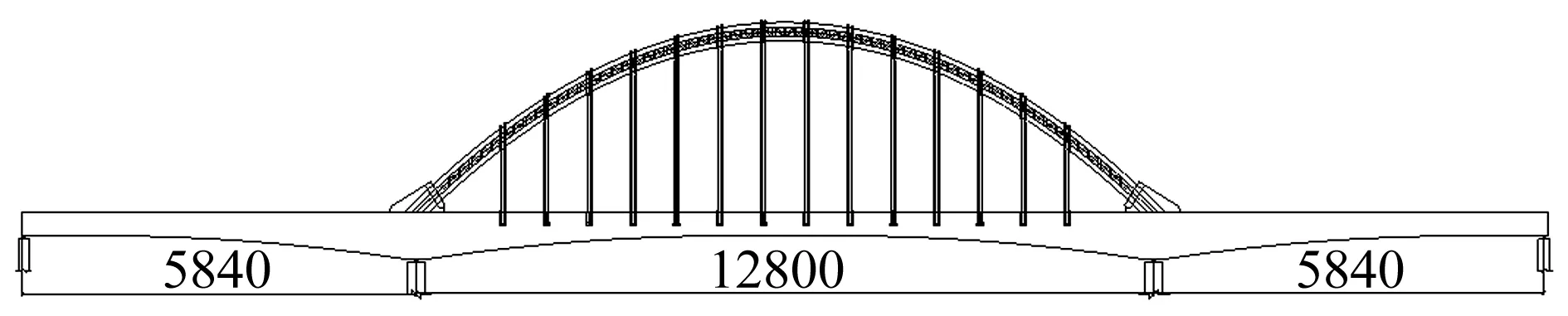
图2 杜坑特大桥立面布置图(单位:cm)

图3 现场测试测点布置图

对该桥施工完成后、通车前进行模态测试。对主梁与拱肋分别进行测试。为获得主梁竖向、横向模态特性，在主跨上下游每根吊杆处布置竖向测点，全桥共28个测点，进行7组测试；横向测点只布置在下游吊杆处，计7个测点，分3组测试。拱肋模态测试测点布置在上下游横撑位置，每处测点均布置横向、竖向传感器，测试分7组进行，各16测点。测点布置见图3。现场拱肋实际布点见图4。用大型通用有限元软件Ansys建立该桥空间杆系模型见图5。主梁用可模拟变截面Beam44单元；拱肋用适于联合截面的Beam189进行模拟；吊杆为只受拉Link10单元；拱肋横撑与主拱及吊杆与主梁以刚臂单元连接。模型修正参数设为：拱肋混凝土弹模Ec1，密度ρc1；拱肋钢管弹模Es1，密度ρs1；吊杆弹模Es2，密度ρs2；主梁混凝土弹模Ec2，密度ρc2；风撑刚臂弹模Eg1，吊杆刚臂弹模Eg2及二期恒载F。

图4 测点现场布置图

图5 结构有限元模型

用多参考点稳定图算法(M-NExT/ERA)[32]对测量数据进行模态参数识别，获得结构振型及频率，并与未修正有限元分析结果对比，见表2。按设计图纸结构参数建立有限元模型，获得未修正结果各阶频率与振型。计算结果与实测结果对比发现，现场实测前17阶结构模态并非有限元分析模型前17阶模态，而取有限元前25阶结果与实测结果进行振型与频率匹配方可获得17阶与实测模态相匹配的频率与振型(表2)。分析实测与有限元结果发现，未修正有限元模型17阶频率中有11阶误差超过10%，有限元模型与实际结构存在较大差异。表2中粗体为误差超10%频率。为说明修正模型与测试振型的关联度，计算测试振型与分析振型的MAC值。篇幅所限，仅给出拱肋1阶对称横弯、主梁1阶反对称横弯、主梁+拱肋1阶反对称竖弯与拱肋1阶扭转振型MAC值见表3。由表3看出，除拱肋1阶反对称竖弯外，其它振型MAC值均在0.95以上，说明分析振型与测试振型关联度较高，分析模态与测试模态匹配合理。

表2 实测结果与有限元计算结果对比 (单位: Hz)

表3 各模型修正方法振型MAC值

3.2.1 有限元模型修正过程

Kriging模型为基于小样本统计学习与预测的学习理论，被视为最优线性无偏估计，可在不影响结果精度前提下减少计算分析次数，提高计算效率。设结构设计参数为X～N(μ,σ)的正态分布，μ为各参数设计值，σ=μα为变量标准差，α为参数变异系数。取100组设计变量代入Ansys有限元模型，获得100组有限元分析结果。分别取拱肋横向振型对应频率、主梁拱肋竖向振型对应频率、主梁横向振型对应频率及拱肋扭转振型对应频率前2、3阶频率为训练样本，训练样本数100。以所得4组修正设计参数为基础，按修正结果精度赋予相应权值进行再次修正得最终修正结果。权值系数取和为1的随机数，并照精度顺序分配。修正后频率结果见表2，设计参数见表4。

用GA算法时，设结构参数为X～U(M(1-α)，M(1+α))的均匀分布，M为各参数设计值，α为各设计参数变异系数。建立Ansys与Matlab接口，GA算法在指定变量范围内生成设计参数，代入Ansys有限元模型计算获得结构频率与振型 (分析计算结果发现设计参数变化时结构振型阶次随之改变，需按Modal Assurance Criterion(MAC)方法[33]进行振型匹配以获得对应频率)。将实测频率与分析频率误差2范数作为目标函数，并映射为遗传算法的适应度函数。经40次迭代计算可得较理想结果。修正后频率结果见表2，修正后设计参数见表4。

BP神经网络优化初始权值与阈值矩阵对网络训练影响较大，故用GA算法对初始权值与阈值矩阵进行优化以改善神经网络质量。分析流程同Kriging模型，取300组设计变量，代入Ansys有限元模型，得300组有限元分析结果。一般情况下，训练样本数为连接权数的2～10倍为佳；为减少网络训练时间，分别取拱肋横向振型对应频率、主梁拱肋竖向振型对应频率、主梁横向振型对应频率及拱肋扭转振型对应频率前2、 3阶频率作为网络输入，设计参数为网络输出，以降低对训练样本总量要求。训练样本取270，测试样本取30。以所得4组修正设计参数为基础，按修正结果精度赋予相应权值进行二次修正，获得最终修正结果。权值系数取和为1的随机数，并按精度顺序分配。修正后频率结果见表2，修正后设计参数见表4。

3.2.2 结果比较与分析

表4为Kriging模型二次修正、GA算法及BP神经网络方法二次修正所得频率对比与修正后设计参数。表5为各模型修正方法误差范数比较。

表4 有限元模型设计参数修正结果

由表5看出，Kriging模型方法修正结果与各训练样本频率对应的修正模型频率误差最小，非对应修正模型频率精度略有不足。Kriging模型方法误差范数介于GA算法与BP神经网络方法之间，但修正后模型误差均在10%以下，且计算效率最高，耗时最少：对杜坑特大桥模型修正过程而言，Kriging模型方法计算时间约为BP神经网络方法的0.7倍，约为GA算法计算时间的0.2倍。基于Kriging模型的有限元模型修正能降低对样本数量依赖，可在满足计算精度的同时提高计算效率。GA算法修正后结果显示，仅有1阶频率误差超10%，修正结果得到较大程度改善，其误差2范数最小。仅定义足够多种群与遗传代数，遗传算法便能获得更高精度结果，但耗时会更长。分析BP神经网络方法修正结果发现，当取主梁、拱肋竖向振型对应频率为训练样本时所得修正模型误差2范数最小，而以主拱横向振型对应频率为训练样本的修正结果效果最差。与各训练样本频率对应的修正模型频率误差最小，非对应修正模型频率误差相对较大。相比GA算法与Kriging模型方法，BP神经网络方法计算精度最低，有3阶修正模态频率误差超10%，耗时介于GA算法与Kriging模型方法之间。

3.2.3 模型修正评价

评价模型修正方法及模型修正效果准则[34]为：

(1) 修正后有限元模型须能以一定精度预测有效频率范围内试验模态数据或频响函数。有效频率范围即参与有限元模型修正的频率范围；

(2) 修正后有限元模型须能预测有效频率范围之外的特征频率及振型；

(3) 修正后有限元模型须能获得其它除使用荷载工况外的频响函数；

(4)修正后有限元模型须能预测结果局部修改后模态数据或频响函数。局部修改可以是局部增加质量或改变边界条件而不涉及模型重新修正。

分析结果证明，本文三种方法模型修正结果均能满足准则1、2要求；准则3、4则需进一步实验及模型分析验证，此处暂不作讨论。

表5 各模型修正方法范数比较

图6 模型修正结果45°线匹配图

分别将试验结果与有限元计算结果作为横、纵坐标并示出匹配后各阶模态频率。若计算与试验结果吻合较好，则所有点应落在45°线上，否则说明模型误差较大[35]。以此绘频率匹配图。未修正、Kriging模型修正、GA方法修正及BP神经网络修正结果见图6。分析图6(a)、(b)，各修正方法所得频率未全部精确落在45°线上。整体而言，Kriging模型所得45°线匹配图各频率点分布更集中，较靠近45°线；BP神经网络所得频率点分布较分散。将GA算法、BP神经网络方法与Kriging模型方法二次修正所得结果集中于图6(c)的45°线匹配图中发现，所得曲线基本吻合，说明三种方法模型修正结果基本一致，亦即各修正模型均能反映结构的真实状况。

4 结 论

本文通过所提基于Kriging模型的有限元模型修正方法与GA算法及BP神经网络方法比较，并实例研究连续梁拱桥模型修正，结论如下：

(1) 模型修正结果精度依赖于实际测量结果精度，并与所用模型修正方法关系较大。

(2) 基于Kriging模型的有限元模型修正只要一定测量频率信息即可获得较高精度的修正模型，并能准确预测有效频率范围外结构模态特性。实际应用中可针对不同类型振型对应频率分别进行模型修正，并据修正结果进行二次修正获得更高精度修正模型。

(3) Kriging模型修正结果精度较高，且只需较少训练样本即可达到较高精度，耗时较少；GA算法修正模型精度最高，但需对有限元模型迭代求解修正，计算量较大，耗时最多；BP神经网络计算精度较低，且需较多训练样本，训练样本不足时模型修正结果精度低。

(4) 不考虑计算效率前提下，三种模型修正方法能获得较一致修正结果，表明三种方法均能用于此类复杂结构模型修正，并均具有较高计算精度。

[1] Mottershead J E, Friswell M I.Model updating in structural dynamics: a survey[J].Journal of Sound and Vibration, 1993, 167 (2): 347-375.

[2] Berman A, Flannelly W G.Theory of incomplete models of dynamic structures[J].AIAA, 1971, 9 (8): 1481-1487.

[3] Kabe A M.Stiffness matrix adjustment using mode data[J].AIAA, 1985, 23 (9): 1431-1436.

[4] 向锦武,周传荣,张阿周.基于建模误差位置识别的有限元模型修正方法[J].振动工程学报, 1997, 10 (1): 1-7.

XIANG Jin-wu, ZHOU Chuan-rong, ZHANG A-zhou.Modification of finite element model based on identified error locations[J].Journal of Vibration Engineering,1997,10 (1):1-7.

[5] Foster C D, Mottershead J E.Method for improving finite element models by using experimental data.Application and implications for vibration monitoring[J].International Journal of Mechanical Science, 1990, 32 (3): 191-203.

[6] Ting T.Design sensitivity analysis of structural frequency response[J].AIAA,Journal, 1993, 31(10): 1965-1967.

[7] Kye S W, Lin R M.Frequency selection method for FRF-based model updating[J].Journal of Sound and Vibration, 2004, 278 (1): 285-306.

[8] 李伟明, 洪嘉振.基于频响函数的模型修正方法[J].上海交通大学学报, 2011, 45 (10): 1455-1459.

LI Wei-ming, HONG Jia-zhen.Research on model updating method based on frequency response functions[J].Journal of Shanghai Jiaotong University, 2011, 45 (10): 1455-1459.

[9] Kirkpatric S, Gelatt C D, Vecchim P.Optimization by simulated annealing[J].Science,1983, 220 (4598): 671-680.

[10] Levin R I, Lieven N A J.Dynamic finite element model updating using simulated annealing and genetic algorithms[J].Mechanical Systems & Signal Processing,1998,12(1):91-120.

[11] Ziaei R S, Ewins D J.Finite element model updating of rotating structures using adaptive simulated annealing[C].// Proceedings of the 2002 International Conference on Noise and Vibration Engineering, 2002: 2281-2284.

[12] Atalla M J, Inman D J.On model updating using neural networks[J].Mechanical Systems & Signal Processing, 1998, 12 (1): 135-161.

[13] Levin R I, Lieven N A J.Dynamic finite element model updating using neural networks[J].Journal of Sound and Vibration, 1998, 210 (5): 593-607.

[14] Levin R I, Lieven N A J, Lowenbrug M H.Measuring and improving neural network generalization for model updating[J].Journal of Sound and Vibration, 2000, 238 (3): 401-424.

[15] Levin R I, Lieven N A J.Dynamic finite element model updating using simulated annealing and genetic algorithms[J].Journal of Sound and Vibration, 1998,12 (1): 91-120.

[16] 段雪平, 朱宏平.基于遗传算法的结构破损参数检测[J].工程力学, 2001 (A3): 422-426.

DUAN Xue-ping, ZHU Hong-ping.Structural damage parameters detection based on genetic algorithm[J].Engineering Mechanics, 2001(A3): 422-426.

[17] 闫桂荣, 段忠东, 欧进萍.遗传算法在结构有限元模型修正中的应用[J].哈尔滨工业大学学报,2007,39 (2):181-186.

YAN Gui-rong,DUAN Zhong-dong, OU Jin-ping.Application of genetic algorithm on structural finite element model updating[J].Journal of Harbin Institute of Technology,2007, 39(2): 181-186.

[18] Brownjohn J M W, Lee J, Cheong B.Dynamic performance of a curved cable-stayed bridge[J].Engineering Structure, 1999, 21 (11): 1015-1027.

[19] 范立础, 袁万城, 张启伟.悬索桥结构基于敏感性分析的动力有限元模型修正[J].土木工程学报, 2000, 33 (1): 9-14.

FAN Li-chu, YUAN Wan-cheng, ZHANG Qi-wei.Sensitivity-based FE model updating of a suspension bridge[J].China Civil Engineering Journal, 2000, 33 (1): 9-14.

[20] 张启伟.基于环境振动测量值的悬索桥结构动力模型修正[J].振动工程学报, 2002, 15 (1): 74-78.

ZHANG Qi-wei.Model updating of a suspension bridge using ambient vibration measurements[J].Journal of Vibration Engineering, 2002, 15 (1): 74-78.

[21] Hua H X, Sol H.On a statistical optimization method used in finite element model updating[J].Journal of Sound and Vibration, 2000, 231 (4): 1071-1078.

[22] Yuen K V, Lambros S, Katafygiotis B.Bayesian time-domain approach for modal updating using ambient data[J].Probabilistic Engineering Mechanics, 2001, 16 (3): 219-391.

[23] Wu J R, Li Q S.Finite element model updating for a high-rise structure based on ambient vibration measurements[J].Engineering Structures, 2004, 26 (7):979-990.

[24] 费庆国,张令弥,李爱群,等.基于统计分析技术的有限元模型修正研究[J].振动与冲击, 2005, 24 (3): 23-26.

FEI Qing-guo, ZHANG Ling-mi, LI Ai-quan, et al.Finite element model updating using statistics analysis[J].Journal of Vibration and Shock, 2005, 24 (3): 23-26.

[25] 韩芳, 钟冬望, 汪君.基于贝叶斯法的复杂有限元模型修正研究[J].振动与冲击, 2012, 31 (1): 39-43.

HAN Fang, ZHONG Dong-wang, WANG Jun.Complicated finite element model updating based on Bayesian method[J].Journal of Vibration and Shock, 2012, 31 (1): 39-43.

[26] Linda M, Tshilidzi M, Michale I F,et al.Model selection in finite element model updating using the bayesian evidence statistic[J].Mechanical Systems and Signal Processing, 2011, 25(7): 2399-2412.

[27] Jing D, Li X, Lei C, et al.Development and industrial application of soft sensors with online Bayesian model updating strategy[J].Journal of Process Control, 2013, 23(3): 317-325.

[28] Wackernagel H.Multivariate geo-statistics[M].Heidelberg: Springer-Verlag, 1995.

[29] Sacks J, Schiller S B, Welch W J.Designs for computer experiments[J].Technometrics, 1989, 31 (1): 41-47.

[30] Romero V J, Swiler L P, Giunta A A.Construction of response surfaces based on progressive-lattice-sampling experimental designs with application to uncertainty propagation[J].Structural Safety, 2004, 26 (2): 201-219.

[31] 贾布裕.组合梁斜拉桥的可靠度分析[D].广州:华南理工大学, 2011.

[32] 叶锡钧.基于环境激励的大型土木结构模态参数识别研究[D].广州:华南理工大学, 2012.

[33] Thomas G C, Clark R D．A modal test design strategy for model correlation[C].//Proc 13th International Modal Analysis Conference, New York：Union College, Schenectady, 1995: 927-933．

[34] Link M, Friswell M I.Working group 1: generation of validated structural dynamic models-results of a benchmark study utilizing the GARTEUR SM-AG19 test-bed[J].Mechanical Systems and Signal Processing,2003, 17 (1): 9-20.

[35] Ewins D J.Model validation: correlation for model updating[J].Sadhana, 2000, 25 (3): 221-234.