高尔夫收球机器人路径规划研究
,,,,
(中国科学技术大学精密机械与精密仪器系,安徽 合肥 230027)
LIAO Yuxiang,LU Siliang,ZHANG Haibin,ZHANG Shangbin,KONG Fanrang
(Department of Precision Machinery and Precision Instrumentation,University of Science and Technology of China,Hefei 230027,China)
高尔夫收球机器人路径规划研究
廖雨翔,陆思良,张海滨,张尚斌,孔凡让
(中国科学技术大学精密机械与精密仪器系,安徽 合肥 230027)
LIAOYuxiang,LUSiliang,ZHANGHaibin,ZHANGShangbin,KONGFanrang
(Department of Precision Machinery and Precision Instrumentation,University of Science and Technology of China,Hefei 230027,China)
机器人的路径规划问题一直是机器人研究的核心内容之一。在路径规划问题中,一般需要按照某一评价标准(如最短路径长度和最短行进时间等)来规划一条路径。提出一个能使工作效率(单位时间工作量)最高的评价标准,并将其应用于高尔夫捡球机器人的路径规划。基于该标准,并结合场地的特性和动态规划方法中的2个经典问题(01背包问题和数字金字塔问题),提出一个新的机器人路径规划算法。该算法按照一定的条件枚举多种可行的方案,通过计算最大单次工作量和路径长度得到每种方案的效率值,最后选择效率值最高的方案作为最优方案。
机器人;高尔夫球;路径规划;动态规划
0 引言
随着中国经济快速的发展,人民生活水平的快速提高,国民的健康意识在不断提升。高尔夫球作为休闲娱乐的一种方式,无疑将会越来越广地被人们所接受。通常来说,一个高尔夫练习场占地约为100亩,有60~80个击球位。每天从开馆到闭馆都会有络绎不绝的人前来练习高尔夫球,因此,回收打出去的高尔夫球成为了每一个高尔夫练习场所要完成的工作。
现阶段传统的高尔夫球场的捡球方式,主要都局限在人工驱动的领域,比如高尔夫捡球器[1-2]、两或三联捡球机等。但诸如此类的捡球设备,都是需要人工来操作进行,这就不可避免地带来了一个问题,即高尔夫球的回收工作与击打高尔夫球存在矛盾。在正常营业过程中,每一个击球位都会时刻不停击打出高速行进的高尔夫球,因此,如果在此时派人回收散落在球场上的高尔夫球,一定会对收球人员造成伤害,为此每一个高尔夫练习场都不得不在闭馆的时候才对高尔夫球进行回收工作,这就造成了效率低下及高昂的人工成本。智能高尔夫收球机器人[1]的出现,无疑在这一领域会有很大的应用价值,其不但可以解放人们辛劳烦琐的体力劳动,也可为高尔夫球场带来巨大的经济利益。
1 路径规划
高尔夫收球机器人定位为智能服务机器人,应用于高尔夫球场收集散落的高尔夫球。机器人通过自带的多传感综合定位以及相关的路径规划算法进行收球。
路径规划问题[3]是移动类型机器人的热点也是重点问题。对于高尔夫收球机器人的路径规划,主要解决3个问题,即使机器人能从初始点在球场中运动后回到初始点;用一定的算法使机器人能绕开障碍物;在完成以上任务的前提下,尽量优化机器人的工作效率。为了解决这些问题,还需要相对应的3个技术:传感技术;自定位技术;规划与决策。
高尔夫球场的障碍物较少,并且不是时刻变动的。算法应该充分利用环境信息的已知性,以优化工作效率为重点来规划路径。一个好的路径规划应满足以下指标[4]:
a.合理性。返回的任何路径都是合理的,或者说任何路径对控制机器人运动都是可执行的。
b.完备性。如果客观上存在一条从起点到达终点的无碰路径,该算法一定能找到;如果环境中没有路径可通行,会报告规划失败。
c.最优性。 算法规划的结果路径在某个测度(如时间、距离和能量消耗等)上是最优的。
d.实时性。 规划算法的复杂度(时间需求和存储需求等)能满足机器人运动的需要。
e.环境变化适应性。 算法具有适应环境动态改变的能力,随着环境改变,不必全部重新计算。
f.满足约束。 支持移动机器人运动时的完整性和非完整性运动约束。
2 动态规划[5-6]
2.1 01背包
现有一个背包,容积为m。n个物品,每个物品的体积为V[i]。请问,最多能放下多少个物品。
此问题的动态为f(i,j),表示第i个物品到第n个物品,这n-i+1个物品放在容积为j的空间里,最多能放下多少个。
状态转移方程为:
f(i,j)=max{f(i+1,j),f(i+1,j-V[i])+1}
(1)
2.2 数字金字塔
规定从最顶层走到最底层,每一步可沿左斜线向下或右斜线向下走。求解从最顶层走到最底层的一条路径,使得沿着该路径所经过的数字总和最大。
此问题的动态为f(i,j),表示从点(i,j)往下走能得到的数字最大总和。d(i,j)表示点(i,j)的数值。
状态转移方程为:
f(i,j)= max {f(i+1,j),f(i+1,j+1)}+
d(i,j)
(2)
2.3 动态规划的计算方法
动态规划的计算方法依赖于状态与状态转移方程。以01背包为例,问题的动态为f(i,j),背包的总容量为m。f(1,m)就是01背包问题的解。利用式(1)将问题转换求f(2,m)与f(2,m-V[i])的值,算法的时间复杂度为o(2n),这个时间复杂度是不能接受的。实际上对于任一个状态f(i,j),它都是独立的,在状态转移过程中,会重复访问某一个状态f(p,q),当访问过一次后,将其值记录,待再次访问时,可以直接调用其值。而f(i,j)的状态只有n×m个,所以算法的时间复杂度实际为o(n×m)。
3 动态规划在机器人中的应用
3.1 路径规划方法描述
高尔夫球场中有几种区域是不能通行的,即洼地,周围有栏杆保护,不可通行;指示牌或广告牌,不可触碰。如果S为机器人起始点状态;X为当前机器人的状态;M为网格地图表示的环境地图;T为机器人单次工作的总量。那么提出的路径规划方法可表示为:
a.枚举一个目标点G,基于环境信息M,规划出从S到G的全局最优路径L和此路径的工作量TL。
b.基于M和L,得到一个新的环境信息ML(L路径上点的值变为0)。
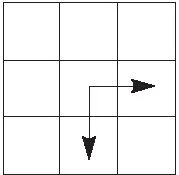
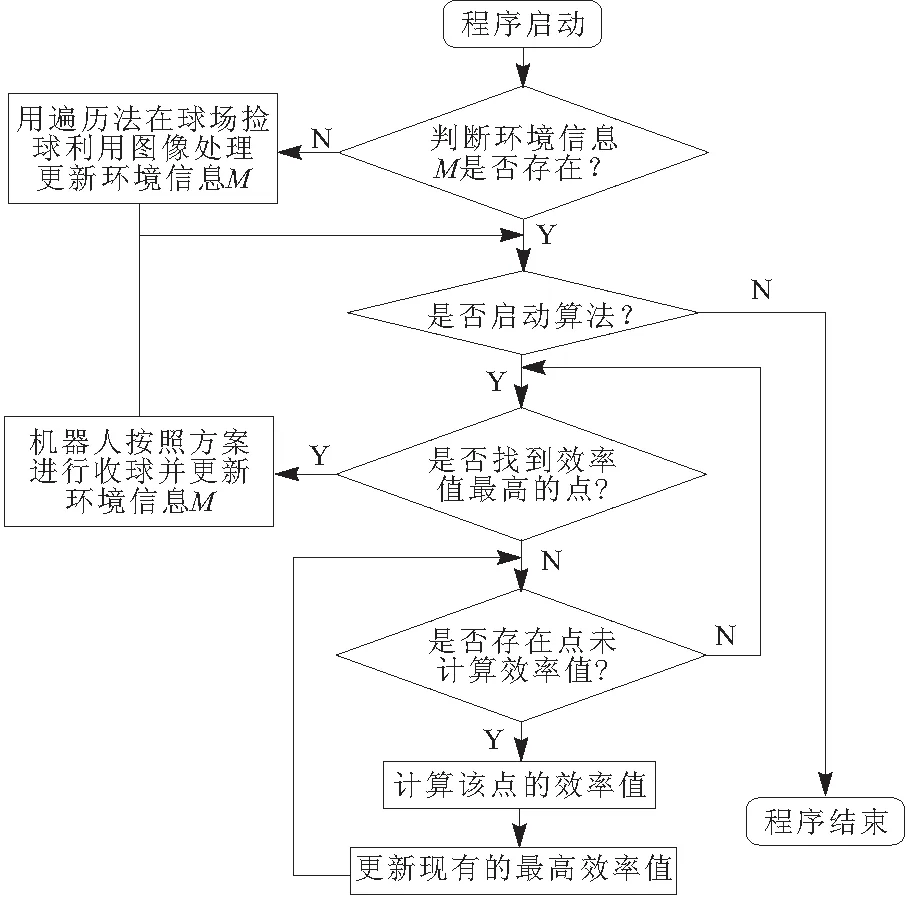
c.基于环境信息ML,规划出从G到S的全局最优路径LB和此路径的工作量TB,使得TB+TL d.计算效率值EG,记TG=TL+TB,记LG为路径L和LB的总长度,则EG=TG/LG。 e.找出效率值最高的点Gmax和路径Lmax,令X=Gmax,并按照路径Lmax执行。 f.按照传感器信息和路径Lmax信息更新M,跳转到a步。 3.2 动态规划部分算法描述 高尔夫球场上仅有一些简单的障碍物,规定机器人由出发点S向目标点G行进的过程中,机器人只按照图 1中所示的2种方案前进(在网格中,只能向上或者向左移动,参照2.2节数字金字塔)。此方法在一般的机器人移动问题中是不可取的,如图 2所示(斜线为此方法不可到达的地方)。但是在如此宽阔的高尔夫球场中,几乎是不存在此类陷阱区域,仅有极其特殊的情况会出现图 2情况。如果存在,可以先通过宽度优先搜索找到这些地方,在算法中对这些节点进行特殊处理(测试场地不包括图 2中斜线所示陷阱区域,系统算法不包含对此类节点的特殊处理)。 图1 行进方案 图2 特殊情况 定义一个动态f1(i,j)表示从出发点S(1,1)到目标点G(i,j)的最大工作量。由上述行进方案和式(2)可得如下状态转移方程,即 f1(i,j)=max{f1(i-1,j),f1(i,j-1)}+m(i,j) (3) m(i,j)为环境信息M中点(i,j)的值。将G点代入式(3)可得f1(G)的值(也就是路径的工作量TL)和路径L。 规定机器人由目标点G向出发点S行进的过程中,机器人只按照图 3所示2种方案前进。此方法必然有一条路径能到达S(按照f1(i,j)所求路径L返回)。 图3 由目标点向出发点行进方案演示 定义一个动态f2(i,j),表示从点G(i,j)出发到出发点S(1,1)的最大工作量。参照式(3),基于环境信息ML,规划出从G到S的全局最优路径LB和此路径的工作量TB,使得TB+TL f2(i,j,k)=max {f2(i-1,j,k1)+ml(i-1,j), f2(i,j-1,k2)+ml(i,j-1)} (4) ml(i,j)为环境信息ML中点(i,j)的值;k1=k-ml(i-1,j),k2=k-ml(i,j-1)。将G点和f2(G)代入式(4),可得TB和路径LB。 综上可得效率值EG为: (5) 3.3 整体算法描述 算法流程如图 4所示。 图4 算法流程 算法中,均依赖环境信息M运算,若环境信息M不能建立并及时更新,算法就会失效。机器人配置有摄像头,拍摄图像后做图像二值化处理。但是单个摄像头拍摄图像不能获得深度信息,并不能有效地更新环境信息M,在实际测试中,不能满足算法的要求,必须引进其他技术进行改进。双目视觉技术模仿人的双眼,利用2个摄像机同时采集同一场景的图像,由于2台摄像机位置不同,采集的图像存在视差,利用这一视差可以直接获取空间物体的深度信息[7-8],使得算法可以有效地更新环境信息M。 因测试球场范围较大,按照一定规格划分为二维网格后运算量也较大,所以算法仿真过程中模拟一个小的二维图,如图 5所示。仿真过程中只对其中的几个方案计算效率值,并不直接求出效率值最高的方案。 图5中白色区域为可通行区域,黑色区域为洼地、指示牌或广告牌等不可通行区域,右下角S代表机器人出发位置,其余数值代表环境信息M中点(i,j)的值。 图5 环境信息 枚举点G,这里取2个点来计算EG,如图 6所示。 图6 枚举方案 设单次工作量T=50。分别将G1、G2带入式(3),得f1(G1)=28,f2(G2)=48。分别在路径LG1与LG2下的ML如图 7所示。LG1与LG2分别为图 7所示虚线部分。 图7 路径LG1和LG2 分别将G1、k1=T-f1(G1)=22与G2、k2=T-f2(G2)=2代入式(4),可得f2(G1,k1)=10,f2(G2,k2)=1。G1、G2下的LB如图 8所示实线部分。 图8 G1、G2下的路径LB 分别求出TG1、LG1与TG2、LG2,得: (6) (7) 由式(5)~式(7)得: (8) 由式(8)得出结论,选择G1方案的效率比选择G2方案的效率要高。 路径规划的方法有很多,基于路径规划的特性,动态规划实际上是不适合路径规划的。但是在特殊情况下,引入动态规划是可以达到解决问题的目的。通过简单介绍动态规划的一些基本案例,从动态规划得到的经验中加以结合,提出了一种基于动态规划的以工作效率值为评价标准的高尔夫捡球机器人路径规划算法,此算法能有效地提高高尔夫收球机器人的工作效率。 但是,还存在2个需要改进的地方,一是,图 2中斜线所示陷阱区域,虽然出现几率极低并且出现后也对算法影响不大,但是也必须给出一个算法来处理这特殊情况;二是,虽然提出了利用双目视觉来获取空间深度信息以便更新环境信息M,但是具体的方法仍需要探讨。 [1] Pereira N,Ribeiro F,Lopes G,et al.Autonomous golf ball picking robot design and development[J].Industrial Robot:An International Journal,2012,39(6):541-550. [2] 张韬懿,王田苗,吴耀,等.全地形无人车的设计与实现[J].机器人,2013,35(6):657-664 [3] Ge S S,Cui Y J.New potential functions for mobile robot path planning[J].IEEE Transactions on Robotics and Automation,2000,16(5):615-620. [4] 曲道奎,杜振军,徐殿国,等.移动机器人路径规划方法研究[J].机器人,2008,30(2):97-101. [5] 李端,钱富才,李力,等.动态规划问题研究[J].系统工程理论与实践,2007(8):56-64. [6] Bertsekas D P.Dynamic programming and optimal control[M].Belmont,MA:Athena Scientific,1995. [7] 邱河波.基于DSP的移动机器人双目视觉技术研究[D].成都:电子科技大学,2013. [8] 祝琨,杨唐文,阮秋琦,等.基于双目视觉的运动物体实时跟踪与测距[J].机器人,2009,31(4):327-334. Research on Path Planning for a Golf Ball Picking Robot Path planning problem for a robot is one of the crucial contents in robotics research.In the path planning problem,a criterion (e.g.,shortest path length,shortest travel time,etc.) is required to plan a path for the robot.In this study,we propose a criterion that can maximize the work efficiency (highest workload in unit time) and apply this criterion to the path planning of a golf ball picking robot.Subsequently,we proposed a new path planning algorithm by considering both the characteristics of the golf course and the two classical problems of the dynamic programming (the 01 knapsack problem and the digital pyramid problem).The proposed algorithm enumerates several solutions according to the certain conditions,and then calculates the corresponding efficiency values by computing the maximal workloads and the maximal path lengths,and finally achieves the optimal solution by selecting the maximal efficiency value. robot; golf ball; path planning; dynamic programming 2014-08-12 TP242.6 A 1001-2257(2014)12-0077-04 廖雨翔(1990-),男,四川绵阳人,硕士研究生,研究方向为智能控制,机器人。

4 仿真过程与结果




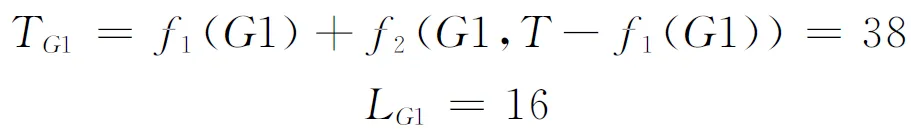
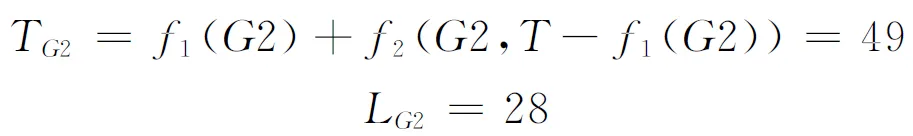

5 结束语

