特定频域特性的风模型研究
,,,
(1.许昌许继风电科技有限公司,河南 许昌 461000;2.许继集团有限公司,河南 许昌 461000)
特定频域特性的风模型研究
陈娜娜1,卢晓光1,霍富强2,王萌1
(1.许昌许继风电科技有限公司,河南 许昌 461000;2.许继集团有限公司,河南 许昌 461000)
为了保证风力机设计过程中所需要载荷计算的准确性,以确保风力机各零部件的动力学分析和寿命计算,需要在实验室中得到与自然风具有相同数学特性的风速序列。对Kaimal功率谱密度函数进行逆傅里叶变换得到离散时间序列,通过对该序列的频谱特性与某风场实测风速序列的频谱特性进行对比分析,结果表明,该方法能够得到具有特定功率谱密度和随机特性的风速时间序列。
风速;时间序列;功率谱密度;傅里叶变换
0 引言
近年来,随着风力发电技术的发展,对风机运行时所处环境的分析和对各种载荷进行精准的计算显得尤为重要。而大气边界层内的风特性是决定上述计算的重要因素,对特定风场风资源的研究被广泛的关注。
作为风力发电机的输入源,风特性对于风力发电系统有直接的影响。因此,在实验室中若要对风力风电系统进行载荷计算和动态模拟等,首先就要计算出与实际风速具有相同数学特性的风速序列,从而能够对风速的变化进行模拟。因风速序列本身具有时间、空间上的随机性和复杂性,众多类似的文献研究分析表明,Kaimal谱的特性与自然界中实测风速序列所呈现的随机特性较为吻合[1]。因此,通过对Kaimal谱进行傅里叶反变换所计算出的离散风速序列的功率谱,能够与实测风速时间序列功率谱保持基本一致,那么就证明通过傅里叶反变换所得到的风速序列,能够较为准确地表现出风速的变化过程,可以反映出特定风场风速的客观变化的信息和行为特征[2-6]。这样生成的时间序列拥有与历史风速数据具有相似的数学特性,能够为实验室的仿真研究提供基础,进而做到优化和完善各系统的实验模型。
1 湍流风特性
风湍流是指10 min内平均风速的随机变化。风湍流模型应包括风速变化、风向变化和旋转采样的影响。湍流风速的3个矢量分别定义如下[7],即纵向分量即沿着平均风速方向;横向分量即在水平面内,垂直于纵向分量;竖向分量即垂直于纵向分量和横向分量。
对于正常湍流模型,湍流标准偏差特性σ1,在给定轮毂高度的风速应按概率分布为90%分位点值给出。对标准等级的风力发电机组,随机风湍流模型速度场应满足下列要求。
纵向风速分量的标准差特性值σ1为:
σ1=I15(0.75V10min+b)
(1)
b=5.6 m/s;I15是风速为15 m/s时的湍流强度特性值;V10min为10 min平均风速,假定标准偏差不随离地面高度变化。平均风速方向的垂直分量应具有以下最小标准偏差,即横向分量σ2≥0.7σ1,竖向分量σ3≥0.5σ1。
在惯性子区间,3个正交分量的功率密度分别为S1(f)、S2(f)、S3(f),作为频率f的函数应逼近下列渐近线形式,即
S1(f)=0.05(σ1)2(L/V10min)-2/3f-5/3
(2)
S2(f)=S3(f)=4/3×S1(f)
(3)
L为纵向湍流尺度参数。
目前,满足上述要求的自然风湍流模型有很多,常用的有Kaimal谱、Von-karman谱和Davenport谱。Kaimal谱已经被广泛接受且满足上述湍流模型的要求,因此,以Kaimal谱作为时间序列拟合的目标[8-9],即

(4)
I=σ/V10 min为湍流强度;f为无量纲频率;L为与高度相关的湍流长度尺度,当离地面高度h小于30 m时,L=20×h,当离地面高度h大于30 m时,L=600×h。在轮毂高度,平均风速为13 m/s,湍流强度特性值为0.14的Kaimal谱曲线如图1所示。

图1 平均风速13 m/s的Kaimal谱曲线
2 功率谱密度
位于大气边界的自然风一般为湍流风,湍流风在时间、空间上都具有复杂性和随机性,表明气流不稳定,该气流随机周期的变化范围从零点几秒到几分钟,因此,需要用随机过程的方法才能描述湍流风[9]。
某风场所测到的实际风速序列可作为随机过程的研究对象,风速序列X(t)即是该过程的随机样本。对于离散的风速序列X(t)不需要复杂的时域分析,可以通过傅里叶变换进行频域分析。同样随机过程也可以利用傅里叶变换来分析其频谱结构。对随机过程进行傅里叶变换可以得到其傅里叶谱F(ω),反之,对傅里叶谱F(ω)也可以通过傅里叶逆变换得到相应的随机过程。
傅里叶谱包含傅里叶幅值谱与傅里叶相位谱,是从2个不同的方面对随机过程的频谱进行描述。经典的傅里叶变换方式,由随机样本时程给出随机傅里叶谱样本,进而给出其概率描述,但是,随机过程的样本函数一般不满足傅里叶变换绝对可积条件,而且随机过程的样本函数往往并不具有确定的形状,很难解释其物理意义,因此,不能直接对随机过程进行谱分解。然而随机过程的功率谱S(ω)等于该序列的傅里叶变换幅值谱平方的平均值,即[9-10]
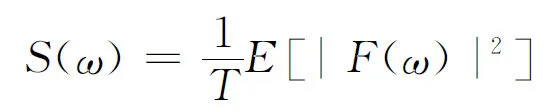
(5)
T为样本的持续时间;|F(ω)|为样本傅里叶变换幅值谱。从式(5)看出,工程上可以用功率谱表示傅里叶幅值谱。通常,工程中应用的功率谱函数往往具有一定的物理意义,因此,可以分析它的功率谱。
S(ω)是从频域的角度描述X(t)统计特性的重要数字特征,它表征了随机过程的能量分布,但是S(ω)仅表示X(t)的平均功率在频域上的分布情况,不包括X(t)的相位信息。
对于平稳随机过程X(t),如果相关函数RX(τ)满足[11-13]:
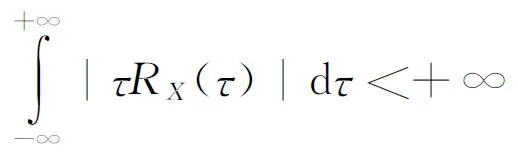
(6)
(7)
即功率谱密度为相关函数的傅里叶变换。如果随机过程的平均功率是有限的,则有:
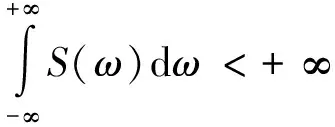
(8)
此时随机过程X(t)的自相关函数为:
(9)
在满足式(6)和式(8)的条件下,平稳随机过程的相关函数和功率谱之间是傅里叶变换对的关系,这就是著名的维纳-辛钦定理。
式(8)的条件一般都是满足的,而式(6)的条件要求随机过程的均值为零,且RX(τ)中不能含周期分量,含有直流分量和周期分量的随机过程是很多的,这就限制了定理的应用。但如果引入σ函数,那么就可不受此条件的限制,即对于平稳随机过程,认为式(9)总是成立的。
现有某风场采集的实际风速数据,平均风速为13 m/s,采样周期为0.05 s,总采样时间为600 s,其风速序列曲线如图2所示。

图2 某风场实际风速时间序列曲线
对该风速序列进行功率谱密度分析,可以得到如图3所示的频谱分布。
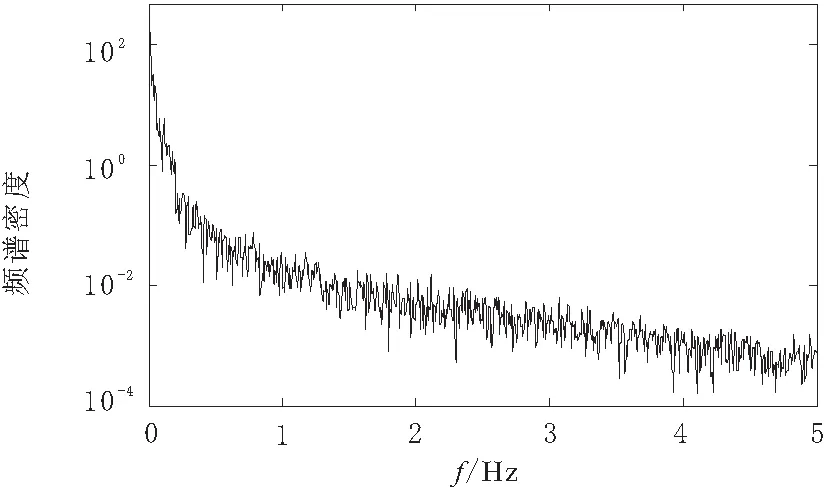
图3 某风场实测风速序列的频谱
3 拟合风速序列
某风场一风速仪以fs=1/Δt的采样频率测试出该风场的实际风速ui,其中i=1,…,N,Δt是指相邻2个采样点间的时间,相应的采样时间t=1×Δt,2×Δt,…,N×Δt,采样总时间T=Δt×N。对于具有时间和空间特性的风速时间序列,可以用离散傅里叶变换来描述,即
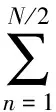
(10)

(11)
(12)
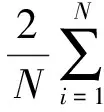
(13)
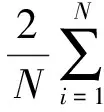
(14)
(15)
由式(10)可得,随机序列的方差为:
(16)
(17)
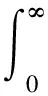
(18)
f是频率,将式(18)离散化可得:
(19)
由式(14)和式(16)可得,随机序列的功率谱密度函数S(f)为:
(20)
实际随机风速序列u1…uN傅里叶变换的系数和该序列的功率谱密度函数,分别由式(13)、式(14)式和(20)决定,这种方法称为离散傅里叶变换。相反,可通过逆傅里叶逆变换,来构造具有一定功率谱密度函数和随机特性的时间序列。
风速序列模型采用平均风速分量与湍流分量相叠加的风速模型。这种模型中,平均风速可在数分钟至数10 min的时间尺度内保持不变,风速的变化由湍流分量给出。因此,风速序列模型为:

(21)
即
(22)
根据实际的实验需要,为了能够使所计算出的风速序列具有式(4)所示功率谱特性,采用对式(4)所给出的功率谱函数进行逆傅里叶变换。由式(5)知,随机序列功率谱S(ω)等于该序列的傅里叶变换幅值谱平方的平均值,因此,式(22)可变换为:
(23)
t=i×Δti=1,…,N
通过式(23)可以计算出符合Kaimal谱刻画的离散时间序列。计算所得的风速时间序列和其功率谱密度分别如图4~图5所示。
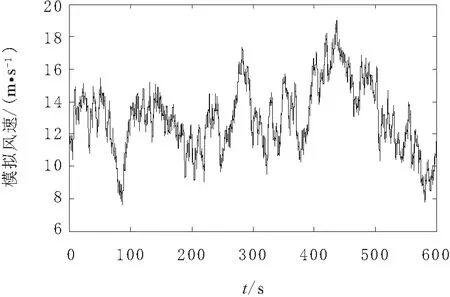
图4 模拟风速时间序列曲线
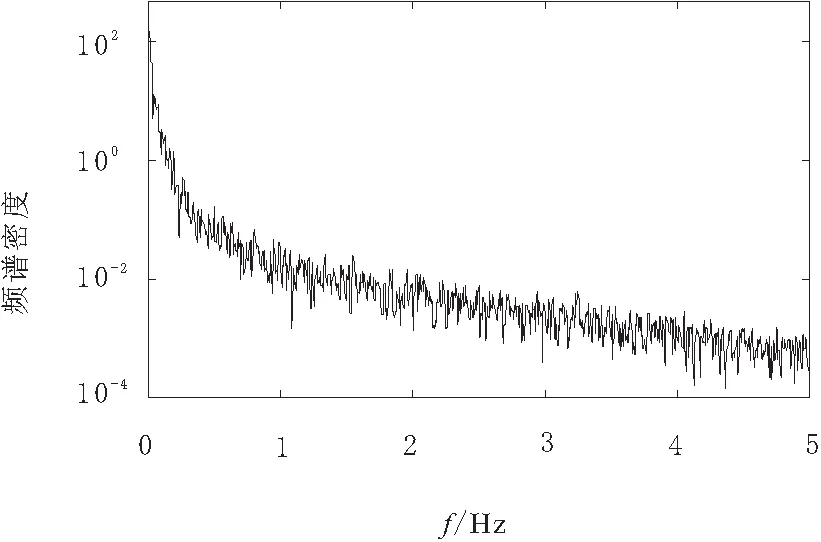
图5 模拟风速频谱特性
比较图3和图5的频谱特性可知,现场采集实时风速和模拟风速的频率特性是一致的。
4 结束语
通过理论分析以及图3和图5所呈现出的频率特性可得出,由傅里叶反变换所计算出的风速序列,其功率密度函数与风场实际采集的风速序列的功率谱密度基本一致,具有相同的数学特性。通过算法能够在实验室中,方便地得到与实际风速序列具有相同数学特性的风速序列,从而满足实验室中风力发电项目中各系统的仿真需求。同时,在频域中利用傅里叶变换,提高了计算效率,也体现了算法的优越性。
[1] 李东东,陈陈.风力发电系统动态仿真的风速模型[J].中国机电工程学报,2005,25(21):41-44.
[2] 张建忠,程明.风力发电随机风速时间序列生成方法分析与评价[J].风能,2012(1):58-61
[3] 修春波,任晓,李艳晴,等.基于卡尔曼滤波的风速序列短期预测方法[J].电工技术学报,2014,29(2):253-259.
[4] 屈晓栋.风电场风速预测模型研究和实现[D].无锡:江南大学.2009.
[5] 曾庆基.风电功率时间序列模拟生成方法研究[D].哈尔滨:哈尔滨工业大学,2013.
[6] 杨军.风电机组动态分析适用风速模型[J].西南科技大学学报,2010,25(1):39-44.
[7] 风力发电机组规范[S].北京:中国船级社,2008.
[8] Martin O L,Hansen.Aerodynamics of wind turbines[M].UK and USA:Second Edition Ppublished by Earthscan,2008.
[9] 克莱斯·迪尔比耶.结构风荷载作用[M].薛素铎,李雄彦,译.北京:中国建筑工业出版社,2006.
[10] 李杰,张琳琳.脉动风速功率谱与随机Fourier幅值谱的关系研究[J].防灾减灾工程学报,2004,24(4):363-369.
[11] 徐进军,付孙钟.频谱分析在周期拟合中的应用[J].测绘信息与工程,2001(3):20-22.
[12] 丁明,张立军,吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备,2005,25(8):32-34.
[13] 罗鹏飞,张文明.随机信号分析与处理[M].北京:清华大学出版社,2006.
Research on Wind Model of the Specific Frequency Domain Characteristics
CHENNana1,LUXiaoguang1,HUOFuqiang2,WANGMeng1
(1.XJ-Wind Power Technology Company,Xuchang 461000 China;2.XJ Group Corporation,Xuchang 461000 China)
In order to ensure the accuracy of the required load calculation in design processing, and the dynamic analysis and the life calculation of components of the wind turbine, it need to get the series with natural wind characteristics in laboratory.The article obtain discrete time series by the inverse Fourier transform of Kaimal power spectral density function.By comparing the spectral characteristics of the sequence with the spectral characteristics of the measured, the results show that this method can obtain wind speed time series with certain specific power spectral density and random characteristics.
wind speed; time series; power spectral density; Fourier transform
2014-09-23
TK81
A
1001-2257(2014)12-0043-04
陈娜娜(1987-),女,河南济源人,硕士,研究方向为风电储能系统的调度控制和策略;卢晓光(1983-),男,河南许昌人,硕士,工程师,研究方向为机电一体化技术。

