不锈钢管弯曲成形回弹预测研究
,, ,
(1.中航飞机股份有限公司西安飞机分公司,陕西 西安 710089;2.西北工业大学机电学院,陕西 西安 710072)
不锈钢管弯曲成形回弹预测研究
王天立1,梁正龙2,张深2,吴建军2
(1.中航飞机股份有限公司西安飞机分公司,陕西 西安 710089;2.西北工业大学机电学院,陕西 西安 710072)
使用有限元分析软件ABAQUS,建立了有效的不锈钢管材弯曲回弹有限元仿真模型,运用虚拟正交试验方法,研究了弯曲角度、直径、壁厚、助推速度以及弯曲模与管壁之间的摩擦系数,对弯曲回弹的影响,最后分别用线性回归和神经网络,建立回弹角度与上述参数间的定量关系。结果表明,回弹角随着弯曲角度的增大而增大,且呈现出明显的线性关系;与回弹角度相比,直径、壁厚、助推速度以及摩擦系数对回弹角的影响较小;神经网络更能准确地对回弹角与上述参数间的关系进行预测。
不锈钢;回弹;虚拟正交试验;线性回归;神经网络
0 引言
不锈钢管由于具有较好的耐腐蚀性能,被广泛应用于航空航天、汽车船舶和石油化工等领域。在管材弯曲成形过程中,由于存在弹性变形和塑性变形区域中的弹性变形,卸载后将不可避免的产生回弹,严重影响弯管零件的制造和装配精度。因此,有必要对管材弯曲回弹预测进行研究,从而实现对生产过程中回弹的精确控制。
尽管许多学者针对不锈钢管弯曲回弹做了大量研究[1-4],并取得了一定的成果,但是,现有方法在提高回弹预测精度以及减少所用时间方面还有待进一步提升。以不锈钢管材的数控绕弯成形回弹预测为研究对象,使用有限元软件ABAQUS,基于虚拟正交试验,分别运用线性回归方法和BP神经网络对回弹进行预测研究。
1 回弹模型建立
1.1 材料模型
研究对象为不锈钢(0Cr18Ni9)管材,针对20 mm×1 mm(外径×壁厚)的不锈钢管,依据国标GB/T 228.1-2010 《金属材料拉伸试验第1部分:室温试验方法》设计拉伸试样,采用CSS-44100电子万能试验机进行单向拉试验,拉伸速度为1 mm/min,采用幂指数硬化模型σ=kεn对塑性阶段的应力应变关系进行拟合,材料力学性能参数如表1所示。
表1 0Cr18Ni9不锈钢管材力学性能参数

E/GPaμδu/(%)σs/MPaσb/MPaK/MPan1700 3643 22606305050 37
E为弹性模量;μ为泊松比;δu为断后延伸率;σs为屈服极限;σb为强度极限;K为硬化系数;n为硬化指数。
1.2 仿真模型
回弹作为仿真模拟过程中最后一步,成形仿真过程中的任何误差都会累积到回弹阶段,因此,建立精确的有限元数值模拟模型是准确预测回弹的基础。
首先运用有限元分析软件ABAQUS/Explicit平台进行绕弯成形 - 抽芯过程仿真计算;然后运用ABAQUS/Standard平台进行回弹计算。鉴于0Cr18Ni9不锈钢管材没有明显的各向异性,选用MISSES屈服准则描述材料的屈服行为;采用具有沙漏控制和减缩积分属性的C3D8R实体单元对管子建模,壁厚方向设置4个单元,同时对管子采用分段加密的方式划分网格;采用刚性四边形单元R3D4描述模具型面;管子外壁与模具的接触使用运动接触算法,而内壁与模具的接触使用罚接触算法,使用库伦摩擦模型描述接触面之间的接触行为;选用位移/速度边界条件描述成形过程中模具与管子的运动;为了同时兼顾计算精度与计算效率,质量缩放系数大小设置为2 500。
1.3 回弹角描述
成形模拟完成后进行回弹计算,固定管子的后端,让前端自由回弹,回弹角度用回弹前后的角度差表示,如图1所示。
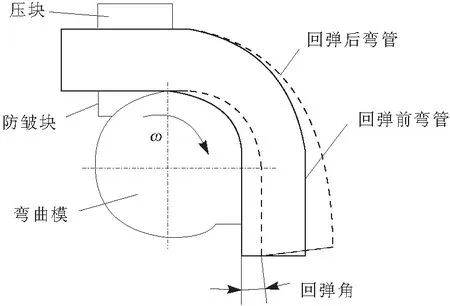
图1 弯管回弹角度
1.4 仿真模型实验验证
使用美国ERTON LEONARD公司生产的VB300HP型数控弯管机进行弯管试验。在工艺参数相同的条件下,针对20 mm×1 mm(外径× 壁厚) 的不锈钢管,仿真与实验结果对比如表2所示。由表2可知,仿真模拟模型可靠有效。
表2 仿真与实验结果对比

弯曲角度/(°)仿真回弹角/(°)真实回弹角/(°)误差/%301 21 414 3902 12 29 01202 83 19 67
2 虚拟正交试验
管材弯曲成形过程是一个多参数影响、多模具约束的复杂塑性成形过程[5],合理的设定成形参数,对管材成形回弹控制至关重要。而现有的研究大多集中在定性分析,很少有研究给出回弹角的定量计算公式。故将正交试验设计与有限元数值模拟相结合,得到了不同成形参数组合对应的回弹角度,为建立上述定量关系提供数据支持。
在众多成形工艺参数中,选取管径、壁厚、弯曲角度、弯曲模与管壁之间的摩擦系数以助推比(真实助推速度与最外侧切线速度的比值)作为正交试验的5个因素,每个因素取4个水平,建立正交试验表并进行仿真实验。最后将5个因素的4个平均回弹角度表示在一张图上,如图2所示。从图2可以发现,弯曲角度对回弹角度的影响最大,随着弯曲角度的增大,回弹角也呈增加的趋势;与之相比,其他参数对回弹的影响较小,基本在0.2°的范围内浮动。
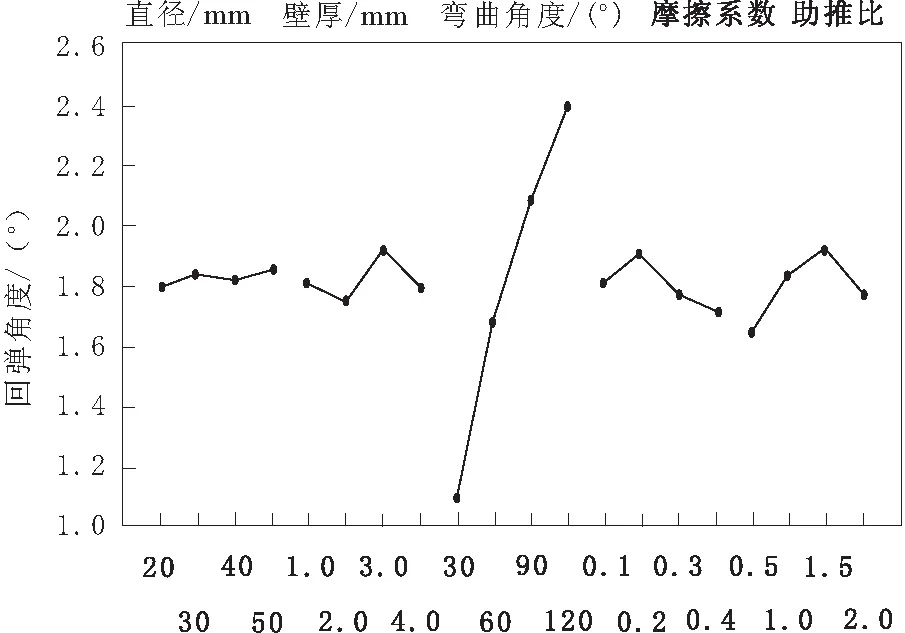
图2 回弹角与5个因素关系
3 线性回归与神经网络组合预测
3.1 线性回归
为了确定上述因素对回弹角度的影响,建立其与回弹角度大小之间的数值关系,基于虚拟正交试验,利用SPSS软件,对上述5个因素与回弹角度之间的关系,使用逐步法进行线性回归处理[6],最终得到回归方程为:
a=0.797+0.014θ
分析上式可以发现,最终进入回归方程的因素只有弯曲角度,由逐步法线性回归理论可知,直径、壁厚、弯曲模与管壁之间的摩擦系数以及助推比对回弹角度的影响较小,与图2反映的结果相符合。
为了验证回归模型的有效性,对回归方程进行方差分析,结果如表3所示。
表3 回归方程ANOVA分析结果

模型平方和自由度均方FSig1回归3 40713 407230 9320 000残差0 207140 015总计3 61415
回归方程的显著性检验结果表明,回归平方和为3.407,残差平方和为0.207,总平方和为3.614,对应的F统计量的值为230.932,显著性水平小于0.05,因此,可以认为建立的回归模型有效。对回归系数进行显著性检验,结果表4所示。
表4 回归系数表
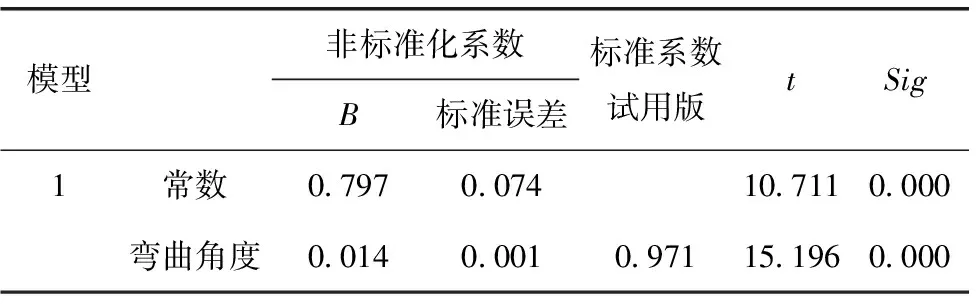
模型非标准化系数B标准误差标准系数试用版tSig1常数0 7970 07410 7110 000弯曲角度0 0140 0010 97115 1960 000
由表4可知,回归系数B的估计值为0.014,标准误差为0.001,标准化的回归系数为0.971,回归系数显著性检验t统计量的值为15.196,对应显著性水平小于0.05,可以认为方程显著。
对回归方程的方差分析以及对回归系数的显著性检验均发现,所建立的回归方程显著,因此,可以用来进行回弹预测。将回归预测值与仿真结果进行对比,结果如表5所示,其中,

100%

100%
表5 回归预测与仿真结果对比

弯曲角度/(°)回归预测值/(°)仿真结果均值/(°)均值误差/%最大误差/%301 2171 1406 3310 85601 6371 6963 607 60902 0572 0941 804 861202 4772 3833 798 24
从表5的比较可以发现,回归模型对回弹角度的预测值与仿真结果相比较,均值误差不超过6.5%,最大误差不超过11%,回归预测值与仿真结果比较接近。
3.2 神经网络预测
人工神经网络由于具有自组织、自学习和自适应等一系列的优点,在模式识别与图像处理,控制与优化,预测与管理等领域获得了广泛的应用,解决了许多传统方法难以解决的问题[7]。
采用双层前向反馈神经网络预测模型,隐层采用Sigmoid传递函数,输出层采用purelin传递函数,训练函数选用trainlm,最终建立的网络结构,如图3所示。

图3 神经网络结构
神经网络必须要有大量的训练样本进行训练才能更好体现其非线性映射能力,因此,对虚拟正交试验结果进行分组处理,1,2,5,8号实验作为验证试验,其余实验作为训练样本并对网络进行训练。最后将神经网络预测结果与仿真结果进行对比,结果如表6所示。
表6 神经网络预测与仿真结果对比

试验编号 弯曲角度/(°) 仿真结果值/(°) 神经网络预测误差/%1601 6621 650 722902 1572 2574 645301 0851 155 9981202 6672 7974 87
通过表6的对比可以看出,神经网络的预测结果和仿真结果比较接近,最大误差为6.0%,预测结果与仿真结果吻合良好。
4 结束语
基于ABAQUS平台建立了虚拟正交试验所需的不锈钢管弯曲成形及回弹的有限元仿真模型,并通过实验验证了模型的可靠性。与弯曲角度对不锈钢管回弹影响相比,直径、壁厚、助推比以及弯曲模与管壁之间的摩擦系数对回弹角度的影响较小,且弯曲角度与回弹角度之间呈现出明显的线性递增关系。逐步线性回归与神经网络均能对回弹进行快速准确的预测,但BP神经网络由于综合了直径、壁厚、助推比以及弯曲模与管壁之间的摩擦系数等对回弹的影响,与逐步线性回归预测相比,预测精度更高。
[1] 贾美慧,唐承统.不锈钢管材弯曲成形回弹预测模型研究[J].北京理工大学学报,2012,32(9):910-914.
[3] Daxin E,Liu Yafei.Springback and time-dependent springback of 1Cr18Ni9Ti stainless steel tubes under bending[J].Materials and Design ,2010(31):1256-1261.
[4] 王泽康,杨合,李恒,等.大口径 316L 不锈钢管数控弯曲回弹规律研究[J].材料科学与工艺,2012,20(4):49-54.
[5] Yang He,Li Heng,Zhang Zhiyong,et al.Advances and Trends on Tube Bending Forming Technologies[J].Chinese Journal of Aeronautics,2012(25):1-12.
[6] 时立文.SPSS 19.0统计分析从入门到精通[M].北京:清华大学出版社,2012.
[7] 施彦,韩力群,廉小亲.神经网络设计方法与实例分析[M].北京:北京邮电大学出版社,2009.
Springback Prediction on Tube Bending Forming of Stainless Steel
WANGTianli1,LIANGZhenglong2,ZHANGShen2,WUJianjun2
(1.AVIC Xi’an Aircraft Industry(Group)Company Ltd.Xi’an 710089,China;2.School of Mechanical Engineering,Northwestern Polytechnical University,Xi’an 710072,China)
FEM software is used to build an effective simulation model on springback of stainless steel tube bending forming.The virtual orthogonal experiment method was used to research the factors those influence the springback,such as bending angle,diameter,tube thickness,assistant velocity and friction factor between bending die and outboard of tube.Then,linear regression analysis and artificial neural networks were employed to establish the mathematic relationship between springback angle and those factors.The results proved that springback angle is linear increase along with increase of bending angle obviously,compared with this,others have weekly influence;artificial neural networks was more precision.
stainless steel;springback;virtual orthogonal experiment;linear regression analysis;artificial neural networks
2014-09-22
TG386
A
1001-2257(2014)12-0027-04
王天立(1984-),男,内蒙古阿荣旗人,助理工程师,研究方向为数控弯曲成形技术;梁正龙(1990-),男,甘肃庄浪人,硕士研究生,研究方向为金属塑性成形技术;张深(1985-),男,辽宁兴城人,博士研究生,研究方向为精密加工与成形技术,计算机辅助成形与仿真;吴建军(1963-),男,陕西西安人,工学博士,博士研究生导师,教授,研究方向为材料成形机理,材料成形性评估以及成形过程分析模拟。

