高速入水子弹气动发射架设计建模

，

(1.福建福清核电有限公司,福建 福清 350318；2.西安陕鼓汽轮机有限公司，陕西 西安 710075)

高速入水子弹气动发射架设计建模

任艳军1，宋博义2

(1.福建福清核电有限公司,福建 福清 350318；2.西安陕鼓汽轮机有限公司，陕西 西安 710075)

研究了一种用于研究子弹在不同角度高速入水的气动发射架。主要从发射架结构构成、发射原理分析和计算机模拟等方面对发射架进行分析。建立了子弹发射过程的数学模型，选用Matlab软件对模型分析求解，得出了子弹速度的时域变化曲线。通过改变发射边界参数，对比得出各参数对子弹发射的影响。对子弹在不同角度下高速入水研究进行技术储备和参考，同时也为气动发射架的设计提供理论依据。

气动发射;发射架;系统仿真

0 引言

自从20世纪20年代末水上飞机的水面降落问题提出以来，结构物入水冲击的理论与试验研究得到了飞速发展，例如，水上飞机和宇宙飞船水面着陆、卫星海面回收、空投雷弹入水冲击、船舶在风浪中砰击和救生艇的海上抛落等[1-2]。回转体入水问题对导弹、鱼雷等的外形和弹道设计有着深远影响[3]。研究的发射架是一种用于高速入水实验的发射角度可调子弹发射架，主要用于研究子弹在0°～-30°范围内高速入水的空化现象，并对不同速度条件下子弹入水的空泡形态进行研究。

主要采用内弹道方程以及气体动力学方程对发射架系统的发射过程进行Matlab仿真，通过对储气仓状态，发射管压力以及子弹速度在时域的变化，将发射架工作分为阀工作过程和子弹出管过程进行计算，得出不同边界条件下子弹的出管速度。并通过与实验结果对比修正，为高速射弹方面的研究作参考。

1 发射架构型

1.1 总体结构

发射架设计条件是,子弹射出角度为0°～-30°；子弹出管速度为80m/s以上；采用压缩空气作为发射能源。

根据实验的边界条件以及工程经验，设计发射架三维结构如图1所示。

发射架主要由支架体、高压储气仓、进气接口、快速开关阀、枪管以及角度调节系统构成。发射分为准备阶段、发射阶段以及停止阶段。

图1 发射架本体三维结构

1.2 储气仓的设计

根据发射管长度以及直径的最大值，确定发射过程的最大耗气量。为确保发射过程压力下降在5%之内。由等熵膨胀过程得:

pvk=C

(1)

p为压力；v为比体积；k为绝热指数。

可知储气仓体积约为发射管体积的10倍以上。综合储气仓耐压性能和经济性，选择圆柱形储气仓。

1.3 支架设计

根据设计要求，支架角度为0°～-30°，出口高度为0.5m。为了保证发射管刚度以及直线度，当发射管长度不大于2m的情况下，采用单点支撑，支撑位置在气瓶中部；当发生管长度大于2m时采用出口支撑高度固定，中间支撑以及气瓶支撑采用丝杠以及螺纹套筒连接调节的支撑方式。

2 发射原理分析

根据气动发射原理，该发射架主要针对发射的热力学过程，运动学过程以及动力学过程进行了分析[4]。原理简图如图2所示。

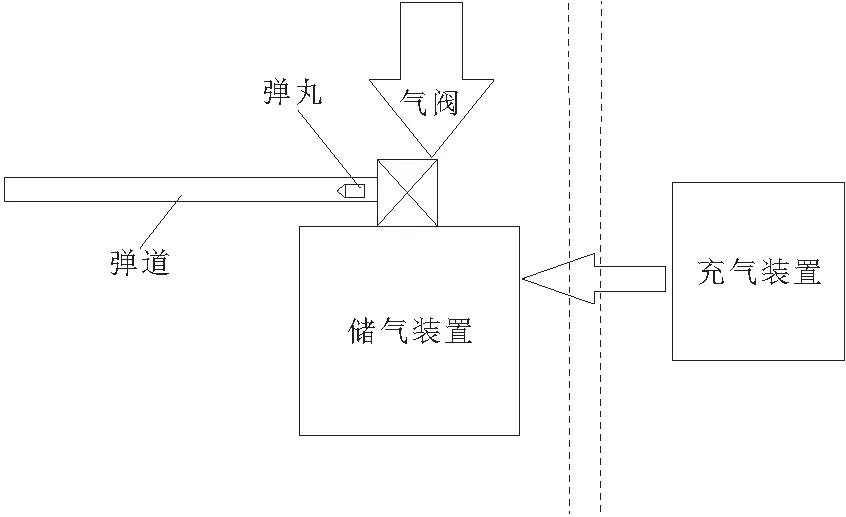
图2 发射原理

2.1 热力学过程

把热力系处于平衡状态时基本状态参数p,v,T之间的函数关系的状态方程为:

f(p,v,T)=0

(1)

在建立气动弹丸发射内弹道方程组时，提出如下假设。

a.假设工作介质为理想气体，气体流动和子弹运动都是一维沿轴向运动。

b.假定压缩气体在工作过程中某一瞬时的压力、密度和温度都是均匀分布的。

c.忽略气体容积余隙的影响。

d.对子弹前的空气阻力、弹道对弹丸的摩擦阻力进行修正，并忽略弹丸重力的影响。

e.高压储气仓内压缩气体经气阀开口流入管路内，并推动弹丸运动出弹道的过程在极短时间内完成，故认为是等熵膨胀过程，忽略气体与容器及出口管壁面的热交换。

基于以上假设，由理想气体的状态方程可知，对m气体，有:

pv=mRgT

(2)

m为气体的质量；Rg为气体常数。

而质量体积与密度间存在关系为:

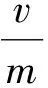
(3)

由此可得:

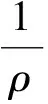
(4)

化简后密度为:

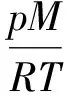
(5)

p为压力；R为摩尔气体常数，R=8314J/(mol·K)；T为开氏温度，这里取T=293K。

则该过程热力学方程可简化为:

(6)

k为绝热指数，这里取k=1.33。

2.2 沿程损失分析

压缩空气在横截面积不变的弹道内流动是层流状态时，其流量计沿程压力损失可由理论公式计算。

根据实际流体的伯努利方程

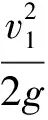
(7)

伯努利方程中hw一项，若仅考虑沿程损失，管径不变，则按伯努利方程得:

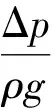
(8)

管中流动假设为层流，则有:

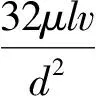
(9)

将式(9)代入式(8)中，可得:

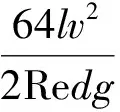
(10)

λ为沿程阻力损失系数;l为管道长度即弹道长;d为管内直径;v为平均流速。

式(10)为水平均匀圆管内充分发展流动的沿程损失计算公式，由此计算出沿程损失的压降为:

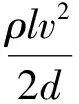
(11)

2.3 运动学过程及动力学过程

假定弹丸质量为m，弹道内直径为d，由式(5)可知，假定弹丸底部所受到的压力与当时气阀内压力一致，均为pg，气阀内压力与高压储气仓压力之间放气压力稍有损失，损失系数为0.95，在射击过程中，气阀阀口开启t时刻后，压力为p(t)，弹丸前进位移为x(t)，弹丸速度为v(t)，弹丸加速度为a(t)，出口压力为p(d)。弹丸的运动方程中，高压气体推力为:

Fg=ΔptA

(12)

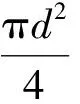
而沿程阻力为:

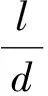
(13)

综上所述，可得:

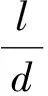
(14)

λ为沿程阻力损失系数；l为弹道长度；v为平均流速。

3 仿真结果及分析

3.1 仿真边界条件

弹道内气流参数的初始值：入口处气体初始压力范围为1～12MPa，出口处压力为大气压，发射管内径为10mm、子弹材料为45钢，质量为22.23g，设定其沿程阻力系数λ=0.025。绝热指数为:

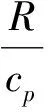
(15)

R=8.314 J/mol·K,μ为工质气体(空气)的分子量，μ=28.964 kg/kmol，由此可得，R=287 J/kg·K。由相关资料可得，在T=300K条件下，不同工况下子弹的速度变化如表1所示。由此可知，压力在1～10MPa时，绝热指数k取1.33～1.39。

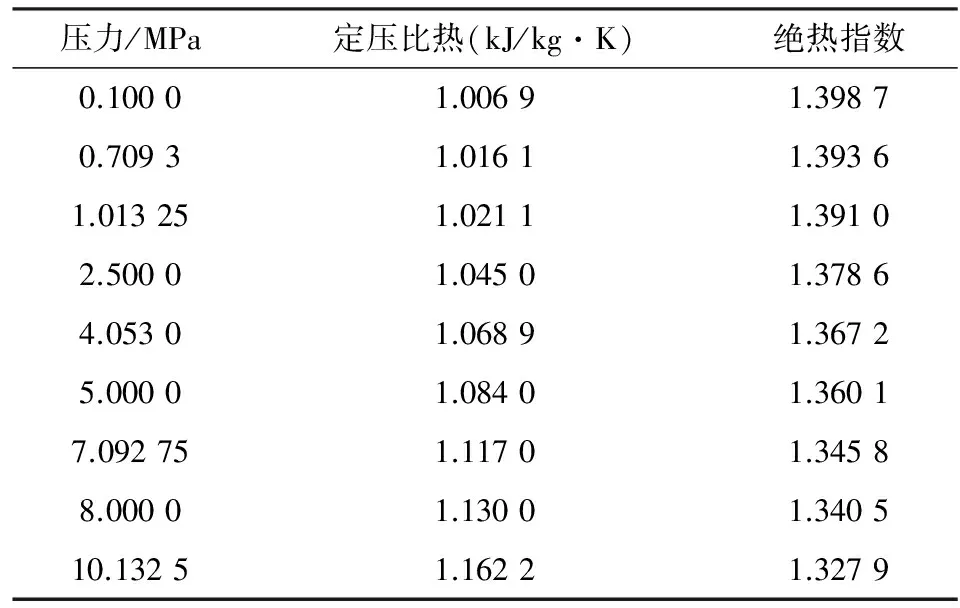
表1 不同工况下子弹速度变化

3.2 仿真结果

压缩气瓶的最高压力是13.5MPa，取最大发射初始压力为12MPa。通过Matlab仿真得到子弹的时间-速度曲线。改变储气仓压力对子弹速度的影响如图3所示。由此可得，压力越高，子弹获得的加速度越大。

改变发射管长度对子弹速度的影响曲线(气源初始压力12MPa条件下)如图4所示，由图中不难看出，在该边界条件下，子弹发射出管速度最高处为0.02s时，速度能达到190m/s以上，使用2.8m长发射管能使子弹充分加速。

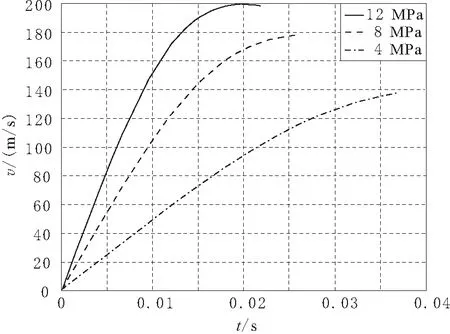
图3 压力影响曲线

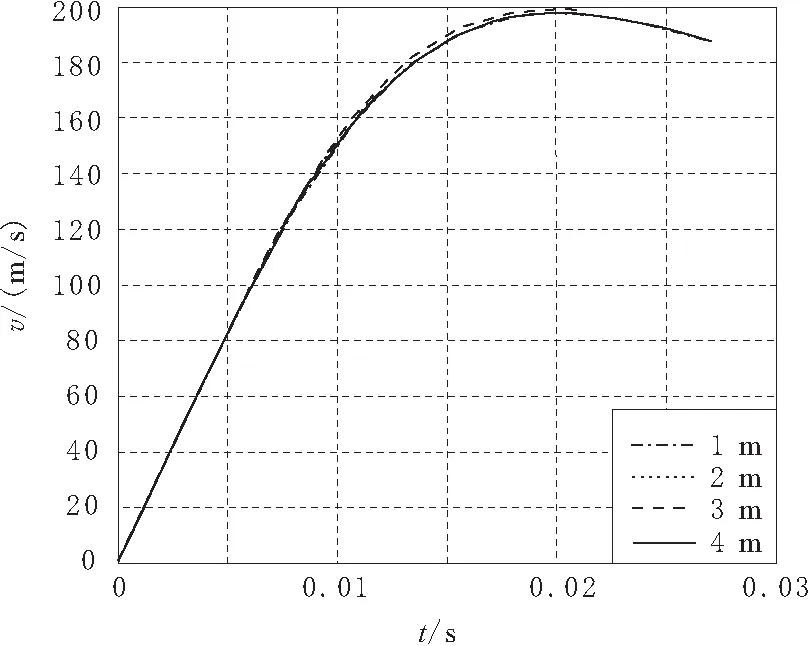
图4 发射管长度影响曲线

丰满系数对子弹发射速度的影响(气源初始压力12MPa条件下)如图5所示。丰满系数为子弹与发射管之间的间隙，丰满系数越高，间隙越小。由图可以看出，丰满系数约0.8时，子弹的加速时间最小，出管速度也最高。

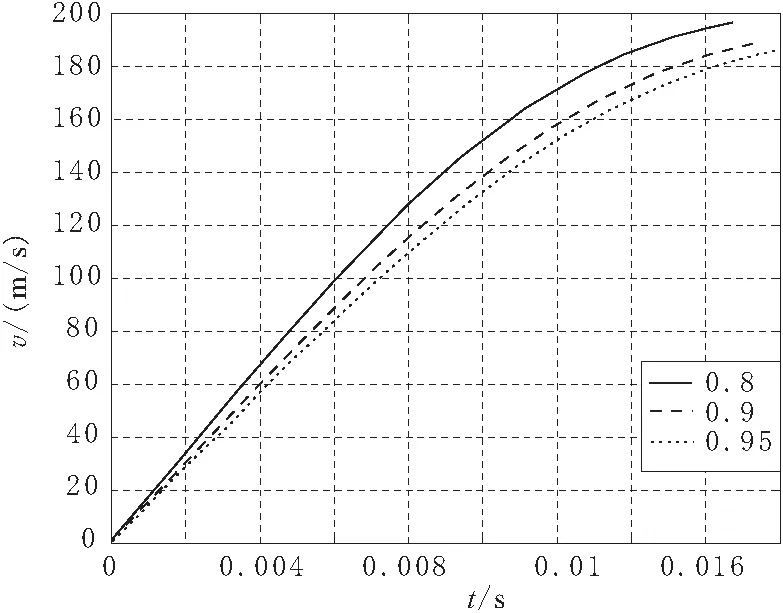
图5 丰满系数影响曲线

管内径对子弹出管速度的影响(气源初始压力12MPa条件下)如图6所示。由图可以看出，管径越小，子弹的加速性能越好，但是出管并不能充分加速。在10mm内径条件下，子弹的加速充分性和出管速度相对较好。

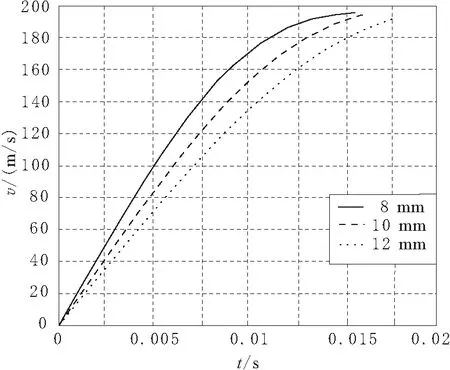
图6 发射管内径影响曲线

4 实验结果对比分析

发射及测速系统实验装置，主要用于研究子弹水平入水的入水速度和空化程度。气源压力为0～12MPa(可调节)；子弹质量为22.23g；发射管长度为2m；发射管直径为10mm；储气仓容积约为30L。

通过3次试验，对子弹入水的高速摄像结果分析和测量，得到子弹在不同压力下的入水速度如表2所示。

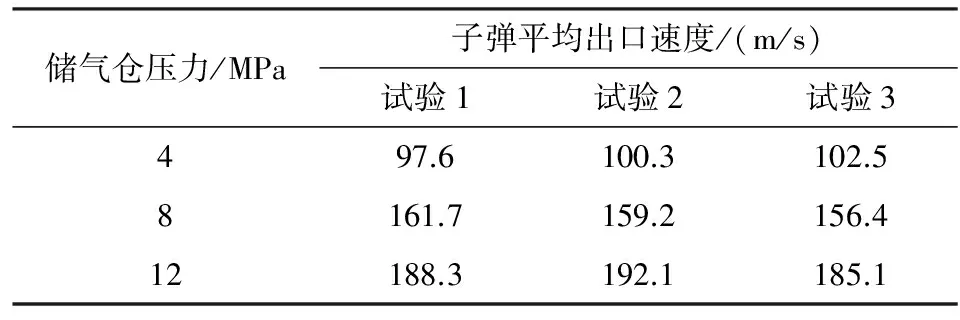
表2 试验中储气仓压力与子弹出口速度

由表2可知，在相同管长及储气仓容积的条件下，子弹出口速度随着压力的升高不断增加；试验结果仿真结果较为相似。但同时，由于开关截止阀为手动阀，人工操作时的全开时间一致性不高，导致测量结果有一定差异。

由于试验中选用的发射管长度为2m，子弹发射时间变短，在管内不能得到充分加速。而若需子弹得到充分加速，则在更换管长的同时要增加储气仓容积才能解决。

5 结束语

通过一种用于子弹高速入水可调角度的气动子弹发射架设计，利用软件对发射过程进行了仿真，并对不同边界条件对子弹出口速度的影响进行分析。通过与试验结果对比分析，证明了该仿真方法的实用性，也为设计和使用该种发射架提供参考依据。

[1] Wang Y,Shi X,Wang P.Dynamical response analysis of incautious water entry of UUV based on exact body shape approach[C]//7th World Congress on intelligent Control and Automation. Chongqing,China:IEEE,2008.4870-4875.

[2] Waugh J G.Water-entry pitch modeling[J].Journal of Hydronautics,1968,2(2):87-92.

[3] 邱海强,袁绪龙,王亚东,等.回转体高速垂直入水冲击载荷和空泡形态仿真[J].鱼雷技术,2013,3(21):161-164.

[4] 胡艳玲.气动枪械发射原理有关问题的研究[D].南京:南京理工大学,2008.

Bullet Pneumatic High-speed Water Entry Launcher Design and Modeling

RENYanjun1,SONGBoyi2

(1. Fuqing Nuclear Power Co.,Ltd.,Fuqing 350318,China;2.Xi’an Shanngu Steam Turbine Co.,Ltd.,Xi’an 71007,China)

This dissertation focuses on an angle adjustable bullet pneumatic emission launcher which is used to study the bullet enter water at high velocity.It is mainly analysis from the structure,principle and gets system simulation for the launcher.The bullet launch mathematic model is established,and solved with Matlab software.It is concluded the temporal change curve of the bullet velocity.Changing the boundary conditions and solving result.Compare the influence of conditions on the launch.The results were compared with the experimental correction to study technical reserves and reference in this area,and also provide theoretical basis for the design of the pneumatic launcher.

pneumatic emission;launcher;system simulation

2014-05-13

TJ27

A

1001-2257(2014)08-0030-04

任艳军(1986- )，男，陕西榆林人，助理工程师，研究方向为核电动力系统运营;宋博义(1985-),男，陕西西安人，助理工程师，研究方向为热能工程及能量转换机械。