Hom-dimodules and FRT theorem of Hom type
Chen Xiuli Li Fang Chen Jianlong
(1Department of Mathematics, Southeast University, Nanjing 211189, China)(2Department of Mathematics, Zhejiang University, Hangzhou 310028, China)
Hom-dimodules and FRT theorem of Hom type
Chen Xiuli1Li Fang2Chen Jianlong1
(1Department of Mathematics, Southeast University, Nanjing 211189, China)(2Department of Mathematics, Zhejiang University, Hangzhou 310028, China)
In order to study the deformation of algebras, the notions of Hom-algebras are introduced. The Hom-algebra is a generalization of the classical associative algebra. First, the Hom-type generalization of dimodules, which is called the Hom-dimodule, is introduced, and its properties are discussed Moreover, the category of Hom-dimodules in connection with the Hom D-equationR12R23=R23R12forR∈Endk(M⊗M)and a Hom-moduleMis investigated. Some solutions of the Hom D-equation from Hom-dimodules over Hom-bialgebras are given, and the FRT-type theorem is constructed in the category of Hom-dimodules. The results generalize and improve the FRT-type theorem in the category of dimodules.
Hom-bialgebra; Hom-dimodule; Hom D-equation
Throughout this paper, all the modules are left modules without specification and all the spaces arek-spaces for a fixed fieldk.
A (long) dimodule over a bialgebraHis a vector spaceMwith a leftH-actionρMand a rightH-coactionρMso that the following compatibility condition holds: (hm)(0)⊗(hm)(1)=∑hm(0)⊗m(1)for allh∈Handm∈M. We denote this category withHLH, which is also a special case of the Doi-Hopf module category. This categoryHLHwas first defined by Long[1]for a commutative and cocommutativeHand was studied in connection with the construction of the Brauer group of anH-dimodule algebra. It is interesting to note that for a commutative and cocommutativeH,HYDH(the category of Yetter-Drinfel’d modules) is preciselyHLH[2]. Naturally, for an arbitraryH,HYDHandHLHare fundamentally different.HYDHplays a determinant role in describing the solutions of the quantum Yang-Baxter equation. It is natural to ask which equation will play a key role inHLH. In Ref.[3], considering thatHYDHis deeply involved in solving the quantum Yang-Baxter equation, the author studiedHLHin connection with the D-equation which is described presently. Given a vector spaceM, andR∈Endk(M⊗M),Ris said to be a solution of the D-equation ifR12R23=R23R12in Endk(M⊗M⊗M) whereR12=R⊗id, andR23=id⊗R.
The concept of a Hom-algebra was introduced by Larsson et al[4-5]. It is a special class in the deformation of algebras. Recently, the Hom-algebra has been studied by several authors. The further development of the Hom-algebra theory led Makhlouf et al.[6-8] consequently to Hom-associative algebra, Hom-coassociative coalgebra and Hom-bialgebra, and described many of the extending properties of classical associative algebras, coalgebras, bialgebras and Hopf algebra structures. In fact, the notion of Hom-associative algebras generalize associative algebras to a situation, where associativity law is twisted by a linear map. From Ref.[5], it is clear that the commutator bracket multiplication is defined using the multiplication in Hom-associative algebra and it leads naturally to Hom-Lie algebras. Following the patterns of Hom-Lie and Hom-associative algebras, one can define Hom-bialgebras as nonassociative and non-coassociative[9]. It is a generalization of the bialgebra in which the non(co)associativity is controlled by the twisted map. In this paper, we only investigate the case of Hom-associative algebras. Hom-versions of the Yang-Baxter equation was studied in Refs.[9-12]. Many classes of the solutions for the Hom-Yang-Baxter equation are constructed. Moreover, Hom-type generalizations of FRT quantum groups, including quantum matrices and related quantum groups, are obtained in Ref.[13]. The above motivates us to study the generalization of the D-equation.
In this paper, we mainly study Hom-versions of (Long) dimodules and D-equations of the Hom type, and investigate the category of Hom-dimodules in connection with the Hom D-equation.
1 Preliminaries
In this section, we recall the definition of a Hom-bialgebra and (comodules)modules over an Hom-algebra(coalgebra).
A Hom-module[14]is a pair (V,α) in whichVis a vector space andα:V→Vis a linear map. A morphism (V,α)→(V′,α′) of Hom-modules is a linear mapf:V→V′ such thatα′∘f=f∘α. The tensor product of the Hom-modules (V,αv)and (W,αw) consists of the vector spaceV⊗Wand the linear self-mapαV⊗αW.
Definition 1 A Hom-associative algebra[5]is a triple(A,μ,α)in which (A,α)is a Hom-module andμ:A⊗A→Ais a bilinear map such that 1)α∘μ=μ∘ (α⊗α)(multiplicativity); and 2)μ∘ (α⊗μ)=μ∘ (μ⊗α)(Hom-associativity). In the following, we also writeμ(a⊗b)asab.
The Hom-associative algebra is said to be unital[7]if a homomorphism exists,η:k→Asatisfyingμ∘ (η⊗id)=idandμ∘ (id⊗η)=id.
A Hom-coassociative coalgebra[6-7]is a triple(C,Δ,α)in which (C,α) is a Hom-module andΔ:C→C⊗Cis a linear map such that 1)α⊗2∘Δ=Δ∘α(comultiplicativity); and 2) (α⊗Δ)∘Δ=(Δ⊗α)∘Δ(Hom-coassociativity).
A Hom-coassociative coalgebra is said to be counital[7]if there is a mapε:C→ksatisfying (ε⊗id)∘Δ=idand (id⊗ε)∘Δ=id.
Example 1(classical structures) 1) If (A,μ) is an associative algebra andα:A→Ais an algebra morphism, thenAα=(A,μα,α) is a Hom-associative algebra with the twisted multiplicationμα=α∘μ. Indeed, the Hom-associativity axiomμα∘ (α⊗μα)=μα∘ (μα⊗α) is equal toα2when applied to the associativity axiom ofμ. Likewise, both sides of the multiplicativity axiomα∘μα=μα⊗(α⊗α)are equal toα2∘μ.
2) Dually, if (C,Δ) is a coassociative coalgebra andα:C→Cis a coalgebra morphism, thenCα=(C,Δα,α) is a Hom-coassociative coalgebra with the twisted comultiplicationΔα=Δ∘α.
3) A bialgebra is an exact Hom-bialgebra withα=id. More generally, combining the previous two cases, if (A,μ,Δ) is a bialgebra andα:A→Ais a bialgebra morphism, thenAα=(A,μα,Δα,α) is a Hom-bialgebra.
Definition 2 1) Let (A,μA,αA) be a Hom-associative algebra, and (M,αM) be a Hom-module. A leftA-module structure onM[12]consists of a morphismρ:A⊗M→Mof Hom-modules such thatρ∘ (αA⊗ρ)=ρ∘ (μA⊗αM) andαM∘ρM=ρM∘ (αH⊗αM) (*). We also writeρ(a⊗m) asamfora∈Aandm∈M. In this notation, (*) can be written asαA(a)(bm)=(ab)αM(M) andαM(ax)=αA(a)αM(x).
2) Dually, let (C,Δ,αC) be a Hom-coassociative coalgebra,AleftC-comodule structure onM[14]consists of a Hom-module (M,αM) together with a linear mapρM:M→C⊗Msuch that (Δ⊗αM)∘ρM=(αC⊗ρM)∘ρMand (αC⊗αM)∘ρM=ρM∘αM. Similarly, we can define a rightC-comodule.
IfMandNareA-modules, then a morphism ofA-modulesf:M→Nis a morphism of the Hom-modules such thatf∘ρM=ρN∘ (idA⊗f). Similarly, morphisms ofC-comodule are defined in a clear way.
2 Hom-Dimodules
Definition 3 Let (H,μH,ΔH,αH) be a Hom-bialgebra, and (M,αM)be a Hom-module. A Hom-dimodule is a triple (M,ρM,ρM) such that 1) (M,ρM) is a leftH-module; 2) (M,ρM) is a rightH-comodule; 3)ρM∘ρM=(ρM⊗αM)∘ (αH⊗ρM).
We may also write 3) as (hm)(0)⊗(hm)(1)=∑αH(h)m(0)⊗αH(m(1)).
The category of Hom-dimodules over a Hom-bialgebraHwithH-module morphisms andH-comodule morphisms are denoted byHHLH.
IfHis a bialgebra, i.e.,αH=idHandαM=idM, then the above definition of the Hom-dimodule coincides with the usual definition of the dimodule. The following result proves that dimodules deform into Hom-dimodules by endomorphisms.
Proposition 1 Let (H,μH,ΔH) be a bialgebra, and (M,ρM,ρM) be anH-dimodule. Assume thatαH:H→His a bialgebra morphism, andαM:M→Mis ak-linear map such that
αM∘ρM=ρM∘ (αH⊗αM)
(1)
ρM∘αM=(αH⊗αM)∘ρM
(2)

1) (H,μα,Δα,αH) is a Hom-bialgebra, whereμα=αH∘μHandΔα=ΔH∘αH;
2) (M,ρα,M,ρα,M) is a Hom-dimodule over a Hom-bialgebraH, whereHis a Hom-bialgebra as 1).
Proof 1) It follows from 1) of Example 1.
2) First, by Definition 1 and Eq.(2), it is easy to prove thatρα,Mgives (M,αM) the structure of a leftH-module, i.e.,ρα,M∘ (αH⊗ρα,M)=ρα,M∘ (μH⊗αM).
Similarly, by Definition 2, we can prove thatρα,Mgives (M,αM) the structure of a rightH-comodule if and only if (ρα,M⊗αH)∘ρα,M=(αM⊗ΔH)∘ρα,M.
Finally, it is only needed to check thatρα,M∘ρα,M=(ρα,M⊗αH)∘ (αH⊗ρα,M). In fact, we have
ρα,M∘ρα,M=(ρM∘αM)∘ (αM∘ρM)=
(αM⊗αH)∘ρM∘ρM∘ (αH⊗αM)=
(αM⊗αH)∘ (ρM⊗idH)∘ (idH⊗ρM)∘ (αH⊗αM)=
(ρα,M⊗αH)∘ (αH⊗ρα,M)
where the second equality holds by Eqs.(1) and (2). BecauseMis aH-dimodule, the third equality holds.
Proposition 2 Let (H,μH,ΔH,αH)be a Hom-bialgebra, (M,αM) and (N,αN) be Hom-dimodules. ThenM⊗Nis a Hom-dimodule with the action and coaction, for allm∈M,n∈N,h∈H,
ρM⊗N(h⊗m⊗n)=αH(h(1))·m⊗αH(h(2))·n
ρM⊗N(m⊗n)=m(0)⊗n(0)⊗αH(m(1)n(1))
Proof We check thatρM⊗NandρM⊗Nis well defined. For anyh,l∈H,m∈Mandn∈N,
ρM⊗N∘ (αH⊗ρM⊗N)(h⊗l⊗m⊗n)=
ρM⊗N(αH(h)⊗αH(l(1))·m⊗αH(l(2))·n)=
αH((αH(h)(1))αH(l(1))·m)⊗αH(αH(h))(2))(αH(l(2))·n)=

(αH(h(1))αH(l(1))·αM(m)⊗(αH(h(2))αH(l(2)))αN(n)=
aH((hl)(1))αM(m)⊗αH((hl)(2))αN(n)=
ρM⊗N(hl⊗αM(m)⊗αN(n))=
pM⊗N∘ (μH⊗αM⊗N)(h⊗l⊗m⊗n)

ρM⊗N∘ρM⊗N(h⊗m⊗n)=ρM⊗N(αH(h(1))·m⊗αH(h(2))·n)=
(αH(h(1))·m)(0)⊗(αH(h(2))·n)(0))⊗αH((αH(h(1))·m)(1)
αH(αH(m(1))αH(n(1)))=(ρM⊗N⊗αH)(αH(h)⊗m(0)⊗
n(0)⊗αH(m(1))αH(n(1)))=(ρM⊗N⊗αH)∘
(αH⊗ρM⊗N)(h⊗m⊗n)
3 Solutions of Hom D-Equation
First we introduce the definition of the Hom D-equation. Moreover, we construct many solutions to the Hom D-equation by Hom-dimodules over the Hom-bialgebra.
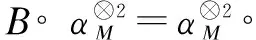
The D-equation[3]is a special case of the Hom D-equation whenα=id.
Proposition 3 LetBbe a solution of the Hom D-equation for the Hom-module (M,αM).
1) Ifλ∈k, thenλBis also a solution of the Hom D-equation for (M,αM).

Proof 1) First,λB∘ (αM⊗αM)=λ(B∘ (αM⊗αM))=λ((αM⊗αM)∘B)=(αM⊗αM)∘λB, andλB⊗α=λ(B⊗α),α⊗λB=λ(α⊗B), so we have (λB)12(λB)23=(λB)23(λB)12.
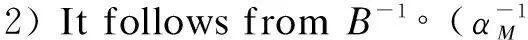
Next, we will show that a Hom-bialgebra gives rise to many solutions of the Hom D-equation by its Hom-dimodules. The following shows thatHHLHplays a role in solving the Hom D-equation.
Proposition 4 Let (H,μH,ΔH,αH) be a Hom-bialgebra, and (M,αM) be a Hom-module. Assume that (M,ρα,M,ρα,M) is Hom-dimodule andαMis anH-module morphism. Then the map
B′:M⊗M→M⊗M,m⊗n|→αH(n(1))·m⊗αM(n(0))
(3)
is a solution of the Hom D-equation.
Proof First, it is easy to check thatB′∘ (αM⊗αM)(m⊗n)=(αM⊗αM)∘B′(m⊗n).
Forl,m,n∈M, we have
B′12B′23(l⊗m⊗n)=(B′⊗αM)(αM⊗B′)(l⊗m⊗n)=
(B′⊗αM)(αM(l)⊗αH(n(1))·m⊗αM(n(0)))=
αH((αH(n(1))·m)(1))·αM(l)⊗αM((αH(n(1))·m)(0))⊗
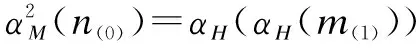

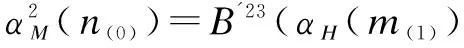
B′23B′12(l⊗m⊗n)
The fourth equality holds because (M,αM) is a Hom-dimodule. SinceαMisH-module morphism, the fifth equality is true. By 2) of Definition 2, we haveαM(m(0))⊗αH(m(1))=(αM(m))(0)⊗(αM(m))(1), so the sixth equality holds by (3). Therefore,B′12B′23=B′23B′12, i.e.,B′ is a solution of the Hom D-equation.
Corollary 1 Let (H,μH,ΔH) be a bialgebra, andαH:H→Hbe a bialgebra morphism. Assume that (M,ρM,ρM) is a dimodule andαM:M→Mak-linear map such thatαM∘ρM=ρM∘ (αH⊗αM), andρM∘αM=(αM⊗αH)∘ρM. IfαMisH-module morphism. Then the map (3) is a solution of the Hom D-equation.
In Corollary 1, ifαH=id:H→H, then the conditionsαM∘ρM=ρM∘ (id⊗αM) andρM∘αM=(αM⊗idH)∘ρMmean thatαMisH-module morphism andH-comodule a morphism. So we have the following corollary.
Corollary 2 Let (H,μH,ΔH) be a bialgebra. Assume that (M,ρM,ρM) is a dimodule andαM:M→MisH-module morphism andH-comodule morphism. Then the map (3) is a solution of the Hom D-equation.
4 FRT Theorem of Hom Type
In Ref.[7], the authors give a FRT type theorem: ifMis finite dimensional, then any solutionRof the D-equation has the formR=R(M,ρM,ρM), where (M,ρM,ρM) is aD(R)-dimodule over a bialgebraD(R) andR(M,ρM,ρM)is the special mapR(M,ρM,ρM)(m⊗n):=∑n(1)m⊗n(0).
Next, we recall the details of the FRT type construction from Theorem 3.6 in Ref.[3].


(4)
for allu,v=1,2,…,n.
LetT(C)be an algebra generated by (Cij). Define the bialgebra
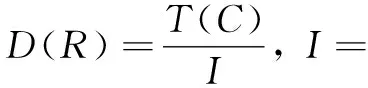
(5)

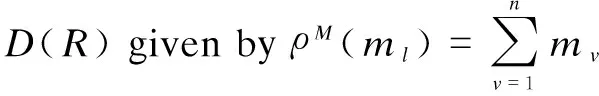

Lemma 1 LetD(R) be the bialgebra withR:M⊗M→M⊗Ma solution of theD-equation, and assume that (M,ρM,ρM) has the structure of the object inD(R)LD(R), whereR=R(M,ρM,ρM). Letλi∈kbe invertible scalars such that
(6)
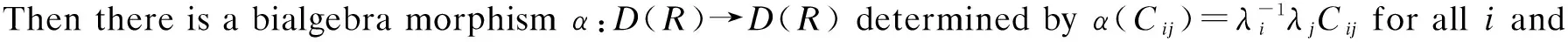

In fact,
The third equality is right by (6), the fourth equality follows from (5), and the fifth equality also follows from (6).
Lemma 2 The linear mapαM:M→Mcan be defined asαM(mi)=λimifor alli. Then we have
αM∘ρM=ρM∘ (α⊗αM)
(αM⊗α)∘ρM=ρM∘αM
(αM⊗αM)∘R=R∘ (αM⊗αM)
whereρM:D(R)⊗M→Mis the leftD(R)-module structure map andρM:M→M⊗D(R) is the rightD(R)-comdule structure map.
Proof First, sinceΔis an algebra morphism, we have
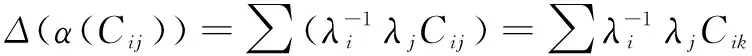
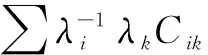
This shows thatαis a bialgebra morphism. Next,
αM∘ρM(Cju⊗mv)=αM(Cju·mv)=
and
ρM∘ (α⊗αM)(Cju⊗mv)=α(Cju)·αM(mv)=
soαM∘ρM=ρM∘ (α⊗αM).
Since
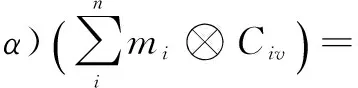

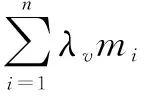
(αM⊗α)∘ρM=ρM∘αMholds.
Finally,
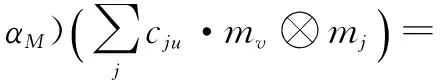

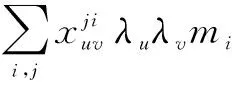
So (αM⊗αM)∘R=R∘ (αM⊗αM) is true.

Proof It follows with Proposition 1, Lemma 1 and Lemma 2.


Therefore, by Theorem 1, we obtain the Hom-bialgebraD(R)α=(D(R),μα=α∘μ,Δα=Δ∘α) such that (M,ρα,M=αM∘ρM,ρα,M=αM∘ρM) is a HomD(R)-dimodule.
Remark 2 Example 2 also gives an example of Hom-dimodules.
[1]Long F W. The Brauer group of dimodule algebras [J].JournalofAlgebra, 1974, 31(1/2/3): 559-601.
[2]Caenepeel C, Militaru G, Zhu S L. Crossed modules and Doi-Hopf modules [J].IsraelJournalofMathematics, 1997, 100(4): 221-247.
[3]Militaru G. The long dimodules category and nonlinear equations [J].AlgebrasandRepresentationTheory, 1999, 2(2): 177-200.
[4]Larsson D, Silvestrov S D. Quasi-Hom-Lie algebras, central extensions and 2-cocycle-like identities [J].JournalofAlgebra, 2005, 288(2): 321-344.
[5]Makhlouf A, Silvestrov S. Hom-algebra structures [J].JournalofGeneralizedLieTheoryandApplications, 2008, 2(2): 51-64.
[6]Makhlouf A, Silvestrov S. Hom-Lie admissible Hom-coalgebras and Hom-Hopf algebras [M]//GeneralizedLietheoryinmathematics,physicsandbeyond. Berlin: Springer, 2009:189-206.
[7]Makhlouf A, Silvestrov S. Hom-algebras and Hom-coalgebras [J].JournalofAlgebraandItsApplications, 2010, 9(4): 1-37.
[8]Yau D. Hom-bialgebras and comodule Hom-algebras [J].InternationalElectronicJournalofAlgebra, 2010, 8: 45-64.
[9]Yau D. The classical Hom-Yang-Baxter equation and Hom-Lie bialgebras [EB/OL]. (2009-05-12)[2013-02-27]. http://arxiv.org/abs/0905.1890.
[10]Yau D. The Hom-Yang-Baxter equation, Hom-Lie algebras, and quasi-triangular bialgebras [J].JournalofPhysicsA, 2009, 42(16):165202-1-165202-12.
[11]Yau D. The Hom-Yang-Baxter equation and Hom-Lie algebras [J].JournalofMathematicalPhysics, 2011, 52(5): 053502-1-053502-19.
[12]Yau D. Hom-quantum groups Ⅰ: quasi-triangular Hom-bialgebras [J].JournalofPhysicsA, 2012, 45(6): 065203-1-065203-23.
[13]Yau D. Hom-quantum groups Ⅱ: cobraided Hom-bialgebras and Hom-quantum geometry [EB/OL]. (2009-07-10)[2013-02-27]. http://arxiv.org/abs/0907.1880.
[14]Yau D. Enveloping algebras of Hom-Lie algebras [J].JournalofGeneralizedLieTheoryandApplications, 2008, 2(2): 95-108.
Hom-dimodules与Hom型的FRT定理
陈秀丽1李 方2陈建龙1
(1东南大学数学系, 南京 211189)(2浙江大学数学系, 杭州 310028)
为了研究代数形变理论,引入了Hom-代数的概念.事实上Hom-代数是经典结合代数的推广.首先介绍了dimodule的Hom型推广,即Hom-dimodule,并对其相关性质进行讨论.进一步研究了Hom-dimodule范畴与Hom D-方程R12R23=R23R12的关系,其中R∈Endk(M⊗M)且M为Hom模.针对Hom双代数上的Hom-dimodule给出了Hom D-方程的一些解,并在Hom-dimodules范畴中构造FRT-型定理.这些结果推广并改进了dimodule范畴中的FRT-型定理.
Hom双代数; Hom-dimodule; Hom D-方程
O153
s:The National Natural Science Foundation of China (No.11371089), the Specialized Research Fund for the Doctoral Program of Higher Education (No.20120092110020), the Postdoctoral Innovation Funds of Southeast University (No.3207013601).
:Chen Xiuli, Li Fang, Chen Jianlong.Hom-dimodules and FRT theorem of Hom type[J].Journal of Southeast University (English Edition),2014,30(3):391-395.
10.3969/j.issn.1003-7985.2014.03.025
10.3969/j.issn.1003-7985.2014.03.025
Received 2013-03-28.
Biographies:Chen Xiuli (1980—), female, doctor; Chen Jianlong (corresponding author), male, doctor, professor, jlchen@seu.edu.cn.
 Journal of Southeast University(English Edition)2014年3期
Journal of Southeast University(English Edition)2014年3期
- Journal of Southeast University(English Edition)的其它文章
- P-FFT and FG-FFT with real coefficients algorithm for the EFIE
- Compressed sensing estimation of sparse underwateracoustic channels with a large time delay spread
- Improved metrics for evaluating fault detection efficiency of test suite
- Early-stage Internet traffic identification based on packet payload size
- An adaptive generation method for free curve trajectory based on NURBS
- Stability analysis of time-varying systems via parameter-dependent homogeneous Lyapunov functions
