利用展开法求非线性方程的精确解*

董长紫

(陇东学院数学与统计学院，甘肃 庆阳 745000)

董长紫

(陇东学院数学与统计学院，甘肃 庆阳 745000)

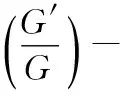
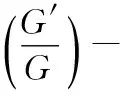
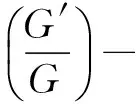
1 方法简述

对于偏微分方程

P(u,ux,ut,uxx,uxt,utt,…)=0，

(1)

假设有如下形式的解：

u(x,t)=φ(ξ),ξ=k(x-λt+c0)，

(2)

其中k,λ均是要被确定的参数，c0为任意的常数.(2)式代入(1)式，则只需处理常微分方程

(3)

第1步 假设φ(ξ)有以下的形式:

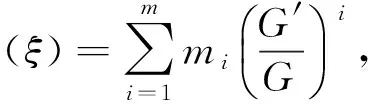
(4)

G=G(ξ)满足二次微分方程

G″(ξ)+h0G′(ξ)+h1G(ξ)=0，

(5)

其中m0，mi,…，h0,h1均为待定常数，指数m的值则可以通过平衡方程(3)中的最高次非线性项和最高次的偏微分项的次数而确定.

第4步 解在第3步中得到的代数系统，可得所设参数m0,…，mi,h0,h1的值，根据方程(4)，(5)的解得到φ(ξ)的结果，即方程(1)的行波解.

2 主要结果

2.1Burgers￣Fisher方程的精确解

在研究流体物理、等离子体物理、化学物理中的一些非线性现象时，经常会利用一般形式的Burgers￣Fisher方程

ut+aunux+buxx+cu(1-un)=0，

(6)

其中a,b,c均为常数.

首先，对给定的Burgers￣Fisher方程(6)做变换

u(x,t)=φ(ξ),ξ=k(x-λt+c0).

(7)

将(7)式代入(6)式可得

-kλφ′(ξ)+akφ″(ξ)φ′(ξ)+bk2φ″(ξ)+cφ(ξ)(1-φn(ξ))=0.

(8)

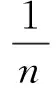
-kλv′v+ankv2v′+nbk2v″v+bk2(1-n)(v′)2+cn2v2-cn2v3=0.

(9)

平衡(9)式中v2v′与vv″的次数可得M=1.

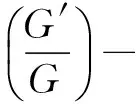
(10)

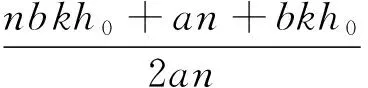
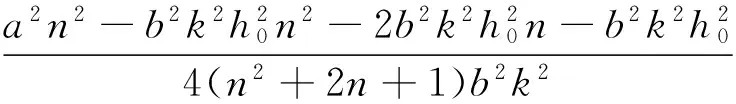
并将其结果代入(10)式，则根据(5)式的解可得方程(6)以下形式的行波解：

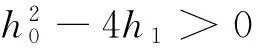
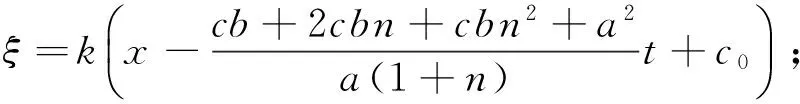
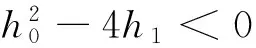
(11)

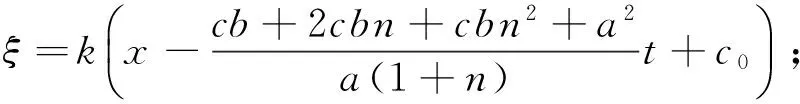
文献[14]中利用Riccati-方程的特殊结果得到(6)式的一些精确解，相比文献[14]中的结果，文中出现的解更具一般性，且含正余弦形式的行波解(11)是新的结果.

2.2Konopelchenko￣Durovsky方程的精确解

首先，对给定的Konopelchenko￣Durovsky方程

(12)

作变换

(13)

其中：ξ=k(x+ly-λt+c0)；k,λ,l为所要计算的常数；c0为任意常数.

将(13)式代入(12)式可得

(14)

将(14)式中的第2式代入第1式，且关于ξ积分1次，取积分常数为0可得

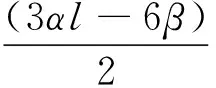
(15)

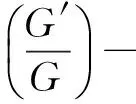
(16)

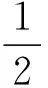
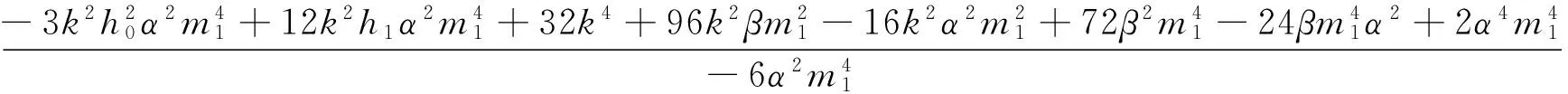
并将其结果代入(16)式，则根据(5)式的解可得原方程组(12)式以下形式的精确解：

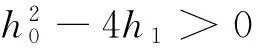
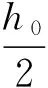
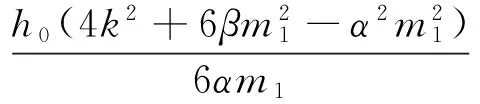
其中

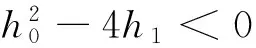
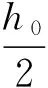
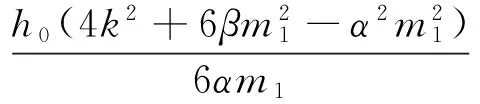
(17)

其中

3 结语

[1] DEBTNATH L.Nonlinear Partial Differential Equations for Scientist and Engineers[M].Boston,MA:Birkhauser,1997.

[2] WAZWAZ A M.Partial Differential Equations:Methods and Applications[M].Rotterdam：Balkema Publishers,2002.

[3] WANG Mingliang.The Solitary Wave Solutions for Variant Boussinesq Equations[J].Phys. Lett. A,1995,199:167-172.

[4] WANG Mingliang.Exact Solutions for a Compound KdV￣Burgers Equation[J].Phys. Lett. A,1996,213:279-287.

[5] 范恩贵,张鸿庆.非线性波动方程的孤波解[J].物理学报,1997,46:1 254-1 257.

[6] FAN Engui.Extended Tanh￣Function Method and Its Application tonon Linear Equation[J].Phys. Lett. A,2000,277:212-218.

[7] FAN Engui.Soliton Solutions for a Generalized Hirota Satsuma Coupled KdV Equation and a Coupled MKdV Equation[J].Phys. Lett. A,2001,282:18-22.

[8] 徐桂琼,李志斌.构造非线性发展方程孤波解的混合指数方法[J].物理学报,2002,51:946-950.

[9] 徐桂琼,李志斌.扩展的混合指数方法及其应用[J].物理学报,2002,51:1 424-1 427.

[10] 郭美玉,高 洁.耦合KdV 方程组的对称及精确解[J].聊城大学学报:自然科学版,2008,21:28-31.

[11] ZHAO Dun,LUO Honggang,WANG Shunjin.A Direct Truncation Method for Finding Abundant Exact Solutions and Application to the One￣Dimensional Higher￣Order Schrodinger Equation[J].Chaos,Solitons and Fractals,2005(24):533-547.

[14] SONG Li’na,ZHANG Hongqing.New Exact Solutions for the Konopelchenko￣Dubrovsky Equation Using an Extended Riccati Equation Rational Expansion Method and Symbolic Computation[J].Applied Mathematics and Computation,2007,187:1 373-1 388.

[15] LUWAI WAZZAN.A Modified Tanh￣Coth Method for Solving the General Burgers￣Fisher and the Kuramoto￣Sivashinsky Equations[J].Commun Nonlinear Sci. Numer. Simulat.,2009,14:2 642-2 652.

(责任编辑 向阳洁)

DONG Changzi

(Department of Mathematics and Statistics,Longdong University,Qingyang 745000,Gansu China )

1007-2985(2014)03-0015-05

2013-11-26

陇东学院青年科技创新项目(XYZK1109)

董长紫(1977-),男，甘肃庆阳人，陇东学院数学与统计学院讲师，硕士，主要从事数学物理方程研究.

O175.2

A

10.3969/j.issn.1007-2985.2014.03.004