Shape retrieval using multi-level included anglefunctions-based Fourier descriptor
Xu Guoqing Mu Zhichun Xu Ye
(School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China)
Shape retrieval using multi-level included anglefunctions-based Fourier descriptor
Xu Guoqing Mu Zhichun Xu Ye
(School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China)
An effective shape signature, namely multi-level included angle functions (MIAFs), is proposed to describe the hierarchy information ranging from global information to local variations of shape. Invariance to rotation, translation and scaling are the intrinsic properties of the MIAFs. For each contour point, the multi-level included angles are obtained based on the paired line segments derived from unequal-arc-length partitions of contour. And a Fourier descriptor derived from multi-level included angle functions (MIAFD) is presented for efficient shape retrieval. The proposed descriptor is evaluated with the standard performance evaluation method on three shape image databases, the MPEG-7 database, the Kimia-99 database and the Swedish leaf database. The experimental results of shape retrieval indicate that the MIAFD outperforms the existing Fourier descriptors, and has low computational complexity. And the comparison of the MIAFD with other shape description methods also shows that the proposed descriptor has the highest precision at the same recall value, which verifies its effectiveness.
shape description; image retrieval; multi-level included angle function; Fourier descriptor
As one of the primary visual contents of images used in CBIR, shape is clearly an important cue for representing and indexing images. However, shape description is a difficult task[1], as shape instances from the same category are often very different due to various transformations, such as translation, rotation, scaling, noise and occlusion, etc.[2]. In the last decade, significant progress has been made in the development of shape description and matching, and many shape description methods have been proposed[3]. Among many existing shape descriptors, the Fourier descriptor (FD) is a classical method and it is very popular due to its low computational complexity, clarity and coarse-to-fine description[3-4]. FD methods use a 1-D feature function called shape signature, to represent a 2-D shape contour. Different feature functions have different capabilities of describing contour, and, hence, FDs derived from different feature functions have significantly different retrieval performance[5]. In recent years, several new signatures have been developed, such as the perimeter area function (PAF)[6], the farthest point distance (FPD)[5], and the arc-height radius complex function (AHRC)[7].
The FPD is expected to increase the capability of the FD to capture local corner information. For a given point on the shape contour, the FPD value is calculated by adding the distance between the given point and the centroid to that between the centroid and the point farthest from the given point. Therefore, the FPD is still affected by the centroid in essence, and it cannot describe the local detail information very well.
The PAF places all the vertices of the triangle on the shape contour and can well capture local contour information. And the Fourier features derived from the PAF are combined with the ones derived from the centroid distance (CD) for shape retrieval. The experimental results show that this method outperforms commonly used FDs and the wavelet Fourier descriptor[6]. Much similar to the PAF, the AHRC also uses contour points to produce the signed arc-height features[7]. The AHRC is a complex-valued signature formed by combining the centroid distance and the signed arc-height, and it is analogous to the angular radius function[8]. The FDs derived from the AHRC function can be regarded as the arc-height radius Fourier descriptor (AHRFD).
However, the combination of local and global features, such as PAF+CD, fails to reflect the hierarchy of the diversity between local and global information very well. Another way to capture both local and global information can be achieved by using the multi-scale methods[6,9-10]. In Ref.[9], the beam angle statistics (BAS) descriptor was proposed. Beams are defined as vectors connecting a contour point with the remaining points on the contour, and the slopes of the beams are used to calculate the angle between each pair of beams. However, the usage of the statistics of the beam angles at all scales and the optimal correspondence algorithm increases the computational complexity. In Ref.[10], the angle scale descriptor (ASD) was introduced to eliminate the noise influence in the angle calculation. In the ASD, the angle at a point is formed by two successive vectors. However, the usage of consecutive angle’s scaling makes the information in feature vectors redundant. And the amount of computation increases accordingly. It is clear that both of the two descriptors do not rationally exploit the information provided by the angles. The proposed MIAFs with only a few levels can represent both local and global shape features very well, and describe the contour hierarchically and reliably. Then MIAFs are used to derive the effective FD for shape retrieval. The Fourier descriptor based on MIAFs is very compact, and presents good and stable retrieval performance. In this paper, a multi-scale shape signature, namely multi-level included angle functions (MIAFs), is presented to further promote the shape retrieval performance of the FD.
1 Multi-Level Included Angle Functions
In this section, we propose the MIAFs. A shape contour after sampling can be expressed by an ordered set of pointsC={pi=(xi,yi)}, fori=1,2,…,M, wherexiandyirepresent the coordinates of the pointpi, andMis the number of contour points. The length of the contour is denoted byL, which is defined as the number of the contour points in this paper.
The MIAFs can be obtained through the following steps. For each pointpion the shape contour, we can locateK(Kis a positive integer) points orderly by tracing the contour in the forward direction, which satisfy that the arc length betweenpiand thek-th point is equal to (2k+1-2k-1)L/2K+2, fork=1,2,…,K. Then in the reverse direction, otherKpoints can be located on the contour, satisfying the similar constraint. 2Kneighbor points are located totally in such a way. And a pair of line segments can be obtained by connecting pointpiand two neighbor points which have equal arc length from pointpito them, respectively. There areKpairs of line segments in total. Fig.1(a) indicates that six pairs of line segments are formed whenKis set to be six, and Fig.1(b) shows one of the included angles in Fig.1(a).

Fig.1 Contour partitions and included angle. (a) Illustration of paired line segments based on unequal-arc-length partitions of the contour; (b) Illustration of included angle
The included angleθikbetween thek-th pair of line segments can be calculated according to the law of cosines. With a specific starting pointp1of the shape contour, the arc length betweenp1and each pointpiis unique, and the correspondingKincluded angles,θik(k=1,2,…,K), change according topi. Therefore,θikcan be viewed as a function of the arc length. Then for contourC, a set of included angle functions can be expressed asΨ={θ1,θ2,…,θK}, whereθk={θ1k,θ2k,…,θMk}, and denoted as MIAFs.
The MIAFs are clearly invariant under translation and rotation, because the MIAFs are defined directly on contour points and for each point on the shape contour the included angles do not change while rotating or translating the contour. And the MIAFs are also scale invariant. For a given scaling factor denoted as Sf, the lengths of all the line segments change in the same proportion when the contour is scaled. And the proportion Sf is removed during the calculation of included angles, so the MIAFs remain unchanged.
But for different starting points, MIAFs will change subsequently, and the matching process in shape retrieval will become complicated in this case. To eliminate the impact caused by different starting points, the Fourier transform is applied on MIAFs.
2 MIAFs-Based Flourier Descriptor (MIAFD)
The Fourier transform is applied after the MIAFs are extracted to make them independent from the starting point. We resample each original shape contour with equivalent intervals before the implementation of the fast Fourier transform (FFT) in order that the points numberM=2n, wherenis a positive integer. For an included angle functionθkinΨ, whereθk={θ1k,θ2k,…,θMk} andk=1, 2,…,K, the FFT for the function is given as
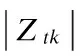
The similarity between two shapes can be determined by the Manhattan distance (MD) metric.
3 Experimental Testing and Results Comparison
To evaluate the effectiveness of the proposed MIAFD, the retrieval tests are conducted on three databases, the MPEG-7 Set B database, the Kimia-99 database, and the Swedish leaf database. Details about these databases can be seen in Refs.[11-13]. And the retrieval results are measured using precision and recall curve. The following experiments are implemented using one computer with a Pentium 3.07 GHz CPU, and Matlab (version 7.9) is used as programming tool.
In our retrieval experiments, the number of the sampling points for each shape contour is 256, and the value of parameterKis set to be 6. In each level, seven low-frequency Fourier features are used for retrieval. This indicates that the total number of coefficients used for the MIAFD is 42.
3.1 Comparisons of MIAFD and other FDs
The proposed method is compared with other four typical Fourier descriptors, including widely used FDs derived from angular radius function (ARF)[8], PAF[6], FPD[5], and AHRC[7]. For all the four Fourier descriptors, the total number of features used is set to be 42 in our experiment, which is a suitable value according to Refs.[4,6-7].
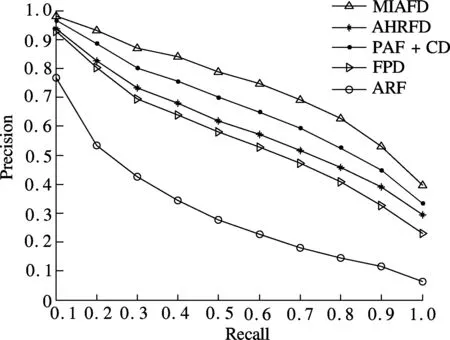
Fig.2 shows the average precision-recall plots using the MPEG-7 Set B database, the Kimia-99 database and the Swedish leaf database.
Fig.2(a) shows that among the competing FDs, the highest precision is reached at each recall level by our method on the MPEG-7 Set B database. For example, when the recall value is 50%, the precision of the MIAFD is higher than that of PAF+CD, the second top descriptor, by 9% and the AHRFD by nearly 17%. The MIAFD also achieves better retrieval result than the other four FDs on the Kimia-99 database and the Swedish leaf database. From Figs.2(b) and (c), we can see that the proposed method achieves much higher precision at each level of the recall value than the other four functions.
To compare the computational complexity of the MIAFD with other FDs, the time required for feature extraction and shape matching is reported for each FD on the MPEG-7 database. In our experiments, feature extraction was implemented for all 1 400 images, and then each shape in the database was taken as a query for each FD. The experiment was repeated 20 times for each FD. The average time required for the feature extraction of one shape and the matching time of one query is shown in Tab.1.
As can be seen from Tab.1, the time that one query shape requires to complete the matching stage for each FD is almost the same. For the feature extraction stage, 18.036 ms is taken for one shape on average using the MIAFD, which is less than that using the FPD and a little more than those using the AHRFD and the PAF+CD. These results show that the MIAFD is competitive in complexity compared with these methods.
3.2 Result comparisons of MIAFD with other shape descriptors
To obtain a comprehensive comparison, the proposed descriptor is also compared with six other notable commonly used or recently proposed descriptors. These shape descriptors are the tensor scale descriptor with influence zones (TSDIZ)[14], the angle scale descriptor (ASD)[10], the SCHT-based shape descriptors (SCHDs)[15], the contour points distribution histogram descriptor (CPDH)[1], the generic Fourier descriptor (GFD)[16],and the curvature-based Fourier descriptor (CBFD)[17]. These descriptors are adopted for the comparison because it has recently been shown that they are efficient and effective techniques for shape retrieval on the standard shape dataset[1,10,14-17].
(a)

(b)
(c)Fig.2 Precision-recall curves of different FD methods. (a) On MPEG database; (b) On Kimia-99 database; (c) On Swedish leaf database

Tab.1 Processing time required for feature extraction and matching stage using FDs ms
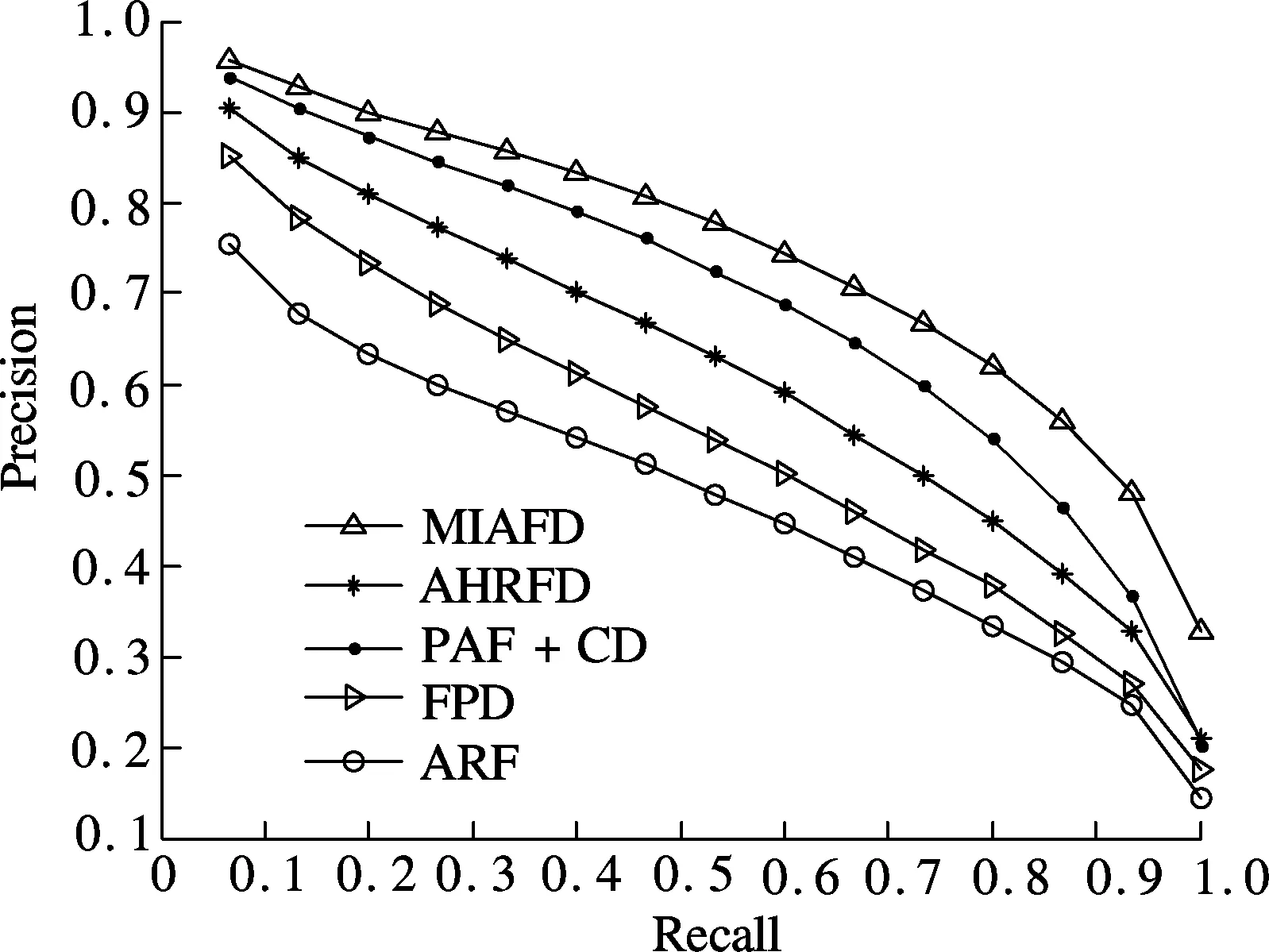
In comparison with these notable approaches, the MIAFD achieves excellent performance. Fig.3 shows the precision-recall plots of the MIAFD, GFD, CPDH, ASD, CBFD, TSDIZ and SCHDs on the standard MPEG-7 database. The precision and recall data of the CPDH, GFD, CBFD, ASD, TSDIZ and SCHDs come from Refs.[1,10,14-17], respectively. It is noted that these results were obtained with optimal parameters. From Fig.3 it is clear that the precision of the CPDH, GFD, CBFD, ASD, TSDIZ and SCHDs at each level of recall is much lower than that of the proposed technique. It is obvious that the performance of the MIAFD is very promising.

Fig.3 Precision-recall curves of the MIAFD, CPDH, GFD, ASD, CBFD, TSDIZ and SCHDs
We also compare the computational complexity of the MIAFD with that of the ASD. We re-implemented the ASD method on the MPEG-7 database according to Ref.[10]. Feature extraction is implemented for all 1 400 images and the first 400 shapes in the MPEG-7database are taken as queries. The average time required for the feature extraction of one shape and the matching time of one query is given in Tab.2. As seen in Tab.2, the MIAFD has a great advantage over the ASD in the computational complexity.

Tab.2 Processing time required for feature extraction and matching stage using MIAFD and ASD ms
4 Conclusion
We propose the MIAFs to describe shape contour hierarchically and reliably. The MIAFs are based on the unequal-arc-length partitions of the contour and can describe shape contour from coarse to fine at different levels. The MIAFs are inherently invariant under translation, rotation and scaling. The MIAFs-based Fourier descriptor (MIAFD) is tested on the MPEG-7 Set B database, the Kimia-99 database and the Swedish leaf database. The experimental results demonstrate that the proposed method can be very compact and present better retrieval performance than other FDs. The reason for the superior retrieval performance is that the proposed MIAFD method can well capture the hierarchy information ranging from global to local variations of shape. Moreover, the comparisons with the other six notable shape descriptors indicate that our method has remarkable retrieval performance.
[1]Shu X, Wu X J. A novel contour descriptor for 2D shape matching and its application to image retrieval [J].ImageandVisionComputing, 2011, 29(4): 286-294.
[2]Wang M, Li F, Wang M. Collaborative visual modeling for automatic image annotation via sparse model coding [J].Neurocomputing, 2012, 95(1): 22-28.
[3]Zhang D S, Lu G J. Review of shape representation and description techniques [J].PatternRecognition, 2004, 37(1): 1-19.
[4]Zhang D S, Lu G J. Study and evaluation of different Fourier methods for image retrieval [J].ImageandVisionComputing, 2005, 23(1): 33-49.
[5]El-ghazal A, Basir O, Belkasim S. Farthest point distance: a new shape signature for Fourier descriptors [J].SignalProcessing:ImageCommunication, 2009, 24(7): 572-586.
[6]Wang B. Shape retrieval using combined Fourier features [J].OpticsCommunications, 2011, 284(14): 3504-3508.
[7]Wang B. Shape description using arc-height radius complex function [J].ActaElectronicaSinica, 2011, 39(4): 831-836. (in Chinese)
[8]Kunttu I, Lepistö L. Shape-based retrieval of industrial surface defects using angular radius Fourier descriptor [J].IETImageProcessing, 2007, 1(2): 231-236.
[9]Arica N, Yarman V F T. Bas: a perceptual shape descriptor based on the beam angle statistics [J].PatternRecognitionLetters, 2003, 24(9/10): 1627-1639.
[10]Fotopoulou F, Economou G. Multivariate angle scale descriptor for shape retrieval[C]//SignalProcessingandAppliedMathematicsforElectronicsandCommunicationsWorkshop. Cluj-Napoca Romania, 2011: 26-28.
[11]Latecki L J, Lakamper R, Eckhardt T. Shape descriptors for non-rigid shapes with a single closed contour[C]//IEEEConferenceonComputerVisionandPatternRecognition. Hilton Head Island, SC, USA, 2000: 424-429.
[12]Sebastian T B, Klein P N, Kimia B B. Recognition of shapes by editing their shock graphs [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2004, 26(5): 550-571.
[13]Xu G Q, Mu Z C, Nan B F. Shape retrieval using improved arc-height function[C]//2012InternationalConferenceonWaveletAnalysisandPatternRecognition. Xi’an, China, 2012: 73-77.
[14]Andaló F A, Miranda P A V, Torres R S, et al. Shape feature extraction and description based on tensor scale [J].PatternRecognition, 2010, 43(1): 26-36.
[15]Wang B, Wu J S, Shu H Z, et al. Shape description using sequency-ordered complex Hadamard transform [J].OpticsCommunications, 2011, 284(12): 2726-2729.
[16]Zhang D S, Lu G J. Shape-based image retrieval using generic Fourier descriptor [J].SignalProcessing:ImageCommunication, 2002, 17(10): 825-848.
[17]El-ghazal A, Basir O, Belkasim S. Invariant curvature-based Fourier shape descriptors [J].JournalofVisualCommunicationandImageRepresentation, 2012, 23(4): 622-633.
基于多级夹角函数的傅里叶形状描述子
徐国清 穆志纯 徐 烨
(北京科技大学自动化学院, 北京 100083)
为了描述形状由全局信息到局部变化的层次信息,提出一种有效的形状签名,即多级夹角函数.多级夹角函数具有内在的旋转、平移和缩放不变性.对轮廓上每一点,其多级夹角函数通过轮廓的非等弧长分割所得的成对线段计算得到.然后利用多级夹角函数推导出傅里叶描述子,以进行高效的形状检索.使用标准的性能评价方法对所提出的描述子在3个形状图像库上进行了测试,包括MPEG-7图像库、Kimia-99图像库和Swedish树叶图像库.形状检索实验结果表明,基于多级夹角函数的傅里叶描述子优于已有的傅里叶描述子,且具有较低的计算复杂度.与其他类型的形状描述方法相比,所提出的描述子在相同查全率时具有最高的查准率,证明了该描述子的有效性.
形状描述;图像检索;多级夹角函数;傅里叶描述子
TP391
The National Natural Science Foundation of China (No.61170116, 61375010, 60973064).
:Xu Guoqing, Mu Zhichun, Xu Ye. Shape retrieval using multi-level included angle functions-based Fourier descriptor[J].Journal of Southeast University (English Edition),2014,30(1):22-26.
10.3969/j.issn.1003-7985.2014.01.005
10.3969/j.issn.1003-7985.2014.01.005
Received 2013-05-28.
Biographies:Xu Guoqing (1986—), male, doctor; Mu Zhichun(corresponding author), male, professor, mu@ies.ustb.edu.cn.
 Journal of Southeast University(English Edition)2014年1期
Journal of Southeast University(English Edition)2014年1期
- Journal of Southeast University(English Edition)的其它文章
- Speech emotion recognitionusing semi-supervised discriminant analysis
- Performance analysis of ammonia-water absorption/compression combined refrigeration cycle
- Optimization of cross-coupling reaction for synthesis of antitumor drug vismodegib
- Flexural behaviors of FRP strengthened corroded RC beams
- Notes on well-posedness for the b-family equation
- Icon memory research under different time pressures and icon quantities based on event-related potential
