Speech emotion recognitionusing semi-supervised discriminant analysis
Xu Xinzhou Huang Chengwei Jin Yun Wu Chen Zhao Li,3
(1Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Physical Science and Technology, Soochow University, Suzhou 215006, China)(3Key Laboratory of Child Development and Learning Science of Ministry of Education, Southeast University, Nanjing 210096, China)
Speech emotion recognitionusing semi-supervised discriminant analysis
Xu Xinzhou1Huang Chengwei2Jin Yun1Wu Chen1Zhao Li1,3
(1Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Physical Science and Technology, Soochow University, Suzhou 215006, China)(3Key Laboratory of Child Development and Learning Science of Ministry of Education, Southeast University, Nanjing 210096, China)
Semi-supervised discriminant analysis (SDA), which uses a combination of multiple embedding graphs, and kernel SDA (KSDA) are adopted in supervised speech emotion recognition. When the emotional factors of speech signal samples are preprocessed, different categories of features including pitch, zero-cross rate, energy, durance, formant and Mel frequency cepstrum coefficient (MFCC), as well as their statistical parameters, are extracted from the utterances of samples. In the dimensionality reduction stage before the feature vectors are sent into classifiers, parameter-optimized SDA and KSDA are performed to reduce dimensionality. Experiments on the Berlin speech emotion database show that SDA for supervised speech emotion recognition outperforms some other state-of-the-art dimensionality reduction methods based on spectral graph learning, such as linear discriminant analysis (LDA), locality preserving projections (LPP), marginal Fisher analysis (MFA) etc., when multi-class support vector machine (SVM) classifiers are used. Additionally, KSDA can achieve better recognition performance based on kernelized data mapping compared with the above methods including SDA.
speech emotion recognition; speech emotion feature; semi-supervised discriminant analysis; dimensionality reduction
Speech emotion recognition (SER) has become a popular research field[1-8]since its combination of speech signal processing, pattern recognition and machine learning. It is widely admitted that some kinds of low-dimensionality manifold structures or subspaces lie in common speech emotion feature space. Additionally, the dimensionality of SER features usually turns to be relatively high using the proposed features[1-7]. Therefore, dimensionality reduction methods play an important role in SER, which can reduce the computational complexity and raise the recognition rate.
In the current research, some manifold-based methods combined with supervised information are proposed to discover the underlying sample space structures of speech emotion signal[6-7]. Meanwhile, subspace learning including manifold learning, for instance, LLE[9], Isomap[10], LE(LPP)[11-12], MLE[13], LDP[14]etc., as well as some unified frameworks[15-16]of them are proposed to combine discriminant analysis, manifold learning and least square problems. Most of them can provide efficient ways to solve dimensionality reduction or some other problems in machine learning and the computer vision field. In these methods, semi-supervised discriminant analysis(SDA)[17], which avoids using only a single embedding graph, makes discriminant information andk-nearest neighbor information together to achieve a better training form for the dimensionality reduction stage.
In this paper, based on SDA, a speech emotion recognition method with the parameters optimized by validation sets is proposed to meet high recognition rates for speech emotion from different speakers. Then, kernel SDA (KSDA) is also adopted based on kernelized data mapping of SDA. We input original speech emotion features into SDA and KSDA. These original features come from recent research. Feature selection methods and SVD described in Ref.[12] can be adopted, since there are many redundant features and the dimensionality of the original feature sometimes exceeds the number of training samples.
1 Methods
1.1 Speech emotion features
The original speech emotion features adopted here are mainly composed of two kinds of features, prosodic features and acoustic quality features. Prosodic features[5], which include pitch, energy of voiced segments, durance features etc., can reflect the changes and overall characteristics of an utterance. Acoustic quality features, which come from frame acoustic features, generally describe the timbre of an utterance.
Here, these features are classified according to different extraction sources. The stage of feature extraction comes after the preprocessing stage, which includes pre-emphasis and enframing. The features adopted in this paper are listed below. The statistics here include maximum, minimum, mean, median, standard deviation and range of an utterance formed by frames.
1) Energy features[2-6]Statistics, the first-order and second-order jitter of the energy sequence; statistics of its first-order and second-order difference sequence; statistics, the first-order and second-order jitter of the energy sequence, with three different frequency bands respectively.
2) Pitch(F0) features[1-7]Statistics, the first-order and second-order jitter of the pitch sequence; the statistics of its first-order and second-order difference sequence; the slope of the voiced-frame sequence.
3) Zero-cross rate features[3]Statistics of zero-cross rate sequence and its first-order and second-order difference sequence.
4) Durance features[1-3,5-6]The number of voiced and unvoiced frames and segments; the longest duration of voiced and unvoiced segments; the ratio of the number of unvoiced to voiced frames; the ratio of the number of unvoiced to voiced segments; the speech rate.
5) Formant (F1, F2, F3) features[2-3,5-7]Statistics of formant frequency sequence and bandwidth sequence; their first-order and second-order difference sequence; the first-order and second-order jitter of the formant frequency sequence.
6) MFCC features[2-3]Statistics of MFCC sequences and their first-order difference sequence.
According to the feature extraction methods, the feature vectors of a speech emotion recognition utterance have a dimensionality of 408.
1.2 Semi-supervised discriminant analysis and its un-ified forms
The methods of SDA come from the idea of RDA(regularized discriminant analysis), which aims to solve the problem of a small number of training samples. Ak-nearest neighbor term in SDA is introduced to replace the former regularize term in RDA. The original form of SDA and RDA is as
(1)
whereSt=Sb+Sw;Swis the within-class scatter matrix, whileSbis the between-class scatter matrix, as described in LDA[18]. Parameterτ≥0, controlling balance between different kinds of information.L=D-Sis the Laplacian matrix ofS, where the element of rowiand columnjinSandDis
(2)
Thus,asproposedinLPP[12]andLE[11],J(a) in SDA is
2aTX(D-S)XTa=2aTXLXTa
(3)
In the form of SDA, the additional term based on existing LDA is used to control the balance between supervised label information and the nearest neighbor information of training samples. It can be seen as a combination form of LDA and a similar form of LPP. According to the graph embedding framework proposed by Yan[15], the graph embedding form of SDA is shown as
(4)
whereDIandDPare the diagonal matrices with each diagonal element representing the corresponding node degrees ofWIandWP, respectively;ec∈RN×1is the column vector with the elements, which are corresponding to emotion classc, being equal to 1, otherwise the elements are equal to 0;ncis the number of samples in classc;Ncis the number of classes.
For supervised SDA (all the training samples are labeled) and semi-supervised situation of SDA, the adjacency matrices of intrinsic and penalty graphs are shown as
(5)
(6)
Tomaketheparameterτbetween 0 and 1, we can let the two graphs simultaneously be divided byτ+1.
By changing the linear form of data mapping into RKHS[18], we can draw supervised KSDA in graph embedding according to Eqs.(4) and (5). Then, the mapping in the new space is performed. The form is shown as
(7)

In Ref.[16], a least-square unified framework is proposed and used for LDA, RDA and their kernelized form. Then, according to the form of SDA in (1) and (4), the unified least-square form for SDA and KSDA can be written as
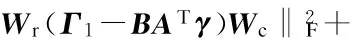

(8)
whereWr=(GTG)-1/2,Wc=I,Γ1=GT,Γ2=PT;Gn×cis the indicator matrix with its elementsgij=1 when sampleibelongs to classj, otherwisegij=0;Pis the approximate decomposition ofSwhereS≈PPT;γ=Xin SDA andγ=φ(X) in KSDA;Adx×kspans the subspace which preserves the correlation betweenΓandγ;Bdd×kspans the column space ofΓ. More information can be seen in Ref.[16].
Eq.(8) can be solved by the form of a generalized eigenvalue problem (GEP). By minimizing the costing function in Eq.(8), the learning of training samples can also be achieved.
1.3 Semi-supervised discriminant analysis for super-vised speech emotion recognition
In the first stage, pre-emphasizing is done by a high-pass filter. Then, each utterance sample is enframed by the Hamming window. After that, the features in section 1.1 are extracted for each utterance sample, which leads to a 408-dimensional feature vector for every sample. We call the above procedure as a priori feature extraction. In contrast, the information of training samples are necessary in the stage of feature selection, SDA and KSDA. We call them as the posteriori feature extraction stage. The Fisher discriminant ratio is chosen as the rule of feature selection. Then, multi-class SVM classifiers are used for the dimension-reduced samples in the final classification stage.
Various kinds of classifiers can be adopted for the classifying stage of SER. The classifier adopted in the experiments here is SVM with linear mapping. Due to the computational complexity of multi-class SVM in optimization, we construct multi-class SVM by voting with 2-class SVM between every 2 classes. However, the voting here may have confusion when the numbers of votes for some classes are the same. To reduce the impact of the problem, when the problem occurs, we only consider the 2-class SVM classifiers related to confusion classes.
Although SDA is approved to be a useful dimensionality reduction algorithm by experiments in Ref.[17], the choice of the parameter between supervised information andk-nearest neighbor information of training samples for supervised situation is not discussed in detail. Owing to convergence problems of the objective function in SDA when using the parameter as an alternating-optimization variable, we enumerate the discrete values of the parameter to achieve relatively better recognition results in every training set, which is divided into training and validation subsets by cross-validation.
2 Experiments
2.1 Corpus and preparations
The corpus adopted in the experiments is the Berlin speech emotion database (EMO-DB), which has 494 samples selected from 900 original ones. 10 professional actors (5 male, 5 female) spoke 10 different short sentences in German. Seven emotion categories including fear, disgust, joy, boredom, neutral, sadness and anger are in the Berlin corpus. The sampling frequency of the database is 16 kHz, while quantization uses 16 bits. Though some deficiencies such as the size of the sample set, the acting factor and language factor exist in EMO-DB, the database is still reliable as a standard corpus for speech emotion recognition research.
The corpus is divided into training and test subsets by different ratios. We repeat the experiments for 20 times or more, with random partitions of training and test sets. The mean values can be calculated based on the repeating experiments. We use 5-fold cross-validation in the training set to choose a relatively appropriate parameter in every dimensionality reduction for SDA or KSDA. In KSDA, three different parameters for three Gaussian kernels, respectively, are used in the experiments. The detailed properties and advantages of kernel methods are stated in Ref.[18].
2.2 Results
The 2-dimensional space of test samples is illustrated in Fig.1, where the spaces of LDA[18], LPP[12], MFA[15]and SDA[17]are represented. It is worth noting that only LPP(see Fig.1(b)) is an unsupervised algorithm. Therefore, the structure of the test samples in LPP seems not so satisfying in speech emotion recognition due to the inaccuracy of the features. It can be seen from Fig.1 that the samples of anger and fear are relatively easier to be separated from other classes in most circumstances.
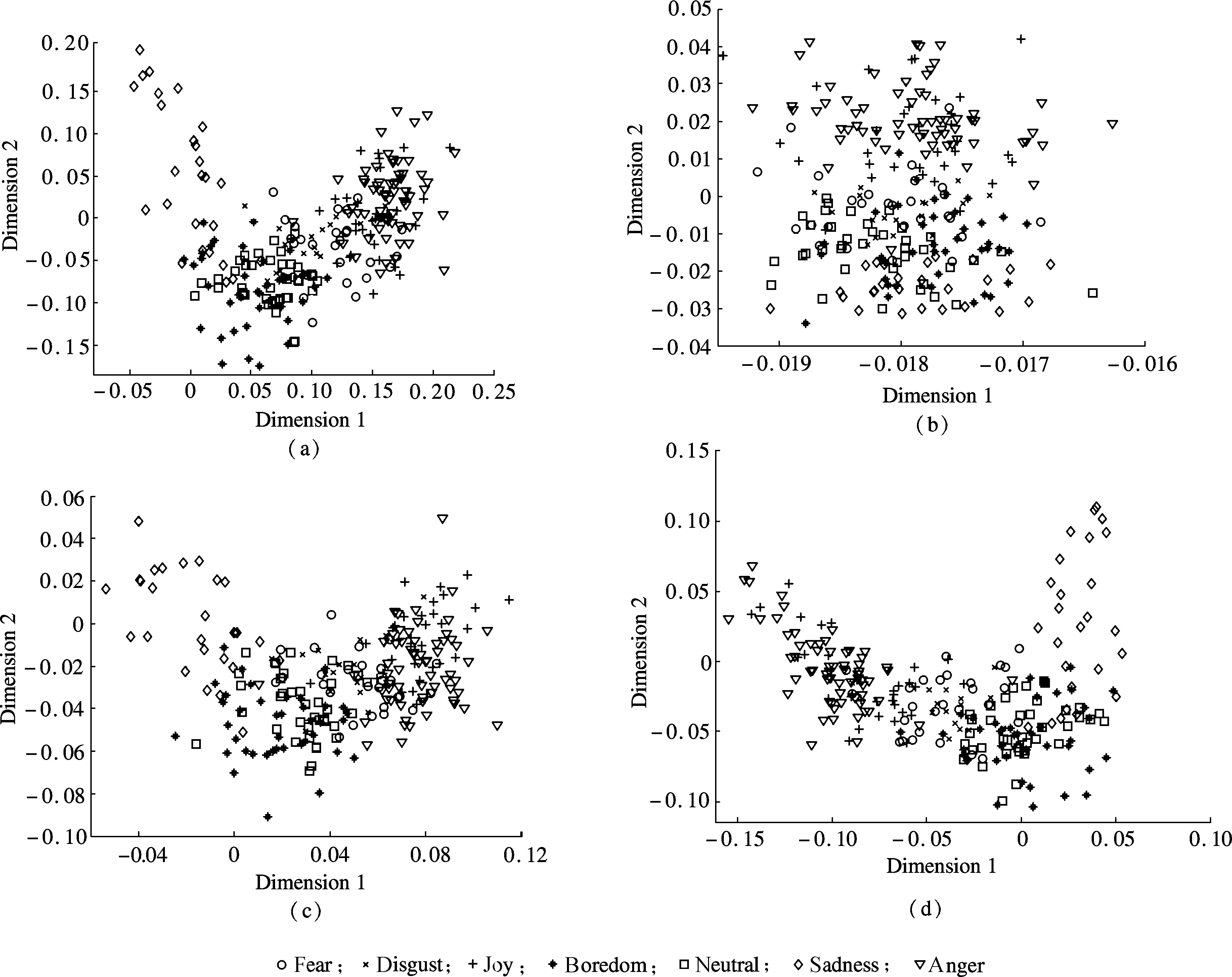
Fig.1 2-dimensional feature space. (a)LDA; (b)LPP; (c)MFA; (d)SDA
The recognition rates of SDA, PCA, LDA, LPP, MFA, kernel1-SDA, kernel2-SDA and kernel3-SDA are shown in Fig.2. The reduced dimensionalities are between 1 and 10 in Fig.2. These dimensionality reduction algorithms are similar under the framework of graph embedding. Generally, the recognition rates increase with the increase of the dimensionality. However, the maximum values of the quotient affect the recognition rates of LDA and SDA when the dimensionality is greater than 6 in the Berlin database. On the contrary, this kind of problem does not exist in PCA, LPP and MFA.
Fig.2(a) shows the recognition rates comparison of SDA, PCA, LDA, LPP and MFA. It is obvious that SDA can achieve better performance even in the condition of supervised dimensionality reduction. Therefore, the combination of embedding graphs can improve the recognition rate of speech emotion features in SER. Then, the algorithms with supervised information (LDA, MFA, SDA) outperform the algorithms without supervised information (PCA, LPP) by a large margin. We can see from the experimental results that the importance of supervised information is very apparent.
As seen in Fig.2(b), KSDA can improve the performance of SDA by nonlinear data mapping. In detail, kernel1-SDA and kernel2-SDA, which are with relatively smaller Gaussian kernel parameters, perform better than kernel3-SDA, whose Gaussian kernel parameter is larger. Based on the experiments, kernel mapping raises the performance of SDA in speech emotion recognition. However, the optimized choice for the parameters of kernels and their combination forms are still worth discussing.
Tab.1 provides the best recognition rates of speech emotion recognition using PCA, LDA, LPP, MFA, SDA and KSDA at different ratios of the number of training samples to test samples. It can be seen that SDA and
KSDA can achieve better performance than PCA, LDA, LPP, MFA and baseline in speech emotion recognition, when the ratios of training to test samples are 5∶5 and 6∶4.
Tab.1 The best recognition rates using the algorithms at different ratios of training to test samples %

RatioBaselinePCALDALPPMFASDAKernel1-SDAKernel2-SDAKernel3-SDA5∶573.466.373.868.173.975.778.478.176.86∶474.266.474.468.474.675.978.678.477.3
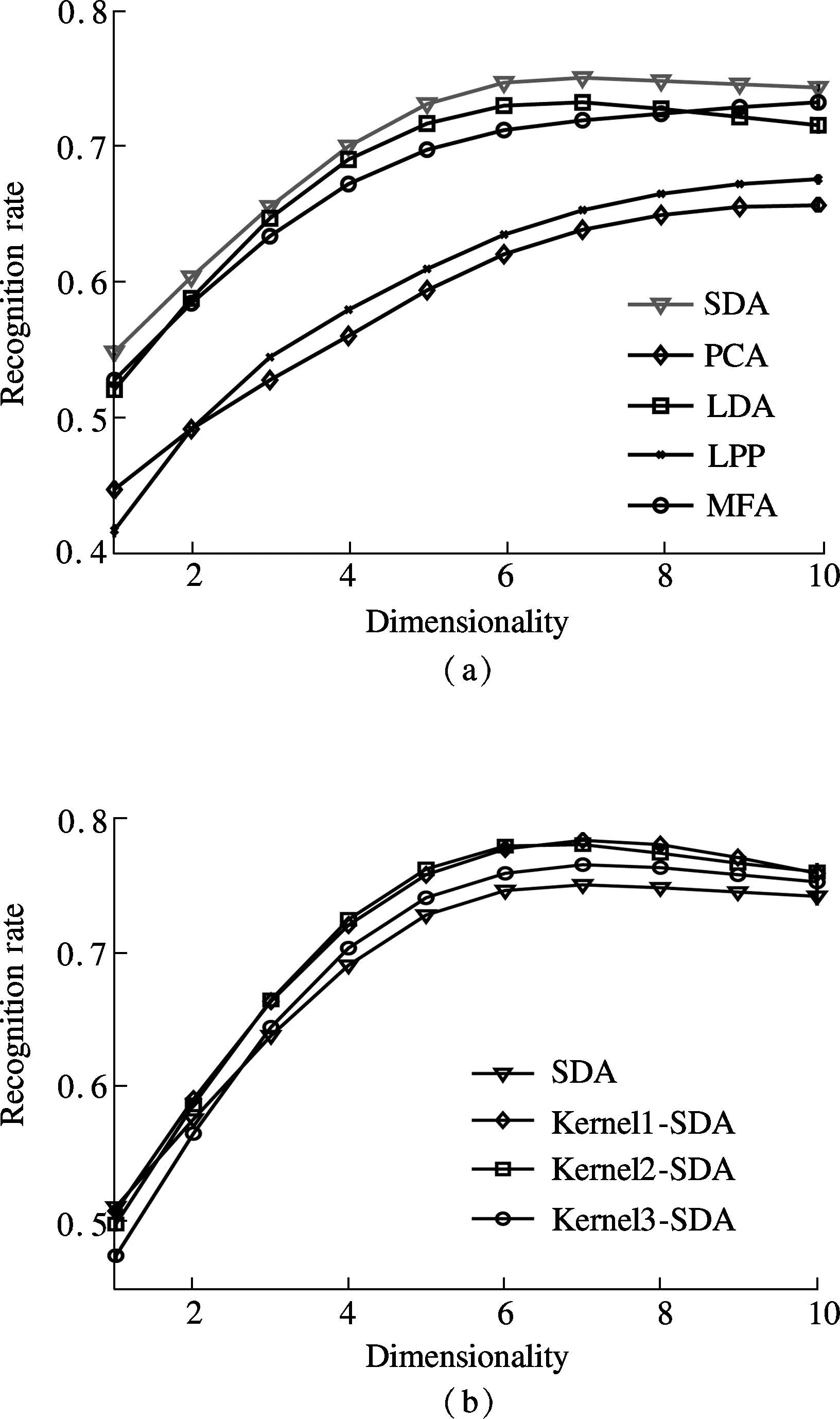
Fig.2 Recognition rates of different methods when the dimensionality changes. (a) SDA, PCA, LDA, LPP and MFA; (b) SDA, kernel1-SDA, kernel2-SDA and kernel3-SDA
3 Conclusion
We use SDA and KSDA with optimized parameters in the dimensionality reduction stage of speech emotion recognition to improve the performance of recognition rates. SDA and KSDA can obviously achieve better recognition capability by only spending extra computational cost in the stage of training. It can be drawn from the experimental results that appropriately combining embedding graphs together is an effective way to obtain better performance than using individual graphs in speech emotion recognition.
However, there are some problems in speech emotion recognition using SDA methods. Optimization by defining a proper cost function is worth researching. Based on the thought of SDA in the framework of graph embedding, more categories of graphs and their optimized combination can be adopted in speech emotion recognition. In addition, more accurate selection of speech emotion features is another direction of future research.
[1]Dellaert F, Polzin T, Waibel A. Recognizing emotion in speech[C]//InternationalConferenceonSpokenLanguage. Philadelphia, PA, USA, 1996, 3: 1970-1973.
[2]Ververidis D, Kotropoulos C. Emotional speech recognition: resources, features, and methods[J].SpeechCommunication, 2006, 48(9): 1162-1181.
[3]Schuller B, Rigoll G. Timing levels in segment-based speech emotion recognition[C]//InternationalConferenceonSpokenLanguage. Pittsburgh, PA, USA, 2006: 1818-1821.
[4]Oudeyer P. The production and recognition of emotions in speech: features and algorithms[J].InternationalJournalofHuman-ComputerStudies, 2003, 59(1/2): 157-183.
[5]Tato R, Santos R, Kompe R, et al. Emotional space improves emotion recognition[C]//InternationalConferenceonSpokenLanguage. Denver, CO, USA, 2002: 2029-2032.
[6]Zhang S Q, Zhao X M, Lei B C. Speech emotion recognition using an enhanced kernel Isomap for human-robot interaction[J].InternationalJournalofAdvancedRoboticSystems, 2013, 10: 114-01-114-07.
[7]You M Y, Chen C, Bu J J, et al. Emotional speech analysis on nonlinear manifold[C]//InternationalConferenceonPatternRecognition. Hong Kong, China, 2006,3: 91-94.
[8]Ayadi M, Kamel M, Karray F. Survey on speech emotion recognition: features, classification schemes, and databases[J].PatternRecognition, 2011, 44(3): 572-587.
[9]Roweis S, Saul L. Nonlinear dimensionality reduction by locally linear embedding[J].Science, 2000, 290(5500): 2323-2326.
[10]Tenenbaum J, de Silva V, Langford J. A global geometric framework for nonlinear dimensionality reduction[J].Science, 2000, 290(5500): 2319-2323.
[11]Belkin M, Niyogi P. Laplacian eigenmaps and spectral techniques for embedding and clustering[C]//AdvancesinNeutralInformationProcessingSystems14. Whistler, British Columbia, Canada, 2002: 585-591.
[12]He X F, Niyogi P. Locality preserving projections[C]//AdvancesinNeuralInformationProcessingSystems15. Whistler, British Columbia, Canada, 2003: 153-160.
[13]Wang R P, Shan S G, Chen X L, et al. Maximal linear embedding for dimensionality reduction[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2011, 33(9): 1776-1792.
[14]Cai H P, Mikolajczyk K, Matas J. Learning linear discriminant projections for dimensionality reduction of image descriptors[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2011, 33(2): 338-352.
[15]Yan S C, Xu D, Zhang B Y, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2007, 29(1): 40-51.
[16]De la Torre F. A least-squares framework for component analysis[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2012, 34(6): 1041-1055.
[17]Cai D, He X F. Semi-supervised discriminant analysis[C]//InternationalConferenceonComputerVision. Rio de Janeiro, Brazil, 2007: 1-7.
[18]Shawe-Taylor J, Cristianini N.Kernelmethodsforpatternanalysis[M]. Cambridge, UK: Cambridge University Press, 2004.
基于半监督判别分析的语音情感识别
徐新洲1黄程韦2金 赟1吴 尘1赵 力1,3
(1东南大学水声信号处理教育部重点实验室,南京 210096) (2苏州大学物理科学与技术学院, 苏州 215006) (3东南大学儿童发展与学习科学教育部重点实验室, 南京 210096)
将基于多个嵌入图组合形式的半监督判别分析 (SDA)以及核SDA (KSDA)应用于全监督的语音情感识别. 在语音信号样本情感成分的预处理阶段, 从样本语段中提取出多种特征及其统计参数, 包括基音、过零率、能量、持续长度、共振峰和 MFCC (Mel频率倒谱系数). 在将样本特征送入分类器之前的维数约简阶段, 使用经过参数优化的SDA或KSDA进行降维. Berlin语音情感数据库上的实验表明,在使用多类SVM分类器时的全监督语音情感识别中, SDA优于其他一些先进的基于谱图学习的维数约简算法, 如LDA, LPP, MFA等, 而KSDA通过核化的数据映射, 能够取得比上述所有算法更好的识别效果.
语音情感识别; 语音情感特征; 半监督判别分析; 维数约简
TN912.3
s:The National Natural Science Foundation of China (No. 61231002, 61273266), the Ph.D. Programs Foundation of Ministry of Education of China (No.20110092130004).
:Xu Xinzhou, Huang Chengwei, Jin Yun, et al.Speech emotion recognition using semi-supervised discriminant analysis[J].Journal of Southeast University (English Edition),2014,30(1):7-12.
10.3969/j.issn.1003-7985.2014.01.002
10.3969/j.issn.1003-7985.2014.01.002
Received 2013-08-05.
Biographies:Xu Xinzhou (1987—), male, graduate; Zhao Li (corresponding author), male, doctor, professor, zhaoli@seu.edu.cn.
 Journal of Southeast University(English Edition)2014年1期
Journal of Southeast University(English Edition)2014年1期
- Journal of Southeast University(English Edition)的其它文章
- Wavelet transform and gradient direction based feature extraction method for off-line handwritten Tibetan letter recognition
- Analyses of unified congestion measures for interrupted traffic flow on urban roads
- Conditional autoregressive negative binomial model for analysis of crash count using Bayesian methods
- Design and analysis of traffic incident detection based on random forest
- Biodegradation of microcystin-RR and-LR by an indigenous bacterial strain MC-LTH11 isolated from Lake Taihu
- Inverse kinematic deriving and actuator control of Delta robot using symbolic computation technology
