基于突变理论的单根土钉抗拔极限承载力计算

蔡函珂，张远芳，王　月，孙　勇

(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)



基于突变理论的单根土钉抗拔极限承载力计算

蔡函珂，张远芳，王月，孙勇

(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)

摘要:土钉抗拔极限承载力的计算是土钉结构设计的关键。以往的土钉抗拔力的计算往往只通过力学平衡分析法进行计算，但是土钉的作用机理是相当复杂的，单纯具体的力学分析很难满足设计所需的计算公式。通过建立势能函数方程，运用突变理论原理，避开具体的力学分析，计算解析得出土钉抗拔极限承载力的计算公式。运用该公式可以更好的实现安全节能的设计理念。

关键词:基坑；土钉支护；突变理论；抗拔强度

土钉支护[1-2]的独特优越性，使得土钉支护在基坑工程中普遍应用[3]。在土钉支护结构设计中土钉抗拔强度是一个重要的设计参数，如何确定土钉抗拔极限承载力是其设计的一个关键所在。

近年来，许多学者对其进行研究，例如，秦四清等[4]在对土钉抗拔机理研究中得出，钉土间的摩阻力发挥作用的前提是钉土之间产生相对位移，随着相对位移的增加摩阻力不断增大直至达到临界值。丁振明等[5]在此基础上提出了土体自承作用与钉土作用两个全新的概念，将土钉抗拔极限承载力分为自承作用与钉土作用两部分。研究得出的抗拔力都与上覆土压力直接相关。但是，苏立君等[6]试验研究表明，钻孔灌注型土钉的抗拔强度与上覆土的土压力大小无关，与喷浆压力和土样饱和度有关。因此可以看出，学者们对土钉抗拔作用机理的认识还没有形成共识，仍处在探讨阶段。

本文通过被动区土钉的受力分析，建立其能量方程，结合突变理论原理推求土钉抗拔极限承载力的解析解。

1　土钉支护结构破坏形式与力学模型

1.1土钉支护结构的破坏形式

陈肇元、崔京浩等[7]认为:土钉支护结构破坏形式分为体外破坏(图1)与体内破坏(图2)。大量工程实践表明[8-9]还没有发生过体外破坏的情况，也没有出现过由于面层体系的破坏而导致整个支护体系破坏的情况，因此本文只讨论体内破坏情况下单根土钉抗拔极限承载力的确定，即破坏面全部穿过加固土体的内部，如图2。

图1体外破坏

图2体内破坏

1.2土钉支护结构的力学模型

土钉抗拔力主要由被动区的钉土摩擦力与钉土粘聚力提供，因此在研究土钉抗拔极限承载力时取被动区内的土钉为研究对象，见图3、图4，并假设:(1)土钉抗拔力全部由钉土摩擦力与钉土黏聚力提供。(2)土钉在支护过程中只受拉力作用。(3)土钉(由带肋钢筋、钢管等与注浆材料组成，注浆材料可为水泥浆或水泥砂浆且强度不低于20 MPa)自身强度足够，受荷过程中不会拉变形。

图3土钉计算参数示意图

图4被动区段土钉受力分析示意图

钉土的摩阻力发挥程度与其相对位移有关，有关学者[10]给出了两者之间的关系:

(1)

σ=γZcosθ

(2)

(3)

(4)

2　土钉的突变模型建立

本文所研究的目标体为土钉的抗拔作用段，即土钉在被动区内的部分，因此取被动区内的土钉段为研究对象，见图4，根据势能增量原理建立其势函数:

(5)

式中:Nu为抗拔段所承受的拔力(kN)；s为抗拔段钉土总相对位移(mm)；D为土钉直径(m)。

对式(5)求导,并令W′=0，得:

(6)

其中:

(7)

×μ·π·D·cosθ·γ

式中:l2为被动区内土钉的长度(m)。

令

则:

(8)

(9)

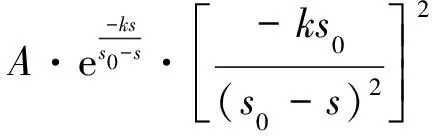
(10)

令W‴=0，得:

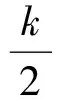
(11)

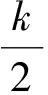
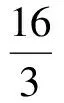
(12)

(13)

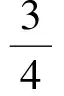
(14)

令

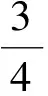
代入(14)得:

W′=y3+ay+b=0

(15)

式(15)即为突变理论模型中尖点模型的标准形式平衡方程，进一步求导得:

W″=3y2+a=0

(16)

式(16)为奇点集的方程，此时的分叉集方程为:

4a3+27b2=0

(17)

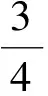
由式(16)解得:

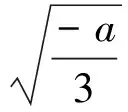
(18)

并可以确定其临界失稳点的位移S*为:

s*=(1-k)·s0

(19)

代入式(8)得:

(20)

所以单根土钉抗拔极限承载力Rk,j为:

(21)

(22)

式中:l2,j为第j根土钉在被动区内的长度(m)；Lj为第j根土钉长度(m)；Rk,j为第j根土钉的抗拔极限承载力(kN)；其他符号含义同上。

3　实例计算分析

3.1工程概况

新疆乌鲁木齐某高层建筑[14-15]基坑主要参数:h=8.2 m，α=90°，θ=0°，γ=20 kN/m3，c=9 kPa，μ=0.3，D=0.1 m，φ=36°，Sh=1.1 m，Sv=1.3 m，支护等级为三级，工程厂区内土层主要为砂质粉土，土钉为成孔注浆土钉，基坑边坡如图5所示，各土钉从地面到坑底编号为1号到6号。

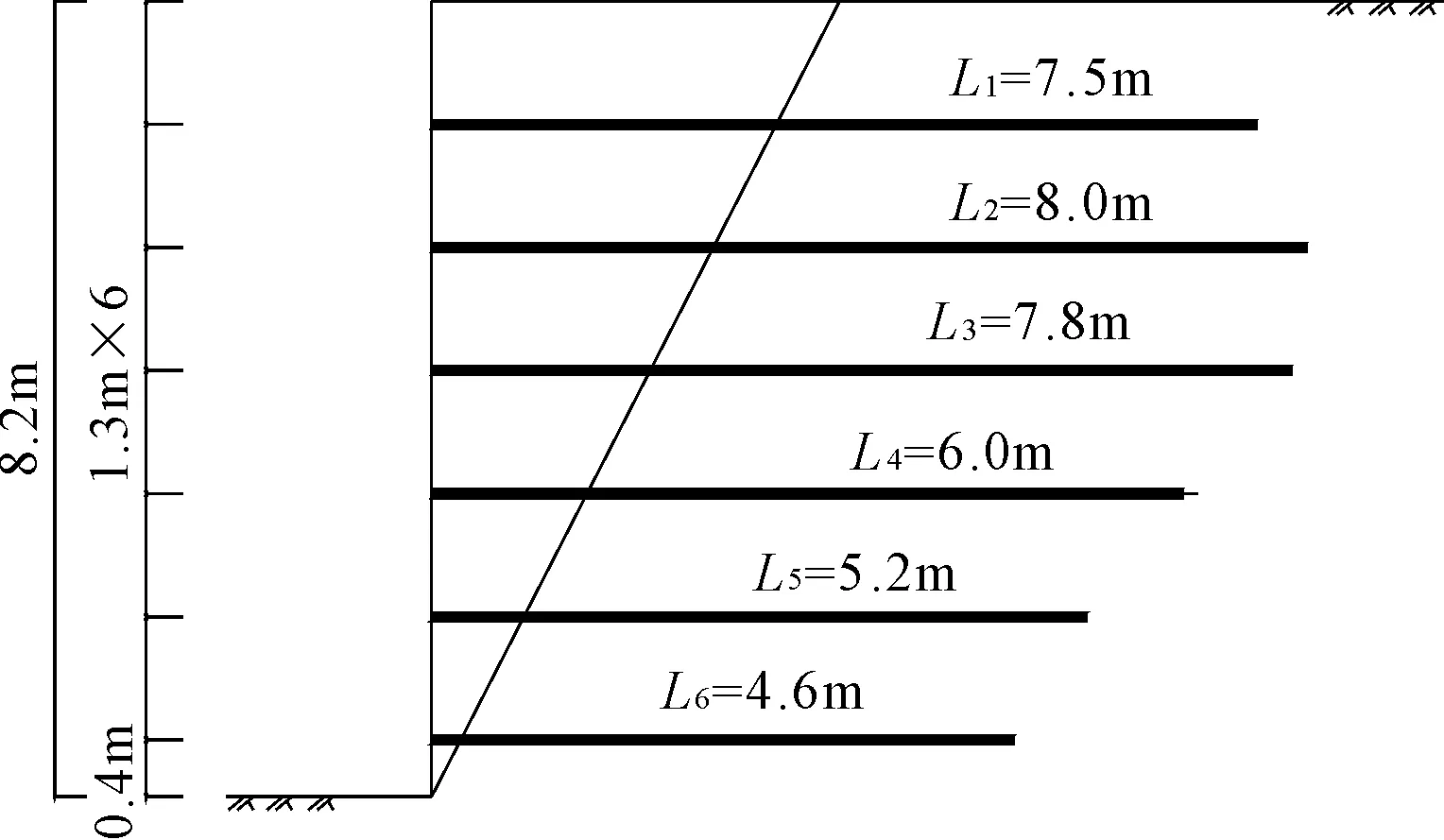
图5土钉墙支护示意图

3.2土钉极限抗拔承载力计算与分析

根据工程提供的数据，结合本文计算方法进行计算，计算结果如表1。

表1　土钉抗拔极限承载力计算值

从图6(按《建筑基坑支护技术规程》(JGJ 120-2012)中规定，以1.4倍的设计安全系数放大实测土钉轴力，观察极限抗拔力计算值是否包围该放大数值曲线)中我们可以清楚的看到土钉抗拔极限承载力随深度的增加而增加，但实测的土钉轴力为中部的受力最大呈凸肚型，并且可以看出土钉抗拔极限承载力远大于其土钉实际轴力，且越到基坑底部土钉极限抗拔承载力计算值与土钉实测轴力相差越大，说明在该实际工程中土钉未完全发挥其抗拔作用，随着深度的增加土钉的安全储备抗拔力逐渐增大，在一定范围内提高了基坑的安全性。

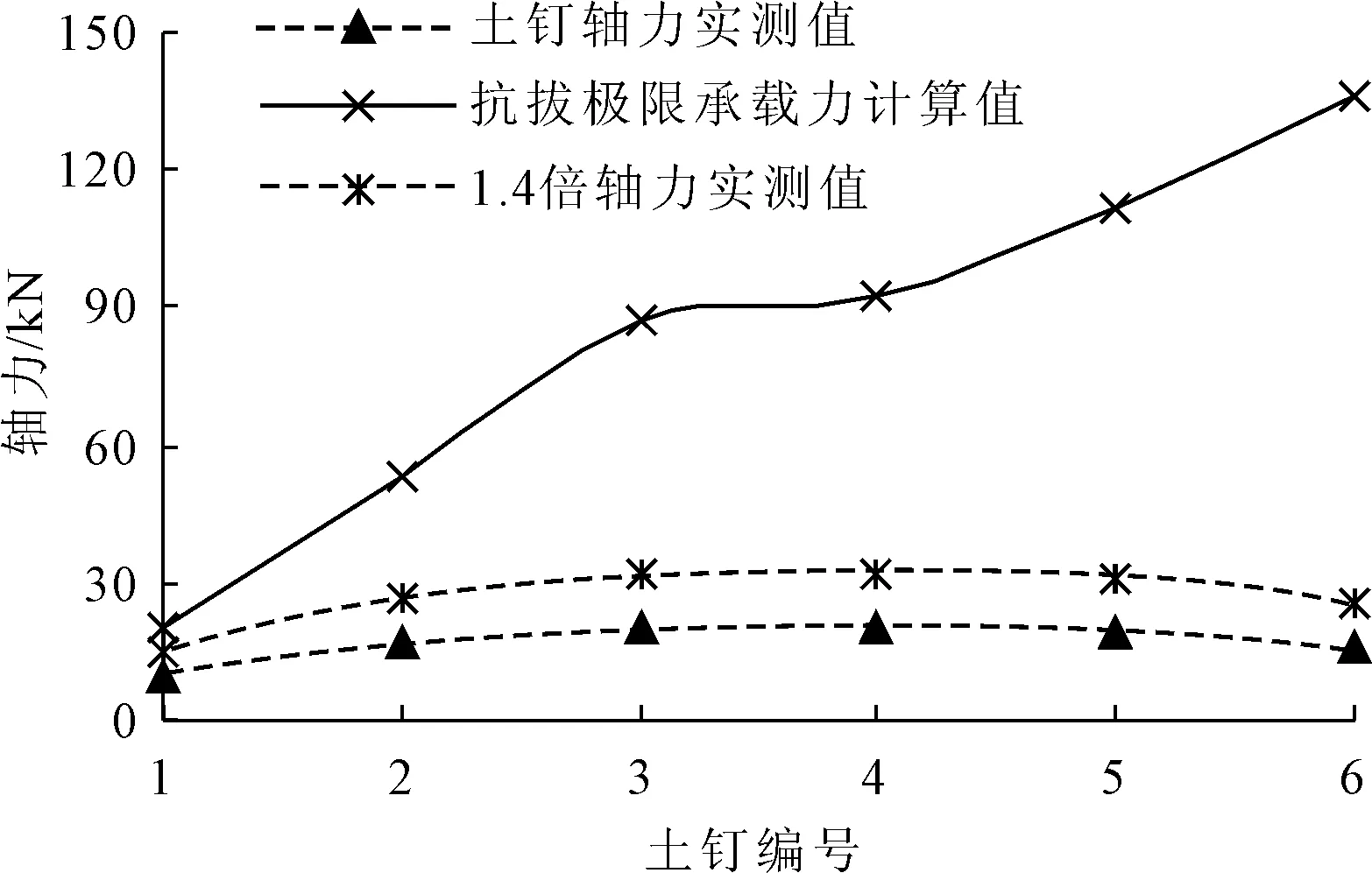
图6土钉抗拔极限承载力计算值与实测

同时可以看出上部的土钉发挥作用较充分(土钉抗拔极限承载力计算值除土钉实测轴力值，所得数值越大，表明土钉发挥较充分)，中下部的土钉只发挥了其中的一小部分的作用。因此在土钉支护设计中中部的土钉可以适当的增加长度，上部、下部土钉的长度可以适当的优化减短，以达到更加经济的设计方案。

4　结　论

(1)土钉的作用机理相当复杂，本文在其公式的推导过程中没有考虑土钉的群锚效应和钉土之间的凝聚力等相关因素，具有一定的局限性，因此该公式还有待进一步完善与验证。

(2)通过数值模拟方法和运用突变理论建立了土钉抗拔极限承载力的计算公式，该计算方法能够计算出土钉抗拔极限承载力，对实际工程设计有一定的指导作用。

参考文献:

[1]Zou Guangdian,Jiang W. Stability analysis of soil nailing based on coupling algorithm of simulated annealing algorithm and random disposal-method of points[J]. Rock and Soil Mechanics，2004,25(1):37-44.

[2]Bahner Eric W,Sirvinskis J. Soil nailing for the WHEDA office building in Madison,Wisconsin[C]//Geo-engineering for Underground Facilities. ASCE,1999:212-230.

[3]姜晓光,杨志银,刘斌.土钉墙支护水平位移计算的简便方法[J].土木工程学报,2010,43(8):121-124.

[4]秦四清,王建党,王清,等.土钉支护机理与优化设计[M].北京:地质出版社,1999.

[5]丁振明,秦四清,刘军,等.土钉支护体系抗拔力机理研究[J].岩土力学,2005,26(11):1799-1802.

[6]苏立君,张宜健,殷建华,等.钻孔灌注型土钉抗拔性能的室内模型试验研究[J].西安建筑科技大学学报:自然科学版，2011,43(3):342-346，366.

[7]陈肇元,崔京浩.土钉支护在基坑工程中的应用[M].北京:中国建筑工业出版社,2000.

[8]钟声.基于突变理论的土钉支护体系的稳定分析研究[D].广州:广州大学,2006.

[9]张贞.突变理论在土钉支护体系中的应用研究[D].西安:西安建筑科技大学,2007.

[10]聂珊利.基于尖点突变理论的摩擦桩竖向承载力分析[D].乌鲁木齐:新疆农业大学,2010.

[11]凌复华.突变理论及其应用[M].上海:上海交通大学出版社,1987.

[12]周燕华.突变理论[M].北京:高等教育出版社,1990.

[13]凌复华.突变理论入门[M].上海:上海科学技术文献出版社,1983.

[14]高盟,张远芳.基于有限元分析的土钉支护优化设计的复合形算法[J].岩土工程学报,2006,28(8):1008-1012.

[15]王广冰,张远芳,高盟,等.基于最小势能原理的土钉支护结构位移解析解[J].岩土工程学报,2010,32(3):415-419.

TheUltimateBearingCapacityofSingleSoilNailPulloutBasedonCatastropheTheory

CAI Han-ke,ZHANG Yuan-fang,WANG Yue,SUN Yong

(CollegeofHydraulicandCivilEngineering,XinjiangAgriculturalUniversity,Urumqi,Xinjiang830052,China)

Abstract:Calculating the ultimate bearing capacity of soil nail pullout is the key design of soil nailing structures. Calculation of soil nail pullout resistance was often carried out by mechanical equilibrium analysis method in the past. However,the mechanism of soil nailing is quite complicated,the analysis alone is not enough to achieve a specific formula that meet the designing need. Here ,through the establishment of the potential energy function equation,using the principle of catastrophe theory,avoiding specific mechanical analysis,the formula of calculating the ultimate bearing capacity of nail pullout resistance was unearthed. This formula is more practical for the design purpose of energy conservation.

Keywords:excavation pit;soil nailing;catastrophe theory;pullout resistance strength

DOI:10.3969/j.issn.1672-1144.2014.05.016

中图分类号:TU473.1+2

文献标识码:A

文章编号:1672—1144(2014)05—0083—04

作者简介:蔡函珂(1987-),男，浙江丽水人，硕士研究生，研究方向为深基坑工程。通讯作者:张远芳(1963—)，女，江苏无锡人，副教授，硕士生导师，主要从事灾害岩土工程研究，岩土工程数值分析和岩土工程及水文地质与工程地质教学与科研工作。

基金项目:新疆水利水电工程重点学科基金资助(xjzdsk-2002-10-05)

收稿日期:2014-04-23修稿日期:2014-05-27