钢筋混凝土核心筒受力性能及其极限承载力分析
薛东智
(陕西建工集团总公司, 陕西 西安 710003)
钢筋混凝土核心筒受力性能及其极限承载力分析
薛东智
(陕西建工集团总公司, 陕西 西安 710003)
摘要:通过合理设计,实现钢筋混凝土核心筒在大震作用下形成良好的屈服机制和破坏模式对于整体结构的抗震性能十分关键。通过对比核心筒不同损伤模式,并利用基于能力设计原理,确定“强墙肢-弱连梁”结构形式为合理屈服机制。根据带翼缘L形单肢剪力墙极限承载力的计算方法,推导出了双肢剪力墙墙肢极限承载力的计算公式。由该极限承载力计算方法,通过实例得到核心筒水平极限承载力和抗倾覆弯矩计算值,并与试验值进行了比较,结果较为吻合,表明在主轴方向,核心筒极限承载力可简化为带翼缘的双肢剪力墙计算理论进行分析。计算结果还表明,连梁在筒体整体抗侧能力中起到很大的作用,连梁的抵抗弯矩占整个试件的40%以上。
关键词:混凝土核心筒;受力性能;损伤模式;能力设计方法;极限承载力
在高层建筑结构中,根据连梁及墙体尺寸,核心筒墙体在平面内可分解为整体墙或联肢剪力墙,目前有关整体剪力墙的受力性能研究较多,试验和理论研究较为丰富[1-5]。但由于连梁和墙肢的耦合作用,联肢剪力墙的受力性能较整体剪力墙有很大不同,这方面的试验及理论研究还较为匮乏[6-9]。在大震作用下,墙肢变形较大,对连梁施加较大的强制性变形,由于连梁和墙肢的耦合作用,对联肢剪力墙结构的抗震性能造成较大影响。在墙肢基于性能的合理设计基础上,连梁成为沿核心筒高度可以稳定耗散地震能量的关键构件。
核心筒决定着整个结构体系的抗震性能,如何控制核心筒形成合理的屈服机制和破坏模式具有重要意义。合理的屈服机制可以使核心筒形成较好耗能分布的破坏模式,提高结构抗震性能,避免因不合理破坏导致结构严重损坏或倒塌。
本文根据能力设计思想分析核心筒合理的损伤模式,由预先设定的屈服模式进行核心筒试件的设计,对所设计混凝土核心筒试件的极限承载力进行验算,并与试验结果进行对比分析,考察核心筒基于能力设计方法的有效性和合理性。同时,由于目前核心筒的承载力计算仍按照剪力墙的承载力计算方法,考虑到核心筒为空间受力,核心筒基于剪力墙承载力计算方法的合理性有待深入研究。本文根据连梁和墙肢受力的工作特点,推导出罕遇地震作用下混凝土核心筒的极限承载力计算公式。
1 核心筒基于能力的设计方法
1.1能力设计原理
能力设计原理最早由20世纪60年代美国学者提出,由新西兰国际著名混凝土及抗震专家Paulay T教授和Park R教授[10]对其进行了系统整理与归纳,并提出了较为完善的设计方法。该方法的主要思想是通过结构主要抗侧力体系的不同构件之间的承载能力差进行控制,明确塑性铰出现位置,并进行仔细的配筋设计以保证具有足够的延性性能,通过预先设定的延性构件在大震下屈服来消耗地震能量,而不利的塑性铰或破坏形式(如脆性破坏)则通过设计使其满足足够的强度,具有充足的能量储备,而维持在弹性和准弹性阶段,一般不出现塑性铰。
1.2核心筒屈服机制和破坏模式
核心筒根据剪力墙墙肢和连梁刚度及尺寸的不同,形成以下几种不同墙肢-连梁分布机制:(1)无连梁模式;(2)强墙肢-弱连梁模式;(3)弱墙肢-强连梁模式;(4)混合耦合模式,其中混合耦合模式由于布置不均匀,在核心筒中较少出现,故较少进行分析。各种组合下的核心筒受力和变形性能有较大差距,屈服机制和破坏模式也各有不同。
文献[11]对各种组合形式的RC框架-剪力墙结构进行了大震作用下的弹塑性时程分析,得到了各自的损伤模式与耗能分布,并对不同损伤模式的抗震性能进行了定性分析。分析结果如下:(1)很弱连梁(或无连梁)损伤模式墙肢损伤较严重,墙肢耗能分布“不可控”;(2)强墙肢-弱连梁损伤模式中连梁、框架梁和墙肢均出现屈服,其中连梁塑性铰发展程度较深,墙肢虽然屈服,但损伤相对于无连梁模式要低很多,结构模式耗能分布“可控”;(3)弱墙肢-强连梁损伤模式中连梁、框架梁和墙肢均出现屈服,其中连梁破坏严重,墙肢相比弱连梁模式损伤更为严重,结构模式耗能分布“不可控”。
1.3基于能力设计原理的核心筒试件设计
由核心筒损伤模式可知,强墙肢-弱连梁核心筒的损伤模式将由连梁和墙肢共同屈服耗能,其中连梁损伤较严重,墙肢损伤较轻,并只发生在底部,上部保持弹性,耗能分布“可控”。综上所述,在进行核心筒设计时,应尽量选择强墙肢-弱连梁的结构形式,从而使核心筒在地震作用下可以形成合理屈服机制。理想的塑性极限状态为首先连梁端部形成稳定耗能的塑性铰,结构此时并未破坏,进而梁铰形成的大变形使墙肢底部也屈服,但屈服程度较小,整体形成机动体制。这样不但从整体上降低了墙肢的损伤程度,较大限度地避免了结构的倒塌,而且降低了震后的维修费用。核心筒理想塑性极限状态符合能力设计思想。
进行基于能力原理的核心筒设计时,在确定好核心筒构件组合模式后,还有以下几个问题需要解决:(1)如何通过各项参数设置实现“强墙肢-弱连梁”模式的形成,但又不至太弱而形成近似无连梁的悬臂墙;(2)如何控制连梁发生以弯曲为主的破坏;(3)如何满足墙肢的强度要求,即在小震下保持弹性,中震下轻破坏,不屈服,大震下虽然运行发生屈服,但屈服程度较小。
对于第一问题,由于核心筒开洞一般较为均匀,布置规则,在平面内可等效为联肢剪力墙,故可通过控制墙肢整体系数和肢强系数来实现剪力墙和连梁的刚度比分配,决定核心筒剪力墙的组合模式[12],其中整体系数α可表示为:
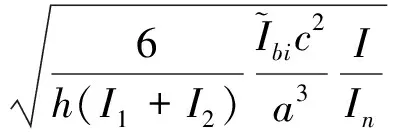
(1)
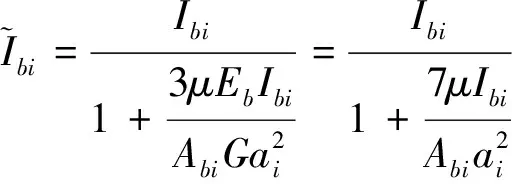
(2)
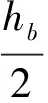
(3)
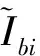
肢强系数定义为:
ζ=In/I
(4)
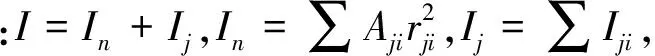
小开口墙和联肢剪力墙的判别条件如下:
小开口墙满足:
α≥10
(5)
ζ=In/I≤[ζ]或IA/I≤[ζi]
(6)
联肢剪力墙满足:
α<10
(7)
ζ=In/I≤[ζ]
(8)
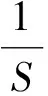
(9)
式中:[ζ]为肢强系数允许值。
以文献[13]中试件CW-1为例进行核心筒墙肢和连梁尺寸确定,使试件满足强墙肢-弱连梁模式。首先进行剪力墙和连梁尺寸初步确定,剪力墙墙肢长度均取600 mm,初步设计连梁跨高比为2.0,连梁净跨取600 mm,则高度取300 mm,墙肢和剪力墙截面宽度均为80 mm,则可进行剪力墙类型判别,通过计算得剪力墙整体系数为α=8.53,ζ=0.653<[ζ]=0.689,故可判断核心筒墙肢和连梁尺寸满足弱连梁要求。
对于第二个问题,设计连梁跨高比为2.0,属于小跨高比,从试验来看,较为容易发生剪切破坏,而使得连梁达不到延性构件的要求,不能充分耗能。如果连梁纵筋配筋率按框架梁进行配置,可能造成连梁受弯承载力过高,构件因斜截面受剪承载力超过剪压比限值而发生受剪破坏[14]。为避免这种情况发生,需要对连梁纵筋配筋率进行相应控制,可由以下步骤进行设计。连梁端部正截面受弯承载力为:

(10)
由文献[15]可知连梁在达到极限承载力之前,约有h/4截面高度没有发生开裂,压力的合力点距受压边缘为h/8,则:

(11)
忽略连梁轴向力,连梁在纵筋屈服时达到的剪力为:V=Mb/(0.5l)=2fyρsbh0(h0-h/8)/l
(12)
如果连梁首先发生弯曲破坏,则需使连梁抗剪承载力大于弯矩引起的剪力。则连梁必须配置足够多的抗剪钢筋以满足受剪承载力的要求。
初步给出纵筋配筋率为0.57%,进行弯矩及剪力计算,并计算箍筋最小需求量,最终配置箍筋为φ4@60,并根据规范要求另设直径为12mm的斜向交叉构造钢筋,则连梁剪力值为:
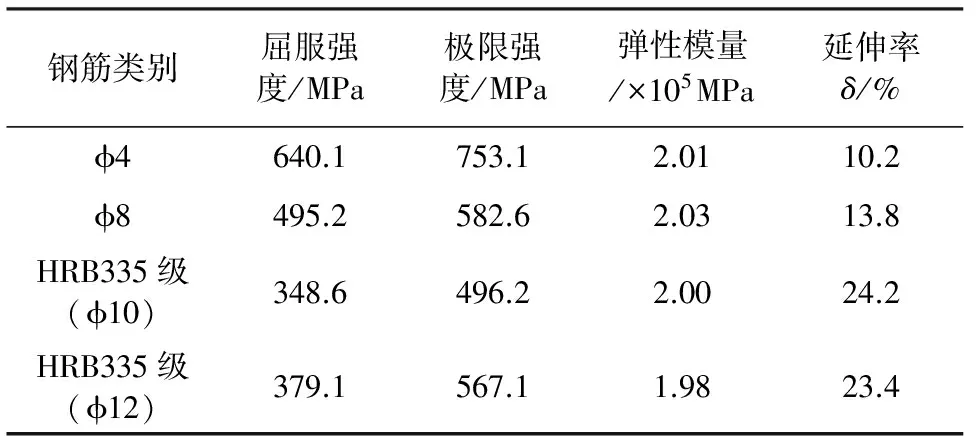
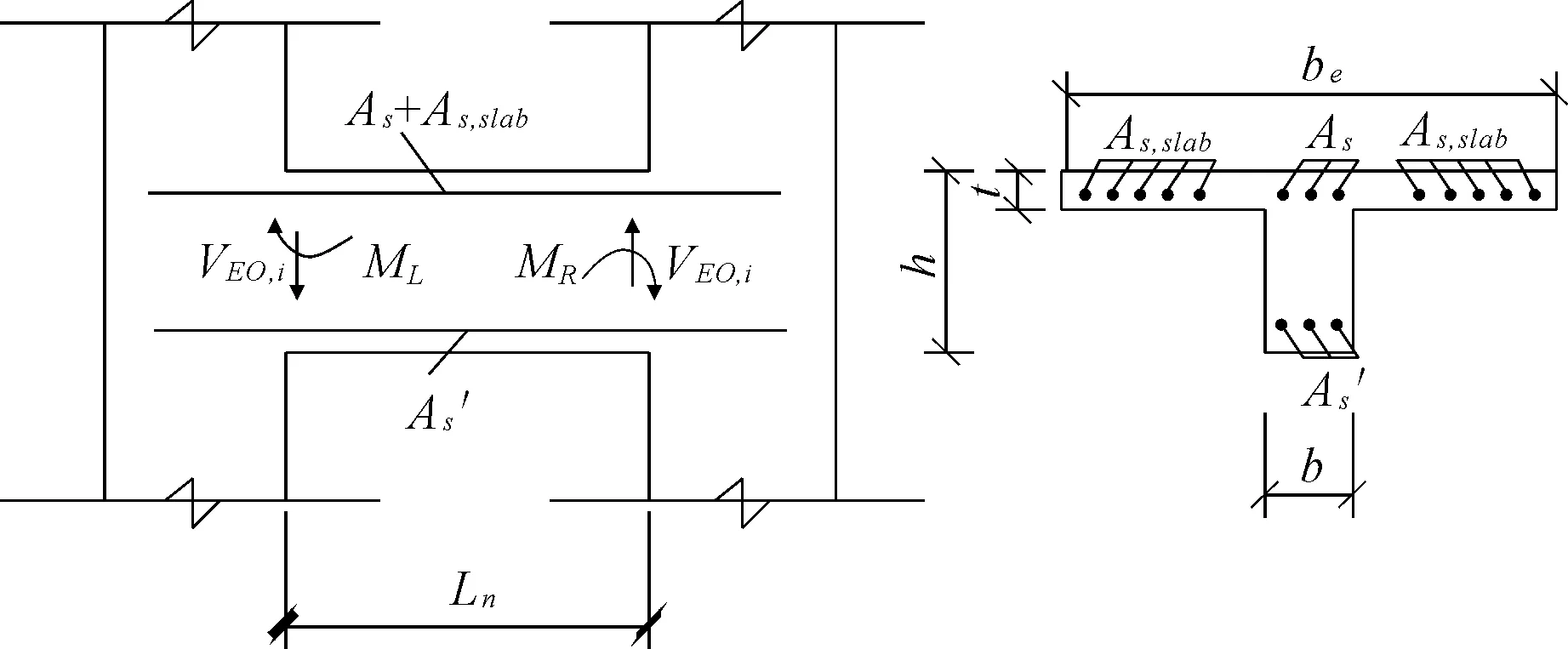
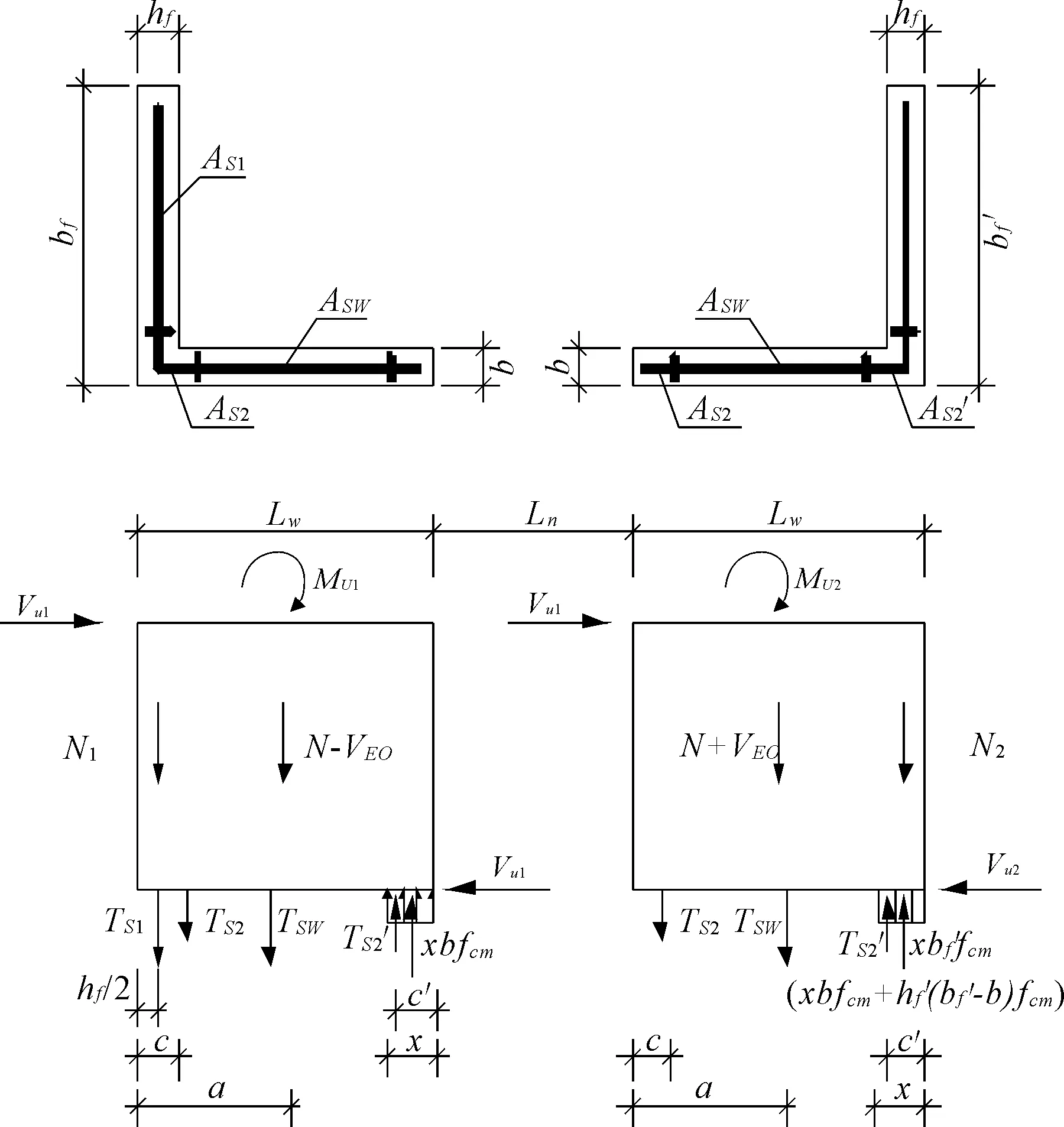
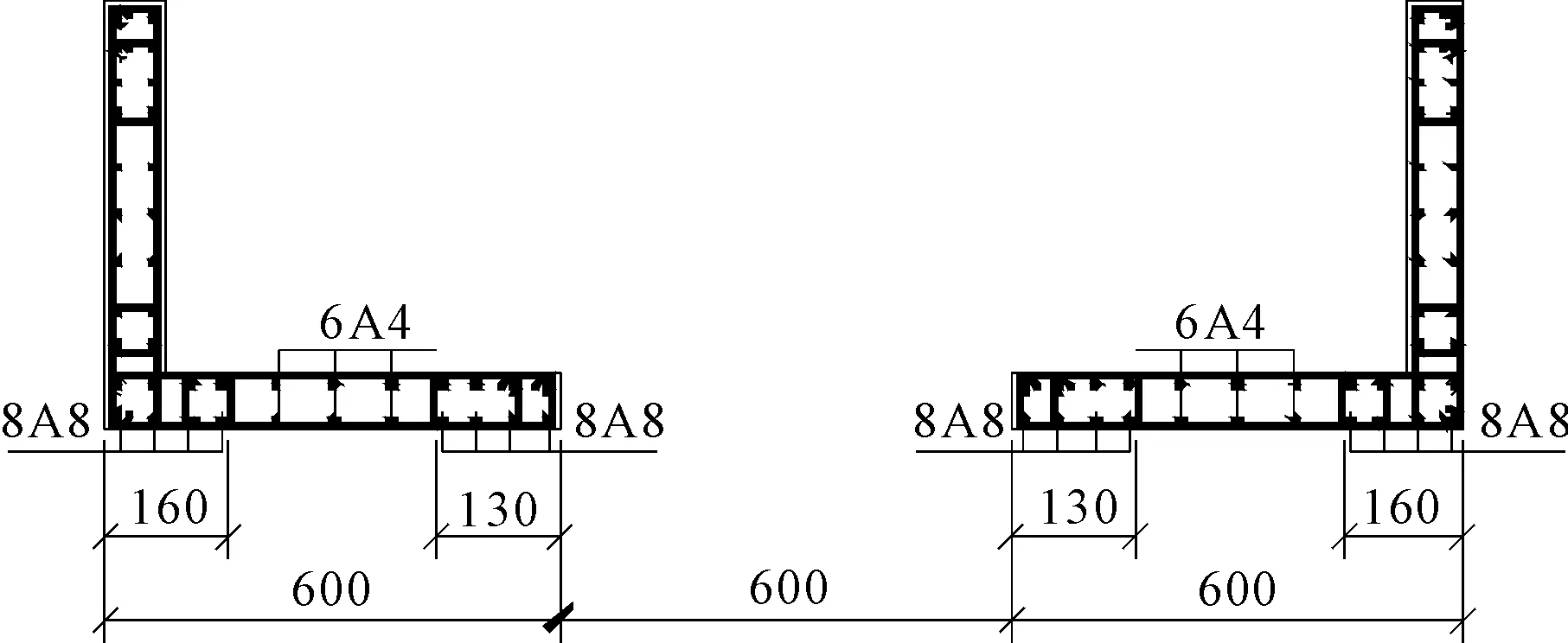
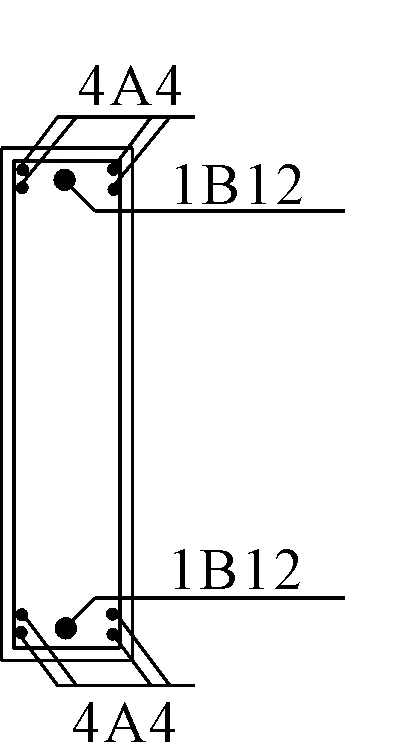
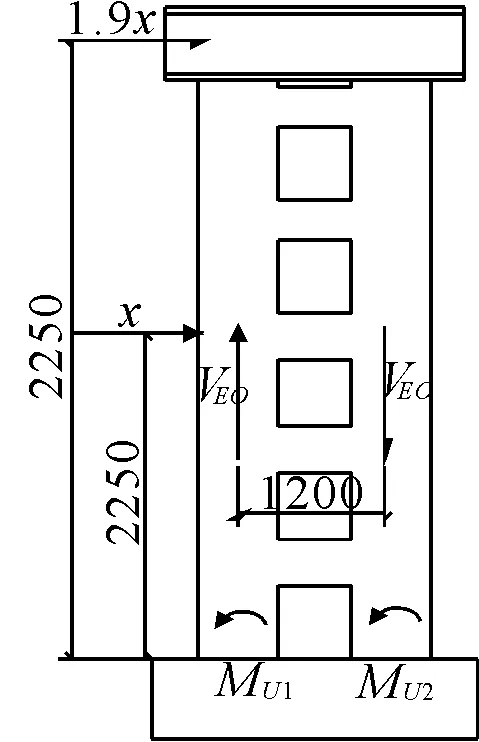
V=Mb/(0.5l)=86.4kN 满足强剪弱弯的要求。进行剪压比验算:V=86.4kN≤0.25βcfcbh0=202.9kN,满足要求。 对于第三个问题,本文采取增加剪力墙约束边缘构件纵筋配筋率及边缘约束构件长度的方式,使得剪力墙承载力满足力设计的要求。 通过基于能力设计原理对核心筒试件进行了相应设计,下面将对基于能力设计原理的核心筒受力性能进行验证,并与试验值进行对比分析,以验证基于能力设计方法的有效性和合理性。 2.1基本假定 (1)在水平地震荷载作用下,联肢剪力墙达到理想塑性极限状态,即连梁两端形成塑性铰,达到极限弯矩 ,剪力墙墙肢底部出现塑性铰,整体形成塑性铰机构; (2)剪力墙和连梁截面符合平截面假定; (3)连梁轴向变形忽略不计; (4)剪力墙墙肢处于弹性状态。 2.2材料强度 本文根据文献[13]试件破坏的实际情况,受拉钢筋选用试验实测的屈服强度平均值fym及极限强度平均值fum,取值见表1。考虑到混凝土强度对抗弯超强并没有太大影响,故忽略由于约束作用引起的混凝土强度超强,仍采用实测的轴心抗压强度平均值,即fcm=35.63 MPa。 表1 钢筋力学参数 2.3连梁极限承载力计算方法 连梁极限承载力的计算包括两方面内容,即连梁端部超强剪力和连梁整体极限抗弯超强的计算。其中连梁端部的超强剪力,会在相邻墙肢上产生轴向压力,这两个轴压力会组成一对力偶,来抵抗结构所承受的倾覆弯矩。弯曲或弯曲剪切破坏型连梁极限承载力的计算方法如下。 普通连梁两端的剪力超强,可以通过计算连梁端部的弯矩超强求得,在计算连梁端部弯矩时,应该考虑楼板有效受拉钢筋的作用。连梁极限承载力计算简图如图1所示,连梁整体抗弯极限承载力计算如下式: ML=fbmAs′(h-as-as′) (13) MR=fbm(As+As,slab)(h-as-as′) (14) 连梁两端极限抗剪承载力计算如下式: (15) 式中:VEO,i为连梁端部剪力超强;ML,MR分别为连梁两端的弯矩超强;As为连梁上部钢筋面积;As′为连梁下部部钢筋面积;As,slab为连梁上部楼板有效受拉区内钢筋面积;as和as′分别为连梁上部及楼板有效受拉区钢筋合力点至截面边缘的距离及连梁底部钢筋合力点至截面边缘的距离。 图1普通连梁极限承载力计算简图 2.4双肢剪力墙极限承载力的计算方法 对于双肢剪力墙,当其在地震荷载作用下,墙肢会承受由连梁端部传来的剪力超强VEO,i,其中一个墙肢受压,而另一侧墙肢则受拉。现以带翼缘L形单肢剪力墙组成的双肢墙为例(如图2),说明双肢剪力墙极限承载力的计算方法。 (1)左墙肢底部极限抗弯承载力计算 当腹板墙体轴力大于等于连梁施加的剪力时(N+N1≥VEO),其平衡方程为:N+N1-VEO+TS1+TS2+TSW=xbfcm+TS2′ (16) 极限抗弯承载力为: (17) 图2双肢剪力墙的受力状态 N+N1-VEO+TS1+TS2+TSW+TS2′=0 (18) 极限抗弯承载力为: (19) (2)右墙肢底部极限抗弯承载力计算 当极限受压区高度x≤hf′时(不考虑受压区暗柱钢筋的抗压强度),其平衡方程为: (20) 极限抗弯承载力为: (21) 当极限受压区高度x≥hf′时(考虑受压区暗柱钢筋的抗压强度),其平衡方程为:N+VEO+N2+TS2+TSW=hf′(hf′-b)fcm+xbfcm+TS2′ (22) 极限抗弯承载力为: (23) 2.5混凝土核心筒极限承载力计算 2.5.1构件材料强度确定 以试件文献[13]中试验试件CW-1为例进行分析计算,见图3。由试验过程及结果可知连梁角部钢筋屈服明显,其中部分连梁水平分布筋被拉断,而抗剪斜插筋也发生屈曲。墙肢根部没有出现明显压碎现象,但在受拉侧出现了水平抗拉通缝,通过对两片墙肢的暗柱纵筋应变分析,可知纵筋均已屈服,但并未达到其极限状态。因此材料超强强度取值见表1,腹板分布筋配筋率为ρw=0.0032。单片墙肢轴力为321.4 kN。 2.5.2连梁极限强度计算 对于普通连梁因大震作用引起的剪力超强,可由连梁两端的弯曲超强计算得到。首先计算连梁整体极限抗弯承载力,连梁截面示意图见图4。截面上达到极限抗拉强度的有4根φ4的冷拉钢丝,达到屈服强度的钢筋有2φ12。通过式(13)、式(14)可求得连梁整体抗弯承载力MR=ML=25.9 kN·m,再由式(15)求得连梁受剪承载力为VEO,i=86.4 kN 图3CW-1墙肢截面示意图 2.5.3核心筒极限承载力计算 核心筒试件墙肢截面配筋及尺寸如图3所示,左右两侧墙肢宽度均为600 mm。通过式(16)、式(17)可得到左墙肢整体抗弯承载力MU1=441.8 kN·m,通过式(20)、式(21)可得到右墙肢整体抗弯承载力MU2=309.6 kN·m 试验加载情况见图5,可列核心筒平衡方程: 2.25x+4.31×1.9x=2(MU1+MU2+1.2VEO) 计算可得核心筒水平极限承载力Vu=2.9x=708.2 kN 图4连梁截面配筋 图5核心筒计算模型 同理,对试件CW-2及CW-3进行计算,得到水平极限承载力,分别为750 kN和660 kN。对于CW-4连梁破坏由剪切控制,可考虑深连梁剪力由腹筋控制,从而进行相应计算,计算值为1 025.5 kN。 理论计算结果及其与试验结果的对比见表2。由表2中数据可知,理论计算值较试验值稍稍偏大,和试验值较为接近,最大误差仅为7.1%。表明在主轴方向,核心筒极限承载力可简化为带翼缘的双肢剪力墙计算理论进行分析,关于理想耗能机理的假设也和试验较好符合,在对材料强度合理取值下,计算结果较为准确。另外,由表2可知,连梁在筒体整体抗侧能力中起到很大的作用,连梁的抵抗弯矩占整个试件的40%以上,其中CW-4能达到56.43%,这主要是因为试件CW-4的连梁跨高比较小,连梁抗弯刚度较大,因此其极限抵抗弯矩也相应较大。 表2 核心筒试件极限承载力计算值与试验值比较 本文基于能力设计原理提出了核心筒合理的屈服机制和破坏模式,并通过能力设计思想对本文核心筒试件进行了相应设计验证。提出了核心筒理想塑性极限状态为首先在连梁端部形成稳定耗能的塑性铰,进而梁铰形成的大变形使剪力墙墙肢底部也形成塑性铰,整体形成机动体制,从而使核心筒受力极限状态符合“强墙肢弱连梁”设计思想。 介绍了以弯曲破坏形态为主连梁极限承载力的计算过程;基于能力设计原理,根据带翼缘L形单肢剪力墙极限承载力的计算方法,推导出了双肢剪力墙墙肢极限承载力的计算公式。并以核心筒试件CW-1为例,根据极限承载力计算方法得到核心筒水平极限承载力和抗倾覆弯矩,同时得到其余3个主轴方向的核心筒试件极限承载力计算值,并与试验值进行了比较,结果较为吻合,结果表明在主轴方向,核心筒极限承载力可简化为带翼缘的双肢剪力墙计算理论进行分析,关于理想屈服机制的假设也和试验较好符合,在对材料强度合理取值下,计算结果较为准确。计算结果还显示,连梁在筒体整体抗侧能力中起到很大的作用,连梁的抵抗弯矩占整个试件的40%以上。 参考文献: [2]何西伟,李青宁.T形短肢剪力墙的变形杆系广义墙元模型[J].水利与建筑工程学报,2008,6(4):5-7. [3]王建祥,苏枋,胡景龙,等.短肢剪力墙静力性能数值模拟试验研究[J].水利与建筑工程学报,2006,4(2):26-28,40. [4]张松,吕西林,章红梅.钢筋混凝土剪力墙配箍参数设计方法试验研究[J].结构工程师,2009,25(1):83-89. [5]龚治国,吕西林,姬守中.不同边缘构件约束剪力墙抗震性能试验研究[J].结构工程师,2006,22(1):56-61. [7]伍云天,代崇民,周忠亮,等.剪切机制耗能端板螺栓连接组合联肢剪力墙钢连梁抗震性能试验研究[J].建筑结构学报,2014,35(4):255-261. [8]童根树,苏健.联肢剪力墙的刚度、稳定性以及二阶效应[J].工程力学,2012,29(11):115-122. [9]张云鹏,曹万林,张建伟,等.内藏钢桁架深连梁联肢剪力墙抗震性能试验研究[J].世界地震工程,2010,26(2):19-24. [10]Paulay T,Priestley M J N. Seismic Design of Reinforced Concrete and Masonry Buildings[M]. New York:John Wiley &Sons,Inc,1992. [11]缪志伟.钢筋混凝土框架剪力墙结构基于能量抗震设计方法研究[D].北京:清华大学,2009. [12]黄东升.剪力墙结构的分析与设计[M].北京:中国水利水电出版社,2006. [13]史庆轩,侯炜,刘飞,等.钢筋混凝土核心筒抗震性能试验研究[J].建筑结构学报,2011,32(10):119-129. [14]黄小坤.剪力墙连梁纵向钢筋构造配筋率探讨[J].建筑结构,2004,34(1):43-45. [15]刘清山,梁兴文.抗震剪力墙小跨高比连梁受剪承载力的软化拉压杆模型解[J].建筑科学,2008,24(7):5-9. AnalysisonStructurePerformanceandUltimateBearingCapacityofReinforcedConcreteCoreWalls XUE Dong-zhi (ShaanxiConstructionEngineeringGroupCorporation,Xi’an,Shaanxi710003,China) Abstract:It is important for the seismic performance of the entire structure that the reinforced concrete core walls form good yield mechanism and failure mode under strong earthquakes. Based on the capacity design method,it was proven that the “strong shear wall-weak coupling beam” structure type performed reasonable yield mechanism by comparing various damage models. According to the calculation method of “L” shape shear wall with flange,the ultimate bearing capacity of double shear wall was deduced. By proposed calculation method,the ultimate bearing capacity and resistive overturning moment values of concrete core walls were calculated through an instance. The values drawn from that were in good agreement with the experimental results. The study result indicates that in principal axis direction,the calculation of the core walls can be simplified as that of double shear walls with flange. It also suggests that coupling beams play a major role in the lateral resistant system. The resisting moment of coupling beam is more than 40% of the total moment. Keywords:reinforced concrete core walls;mechanical performance;damage mode;capacity design method;ultimate bearing capacity DOI:10.3969/j.issn.1672-1144.2014.05.002 中图分类号:TU312+.1 文献标识码:A 文章编号:1672—1144(2014)05—0007—06 作者简介:薛东智(1961—),男,陕西三原人,高级工程师,主要从事工程结构建造与管理、加固改造等方面的工作。 基金项目:国家自然科学基金资助项目(51178380) 收稿日期:2014-06-30修稿日期:2014-07-30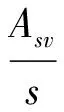
2 核心筒的极限承载力分析
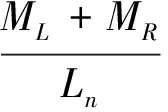
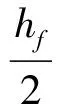
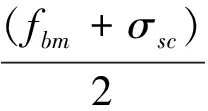
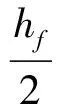


3 承载力结果对比及分析

4 结 语

