基于负约束条件下最大似然估计的无线传感网络定位算法*

丁海强,齐光快,庄华亮,何熊熊

(浙江工业大学信息工程学院,杭州 310023)



基于负约束条件下最大似然估计的无线传感网络定位算法*

丁海强,齐光快,庄华亮*,何熊熊

(浙江工业大学信息工程学院,杭州 310023)

针对基于RSSI(Received Signal Strength Indicator)的无线传感网络定位算法精度不高的问题,提出一种负约束条件下的似然估计定位算法。当未知节点在参考节点的通信范围之外时,引入负约束条件来提高定位精度。主要工作可分为三部分:第一,根据RSSI值测量参考节点与未知节点之间的距离。第二,根据参考节点与未知节点通信关系建立正约束和负约束条件下的似然估计函数。第三,利用粒子群优化算法找到未知节点的最佳位置。仿真结果表明,引入负约束条件可以提高定位精度,且优于传统的定位算法。

无线传感器网络;负约束;最大似然估计;定位;粒子群优化

20世纪90年代以来,人们就开始关注无线传感器网络WSN(Wireless Sensor Network)技术,被认为是21世纪最重要的技术之一。无线传感网络广泛应用于军事、环境、工业等方面[1]。在无线传感网络技术中,节点定位是无线传感网络的主要支撑技术。定位技术可应用于目标识别、目标跟踪、移动目标的检测、人员定位等[2]。因此,随着无线传感器网络技术的发展,如何获得准确的节点位置信息也变得越来越重要。

目前,典型的定位方法主要分为两类:无需测距和基于测距。无需测距方法不需要测量节点间的距离、角度或者其他信息,而是根据网络的连接度来实现定位,其缺点是定位精度低。此类方法主要为质心定位算法,DV-hop算法和APIT算法[3]。基于测距方法主要采用额外的硬件来测量节点间的距离来实现定位。虽然此类方法需要额外成本并且消耗能量,但能获得比较高的精度。此类方法主要为信号到达角度(AOA),信号到达时间(TOA),信号到达时间差(TDOA)和RSSI等[4-7]。在实际应用过程中(尤其是室内环境),大部分方法都采用节点间信号强度与距离之间的关系来实现测距[8]。

下面介绍几种典型的定位系统:

微软公司的RADAR系统是基于IEEE802.11标准的室内定位系统[9],它事先在测量区域内大量记录各个位置的RSSI值,定位时,根据当前的RSSI值来与之前标定好的RSSI进行匹配来确定节点位置(定位误差大约在6 m)。此系统要求定位前需大量测试各位置的RSSI值,因此工作量大,布置成本高。

麻省理工学院的Cricket室内定位系统主要由Beacon节点和Listener节点组成[10]。Beacon节点同时发射超声波和射频信号,Listener节点侦听到信号后,根据TDOA测距原理(测距范围大约在0～10 m)并用三边定位法对未知节点进行定位。此系统容易受障碍物影响,非常不适合非视距(NLOS)复杂的环境。

浙江大学的INEMO系统根据房间的布局把建筑物分成不同的等级[11]。当用户(已携带节点)靠近附近的房间时,传感器节点可以与之相近的参考节点交换信息,根据信号接收强度,判断用户所在位置。此系统只适用于办公楼比较规格的室内环境。另一方面,在定位时,因为信息通信量大,易造成能量消耗大,使得定位精度也不高。

针对上述各定位系统的不足,提出一种负约束条件下的似然估计定位算法。第1节中讨论了RSSI测距原理,给出了距离的对数正态分布模型。第2节中根据参考节点与未知节点之间的通信关系,建立正约束和负约束条件下的最大似然函数,并应用粒子群优化算法找到未知节点位置。第3节根据算法原理,用计算机仿真验证算法的可行性。最后,给出本文结论。

1 RSSI测距模型

RSSI常用于无线传感定位,它根据发送端和接收端之间的功率损耗来计算出它们之间距离。利用理论或者经验模型得到功率损耗与距离之间的关系为下式:

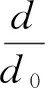
(1)

其中PL(d)为距离D=d时的接收信号强度,P为距离d时的接收信号强度,n为路径损耗指数,ξ为零均值标准差为σp的随机变量。在实际应用中,变量σp不会随距离的变化而变化,只与所处的环境有关。化简式(1)为:

P=P0-10nlgd-ξσp

(2)

其中P0为距离1 m时的接收信号强度。通过实际测试可知,参数n和ξσp是相互独立的,可以对测量数据进行最小二乘估计得到。因此,当两个节点间的RSSI值测量得到时,它们之间的距离就可以计算得到,即:

(3)

如图1所示,测量实验室内RSSI值与距离之间的关系。由图可知,随着节点间距离的增加,RSSI值呈递减趋势。试验中,采用TI公司的CC1110射频芯片作为传感器节点,变量ξσp和n可以通过对测量得到的RSSI值进行最小二乘估计得到。我们测试得到n=2.41,ξσp=-3.54。根据测试数据,可拟合得到对数正态阴影传播模型。

图1 距离与RSSI之间关系

根据式(2),距离d为对数正态分布,改写式(3)为:

lnd～N(μd,σd)

(4)

其中μd近似等于lnd,σd等于σp/10n。对于特定的物理环境,变量σd可估计得到且为常量。如图2所示,实际测试RSSI值d=10 m时的概率密度函数曲线。图中可以看出,曲线的最高点最为接近距离的真实值。因此,我们可以把概率密度函数的最大值的点作为对未知节点的定位。在实际环境中,一直存在遮挡效应,为了提高定位的精度,减少非视距误差,可以使用卡尔曼滤波方法减小测距误差[12-13]。下面介绍负约束条件下似然估计定位算法。

图2 RSSI=-64.5 dBm时距离d的对数正态分布

2 正负约束条件下的似然估计定位

2.1 正约束条件下似然估计

在实际应用中,未知节点在参考节点的通信范围内时,测得的RSSI值比较准确,从而计算得到相对精确地距离。如图3所示,待定位节点在参考节点的通信范围之内,我们称这种关系为正约束。

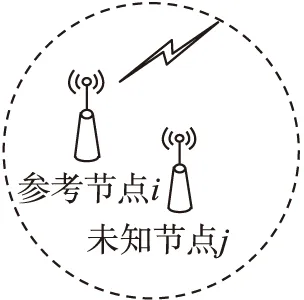
图3 参考节点与未知节点的正约束关系

假设传感器网络由i个参考节点和j个未知节点组成。未知节点的位置向量X可定义为:

X=[x1…xjy1…yj]T

(5)

则距离dij的对数正态分布为:

(6)

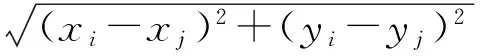
(7)

因此,可以得到距离dij的概率密度函数ρij(X)为:

(8)

设概率密度函数ρij(X)为似然函数,即得到正约束条件下的似然函数:

(9)

然而,当未知节点在参考节点的通信范围之外时,也可以利用它们之间的关系进行对未知节点的定位,下面介绍负约束条件下的似然估计定位。

2.2 负约束条件下似然估计

假如参考节点和未知节点之间没有通信链接(或者RSSI值小于RSSImin),则可以推测出它们之间的距离大于其通信范围。如图4所示,未知节点在参考节点的通信范围之外,我们称这种关系负约束。

图4 参考节点与未知节点的负约束关系

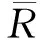
(10)

(11)

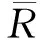
(12)

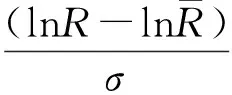
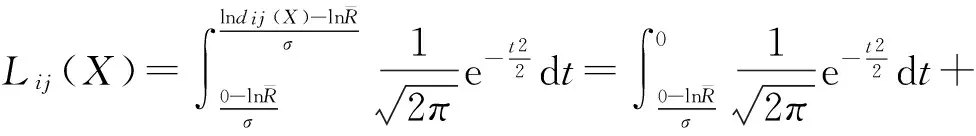
(13)

(14)

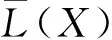
(15)

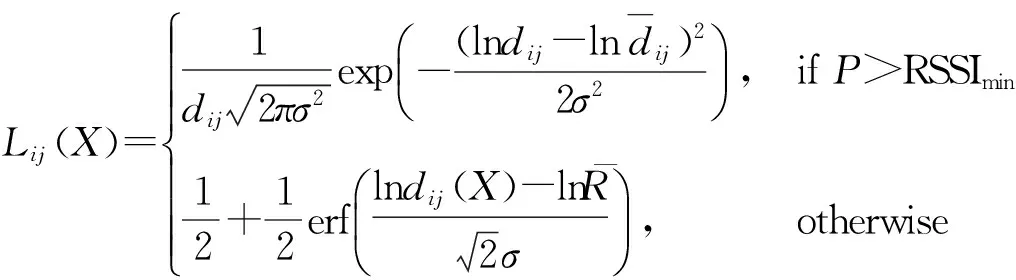
(16)

为了找到最大似然估计,将式(16)转化为最小二乘问题,即

(17)

(18)

下面介绍利用粒子群优化算法解决最小二乘问题。

2.3 粒子群优化定位

粒子群优化是近年来发展起来的一种新的进化算法,它模仿于生物鸟群的社会行为。粒子群优化算法具有收敛速度快、易实现的特点,是一种高效实用的搜索算法。在无线传感网络中,可使用PSO算法有效的解决定位问题[14-15]。

PSO算法首先初始化m个随机粒子(候选解称之为粒子),每个粒子有自己的位置且以一定的速度飞行。算法根据粒子本身和同伴的飞行经验动态地调整参数,通过迭代计算得到目标函数的最优解。假设n维搜索空间中粒子的位置和速度分别为X=[x1…xjy1…yj]T和V,在每一次迭代中,粒子通过追踪个体最优值pbest和群体最优值gbest来更新自己。找到这两个最优值时,粒子根据下式来更新自己的速度和位置。

VX(k+1)=wVX(k)+c1r1(k)(pbest(k)-X(k))+
c2r2(k)(gbest(k)-X(k))

(19)

X(k+1)=X(k)+VX(k+1)

(21)

其中c1和c2是学习因子,r1(k)和r2(k)是随机对角矩阵并且服从[0,1]均匀分布。pbest是迭代过程中的个体最优解,gbest是群体最优解。粒子群优化定位算法步骤为:

①根据RSSI测距模型的得到距离d,即式(3)。

②当未知节点在参考节点的通信范围之内时,引入正约束条件得到似然函数,即式(9)。

③当未知节点在参考节点的通信范围外时,引入负约束条件,联合正负约束条件得到似然函数,并转化为最小二乘问题,即式(17)、(18)。

⑤把每个粒子带入目标函数中,得到各粒子的优劣性,将当前各粒子的位置存储于pbest中。根据各粒子的优劣性把pbest中最优粒子存储于gbest中,再按照式(19)、式(20)更新粒子的位置和速度。

⑤重复步骤⑤,达到所设定的迭代次数或定位精度时,停止搜索,输出最优粒子gbest的位置,即定位结束。

3 仿真分析

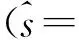
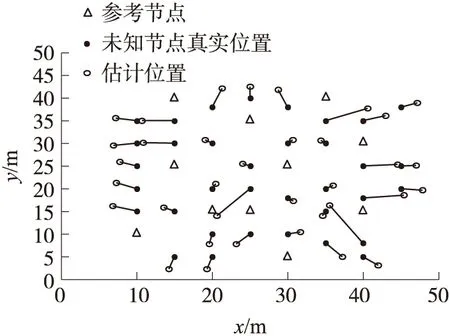
图5 正约束条件下的似然估计定位

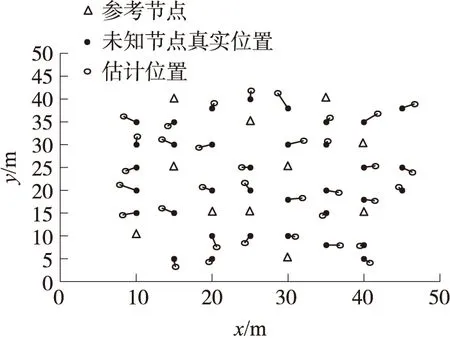
图6 正负约束条件下似然估计的定位

3.1 参考节点数量对定位的影响

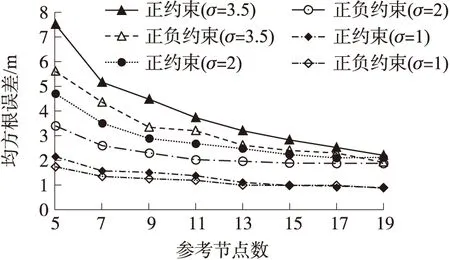
图7 参考节点数对定位误差影响

这里主要讨论参考节点数对定位误差的影响。计算仿真中,维持未知节点数量不变,持续增加参考节点的数量,如图7所示。仿真结果表明,随着参考节点数的增加,定位误差不断的减小,相比较于正约束条件下的似然估计定位,引入负约束条件可以提高定位精度。一般而言,增加参考节点数,必然增加网络密度,未知节点将收到更多的参考信息,必然提高定位精度。然而,当参考节点数达到一定数量时,定位误差趋向于某一定值,此时定位精度主要取决于测距误差。

3.2 测距误差对定位的影响

现实物理环境中,存在遮挡效应,必然在测距过程中产生误差。计算仿真中,讨论N1=7(N1为参考节点数)和N1=11两种情况下,比较测距误差对传统三边定位、正约束条件下似然估计、正负约束条件下似然估计定位影响。如图8所示,随着距离标准差σ的不断增大,定位误差也随着增大。图中可以看出,正负约束条件下的似然估计定位误差最小。如表1所示,相比较于正约束条件下的似然估计,引入负约束可以提高定位精度,大约为20%。相比较于传统的三边定位算法,联合正负约束条件下的似然估计定位算法误差可减小34.3%左右。

图8 测距误差对定位误差影响

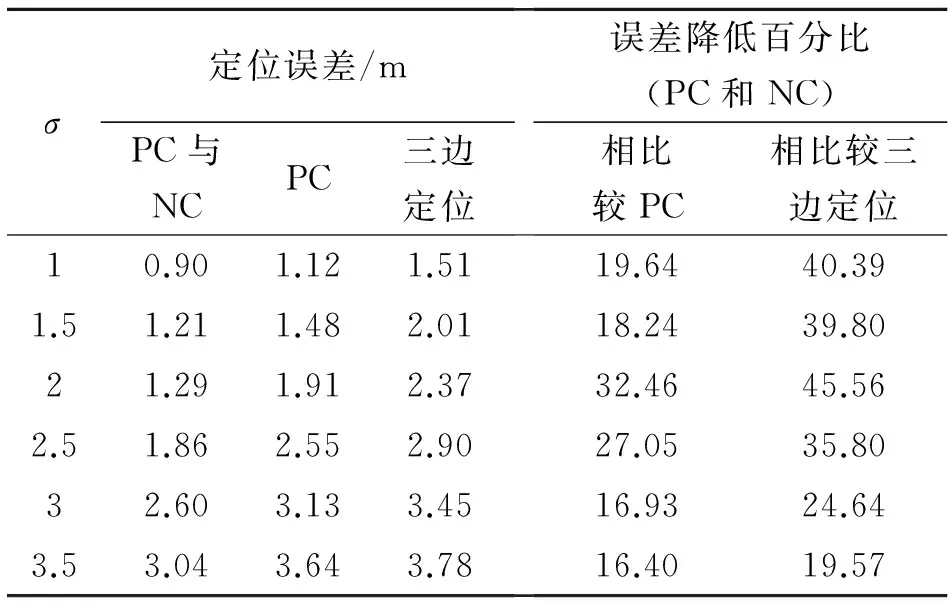
表1 参考节点N1=11时各定位算法的性能比较

注:PC为正约束,NC为负约束

3.3 算法迭代次数对定位误差影响

仿真实验中,布置11个参考节点来分析算法迭代次数对定位误差的影响。如图9所示,迭代160次时,定位误差开始收敛于某一常数,此时定位误差主要取决于测距误差。当然,随着迭代次数的增加,定位误差必然收敛于最小值,但此时必然增加算法的复杂度。因此,在误差能接受的范围内,需要合理的选择迭代次数。

4 结论

本文提出了一种负约束条件下的似然估计定位算法,该算法建立于RSSI测距基础上,联合正约束和负约束条件建立似然估计函数并利用粒子群优化算法找到未知节点的位置。仿真结果显示,引入负约束条件可提高定位精度,且比传统的定位算法在稳定性方面也更优。下一步工作中,将重点考虑在不同的物理环境中怎样合理的选择负约束条件,使得定位误差最小。

[1] Low K S,Win W N N,Er M J. Wireless Sensor Networks for Industrial Environments[C]//Computational Intelligence for Modelling,Control and Automation,2005 and International Conference on Intelligent Agents,Web Technologies and Internet Commerce,International Conference on.IEEE,2005,2:271-276.

[2]Arora A,Dutta P,Bapat S,et al. A Line in the Sand:a Wireless Sensor Network for Target Detection,Classification,and Tracking[J]. Computer Networks,2004,46(5):605-634.

[3]Niculescu D,Nath B. DV Based Positioning in Ad Hoc Networks[J]. Telecommunication Systems,2003,22(1-4):267-280.

[4]Niculescu D,Nath B. Ad Hoc Positioning System(APS)Using AOA[C]//INFOCOM 2003. Twenty-Second Annual Joint Conference of the IEEE Computer and Communications. IEEE Societies. IEEE,2003,3:1734-1743.

[5]程秀芝,朱达荣,张申,等. 基于RSSI差分校正的最小二乘——拟牛顿定位算法[J]. 传感技术学报,2014,27(1):123-127.

[6]陶为戈,朱昳华,贾子彦. 基于RSSI混合滤波和最小二乘参数估计的测距算法[J]. 传感技术学报,2012,25(12):1748-1753.

[7]Peng R,Sichitiu M L. Robust,Probabilistic,Constraint-Based Localization for Wireless Sensor Networks[C]//SECON. 2005:541-550.

[8]Xingbo W,Huanshui Z,Xiangyuan J. Collaborative Target Tracking in WSNs Based on Maximum Likelihood Estimation and Kalman Filter[C]//Control Conference(CCC),2011 30th Chinese. IEEE,2011:4946-4951.

[9]Bahl P,Padmanabhan V N. RADAR:An in-Building RF-Based User Location and Tracking System[C]//INFOCOM 2000. Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings. IEEE. Ieee,2000,2:775-784.

[10]Priyantha N B,Chakraborty A,Balakrishnan H. The Cricket Location-Support System[C]//Proceedings of the 6th Annual International Conference on Mobile Computing and Networking. ACM,2000:32-43.

[11]Hongbin L,Xingfa S,Jun Z,et al. Inemo:Distributed RF-Based Indoor Location Determination with Confidence Indicator[J]. Eurasip Journal on Advances in Signal Processing,2007,2008:1-11.

[12]Wann C D,Hsueh C S. Non-Line of Sight Error Mitigation in Ultra-Wideband Ranging Systems Using Biased Kalman Filtering[J]. Journal of Signal Processing Systems,2011,64(3):389-400.

[13]Chang X W,Champagne B. An Improved Extended Kalman Filter for Localization of a Mobile Node with NLOS Anchors[C]//ICWMC 2013,The Ninth International Conference on Wireless and Mobile Communications. Nice:IEEE,2013:25-30.

[14]Ren X,Gao C,Xi Y. A Node Localization Algorithm Based on Simple Particle Swarm Optimization in Wireless Sensor Networks[J]. Journal of Computational Information Systems,2013,9(22):9203-9210.

[15]Kulkarni R V,Venayagamoorthy G K. Particle Swarm Optimization in Wireless-Sensor Networks:A Brief Survey[J]. Systems,Man,and Cybernetics,Part C:Applications and Reviews,IEEE Transactions on,2011,41(2):262-267.

丁海强(1991-),男,硕士研究生,主要研究方向为无线传感器网络定位算法,dinghaiqiang666@163.com;

庄华亮(1967-),男,博士,讲师,从事智能系统、无线传感网络方面的研究,zhuanghl@zjut.edu.cn;

何熊熊(1965-),男,博士,教授,从事控制理论与应用、信号处理等方面的研究,hxx@zjut.edu.cn。

LocalizationinWSNBasedonMaximumLikelihoodEstimationwithNegativeConstraint*

DINGHaiqiang,QIGuangkuai,ZHUANGHualiang*,HEXiongxiong

(College of Information Engineering,Zhejiang University of Technology,Hangzhou 310023,China)

In order to improve the accuracy of localization in WSN(wireless sensor network)based on RSSI(Received Signal Strength Indicator),a maximum likelihood estimation approach with negative constraints to realize the localization of the unknown nodes is proposed. If there is no communication link between anchor node and unknown node,the negative constraints can be employed to improve the localization accuracy. The main work can be divided into three parts:firstly,the distance based on RSSI from the nodes is measured. Secondly,a series of positive and negative constrains are combined to build the modeling using the maximum likelihood estimation. Finally,particle swarm optimization is employed to find the optimal position. The simulation results show that the proposed approach outperforms some existing localization algorithm without negative constrains.

wireless sensor network;negative constrains;maximum likelihood estimation;localization;particle swarm optimization

项目来源:浙江省科技厅重大专项项目(C13011);浙江省科技厅公益技术研究项目(2013C33069)

2014-06-23修改日期:2014-09-12

10.3969/j.issn.1004-1699.2014.11.019

TP393

:A

:1004-1699(2014)11-1545-06