一种MEMS加速度计误差分析与校准方法

尹 杭,张 伟,袁琳峰

(电子科技大学电子科学技术研究院,成都 611731)



一种MEMS加速度计误差分析与校准方法

尹 杭,张 伟*,袁琳峰

(电子科技大学电子科学技术研究院,成都 611731)

MEMS传感器测量中一般存在确定性偏差和随机噪声两类误差,为提高其测量精度和稳定性,以MEMS加速度计为例,在建立其测量误差模型的基础上,提出一个综合的校准方案,同时对这两类误差进行补偿。其中使用Allan方差对随机噪声项进行量化分析,并综合采用了最小二乘法计算确定性校准系数,扩展卡尔曼滤波降低随机噪声等方法。通过实验验证,表明该方案可以有效校准加速度计测量的确定性偏差并降低随机噪声干扰,最终经过误差补偿后的测量数据在精度和稳定性方面都有明显提升。

MEMS传感器;误差校准;Allan方差;扩展卡尔曼滤波

随着智能手机等移动终端的快速发展,MEMS传感器的使用得以普及,从而大大降低了其成本,并且得益于MEMS传感器的体积小,功耗低,易于集成的特点,更促进人们将MEMS传感器用于汽车电子,智能移动终端,游戏控制器,机器人,GPS与IMU(Inertial Measurement Unit)组合导航[1]等各个方面。然而当前各种MEMS传感器受各种确定性偏差和随机噪声的影响较为明显,其测量精度和稳定性还不够高,使其应用受到限制,通过采取一定的技术对其校准,可以扩大其使用范围。在已有的校准方案中,一部分在精度需求不高的情况下,仅对确定性偏差进行了校准[2],例如对手机屏幕垂直或水平状态的检测。一部分仅从随机信号处理的角度对传感器数据进行频域或时域分析处理[3-6],未考虑确定性偏差或未根据状态空间模型给出完整的校准方案。

本文首先讨论了MEMS惯性测量传感器的误差来源,将其分为确定性偏差和随机噪声两类,并建立了一个综合了两类误差的测量模型。然后使用最小二乘法计算确定性校准系数,并通过计算Allan方差对随机噪声项进行量化分析,最后将确定性校准系数和随机噪声项的Allan方差作为参数用于所建立的扩展卡尔曼滤波器中,构成了一个完整的校准方案,同时包含了对确定性偏差和随机噪声的处理。

1 MEMS加速度误差模型与确定性校准系数的计算

MEMS加速度计误差来源[6-10]主要包括:

①常量偏差与校准误差,其中常量偏差指测量值到真实值的固定偏移,校准误差指加速度计在尺度因子、坐标系对齐性、测量轴交叉耦合、非线性上误差的总称。这些误差均为确定性误差,一般可以测量并校正。

②热机械白噪声,MEMS加速度计测量会受热机械噪声的干扰,表现为一系列同分布的零均值非相关白噪声随机变量,且有一个有限的方差。其对加速度计测量的影响表现为加速度积分中的速度随机游走。

③闪烁噪声,受电子模块或其他组件闪烁噪声的影响,MEMS加速度计偏差随时间漂移。通常使用偏置稳定性来描述传感器的偏差在固定条件下(包括恒定温度)和特定的一段时间内是如何漂移的。

④温度效应,环境温度变动和传感器自身的发热会导致偏差的变化,这种变化不包括在偏置稳定性测量中,因为后者是在固定条件下测量的。这一误差和温度间的关系是高度非线性的。

本文中实验在单一恒定的温度下进行的,不考虑温度效应。规定传感器测量平台所在空间坐标系为导航坐标系,用n表示,装配传感器的载体平台坐标系用p表示,传感器自身体坐标系用b表示。根据各误差项对测量影响程度的大小,并去除高阶小项,将加速度测量误差模型确定为[8]:

(1)

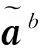
实验中加速度计固定于校准仪器上,规定导航坐标系的xyz轴正向依次指向北地东,重力在导航坐标系下表示为gn=(0,0,G)T,那么有an=-gn,其中G≈9.8 m/s2表示当地重力加速度的大小。φ和θ分别表示平台坐标系相对导航坐标系的滚动角(绕x轴旋转)和俯仰角(绕y轴旋转),ap表示平台坐标系下真实的加速度计比力测量,那么有:

(2)

现在仅考虑测量中的确定性偏差,在精度和计算复杂度间采取折衷,不计非线性误差影响。根据式(1)建立确定性误差校准模型为:

(3)

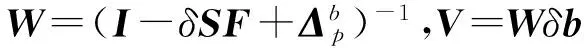
通过将加速度计固定于可以精确测量姿态角的平台上,采集不同φ和θ角下的测量数据,使用最小二乘法,根据(2)、(3)两式列线性方程组解得:

(4)

其中X为若干组不同φ和θ角对应的加速度计测量,Y为对应的根据式(2)得到的真实载体坐标系下加速度计比力测量。解得的校准系数矩阵W和偏差向量V将用于下一节卡尔曼滤波器的测量输出模型中。

2 使用Allan方差分析与扩展卡尔曼滤波降低随机噪声

Allan方差是一种描述时钟系统中噪声和稳定性的方法。其基本思想是取一个长的数据序列,并根据平均时间τ将数据切分为连续的n块,对第i块中数据取平均得到a(τ)i。然后取连续的两个块的平均值的差,平方后累加并除以一个缩放因子。最后对结果开方,便得到了特定平均时间平均值改变的量化结果。增加τ值,并重复上述过程,直到分割为9块为止,再往下,结果就开始失去意义[4-5]。Allan方差的定义为:

(5)

根据Allan方差和与噪声功率谱密度的关系,可以对各噪声项进行分析,仅考虑速度随机游走和偏置稳定性,Allan标准差和这两种随机噪声参数的关系以及对应的对数图斜率如表1所示[4-7]。

表1 Allan标准差与噪声参数及对数图斜率的关系

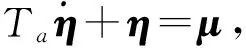
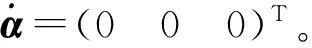
(6)

建立状态空间模型,其离散等效形式为[11-12]:

xk=Ak-1xk-1+Uk-1μk-1

(7)

zk=h(xk,νk)

(8)

采用扩展卡尔曼滤波方法的预测方程为:

(9)

(10)

更新方程为:

(11)

(12)

(13)

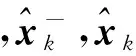
3 实验数据采集与处理

为确定确定性校准系数矩阵W和偏差向量V,采用图1所示的使用激光加工制作的具有较高水平和垂直精度的校准平台,由可以平稳放置并通过固定螺丝调整水平的三角平台、用于固定加速度计的正方体盒子以及高精度的水平仪组成。

图1 加速度计校准平台

通过将正方体盒子按不同面放置,收集加速度计在6个不同姿态上的各1万组数据,对应的滚动角φ和俯仰角θ如表2所示。

表2 加速度计6个不同姿态滚动角和俯仰角

然后根据式(4)便可计算得到确定性校准系数。

此外将加速度计固定于平台上保持不动,收集12 h的静态测量数据,根据式(5)计算加速度计各轴Allan方差,开方得到Allan标准差σ(τ)与平均时间τ的对数图如图2所示。

图2 加速度计Allan标准差

根据表1,从图2中,在斜率为-1/2的斜线上τ=1处读取加速度计各轴速度随机游走系数,取Allan标准差平直区间的最小读数为偏置稳定性系数,得到数据如表3所示。

表3 加速度计各轴速度随机游走与偏置稳定性

得到的确定性校准系数、随机游走系数、偏置稳定性系数作为参数用于上一节所建立的扩展卡尔曼滤波器,那么便可以对原始测量数据进行误差校准处理了。

4 实验结果与分析

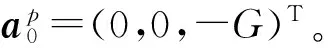
根据加速度计采样频率,趋向收敛的用时约为100 s,表明测量输出在较短时间内便达到稳定状态。截取最初200 s内经过误差补偿后的测量输出,如图4所示。

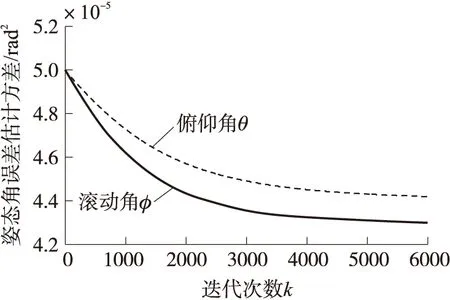
图3 姿态角方差收敛趋势

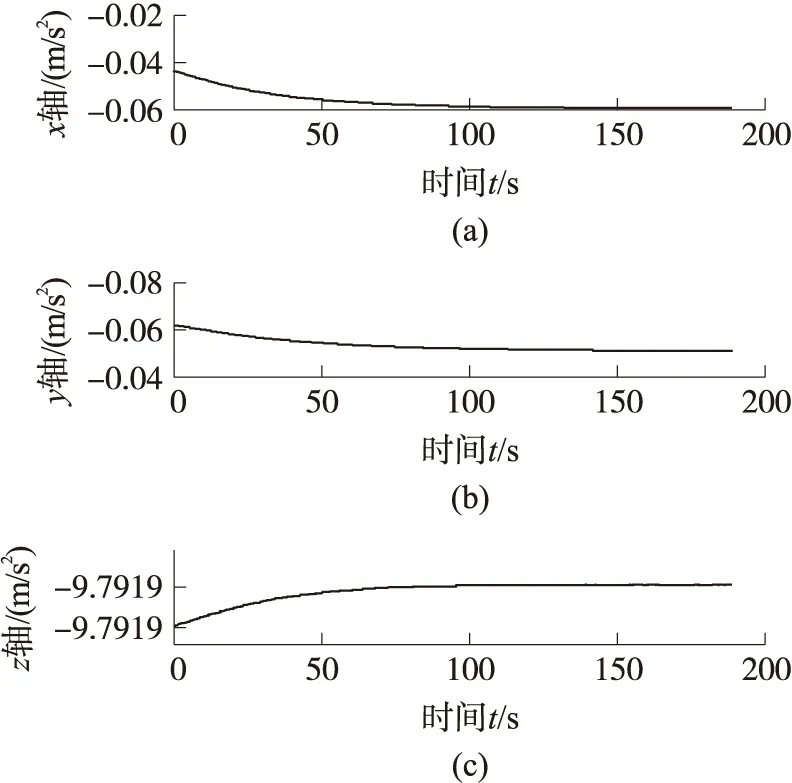
图4 加速度测量的误差补偿输出

与原始测量相比,经过误差补偿后的测量数据不受高频噪声干扰,且逐步趋向稳定。

表4 原始数据与误差补偿数据误差平方和

结果表明误差补偿后测量输出的误差平方和与原始测量输出相比有明显减小,其中z轴的减小更明显是由于加速度计测量不受偏航角的影响,因此只需考察x,y轴的输出,这表明经过误差补偿后的数据更接近真实值,具有更高的精度。

5 总结

本文针对MEMS加速度传感器测量中所存在的主要确定性偏差和随机误差提出一种综合性的校准方案,实验结果表明该方案可以有效提高MEMS加速度计的测量精度和稳定性。此外,对于其他类似的MEMS传感器,例如MEMS陀螺仪,电子罗盘,气压计等,只需进行相应的误差分析与建模,便可以将该方案进行扩展并加以应用。

[1] 赵鹤,王喆垚.基于UKF的MEMS传感器姿态测量系统[J].传感技术学报,2011,24(5):642-646.

[2]Mark Pedley.High Precision Calibration of a Three-Axis Accelerometer[EB/OL].http://cache.freescale.com/files/sensors/doc/app_note/AN4399.pdf,2013:1-39.

[3]宋海宾,杨平,徐立波.MEMS传感器随机误差分析及处理[J].传感技术学报,2013,26(12):1-5.

[4]Oliver J Woodman.An Introduction to Inertial Navigation[R].Cambridge:University of Cambridge Computer Laboratory,2007:1-37.

[5]Claudia C,Meruane Naranjo.Analysis and Modeling of MEMS Based Inertial Sensors[R].Stockholm:Signal Processing School of Electrical Engineering Kungliga Tekniska Hgskolan,2008:1-67.

[6]Vaibhav Saini,Rana S C,Kuber M M.Online Estimation of State Space Error Model for MEMS IMU[J].Journal of Modelling and Simulation of Systems,2010,1(4):219-225.

[7]Haiying Hou.Modeling Inertial Sensors Errors Using Allan Variance[D].Calgary:University of Calgary,2004:40-97.

[8]Jay A Farrel.高速传感器辅助导航[M].北京:电子工业出版社,2012:317-345.

[9]Petkov P,Slavov T,Stochastic Modeling of MEMS Inertial Sensors[J].Cybernetics and Information Technologies,2010,10(2):31-40.

[10]陈旭光,杨平,陈意.MEMS陀螺仪零位误差分析与处理[J].传感技术学报,2012,25(5):628-632.

[11]Welch G,Bishop G,An Introduction to the Kalman Filter[R].Chapel Hill:University of North Carolina at Chapel Hill,2006:1-16.

[12]Foxlin E.Inertial Head-Tracker Sensor Fusion by a Complementary Separate-Bias Kalman Filter[C]//Virtual Reality Annual International Symposium,1996,Proceedings of the IEEE 1996.IEEE,1996:185-194,267.

尹杭(1989-),男,湖北人,电子科技大学硕士研究生,研究方向为数字信号处理、基于惯性传感器的室内导航技术,yhvgo@126.com;

张伟(1974-),男,四川人,电子科技大学电子科学技术研究院博士研究员,硕士研究生导师,研究方向为数字信号处理、目标识别和数据融合,wzhang@uestc.edu.cn。

AnErrorAnalysisandCalibrationMethodofMEMSAccelerometer

YINHang,ZHANGWei*,YUANLinfeng

(Research Institute Electronic Science and Technology of UESTC,University of Electronic Science and Technology of China,Chengdu 611731,China)

MEMS sensors are usually susceptible to deterministic biases and stochastic noises,to improve their measurement accuracy and stability,take accelerometer sensor as an example,after a error model is built for it,an integrated calibration method to compensate both kinds of errors at the same time is proposed,in which Allan variance is used to analysis the random noise quantificationally.Besides,several kinds of methods including least square method to calculate deterministic calibration parameters,extended Kalman filter to decrease random noise are used.The experiment result shows that this method can efficiently calibrate the deterministic biases and decrease the influence of random noises,the error compensated measurement data has notable improvement in accuracy and stability.

MEMS sensor;error calibration;Allan variance;extended Kalman filter

2014-04-02修改日期:2014-05-30

10.3969/j.issn.1004-1699.2014.07.003

TP202

:A

:1004-1699(2014)07-0866-04