改进的距离重构三维定位算法*

张亚杰,段渭军*,王福豹,高 昂

(1.西北工业大学电子信息学院,西安 710072;2.物联网技术及应用国家地方联合工程实验室,西安 710072)



改进的距离重构三维定位算法*

张亚杰1,2,段渭军1,2*,王福豹1,2,高 昂1,2

(1.西北工业大学电子信息学院,西安 710072;2.物联网技术及应用国家地方联合工程实验室,西安 710072)

针对三维定位算法中节点坐标转换精度低的问题,在距离重构多维定位算法DR-MDS的基础上,提出了改进的距离重构三维定位算法。该算法在距离重构和MDS-MPA算法的思想下,采用优化的最小均方根偏差几何中心修正算法RMSD-GCC(Root Mean Square Deviation-Geometric Center Correction),先计算出坐标转换矩阵,然后利用锚节点的几何中心对所有节点进行修正,实现节点从相对坐标向绝对坐标较高精度的转换。算法可以实现有效的坐标转换,获得较好的定位效果。实验结果显示,与原多维定位算法相比,在不引入测距误差的情况下,改进算法在测距半径为15 m时定位精度提高14%,定位误差缩小至0.63 m,测距半径为35 m时,定位精度提高87%,定位误差几乎为0。该改进算法在三维空间中有更高的节点定位精度。

无线传感器网络;三维定位;坐标转换;几何中心修正

作为新一代的传感器网络,无线传感器网络WSNs(Wireless Sensor Networks)在军事国防、环境监测、智能家居、建筑物状态监控、城市交通、空间探索以及医疗健康监测等领域都有重要的科研价值和非常广泛的应用前景[1]。

无线传感器网络由大量微小型传感器节点组成,以无线通信的方式形成一个局部网络系统,实现目标物、目标区域的信息感知、数据采集以及对感知对象的信息处理,并发送给观察者。没有位置信息的数据采集是毫无意义可言的,节点的绝对位置信息在无线传感器网络的应用中至关重要。

当前,无线传感器网络节点定位的研究及实现都主要集中在二维平面的定位上[2],而在实际的节点部署中,节点通常被随机放置在三维空间中,二维空间定位已经无法满足当前的需求。而三维定位需要更加充分的位置信息,其网络大小、密度以及空间复杂度也随之增加,使得二维空间的定位算法无法直接在三维定位中使用[3-4]。实现高精度的无线传感器网络节点定位不仅必要,而且具有很重要的现实意义[5]。

1 相关工作

现在已经有很多关于三维空间定位的研究。全球定位系统GPS(Global Position System)是目前最为成熟、使用最广泛的定位系统,具有定位精度高、实时性好、抗干扰能力强等特点。但是无线传感器网络节点通常能源有限、体积较小、成本较低,GPS设备不适合在无线传感器网络中过多使用。

文献[3]提出一种基于LQI置信度的三维空间定位求精算法,依据大量的节点实验划分LQI置信度,并基于置信度修正RSSI值,减小测距误差对定位的影响。实验结果表明其算法较大程度提高了三维定位精度。

文献[4]通过信标节点发送广播信号的方法来进行测距,未知节点基于信号强度来获得与信标节点之间的距离,采用球域交叉位置的重心来估计未知节点的坐标。

文献[6]根据建筑物楼层高度固定的结构特点,提出一种分层结构的定位算法,相比于DV-Hop算法,定位精度有较大的提高。但该算法仅限于楼层明确的楼宇中。

文献[7]基于Euclidean定位算法,将信标节点与未知节点之间的距离抽象为六面体定点之间的距离,并利用坐标法进行求解。

文献[8]提出一种基于球面坐标的动态定位机制,将定位问题抽象为多元线性方程组求解问题,最终利用克莱姆法则获得未知节点的坐标。同时引入最小二乘法减小节点移动以及广播周期等过程中的误差。由于计算开销较大,节点无法长时间保持工作状态。

综上所述,目前无线传感器网络节点的三维定位算法还难以高效的实现较高精度的定位,这主要是由节点间距离和坐标转换精度不高引起的。针对距离重构的多维定位算法[9]在三维定位中坐标转换精度存在的问题,本文在距离重构的基础上,通过MDS-MAP算法得到节点间的相对坐标位置,同时采用更加精确的坐标转换方法来优化原有算法中的坐标变换过程,实现较高精度的三维坐标转换。仿真实验表明,改进算法在三维定位精度上有较大的提高。

2 算法描述及其改进

基于距离重构的多维定标算法利用节点之间的距离信息,进行距离重构,得到较精确地距离矩阵,然后使用MDS-MAP算法进行相对坐标计算,得到各节点之间的相对位置,最后使用最小均方根偏差几何中心算法得到三维空间中的绝对坐标。

2.1 线性距离重构及坐标计算

假设传感器网络中有5个节点,分别为1,2,3,i,j,其中除节点i,j之间的距离dij未知外,其他任意两个节点之间的距离均已知,这5个节点构成的平方距离矩阵为:

(1)

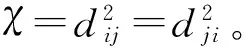
在获得节点对的距离信息后,通过距离重构的方法可以得到其他未知节点之间较精确的距离信息,未能成功重构的距离项仍采用最短路径替代。然后采用MDS-MAP算法进行坐标计算就可以得到网络中节点的位置坐标。根据各个节点之间的坐标构成一组相对坐标矩阵XR。

2.2 MDS-MAP算法三维坐标转换方法

通过计算得到节点的相对坐标以及锚节点的绝对坐标,经过平移、翻转和旋转等一系列的线性变换,将相对坐标转换到锚节点所在的坐标系中。

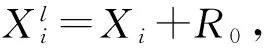
(2)

(3)

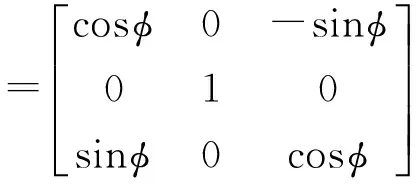
(4)

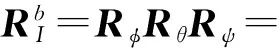
(5)

这样,在已知4个锚节点及其对应的相对坐标的情况下,可得

(6)

保留式(6)中非零项,得

(7)

即可求得转换矩阵中的对应各项得值。将除去锚节点外的其余m-4个传感器节点用相同的方法进行转换,有

(8)

这样,便得到所有节点的绝对坐标。

2.3 改进的坐标转换方法

采用MDS-MAP算法将相对坐标向绝对坐标的转换过程,其转换矩阵仅由4个锚节点进行确定,并不能较精确地实现相对坐标到绝对坐标之间的转换,增大了节点绝对位置的定位的误差。本文提出了RMSD-GCC算法,来实现较高精度的三维定位。

设锚节点坐标矩阵为Y,其对应的相对坐标矩阵为X,则定义:

(9)

其中,Q是旋转矩阵,QQT=I。当RMSD(X,Y)的值取到最小值,转换矩阵的转换精度最优。

令C=XTY,对C进行奇异值分解有

C=U∑VT

(10)

Q=UVT

(11)

不难验证Q=UVT为上述最小值问题的最优解[12]。

XA=XRQ

(12)

XA即为相对坐标旋转后得到的估计坐标位置。此时,分别计算锚节点的实际位置矩阵Y的几何中心以及经过旋转矩阵得到的估计位置矩阵X′的几何中心:

(13)

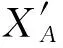
(14)

这样,锚节点的真实坐标和估计坐标就有相同的几何中心[13]。

2.4 算法实现过程

算法的实现过程可分为相对坐标计算过程和坐标转换过程。相对坐标计算过程中,距离矩阵经过距离重构并使用MDS-MAP算法计算出节点相对坐标位置。坐标转换过程中,相对坐标矩阵利用最小均方偏差和几何中心修正得到节点绝对坐标。

算法的伪代码实现如下:

1.Begin

2.Setdijbe the distance of nodei,j.

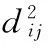
4.Search the numberkof unknown terms included inDN.

5.IFdijis unknown,

Select three public nodes ofi,j,using the formula(1)to calculatedij.

k=k-1

ENDIF

6.IFk>0,

goto 3.

ENDIF

7.XRis calculated as MDS-MAP algorithm.

8.SetY,X,X′ separately be the anchor node coordinate matrix,corresponding relative coordinate matrix and converted relative coordinate matrix.

9.Qis calculated as Equation(9),(10),(11).

10.XAis calculated as Equation(12).

11.Setyc,xcseparately be the geometric center of the anchor nodes and converted relative coordinate matrix.

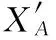
13.End

3 算法仿真分析及相关定义

3.1 相关定义

定义1设在三维空间中采用的定位误差计算为:

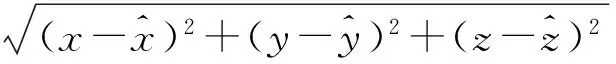
(15)

定义2设N为空间内部署节点数目,err为平均定位误差,则

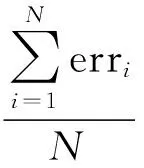
(16)

图1 节点定位效果图

3.2 算法仿真测试

本文主要通过改变节点的数量、测距半径、测距误差以及锚节点密度这4个参数,观察分析它们在仿真中分别对定位精度的影响,使得在硬件平台上使用时避免系统误差的产生。

为了验证算法的性能,本文使用MATLAB软件对该算法进行仿真实验。为了与现实空间大小相似,三维仿真环境设置为长宽均为30 m,高为10 m的立方体空间,在该区域内随机部署40个节点,每个节点的测距半径为15 m。实验中将已知节点均匀分布在网络区域内,并保证其分布的随机性。定位效果如图1所示。图中红色圆圈表示随机产生的节点的真实坐标,蓝色“×”号表示定位算法计算得到的坐标。从图中可以看出该定位算法计算得到的节点坐标与节点真实坐标基本重合,定位误差较小。

3.3 算法性能分析

3.3.1 测距半径和节点数量对定位精度的影响

设置测距半径分别为15 m、20 m、25 m、30 m和35 m,节点数量分别为30个、40个、50个、60个,通过改变测距半径,观察不同节点数量对应的节点定位误差。

从图2中可以看出随着测距半径的增加,定位误差逐步减小。当测距半径为25m时,节点之间的定位误差缩小至0.3 m以下。当测距半径超过30 m时,测距误差几乎为0。这是由于测距半径增大时,测距误差减小,定位精度提高。在测距半径相同的情况下,节点数量越多,定位误差越小。这是因为在替代不可测的距离在距离重构时,有更多可以选择的路径进行替代,更容易得到精确地距离,从而降低定位误差。

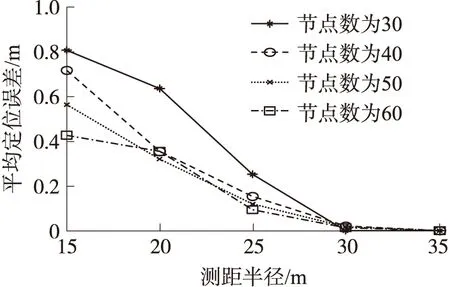
图2 测距半径和节点数量对定位误差的影响

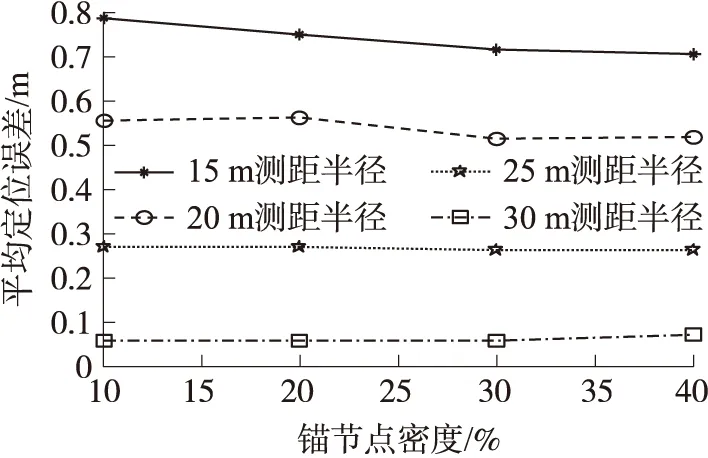
图3 锚节点密度对定位误差的影响

3.3.2 锚节点密度对定位精度的影响

设置总节点数量为40个,通过增加锚节点的密度,观察节点在测距半径分别为15 m、20 m、25 m、30 m时的定位精度,得到的图形数据如图3所示。在测距半径较小的情况下,节点的定位误差受锚节点密度变化影响较大,锚节点数量越多,定位误差越小;在测距半径较大的情况下,锚节点密度对定位误差的影响变小。这主要是因为测距半径较小时,节点间的测距值误差较大,导致定位后节点的几何中心和真实节点的几何中心之间的偏差比较大,增加锚节点的数量可以更好的修正节点的几何中心;在测距半径较大时,各节点之间的距离值更加准确,定位几何中心与真实几何中心偏差缩小,增加锚节点的数量对几何中心修正效果不明显。

3.3.3 DR-MDS算法与改进算法的平均定位误差的比较

设置节点的数目为40个,节点的测距半径为15 m,控制节点的原始位置不变,只对误差参数进行改变。乘性正态误差服从均值为0,方差为er2;均匀误差服从[-er2,er2]的均匀分布。经过100次实验后,取平均值作为仿真的结果。

图4(a)反映的是原算法与改进算法的节点在测量本节点与邻居节点之间的距离时,是否引入误差,引入哪种类型的误差对定位精度的影响的比较。其中,er2在乘性正态误差中表示方差值,在乘性均匀误差中表示最大偏差距离值。从图中可以看出,在3种情况下,随着误差参数的增加,两种算法的定位误差都逐步增加,由于正态误差的随机性,引入的误差更大。这表明节点间的测距精度对算法有一定的影响,当测距精度越高,定位误差越小。同时,在引入同类型误差的情况下,改进算法比原算法有更高的定位精度。

图4 改进算法与DR-MDS算法的比较

在不引入测量距离误差,锚节点和总节点的个数分别为4个和40个的情况下,原算法和改进算法都有较好的定位性能,对两种算法进行定位算法性能的比较。

从图4(b)中可以看出,节点的测距半径从15 m到35 m,随着节点测距半径的增加,两种算法的定位误差也逐步减小。在测距半径分别为15 m、20 m、25 m、30 m和35 m时,定位精度分别提高了14%、19.6%、28%、78%和87%。这主要是由于测距半径增加,节点之间的距离值更加准确,定位精度整体得到提高。同时,改进算法对几何中心进行修正,使得其平均定位误差更小。从数据中可以出,改进算法的定位精度至少提高了14%,定位误差缩小至0.7 m以内。

4 结束语

本文分析了多维空间定位中的距离重构算法,在距离重构和MDS-MAP算法的基础上,通过最小均方根偏差几何中心修正算法进行节点定位及其几何中心修正,对节点实现三维空间上坐标的较高精度转换。仿真结果表明,在不考虑测距误差的情况下,该改进算法在节点随机分布、测距半径较小时,定位精度可以提高14%,定位误差缩小至0.63 m,在测距半径较大时,定位精度可以提高87%,定位误差几乎为0,可以实现较高精度的三维空间定位。下一步我们希望使用该算法在硬件节点上进行实际测试,进一步验证算法的有效性和可靠性。

[1] 向满天,罗嗣力,戴美思. 无线传感器网络中一种改进的凸规划定位算法[J]. 传感技术学报,2014(8):1138-1142.

[2]刘健,沈海斌. 无线传感器网络的三维定位算法研究[J]. 传感器与微系统,2013(9):66-68,71.

[3]舒坚,刘琳岚,陈宇斌,等. 3D-RABLC:一种基于LQI置信度的三维空间定位求精算法[J]. 通信学报,2012,33(7):125-134.

[4]Gang H,Xinjiang X,Yehua W. A Three-Dimensional Positioning Algorithm for Wireless Sensor Networks Based on the Ball Field Intersection[C]//Electronics,Communications and Control(ICECC),2011 International Conference on. IEEE,2011:101-104.

[5]李彬,王文杰,殷勤业,等. 一种利用天线旋转的无线传感器网络定位算法[J]. 西安交通大学学报,2011(4):60-66.

[6]毛科技,戴光麟,夏明,等. 采用分层结构的WSN室内三位定位算法的研究和设计[J]. 小型微型计算机系统,2013,34(2):277-280.

[7]唐良瑞,宫月,罗艺婷,等. 一种基于Euclidean的无线传感器网络三维定位算法[J]. 电子学报,2012,40(4):821-825.

[8]戴桂兰,赵冲冲,邱岩. 一种基于球面坐标的无线传感器网络三维定位机制[J]. 电子学报,2008,36(7):1297-1303.

[9]黄亮,王福豹,段渭军,等. 基于距离重构的无线传感器网络多维定标定位算法[J]. 传感技术学报,2013,26(9):1284-1287.

[10]Regalia P A,Wang J. On Distance Reconstruction for Sensor Network Localization[C]//Acoustics Speech and Signal Processing(ICASSP),2010 IEEE International Conference on. IEEE,2010:2866-2869.

[11]Arfken G,Weber H J. Mathematical Methods for Physicists Academic[J]. New York,1985,19852:309.

[12]Golub G H,Van Loan C F. Matrix Computations[M]. Johns Hopkins University Press,1989.

[13]Wu D,Wu Z. An Updated Geometric Build-up Algorithm for Solving the Molecular Distance Geometry Problems with Sparse Distance Data[J]. Journal of Global Optimization,2007,37(4):661-673.

张亚杰(1990-),男,山西运城人,硕士研究生,主要研究方向为无线通信及分布式组网通信技术,1040464779@qq.com;

段渭军(1962-),男,陕西渭南人,研究员,硕士生导师,主要研究方向为无线传感器、网络信号处理,duanwj@nwpu.edu.cn;

王福豹(1963-),男,山西运城人,教授,博士生导师,主要研究方向为计算机网络、无线通信网络,wangfubao@nwpu.edu.cn。

AnImprovedDistanceReconstructingThree-DimensionalLocalizationAlgorithm*

ZHANGYajie1,2,DUANWeijun1,2*,WANGFubao1,2,GAOAng1,2

(1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710072,China;2.State and Local Joint Engineering Laboratory of IoT Technology and Application,Xi’an 710072,China)

In order to solve the problem of localization algorithm that node transformation accuracy from relative coordinate to absolute coordinate is low in three-dimensional,we proposed a improved distance reconstruct three-dimensional localization algorithm based on the distance reconstruct multi-dimensional localization algorithm. The algorithm based on the distance reconstruct and MDS-MAP algorithm adopted optimized Root Mean Square Deviation-Geometric Center Correction(RMSD-GCC)algorithm,first calculate the coordinate transformation matrix,then use the geometric center of the anchor node correct all nodes position,and realized node transformation from relative coordinate to absolute coordinate. The proposed algorithm can effectively transform coordinate,and get better location performance. Compared with old algorithm,the result shows that positioning accuracy in advanced algorithm increased by 14% and location error reduced to 0.8 m in distance radius equal to 15 m,positioning accuracy increased by 87% and location error almost reduced to 0 in distance radius equal to 35m under the condition of not introduce ranging error. The improved algorithm in three-dimension space has higher node localization accuracy.

wireless sensor networks(WSNs);three-dimensional localization;coordinate transformation;geometric center correction

项目来源:中央高校基本科研业务费专项资金项目(3102014KYJD033;3102014KYJD034)

2014-08-26修改日期:2014-10-19

TP393

:A

:1004-1699(2014)12-1681-06

10.3969/j.issn.1004-1699.2014.12.018