基于集总热容法的薄膜热电偶动态特性研究*

王晓娜,于方舟,杨遂军,祁漫宇,叶树亮

(中国计量学院工业与商贸计量技术研究所,杭州 310018)



基于集总热容法的薄膜热电偶动态特性研究*

王晓娜,于方舟,杨遂军,祁漫宇,叶树亮*

(中国计量学院工业与商贸计量技术研究所,杭州 310018)

为了分析不同边界传热条件下薄膜热电偶的动态特性,对薄膜热电偶瞬态测温过程建立零维传热模型。运用集总热容法分析对流换热、辐射换热两种边界条件下薄膜热电偶传热过程,通过建立热结点表面能量平衡关系得到传感器动态特性理论参数。采用水浴阶跃法、激光脉冲法对CO1-K型薄膜热电偶进行动态标定实验,通过对动态响应曲线进行Z-t变换得到薄膜热电偶动态特性实验参数。实验结果表明,集总热容法能够正确分析薄膜热电偶的动态特性,且计算不同边界条件下薄膜热电偶时间常数过程简单,时间常数理论值接近实验值。

薄膜热电偶;动态特性;零维非稳态传热模型;集总热容法;动态标定

动态特性是反映薄膜热电偶快速测温能力的重要性质,通常采用水浴法、激波法、电加热回路法、激光脉冲法等动态标定实验方法来确定动态特性参数[1]。由于薄膜热电偶缺乏统一的动态标定方案,不同标定方案边界传热条件不同,实验得出的动态特性参数存在差别。如何对不同边界条件下薄膜热电偶的动态特性进行理论分析是快速测温领域亟需解决的问题。

目前主要采用一维非稳态传热模型对薄膜热电偶进行动态特性分析,大连理工大学崔云先等人对热结点膜层内建立一维非稳态传热模型,推导得出热结点膜厚与动态特性之间的关系[2];上海理工大学杨丽红等人提出了基于对流换热为边界条件的一维非稳态薄膜热电偶传热模型,并计算出水浴阶跃条件下Cu/CuNi薄膜热电偶的时间常数[3]。采用一维非稳态传热模型分析动态特性结果较为准确,能够得出薄膜厚度对动态特性的影响,但是计算过程复杂,且没有对不同边界传热条件下热电偶动态特性进行分析。

本文以通用薄膜热电偶为对象,通过建立零维传热模型,结合集总热容计算方法,研究不同边界条件对薄膜热电偶动态特性的影响。分析表明不同边界条件下传感器动态特性不同,通过动态标定实验证明,采用集总热容法能够正确分析膜热电偶动态特性。

1 薄膜热电偶动态标定过程

薄膜热电偶电极膜厚通常为微纳米量级,热结点热容量小,可快速响应瞬态温度变化[4-6]。通常将热电偶看作一阶系统传感器,采用时间常数作为传感器动态特性参数,时间常数越小,热电偶动态特性越好。通常采用动态标定实验确定薄膜热电偶时间常数[7-8]。

动态标定实验中,薄膜热电偶需要具有理想阶跃前沿的激励信号,传统热电偶动态标定激励信号主要为阶跃信号,一般采用水浴、油浴、风洞作为阶跃信号激励源。随着对薄膜热电偶动态标定研究的深入,脉冲信号越来越多的作为传感器动态标定的激励信号,一般采用激光、激波、子弹作为脉冲信号激励源。薄膜热电偶对阶跃信号和脉冲信号的响应曲线如图1所示[9]。

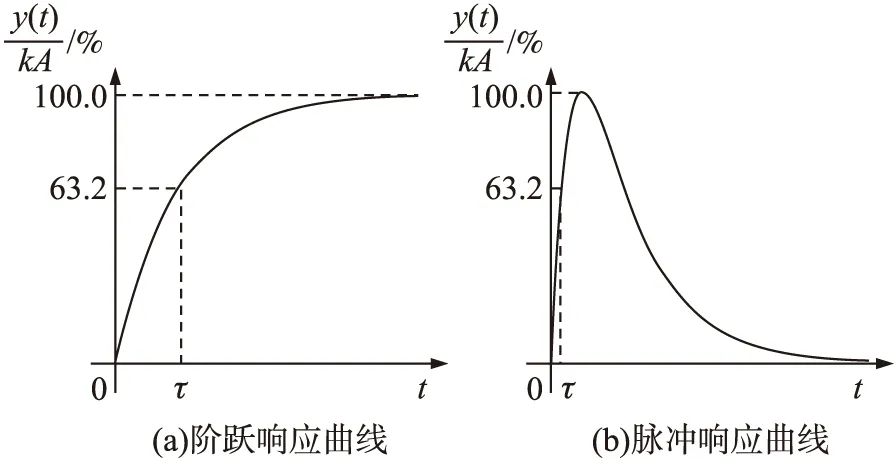
图1 一阶系统响应曲线

通常认为一阶传感器在阶跃前沿信号作用下,输出值达到最大值63.2%所经历的时间为时间常数τ[10],直接从图1所示响应曲线上读取时间常数的方法并没有涉及动态响应的全过程,测量结果仅取决于个别值,因此获取的时间常数可靠性较差。本文通过对一阶系统响应曲线进行Z-t变换来确定时间常数,并根据Z-t曲线与理想直线的拟合程度判断薄膜热电偶与一阶线性传感器的符合程度[11]。

图2 Z-t拟合曲线

热电偶对阶跃前沿响应曲线可以近似为一阶系统阶跃响应函数。

y(t)=A(1-e-t/τ)

(1)

令Z=ln[A-y(t)],将上升曲线转化为Z-t曲线,如图2所示。

由图2可得Z-t拟合曲线关系式为:

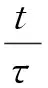
(2)

Z和时间t呈线性关系,通过Z-t线性拟合曲线的斜率和响应曲线上升幅值即可计算时间常数,时间常数为:

(3)

该方法考虑了响应的全过程,计算时间常数较为准确。

2 薄膜热电偶动态特性分析

由于薄膜热电偶没有统一的动态标定实验方法,因此实验得出的时间常数与实验条件密切相关,为了能够得到正确的时间常数,需要对不同边界条件下薄膜热电偶进行动态特性分析。除电加热回路法外,薄膜热电偶动态标定方法中边界条件主要为对流换热及辐射换热。本文采用水浴阶跃法、激光脉冲法两种动态标定方法提供两种边界条件,首先判断能否应用集总热容法分析薄膜热电偶动态特性,然后对薄膜热电偶瞬态测温过程建立零维传热模型,运用集总热容法推导出时间常数公式,最后计算出薄膜热电偶在两种边界条件下时间常数理论值[12]。

2.1 集总热容法

薄膜热电偶热结点体积小,热扩散系数大,表面换热速率相对内部导热速率非常小,内部温度扯平的能力远大于温度源与热结点表面换热的能力。在动态标定任何时刻,认为热结点的温度在空间上是均匀的,对热结点建立温度只随时间变化而不随空间坐标变化零维传热模型,通过建立热结点表面能量平衡关系来确定薄膜热电偶动态特性,这种忽略物体内部导热热阻的简化方法称为集总参数法。

集总热容法的应用条件为:

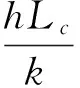
(4)

式中,Bi为毕渥数,h为对流换热系数,k为热电偶热结点导热系数,Lc为薄膜热电偶膜厚。毕渥数Bi为无量纲数,如果Bi≪1,说明热结点导热热阻远小于穿过流体边界层的对流热阻,此时可认为瞬态测温过程中任何时刻热结点中的温度分布是均匀的。

采用水浴阶跃提供对流换热边界条件,h=50～15 000 W/(m2·k),薄膜热电偶k=20 W/(m·k),Lc=15.8 μm,所以:

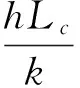
采用激光脉冲提供辐射换热边界条件,激光脉冲在热结点表面作用结束后,热结点暴露在空气中,此时热结点在空气中对流换热系数为h=5～100 W/(m2·k)。

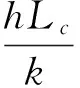
通过以上分析可知,薄膜热电偶在水浴和空气中满足集总热容条件,毕渥数远小于0.1,因此可以采用集总热容法对其动态特性进行分析。

2.2 两种边界条件下动态特性分析

2.2.1 对流换热边界条件下动态特性分析

将薄膜热电偶迅速置于温度为T∞的水浴中,此时传热过程如图3所示,热量以对流换热的方式从水中传输到热结点表面。根据集总热容法可以知,此时热结点随时间变化而升温。

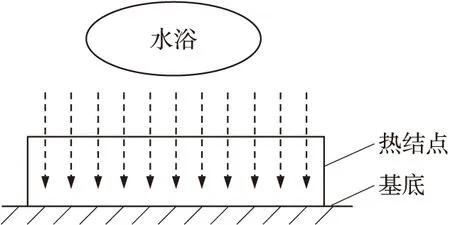
图3 水浴传热分析

在热结点表面建立热结点表面能量平衡公式

(5)

式中,h为水浴在热结点表面的对流换热系数,ρ、c、V、A分别为热结点密度、比热容、体积和表面积。

引入过余温度θ=T-T∞,T为热结点温度,T∞为水浴温度,由于T∞为常数则有dθ/dt=dT/dt,可得:

(6)

分离变量并从初始条件t=0、T(0)=Ti开始积分,Ti为热结点初始温度,θi为初始过余温度,可得:

(7)

计算积分式可得

(8)

该式用来确定热结点在流体中达到某个温度Ti所需的时间t。根据一阶系统时间常数的定义,当θi/θ=36.8%时,对流换热边界条件下时间常数为:

(9)

2.2.2 辐射换热边界条件下动态特性分析

对薄膜热电偶进行激光激励时,传热过程如图4所示,激光在脉冲时间tw内作用在热结点表面,激光入射深度内热结点的自由电子被激发,这种激发在10-13s内转化为热能,该能量在激光作用期间被厚度为l1的膜层吸收。

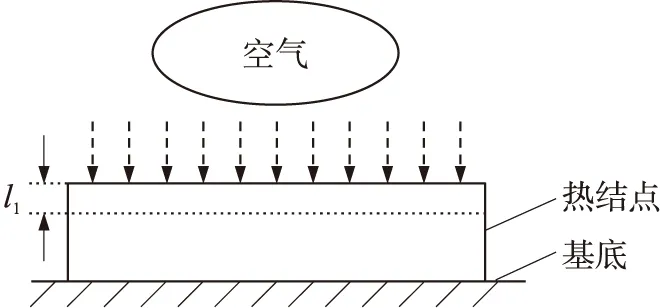
图4 激光脉冲在热结点表面作用过程

根据激光波长、功率参数及材料吸收率可确定厚度l1约为10 nm,远远小于膜厚d。激光标定的实质是向热结点表面提供一个脉冲能量Q,该能量在热结点表面转化为热能。

Q=εWtw=ρcVl(Tl-T0)=ρcVd(Td-T0)

(10)

式中ε为热结点表面对激光的吸收率,W为激光器功率,tw为激光脉冲持续时间,Vl为激光作用穿透深度l1时的体积,Tl为激光作用后热结点表面温度,Vd为热结点的体积,Td为热结点内部达到热平衡时温度,T0为热结点初始温度,即环境温度。

激光脉冲结束后,热结点暴露在空气中,可以判断此时热结点满足集总热容条件,热量由表面l1厚度的膜层内向热结点内部以热传导的形式传递,热结点在响应曲线最高点处达到温度平衡。此时传热过程如图5所示。

图5 激光脉冲结束后热结点内部传热过程

在热结点表面建立热结点表面能量平衡公式:

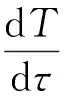
(11)

式中,k为热结点导热系数,A为热结点表面积。

初始条件设τ=0,t=t0;过余温度设θi=T-Td,则有:

(12)

对式(12)积分可得:

(13)

根据一阶系统时间常数定义,当θ/θ0=36.8%时可得τ=τ*,因此辐射换热边界条件下时间常数为:

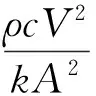
(14)

2.2.3 薄膜热电偶时间常数计算

本文采用Omega公司生产的CO1-K型薄膜热电偶进行分析及实验,热电偶相关参数lc=15.8 μm,k=20 W/(m·k),c=1.2×102J/(kg·k),ρ=18×103kg/m3,薄膜热电偶如图6所示。

图6 CO1-K型薄膜热电偶

采用水浴阶跃法进行动态标定时,水浴对流换热系数h=70 W/(m2·k),由式(9)计算可知CO1-K型薄膜热电偶时间常数为401 ms。考虑阶跃前沿理想性,薄膜热电偶投掷速度为10 m/s,热结点尺寸为300 μm×300 μm,热结点进入水浴时间为30 μs,该阶跃前沿宽度与时间常数差距非常大,可认为此时水浴提供的阶跃信号前沿理想。因此在对流换热边界条件下CO1-K型薄膜热电偶理论时间常数为401 ms。

采用激光脉冲法进行动态标定时,由式(14)计算可知CO1-K型薄膜热电偶理想时间常数为18 μs,与厂家提供时间常数一致。考虑阶跃前沿理想性,激光脉冲信号宽度为10 μs,数量级与时间常数相同,此时激光脉冲阶跃前沿不够理想,计算时间常数需要考虑前沿宽度。因此在辐射换热边界条件下CO1-K型薄膜热电偶理论时间常数应为28 μs。

图7 高速数据采集系统

3 动态标定实验及结果分析

采用水浴阶跃法、激光脉冲法两种动态标定方法来提供边界条件,激励源分别采用福禄克7341台式恒温槽和西安赫胥尔镭光纤激光器。输出热电势信号使用AD8421放大,并采用冰水混合物对热电偶进行冷端补偿。采用NI-6259数据采集卡实现最大1.25 Msample/s、16位的高速采集。实验系统如图7所示。

水浴阶跃法动态标定时,福禄克7 341台式恒温槽提供水浴阶跃信号,在水浴温度60 ℃时稳定性为±0.005 ℃,CO1-K型薄膜热电偶迅速投入水浴,采集卡采样频率为1kHz,读取数据如图8(a)所示。

图8 水浴阶跃动态标定实验曲线

根据响应曲线上升部分得出相应的Z-t曲线,对Z-t曲线进行线性拟合,见图8(b),拟合方程为:

y=-2.49×10-6x-0.001 026

(15)

将拟合曲线斜率及响应曲线跃升幅值代入式(4),即可计算出薄膜热电偶在60 ℃水浴阶跃激励下时间常数。

激光脉冲法采用西安赫胥尔镭光纤激光器提供激光脉冲,波长为980 nm,功率2 W,使用NI-6259数据采集卡提供单脉冲矩形波信号,使激光脉冲宽度为10 μs,同时使用采集卡对微纳膜厚热电偶电动势输出进行采样,采样频率为1 MHz。读取数据如图9(a)所示。

将激励响应曲线(a)上升部分得出相应的Z-t曲线,对Z-t曲线进行线性拟合,见图9(b),拟合方程为:

y=-1.639×10-6x-0.001307

(16)

将拟合曲线斜率及响应曲线跃升幅值代入式(4),即可计算出

由实验数据可知,水浴阶跃法、激光脉冲法得出实际时间常数分别为506 ms,101 μs,与理论值401 ms,28 μs比较可知,薄膜热电偶在对流换热边界条件下时间常数理论计算值接近实际计算值。针对激光脉冲激励下热电偶响应时间常数实验值与理论值偏差较大的问题,分析原因如下:①通过Z-t拟合曲线线性相关度可知,薄膜热电偶对激光脉冲的响应不能认为是理想的一阶响应曲线,采用时间常数作为薄膜热电偶在辐射换热边界下的动态特性参数本身即存在误差。②激光脉冲在热结点表面作用非常复杂,响应曲线存在较大波动,影响时间常数准确性。③激光源参数不够理想,无法提供前沿更为理想的激光脉冲,对动态标定实验结果有一定影响。

图9 激光脉冲动态标定实验曲线

4 结论

本文分析了薄膜热电偶动态标定过程中的传热过程,并对传热过程建立零维非稳态传热模型,运用集总热容法分析对流及辐射换热两种边界条件下薄膜热电偶的动态特性。与传统方法相比,集总热容法计算过程简单,适用于两种边界条件下动态特性分析。采用两种动态标定方法进行实验,对比时间常数理论值与实验值可知,对流换热边界条件下时间常数理论计算值接近实际计算值,实验值误差为25%,激光脉冲激励下热电偶响应时间常数实验值与理论值偏差较大,但是结果仍为相同数量级,通过对实验过程与理想动态标定过程的分析,可认为采用集总热容法分析薄膜热电偶动态标定过程简单,计算时间常数结果可靠。

[1] 任玲,黄凤良. 薄膜热电偶动态特性标定技术研究现状[J]. 传感器与微系统,2006,25(10):4-6.

[2]Cui Y X,Yang D S,Jia Y,et al. Dynamic Calibration of the Cutting Temperature Sensor of NiCr/NiSi Thin-Film Thermocouple[J]. Chinese Journal of Mechanical Engineering,2011,24(1):73-77.

[3]杨丽红,赵源深,陈皓帆,等. Cu/CuNi薄膜热电偶动态特性理论与实验研究[J]. 中国机械工程,2013,24(10):1336-1339.

[4]马旭轮,苑伟政,马炳和,等. CFCC-SiC基底NiCr/NiSi薄膜热电偶制备及性能研究[J]. 传感技术学报,2014,27(3):304-307.

[5]杨遂军,邬云晨明,于方舟,等. 基于电子印刷工艺的薄膜热电偶研制[J]. 传感器与微系统,2014,33(1):85-88.

[6]赵源深,杨丽红. 薄膜热电偶温度传感器研究进展[J]. 传感器与微系统,2012,31(2):1-3,7.

[7]崔云先. 瞬态切削用NiCr/NiSi薄膜热电偶测温刀具研究[D]. 大连:大连理工大学,2011.

[8]曾其勇,郑晓峰,吴凯,等. 基于薄膜热电偶的高速切削动态温度监测系统设计[J]. 仪表技术与传感器,2011,(6):96-98,101.

[9]杨丽红,赵源深. 基于尺寸效应的Cu/CuNi薄膜热电偶灵敏度研究[J]. 电子元件与材料,2011,30(11):16-18.

[10]Chen Y X,Jiang H C,Zhao W Y,et al. Fabrication and Calibration of Pt-10%Rh/Pt Thin Film Thermocouples[J]. Measurement,2014,(48):248-251.

[11]黄吕权,李付国. 薄膜热电偶的技术特性研究[J]. 中国机械工程,1996,7(5):34-36,123.

[12]吕鹏飞,裴东兴,沈大伟. 基于K型热电偶的瞬态测温技术的研究[J]. 传感技术学报,2014,27(6):775-780.

王晓娜(1975-),女,2004年于浙江大学获工学硕士学位,现为中国计量学院测控技术与仪器专业副教授,主要研究方向为几何量精密测量和光电检测技术,wangxn@cjlu.edu.cn;

叶树亮(1973-),男,2005年于哈尔滨工业大学获工学博士学位,现为中国计量学院精密仪器专业教授,主要研究方向为化工产品安全测试技术与仪器、工业零部件缺陷检测技术与设备、精密测量中部件信号处理与误差分析技术,itmt_paper@126.com。

StudyofTFTCDynamicCharacterBasedonLumpedCapacitanceMethod*

WANGXiaona,YUFangzhou,YANGSuijun,QIManyu,YEShuliang*

(Institute of Industry and Trade Measurement Technology,China Jiliang University,Hangzhou 310018,China)

In order to analyze dynamic character of thin-film thermocouple(TFTC)under different heat transfer boundary conditions,a zero dimensional heat transfer model is established on TFTC transient temperature measurement process. The lumped capacitance method is used to analyze thin-film thermocouple’s heat transfer process under convective heat transfer and radiative heat transfer boundary conditions. TFTC dynamic character theoretical parameter is calculated by the establishment of the energy balance on the surface of hot junction. Water bath step method and laser pulse method are used for dynamic calibration on CO1-K thermocouple,the experimental dynamic character parameter of the sensor is obtained byZ-ttransform on the dynamic response curve. The experiment results show that the lumped heat capacity method can be used correctly to analyze the dynamic character of thin-film thermocouple. The thin-film thermocouple time constant under different boundary conditions is simple to calculate. The theoretical time constant is close to the experimental.

thin-film thermocouple;dynamic character;zero dimensional heat transfer model;the lumped capacitance method;dynamic character calibration

项目来源:国家质检公益性行业科研专项项目(201310102-1)

2014-08-01修改日期:2014-10-29

TP274

:A

:1004-1699(2014)12-1627-05

10.3969/j.issn.1004-1699.2014.12.008