Improvement of Temperature Compensation Calculated Value for FBG Strain Sensor*

HOU Liqun，ZHAO Xuefeng，LENG Zhipeng，SUN Tao

(1.School of Civil Engineering and Architecture，Northeast Dianli University，Jilin 132012，China; 2.School of Civil Engineering，Dalian University of Technology，Dalian Liaoning 116024，China; 3.Ningbo Shangong Center of Structural Monitoring and Control Engineering Co.，Ltd，Ningbo Zhejiang 315177，China; 4.China Tienchen Engineering Corporation，Tianjin 300000，China)

Improvement of Temperature Compensation Calculated Value for FBG Strain Sensor*

HOU Liqun1*，ZHAO Xuefeng2，LENG Zhipeng3，SUN Tao4

(1.School of Civil Engineering and Architecture，Northeast Dianli University，Jilin 132012，China; 2.School of Civil Engineering，Dalian University of Technology，Dalian Liaoning 116024，China; 3.Ningbo Shangong Center of Structural Monitoring and Control Engineering Co.，Ltd，Ningbo Zhejiang 315177，China; 4.China Tienchen Engineering Corporation，Tianjin 300000，China)

The conventional temperature compensation algorithms do not consider the difference between sensor calibration condition and actual test condition，therefore it is deficient in the theoretical aspect.In order to solve the above problem，the restrained deformation characteristics and temperature influence of the sensors under test condition were analyzed，and then an improved algorithm for temperature compensation was proposed.The correctness of the algorithm was verified bymeans of theoretical analysis and strain test on a concrete block.Theoretical analysis shows that the proposed algorithm has considered the influence from the difference of the linear expansion coefficient between the sensor and measured structure.Therefore，the improved algorithm is theoreticallymore reasonable.Test result shows that the strain calculation error from the improved algorithm is less than 4με，however the error from the conventional algorithm ismore than 8με.The improved algorithm is correct in the theoretical aspectwith higher accuracy，and can be applied in practical projects.

fiber Bragg grating(FBG);temperature compensation;strain test;linear expansion coefficient

光纤布拉格光栅应变传感器由于具有精度高、耐久性极强、抗腐蚀、抗电磁干扰以及可测动应变等优良特性，在结构健康监测应变测量中得到了广泛的应用。但由于光纤光栅应变传感器存在应变和温度的交叉敏感问题［1－2］，需采用温度补偿技术对应变传感器测试数据进行修正。温度补偿技术包括两类:(1)利用温度补偿算法进行数据处理［3－6］;(2)设计特殊的传感器结构实现传感器温度自补偿［7－15］。尽管第2类技术研究的较多，但工程中目前普遍采用第1类技术。传统的温度补偿算法没有考虑传感器的标定状态和实际测试状态的差别，直接利用传感器室内标定的温度灵敏度系数进行温度补偿，忽略了光纤光栅应变传感器本身的线膨胀系数和被测结构线膨胀系数的差别所带来的影响，在温度变化较大时将带来显著的误差。本文对传统温度补偿算法进行了改进，并通过理论分析和混凝土试块应变测试试验验证了该改进算法的正确性。

1 光纤光栅传感基础理论

光纤光栅是指单模掺锗光纤经紫外光照射形成的光纤Bragg光栅，成栅后的光纤纤芯折射率呈现周期性分布条纹并产生光栅效应。由耦合模理论可知，光纤Bragg光栅的中心波长λB可表示为式(1)［1－3］:

式中:neff为芯层导膜有效折射率;Λ为光栅栅距周期。

应力引起FBG波长漂移公式为(2)［1－3］:

应力作用下光弹效应导致neff变化，变形导致Λ变化，假设在温度不变的条件下，光纤受到均匀轴向应力产生应变变化Δε时，光栅中心波长的漂移ΔλB(ε)与光纤光栅轴向应变变化Δε的关系为式(3)［1－3］:

式中:k为应变影响系数，对于某一光栅来说是常数。对于封装后的传感器，ΔλB(ε)=KS·Δε，式中:KS为应变灵敏度系数(pm/με)。

温度对波长的影响来源于热光效应引起的neff改变及热膨胀效应引起的Λ改变。当仅存在温度变化的条件下，光栅中心波长的漂移ΔλB(T)与温度变化ΔT的关系为式(4)［1－3］:

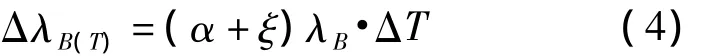
式中:α为光纤线性热膨胀系数;ξ为光纤热光系数。对于封装后的传感器，ΔλB(T)=()· ΔT，式中:为只考虑热光效应的温度灵敏度系数(pm/℃)为只考虑温度引起传感器变形的温度灵敏度系数(pm/℃)。设KTS为总温度灵敏度系数，则K。

当应变和温度同时发生变化时，实际测到的光纤光栅应变传感器的波长数据将包含应变和温度的共同影响，光栅中心波长的漂移ΔλB与应变Δε及温度变化ΔT的关系为式(5)［1－3］:

式中:ξλB·ΔT是温度热光效应导致的光栅波长改变，而(kλB·Δε+αλB·ΔT)是光栅变形导致的波长改变(包括荷载引起的变形和温度引起的变形)。

由式(5)可知，只基于传感器的波长改变无法分离应变和温度的影响，因此在实际工程测量中需同时测量光纤光栅应变传感器的温度变化，并通过数据处理的方式去除温度对该类传感器应变测量值的影响，即进行温度补偿。

2 温度补偿传统算法的不足

目前工程中普遍应用的光纤光栅应变传感器的温度补偿传统算法如式(6)所示:

式中:KS为应变灵敏度系数(pm/με);Δε(L)为荷载(包括约束反力)引起的应变变化量(με)，可直接求取应力，即Δσ=E·Δε(L);ΔλB为光纤光栅应变传感器中心波长总的变化量(pm)。式(6)中KS和KTS来自于实验室标定，因此KTS·ΔT是传感器在标定状态下温度变化ΔT时导致的中心波长的变化量，而并非在测试状态下温度变化ΔT时导致的中心波长的变化量。KTS标定通常采用水域法，传感器可在水域中自由伸缩，而当传感器安装于被测结构时，其处于约束状态，无法随温度变化自由伸缩，变形只能受制于被测结构，此时如仍采用标定试验得出的KTS进行计算显然是不合适的。

3 温度补偿传统算法的改进

事实上测试状态下传感器的波长测量值变化ΔλB包含如下几个部分:

(1)结构测点的真实应变量Δε(A)(也是传感器的真实变形量)引起波长变化量ΔλB(A)，其中Δε(A)又包含两部分:a)由温度变化ΔT引起的名义自由温度伸缩应变Δε(T0)，Δε(T0)=αc·ΔT，其中αc为被测结构的线膨胀系数(με/℃)。;b)由荷载及约束反力引起的约束应变Δε(L)，当结构完全无约束且无外力时Δε(L)=0，当结构被完全约束无法变形时Δε(L)=－Δε(T0)=－ΔT，此时Δε(A)=0。

(2)只考虑热光效应的情况下，温度变化ΔT导致的传感器的波长测量值变化量ΔλB(T1)，请注意ΔλB(T1)=KⅠ

TS·ΔT，而不是ΔλB(T1)=KTS·ΔT，由于在测试状态下，传感器的变形受制于结构，相当于传感器的自由温度伸缩应变被Δε(T0)取代，因此传感器温度变形导致的传感器的波长测量值变化量ΔλB(T2)已计入ΔλB(T0)中，无需重复计算。综合上述分析可得:

考虑到标定时传感器处于无约束自由伸缩状态，可得KⅡTS=KSαS，式中:αS为传感器的线膨胀系数(με/℃)。考虑到，代入式(7)，整理可得改进后的光纤光栅应变传感器的温度补偿算法:

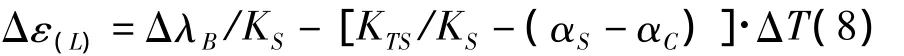
式(8)中ΔλB/KS为未进行温度补偿的应变计算值，［KTS/KS－(αS－αC)］·ΔT为改进算法的应变温度补偿值，而式(6)中(KTS/KS)·ΔT为传统算法的应变温度补偿值，比较式(6)和式(8)可知，改进后算法与传统算法应变温度补偿值相差(αS－αC)·ΔT，当αC=αS时，改进后算法与传统算法是一致的。

目前工程中应用的光纤光栅应变传感器的封装方式主要有两种:钢管封装和GFRP封装(玻璃纤维增强树脂封装)。GFRP封装与钢管封装相比，最显著的优势是抗腐蚀性好，耐久性强，可满足结构健康监测系统长期监测的需要。对于钢管封装的光纤光栅应变传感器，由于钢管热膨胀系数与混凝土或钢结构的热膨胀系数基本相同，因此αC=αS，由式(6)和式(8)比较可知传统算法与改进算法一致。但对于GFRP封装的光纤光栅应变传感器，GFRP的线膨胀系数通常取8με/℃，被测混凝土结构或钢结构的线膨胀系数通常取12με/℃，当温度变化ΔT= 20℃时，(αS－αC)·ΔT=(8－12)×20=－80με，当温度变化ΔT=50℃时，(αS－αC)·ΔT=－200με，这种误差无论对于混凝土结构，还是钢结构，都是不可接受的。

4 试验验证

为了验证改进后算法的合理性和正确性，设计了如下试验:将1支GFRP封装光纤光栅应变传感器和1支光纤光栅温度传感器埋入混凝土试块中的同一位置，将混凝土试块无约束地放置在实验室内，连续采集3天数据，通过数据分析进行算法验证。

实验室内的昼夜温差在2℃以内，由光纤光栅温度传感器实测的混凝土试块内部温度曲线如图1所示。

图1混凝土试块内部温度曲线

图2 给出了按传统算法和改进算法计算的温度补偿值时程曲线。由于混凝土试块无约束，理论上Δε(L)应该等于0，即未进行温度补偿的应变计算值应该等于应变温度补偿值。由图2可以看出，与传统算法的应变温度补偿值(KTS/KS)·ΔT相比，改进算法的应变温度补偿值［KTS/KS－(αS－αC)］·ΔT与未进行温度补偿的应变计算值ΔλB/KS更接近，这说明改进算法的计算结果更接近与理论值，因此更合理和准确。

图2按传统算法和改进算法计算的温度补偿值的比较

图3 给出了按传统算法和改进算法计算的约束应变值，可以看出，改进算法计算的约束应变误差的变化范围在4με以内，而按传统算法计算的约束应变误差的变化范围已超过8με，因此改进算法的计算结果更准确。由于本次试验中环境温度变化较小，因此两种算法的差异并不是很大，在实际监测中，环境温度变化可能达到40℃以上，那时两种算法的差异将非常显著。

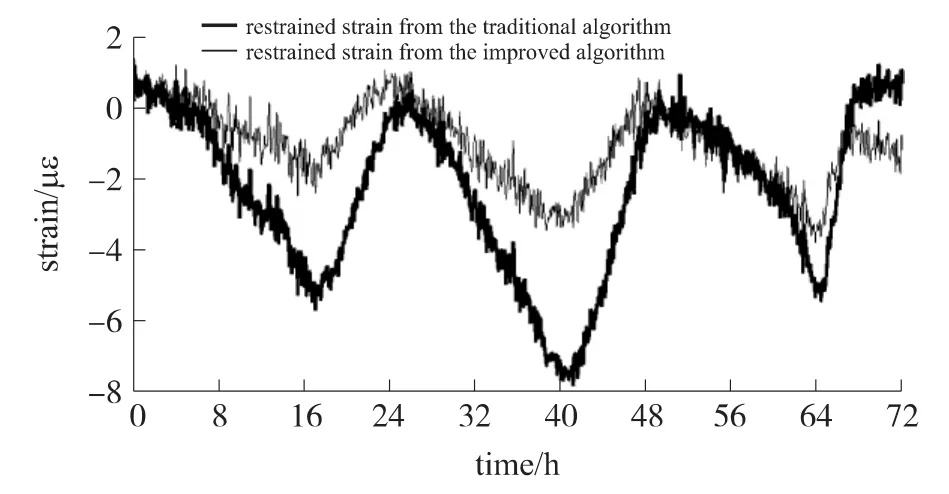
图3 按传统算法和改进算法计算的约束应变值的比较

由于测试误差及标定误差的存在，以及应变传感器和温度传感器感受到的温度未必完全一致，导致按改进算法计算的约束应变仍残留部分温度影响，在实际工程中，往往应变传感器和温度传感器不是一对一布置在同一位置，因此这种残留温度影响的现象更为严重，本文中给出的改进算法可在一定程度上削弱温度的影响，但无法全部消除。

5 结论

本文分析了光纤光栅应变传感器标定状态与实测状态的差别，指出了其温度补偿传统算法的不足，给出了改进算法，并进行了试验研究，结论如下:

(1)传感器实测状态下其变形受制与被测结构，但其标定时处于自由状态，因此直接利用标定得出的温度灵敏度系数KTS进行温度补偿误差较大;

(2)由于温度导致的传感器变形已包含在被测结构的变形中，因此温度补偿时只需考虑KⅠTS，基于此提出了温度补偿改进算法，该算法在理论上更严谨和合理;

(3)对于钢管封装的光纤光栅应变传感器，由于αC=αS，因此改进算法与传统算法一致，而对于GFRP封装的光纤光栅应变传感器，由于αC≠αS，因此改进算法与传统算法的计算结果相差(αS－αC)· ΔT，当温度变化较大时，这个差异很显著;

(4)混凝土试块试验表明，利用改进算法得到的实测应变误差小于4με，而利用传统算法得到的实测应变大于8με，改进算法计算的结果更加接近与理论值;

(5)由于测试误差、标定误差以及被测结构温度场不均匀，导致温度补偿算法只能部分削弱温度效应，不能完全去除。

［1］魏鹏，李丽君，郭俊强.光纤Bragg光栅应力传感中温度交叉敏感问题研究［J］.应用光学，2008，29(1):105－109.

［2］李爱群，周广东.光纤Bragg光纤传感器测试技术研究进展与展望(I)［J］.东南大学学报(自然科学版)，2009，39(6):1298－1306.

［3］赵启林，杨洪，陈浩森.光纤光栅应变传感器的温度补偿［J］.东南大学学报(自然科学版)，2007，37(2):310－314.

［4］宁辰校，张戌社.光纤光栅温度补偿实验研究［J］.河北科技大学学报，2006，27(2):155－157.

［5］万里冰，王殿富.基于参考光栅的光纤光栅应变传感器温度补偿［J］.光电子·激光，2006，17(1):50－53.

［6］郑卜祥，宋永伦，张东生.光纤Bragg光栅温度和应变传感特性的试验研究［J］.仪表技术与传感器，2008(11):12－15.

［7］李国利，李志全.光纤光栅应变传感测量中的温度补偿问题［J］.激光与光电子学进展，2005，42(4):25－27.

［8］薛俊华，李川，陈富云，等.低温敏的双管式光纤Bragg光栅应变传感器的研究［J］.传感技术学报，2012，25(10):1387－1391.

［9］黄勇林，董兴法，董孝义.光纤布拉格光栅温度补偿研究［J］.激光杂志，2005，26(6):68－69.

［10］郭子学，闫卫平，杜国同.光纤Bragg光栅温度补偿方法的研究［J］.光电子技术，2006，26(1):48－52.

［11］姚远，易本顺，肖进胜.光纤布拉格光栅传感器的温度补偿研究［J］.应用激光，2007，27(3):191－200.

［12］王俊杰，刘波，张丰涛，等.基于温度补偿方法去敏的新型光纤光栅压力传感器［J］.仪器仪表学报，2009，30(11):2342－2346.

［13］李维善，陈琛，王海林.基于Bragg光栅交叉法在温度补偿中的研究［J］.仪表技术与传感器，2011(6):87－88，92.

［14］王为，林玉池.表面式温度补偿型光纤光栅传感器研究［J］.半导体光电，2009，30(3):362－365，370.

［15］郑建邦，刘嘉，任驹，等.一种免受温度影响的双光纤光栅应变传感器［J］.传感技术学报，2006，19(6):2411－2413，2417.

侯立群(1980－)，男，黑龙江省延寿县，博士，高级工程师。2009年04月毕业于哈尔滨工业大学，获工学博士学位，导师欧进萍院士，专业为工程力学，研究方向:结构健康监测。目前为东北电力大学专任教师，主要从事结构健康监测方面的研究，hlq_work@sina.com。

光纤光栅应变传感器温度补偿计算值的改进*

侯立群1*，赵雪峰2，冷志鹏3，孙涛4

(1.东北电力大学建筑工程学院，吉林吉林132012;2.大连理工大学土木工程学院，辽宁大连116024; 3.宁波杉工结构监测与控制工程中心有限公司，浙江宁波315177;4.中国天辰工程有限公司，天津300000)

温度补偿传统算法没有考虑光纤光栅应变传感器标定状态和实际测试状态的差别，在算法理论上存在不足。为解决这一问题，分析了测试状态下传感器的约束变形特征及温度影响，提出了温度补偿改进算法。通过对改进算法和传统算法的比较分析以及混凝土试块应变测试试验，验证了算法的正确性。理论分析表明，改进算法体现了传感器本身的线膨胀系数和被测结构线膨胀系数的差别所带来的影响，理论上更合理。混凝土试块应变测试试验结果表明，利用改进算法得到的实测应变误差小于4με，而利用传统算法得到的实测应变大于8με。改进算法理论正确，计算结果精度更高，具有工程实用性。关键词:光纤光栅;温度补偿;应变测试;线膨胀系数

TN212.14

A

1004－1699(2014)01－0070－04

2013－03－10修改日期:2013－06－08

C:7220;7230E

10.3969/j.issn.1004－1699.2014.01.013

项目来源:国家自然科学基金青年基金(51308094);国家自然科学基金面上项目(51278085);国家十二五科技支撑计项目(2011BAK02B02);东北电力大学博士科研启动基金项目(BSJXM－201222)