高效能ESCA协处理器验证技术研究＊

邓承诺，吴 丹，黄 威，戴 葵，邹雪城

（华中科技大学电子科学与技术系，湖北 武汉430074）

1 引言

随着VLSI技术的进步，单芯片所能提供的丰富晶体管资源使得微处理器规模越来越大。而随着微处理器规模的增大，体系结构日益复杂，多采用乱序执行、多级流水、中断、例外处理以及多级存储结构等技术，使得处理器的验证复杂度不断增加。

在现代集成电路设计中，功能验证所花的时间大概要占60%，功能验证已经成为大规模集成电路设计的瓶颈［1］。用最少的验证案例达到最大的验证覆盖率，尽可能地降低验证成本和处理器面世时间是处理器验证领域研究的核心问题。国内外对于加速处理器验证和提高处理器验证的完备性，做了很多相关研究，如验证向量的自动生成［2］、形式化验证技术［3］和覆盖率分析［4］等。形式化验证方法通过数学证明验证系统的正确性，一般只用于规模不大的模块级设计验证；模拟方法用模拟矢量对 HDL（Hardware Description Language）描述的RTL（Register Transfer Level）模型进行模拟运行。目前，由于模拟验证方法比较成熟，能适应规模越来越大的微处理器架构，因此仍然是微处理器验证的主要手段。但是，不论是定向验证激励的产生还是随机验证激励的自动生成，都只有在验证方法学的指导下针对每个功能单元的特性，才能生成高效率的验证案例，这正是本文要研究的内容。

本文借鉴软件验证的思想，将软件功能验证［5］中的边界值验证、等价类验证和基于决策表的验证应用于处理器验证中，提出了一种针对微处理器不同功能部件特点设计微处理器综合验证方案的方法。该方法在完全实现微处理器验证目标的同时，有效地缩短了验证时间，提高了验证效率，并已经成功应用于一款高效能协处理器ESCA的验证中。

2 处理器验证方法

微处理器验证的目的是用最少的验证案例覆盖最大的待测功能，保证所有体系结构功能的正确性。本文主要采用基于模拟的验证方法，通过模拟验证案例集来验证体系结构功能。验证案例集一般包括随机生成和手工生成的验证案例，以及实际的应用程序工作负载。通过功能验证方法指导验证案例的手工生成和随机验证案例生成的约束条件，可提高验证的覆盖率和有效性。

功能验证方法主要包括边界值验证、等价类验证和基于决策表的验证。

2.1 边界值验证法

边界值验证法通过考察输入变量范围的边界值来构造验证案例，衍生出四种技术：边界值分析法、健壮性验证法、最坏情况验证法和健壮最坏情况验证法。

（1）边界值分析法。边界值分析法利用输入变量的最小值、略大于最小值的值、正常值、略小于最大值的值和最大值处的取值来构造验证案例，并分别记为 min、min＋、nom、max－、max。图1a所示是当两个输入变量x1∈［a，b］，x2∈［c，d］时的验证案例选择。当n个变量参与边界值分析时，会产生4n＋1个不同的验证案例。

（2）最坏情况验证法。最坏情况验证推翻单故障假设，考察多个变量同时取极值的情况，对min、min＋、nom、max－、max五个基本值取笛卡尔积构造验证案例，如图1b所示。对n个变量的验证对象，会产生5n个验证案例。最适合采用最坏情况验证的场合是各个物理变量之间存在大量的相互作用，而且函数失效的代价极高。

（3）健壮性验证法。健壮性验证在边界值分析法的基础上，考察了略大于最大值（max＋）的值和略小于最小值（min－）的值，如图1c所示。对于n个输入的验证对象，验证状态集合数为6n＋1。由于健壮性验证把验证的注意力部分集中在系统对异常情况的处理上，如例外和中断处理，适用于存在大量异常处理的情况。

（4）健壮最坏情况验证法。当对验证有特别极端的要求时，可以采用健壮最坏情况验证法。构造了七个基础值的笛卡尔积，如图1d所示。对于n个输入的验证对象，验证工作集的大小是7n。

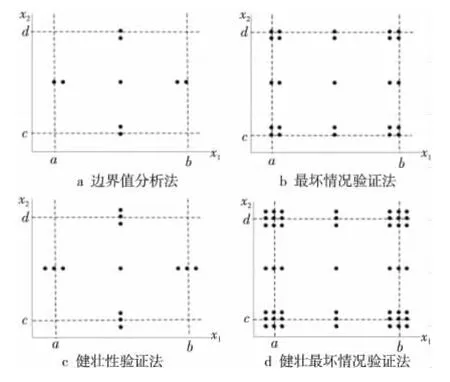
Figure 1 Boundary value verification cases of bivariate object图1 双变量验证对象的边界值验证案例示意图

2.2 等价类验证法

等价类验证法即根据输入数据（或输出状态）的特性将其划分为不同的等价类，在保证微处理器对于同一等价类的数据的处理相同的前提下，在一个等价类中选择一个或多个关键数据构成验证案例集。采用等价类验证方法可很好地避免冗余，使验证条理清晰，找到遗漏。

从是否遵从单故障假设和是否关注无效数据和异常机制两方面，分为四种等价类验证案例构造方法，如图2所示，分别对应：

（1）弱一般等价类验证：基于单故障假设且不考虑无效值；

（2）强一般等价类验证：基于多故障假设且不考虑无效值；

（3）弱健壮等价类验证：基于单故障假设且考虑加入无效值；

（4）强健壮等价类验证：基于多故障假设且考虑加入无效值。

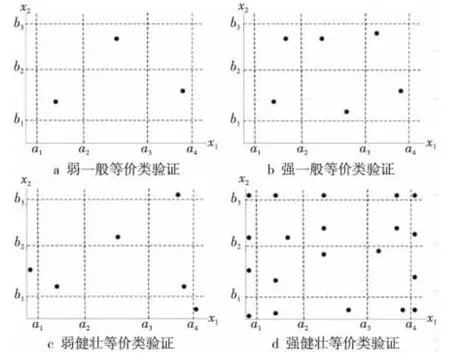
Figure 2 Equivalence class verification cases bivariate object图2 双变量验证对象的等价类验证案例示意图

2.3 基于决策表验证法

基于决策表验证法是所有功能验证法中最严格的，通过强化逻辑严密性，保证验证的完整性和有效性。

该验证法是通过分析被测程序各个功能之间的逻辑依赖关系编写决策表，基于决策表生成验证案例。如表1所示，决策表的桩条件项C1、C2、C3为输入的等价类；桩动作项A1、A2、A3为处理器的功能；规则项为验证案例；T／F表示是否满足桩条件；“—”表示无关项，解释为条件无关或不适用。

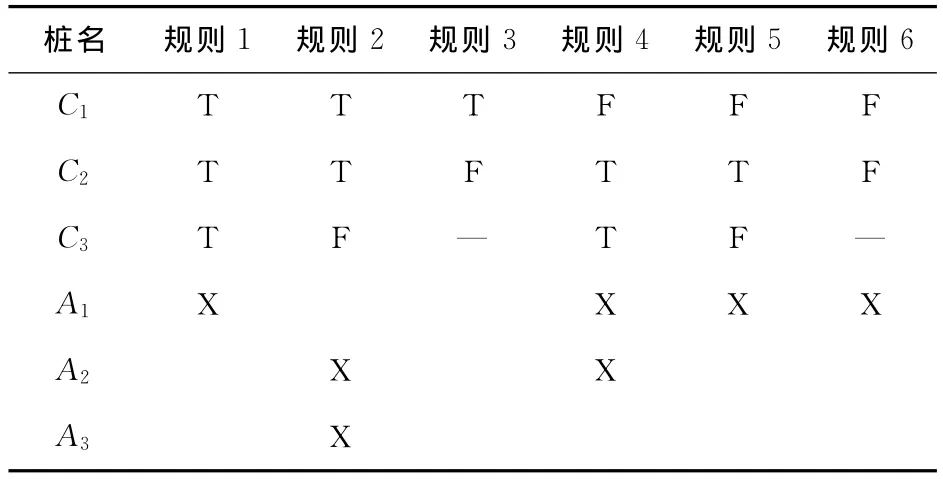
Table 1 Rule of decision table verification表1 决策表示意图

对于n个桩条件，对应有2n个规则，而每出现m个无关项“—”规则项可扩展成2m个规则项。如表1所示，对应C1、C2、C3三个桩条件，应有八个规则项，而规则3、规则6分别相当于两个规则项，故合并后的决策表共有六个规则项。“X”代表适用对应的动作。

2.4 综合验证方法的选择

针对微处理器不同功能部件的特点，微处理器综合验证方法可结合上述三种验证方法，采用基准验证法结合辅助验证法，生成高效的验证案例。

首先，根据待测功能单元输入变量间是否存在依赖关系、是否遵从单故障假设以及是否存在大量的异常处理，根据表2选择基准验证方法。在表2中，C1、C2、C3是三个判断的桩条件，A1～A9是九个对应处理的桩动作项，由三个桩条件可得出8个规则项，又由于规则5中无关项的存在，共有五个规则项。

其次，在基准验证方法的基础上，根据验证对象灵活选取辅助验证方法。以规则5为例，在C1条件不满足、输入不是独立变量的情况下，只有A9决策表验证法能被选作基准验证方法，而此时结合A1边界值分析法能验证决策表中的规则边界情况，因此选为辅助验证方法，能提高验证的覆盖率。

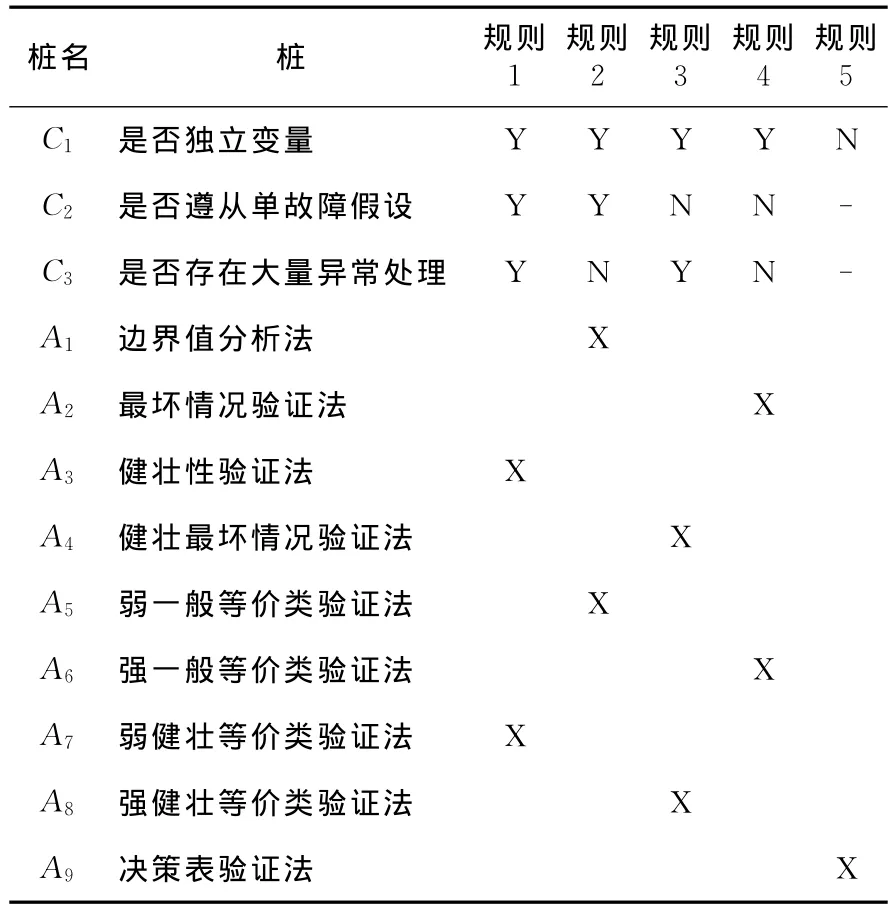
Table 2 Selection of function verification method表2 功能验证方法的选择

3 高效能ESCA协处理器体系结构

ESCA（Engineering and Scientific Computing Accelerator）［6］是一款64位的高效能加速协处理器，它与通用处理器一起组成计算系统，基于主－协处理器协同工作的混合计算方式实现程序加速。其中协处理器ESCA采用单指令流多数据流SIMD（Single Instruction Multiple Data）的执行方式，并行执行工程与科学计算应用中可并行的核心程序，主机（HOST）执行串行的计算指令和调度、分配任务。

ESCA主要针对的典型工作负载（Work Load）为科学计算、多媒体和数据库等，其指令集结构分为三大类。其中，控制类指令主要包括条件、条件中断、分支和系统控制及同步；数据传输类指令主要包括ESCA芯片和外部的Load／Store指令、计算阵列中PE以及组之间的数据传输指令；计算类指令主要包括定点ALU指令、定点逻辑指令和浮点指令。ESCA指令集采用128位定长固定格式指令编码，指令中包含指令编码、PE选择掩码、寄存器块选择掩码及源、目的操作数。

4 高效能ESCA协处理器验证案例构造

以具体的待测单元IALU、FMAC、DMA Engine为例，针对不同单元的特性，选择合适的方法指导验证案例的手工生成和随机验证案例生成的约束条件。

定点算术逻辑单元IALU指令，有两到三个操作数输入，操作数间无依赖关系，两输入值之间、输入寄存器之间、以及输入值和寄存器之间无大量的相互作用，遵从单故障假设，有上溢、下溢等简单的异常处理，属于表2中的规则项2。故基准验证法可采用边界值分析法，辅助验证法采用健壮性验证法进行异常与中断验证的补充。

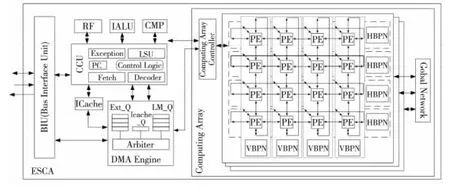
Figure 3 Diagram of ESCA system structure图3 ESCA系统结构框图

多精度浮点功能单元FPU指令，与基本定点运算单元指令类似，操作数间无依赖关系且遵从单故障假设，但边界情况多样化，有非数、非规格数、正负无穷大等多种边界，以及大量异常，属于表2中的规则项1，适合进行等价类划分。故基准验证法采用弱健壮等价类验证法，辅助验证法采用边界值分析法对等价类的划分边界进行补充验证。

直接存储访问单元DMA Engine功能单元有18个输入参数，输入间有逻辑依赖关系，如根据广播开启位决定具体计算PE参数的采用与选择；根据读写控制位决定读写掩码的选择来源，属于表2中的规则项5。基准验证法采用决策表验证法，辅助验证法采用强一般等价类验证法将输入状态归类以帮助生成决策表，并采用边界值分析法补充验证决策表每个规则项的边界情况。

4.1 边界值验证法构造IALU验证案例

IALU的基准验证法（边界值分析法）的取值点为 min、min＋、nom、max－、max，IALU的输入包括操作数和操作数来源。以定点byte加为例，操作数分别用0x80、0x81、0x15、0x7e、0x7f来代入，对于操作数来源（寄存器名称），则用R0、R1、R100、R254、R255代替。

从其鹿编来到编辑部的那天起，就注定要走上一条麻辣的不归之路。以前能接受的带有“麻辣”二字的食物只有麻辣拌、麻辣香锅和麻辣小龙虾，然后在外卖单上备注：不辣。刚来编辑部的时候，吃辣还吃得挺开心，直到有一天其鹿编吃了一块不知什么品种的辣椒，开始不停地打嗝。以后只要看到小小的、油亮的红色的东西，就不敢下筷子。后来还发现，经常吃辣还会让脸长一种痘，而且很难消下去。所以其鹿编现在几乎告别食辣了，但如果有哪位意丝未来想要成为编辑部的一员，可要学会吃辣呀，因为吃辣可以刺激食欲，编辑部的工作多得很，要多多吃饭以保存体力。

IALU的辅助验证健壮性验证法用来补充异常和中断验证，加入min－、max＋两个取值点，此时对于操作数而言，没有可以取值的对应点，对于操作数来源，加入验证点R－1、R256。

4.2 等价类验证法构造FMAC验证案例

根据IEEE754［7］的标准，输入数据分为非数集合DNaN、｛－∞｝、负的规格化非零浮点数集合Dnn、负的非规格化浮点数集合Dnd、｛－0｝、｛＋0｝、正的非规格化浮点数集合Dpd、正的规格化非零浮点数集合Dpn、｛＋∞｝。从输出结果的角度，IEEE754标准定义了五种异常：无效操作、被零除、上溢、下溢、结果不精确。

对于基本浮点运算指令，从输入数据的角度，输入验证状态Din［8］为：

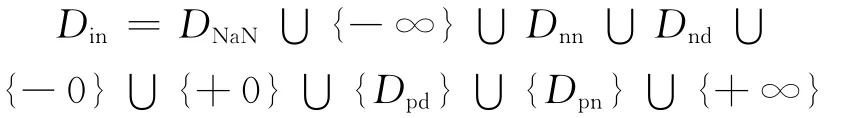
在输出域的角度，将上述五种异常和正常情况对应的关键数据集合分别记为：IOKEY、DZKEY、OFKEY、UFKEY、INEKEY、NORKEY，则输出域验证集合RoutKEY为：

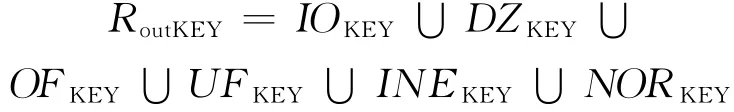
输入输出域的验证状态集合DinKEY×RoutKEY即为满足要求的验证案例集。

对于以上的等价类划分，基准验证法采用弱健壮等价类验证法，在每个等价类中选取相应的验证点，并结合辅助验证法边界值分析法，对于每个等价类如｛Dpn｝等，分别选取此类的边界点加入验证案例。

4.3 决策表验证法构造DMA功能单元验证案例

首先将DMA Engine输入参数划分等价类，根据广播与否、读写情况、操作数由立即数或寄存器提供以及数据在buffer0或buffer1中操作几个条件将验证空间划分为16块。如图4所示，实心圆点对应强一般等价类验证案例，空心圆点对应弱一般等价类验证案例。

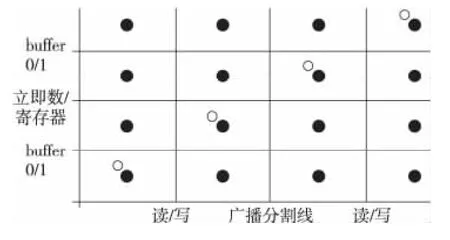
Figure 4 Division of equivaence class for DMA verification图4 DMA验证的等价类划分

在等价类划分的基础上，同样根据广播与否、读写情况、操作数由立即数或寄存器提供以及数据在buffer0或buffer1中操作几个条件编写决策表，如表3所示。

考虑到无关项，共有12个规则项。根据决策表，对应每个规则项生成相应的验证案例。再采用边界值分析法对于每个规则项对应的起始地址、传输长度、传输跳步与读写掩码生成辅助的验证案例。

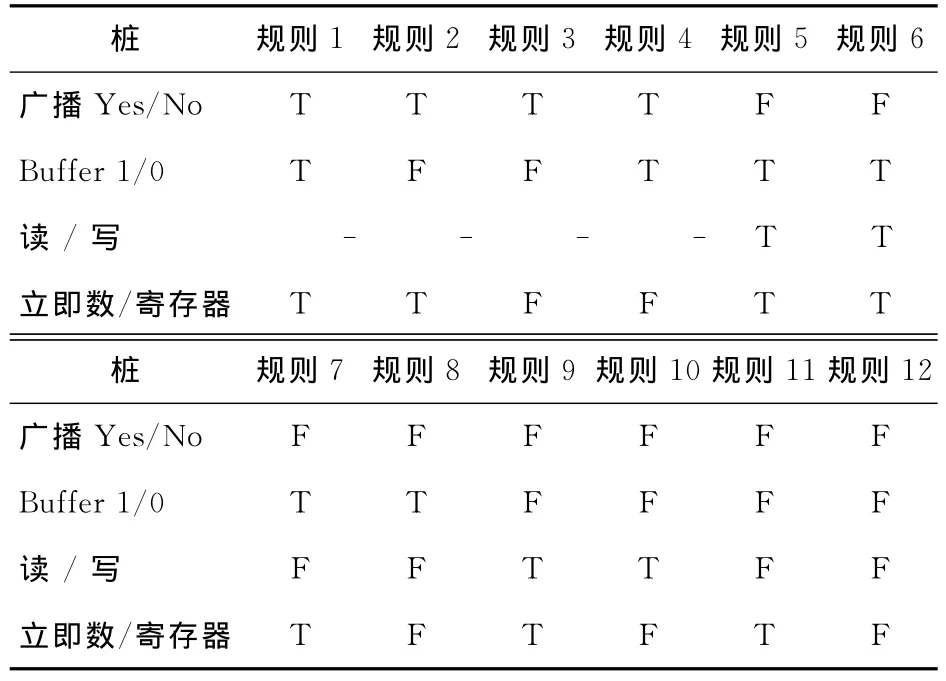
Table 3 Decision table verification cases of DMA fuction units表3 DMA Engine功能单元决策表验证案例

5 高效能ESCA协处理器验证结果评测

针对高效能ESCA协处理器的不同功能单元，据其具体特性，可采用综合验证法生成验证案例，如表4所示。基准验证法与辅助验证法结合的综合验证法，在达到功能验证目的的同时，能缩短验证时间并减少验证工作量。

Table 4 Comprehensive verification method of function units表4 功能单元综合验证法

全完备验证是遍历所有的验证状态、每一个操作数可能的取值得到的验证案例集。如图5所示，综合验证法与全完备验证相比，验证数量和效率得到了大幅提升。在设计仿真后期，由于验证激励要反复使用，以验证不断修改完善的处理器功能的正确性，因此高效的验证案例集节约了大量的验证时间，并能同时保证验证的完备性和覆盖率［9］。

6 结束语

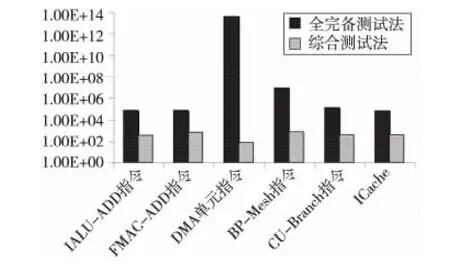
Figure 5 Verification cases scale comparison of function units图5 部分功能单元验证案例规模比较

处理器的功能验证是非常复杂的系统工程，在ESCA处理器的验证中，主要采用了基于模拟的验证方法，通过设计方案与C语言实现的黄金参考模型构建的自动验证平台完成验证流程。本文主要在边界值验证法、等价类验证法、决策表验证法的基础上，提出了一种针对微处理器不同功能部件特点设计微处理器综合验证案例的方法，探讨不同功能单元的综合验证方法对应的基准验证方法与辅助验证方法，并在与全完备验证的比较中验证其高效性。本文给出的综合验证法通过实际验证保证功能100%验证，覆盖指令集所有指令和每条指令的异常、正常执行情况，发现了浮点功能单元的精度误差、异常处理错误等问题，以及DMA和网络部分的跳步、掩码错误等问题，进行了及时的更正，保证了流片的成功。

［1］ Evans A，Silburt A.Functional verification of large ASICs［C］∥Proc of the 35th Design Automation Conference，1988：650－655.

［2］ Aharon A，Goodman D.Test program generation for functional verification of power PC processors in IBM［C］∥Proc of the 32nd Design Automation Conference，1995：279－285.

［3］ Wang Hai－xia.Research on formal methods in arithmetic circuit verification［D］.Beijing：Institute of Computing Technology，2004.（in Chinese）

［4］ Benjamin M.A study in coverage－driven test generation［C］∥Proc of the 36th Design Automation Conference，1999：970－975.

［5］ Jorgensen P C.Software testing：A craftman’s approach［M］.Boca Raton：CRC Press，1995.

［6］ Pan Chen，Kui Dai，Dan Wu，et al.Parallel algorithms for FIR computation mapped to ESCA architecture［C］∥Proc of 2010International Conference of Information Engineering，2010：123－126.

［7］ IEEE Standard for Binary Float－Point Arithmetic［S］.NY：The Institute of Electrical and Electronics Engineers，1985.

［8］ Qu Ying－jie，Xia Hong，Wang Qin.A research of functional testing method for microprocessor floating－point arithmetic J .Computer Engineering and Applications2001742－43.（in Chinese）

［9］ Ur S，Yadin Y.Micro architecture coverage directed generation of test programs［C］∥Proc of the 36th Design Automation Conference，1999：175－180.

附中文参考文献：

［3］ 王海霞.运算电路的形式化验证方法研究［D］.北京：中国科学院计算技术研究所，2004.

［8］ 曲英杰，夏宏，王沁.微处理器浮点去处功能的测试方法研究［J］.计算机工程与应用，2001（7）：42－43.