S型流道冷板的流体域熵产分析及流道优化

，

(哈尔滨工业大学(威海) 汽车工程学院，山东 威海 264209)

S型流道冷板的流体域熵产分析及流道优化

刘福东，谭建宇

(哈尔滨工业大学(威海) 汽车工程学院，山东 威海 264209)

粘性流体在流动和传热过程中，由于粘性耗散和热传导的存在造成能量损失。为分析流体流动和传热过程的能量损失并得到冷板的最优流道形式，本文以某电子器件用S型流道液冷冷板为分析对象，通过数值模拟，得到S型流道液冷冷板的流体域熵产率随工质流量的变化规律，对流体域充分发展的直段和弯段内熵产率大小进行了比较，并在固定流量下，分析了熵产率大小沿工质流动方向上的变化情况。提出冷板流道优化方案，并从换热表现、压头损失和总能量损失三方面对不同流道形式的冷板进行了综合评价和比较，得到了冷板流道的最优形式，为工程实际提供参考。

冷板；数值模拟；流体域；熵产；流道优化

电子器件的发展正趋向大功率和集成化，这对电子器件的热控制提出了更高的要求。液冷冷板作为一种高效成熟的热控制手段，常被用于高热流密度电子器件的冷却。液冷冷板的流道常采用S型流道，或称为蛇形流道。在设计S型流道冷板时，需综合考虑冷板工作时的换热表现、流动压降以及总能量损失。对于尺寸较小的大功率电子器件，所用冷板流道尺寸往往较小，所需的工质流量相应增大，使得工质流动的流动阻力相应增大，进而需要较大的泵功。考虑对流道的前半段进行稀疏处理，有较好换热表现的同时，可以减少内部工质流动所需的泵功。

在流动和传热的熵产分析以及换热器优化分析方面，Babaelahi M[1]等人基于熵产最小化，针对某板翅式换热器，提出了一种多目标优化方法，并通过与单一目标优化方法对比，验证了该方法的优越性；Tarlet D[2]等人通过实验，改进微型管壳式换热器结构以实现传热强化，并通过熵产理论对其进行了评价；Makinde[3]通过数值计算，得到特定的管道在变温壁面下变粘度流体熵产数的分布特点；Jeon D.H[4]对燃料电池用S型流道冷板进行了数值研究，对比四种流道下的流动和换热表现，验证了多支路流道冷板的性能优越性；柳熊斌[5]等验证了熵产极值准则在评价热功转换型换热器的热力学优化中的先进性；张荣婷[6]、翟妮娜[7]等人通过数值模拟，从流动阻力的角度对S型流道液冷冷板的流道进行了优化分析。综上，目前国内外对流动与传热的熵产分析更多的集中在基于熵产理论的评价方法创新以及对具体应用的性能评价上。

本文以某电子器件用S型流道液冷冷板为研究对象，通过熵产分析，分析其流体域内工质因粘性耗散和热传导引起的能量损失特点；提出了流道稀疏化后的冷板形式，并从换热表现、压头损失和能量损失三方面对流道稀疏后的冷板进行综合评价。

1 数学模型

1.1 熵产控制方程

对于不可压缩流体单相流动和传热过程，笛卡尔坐标系下的熵输运方程[8]表示为

(1)

式中s——熵;

u、v、w——分别表示流体微团在x、y、z方向的速度;

ρ——流体的密度;

T——流体温度;

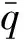
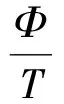
(2)

(3)

E=∫EfdV+∫ETdV

(4)

式中μ——流体的粘度;

λ——流体的导热系数。

1.2 压头损失系数

压头损失系数K的定义[6]为

(5)

式中φ——由于黏性摩擦引起的能量耗散;

um——流体平均流速。

粘性流体恒定总流的伯努利方程

(6)

对于充分发展的水平管道流动，有α1=α2=1、z1=z2、um1=um2，则有

(7)

联立式(5)和式(7)可得

(8)

1.3 努赛尔数Nu

根据努赛尔数的定义

(9)

(10)

式中h——流体与壁面间的对流换系数;

q——壁面的平均热流密度;

tw——壁面的平均温度;

tf——流体的平均温度;

d——截面的当量直径;

W——流道截面的宽度;

H——流道截面的深度。

2 物理模型

2.1 物理描述

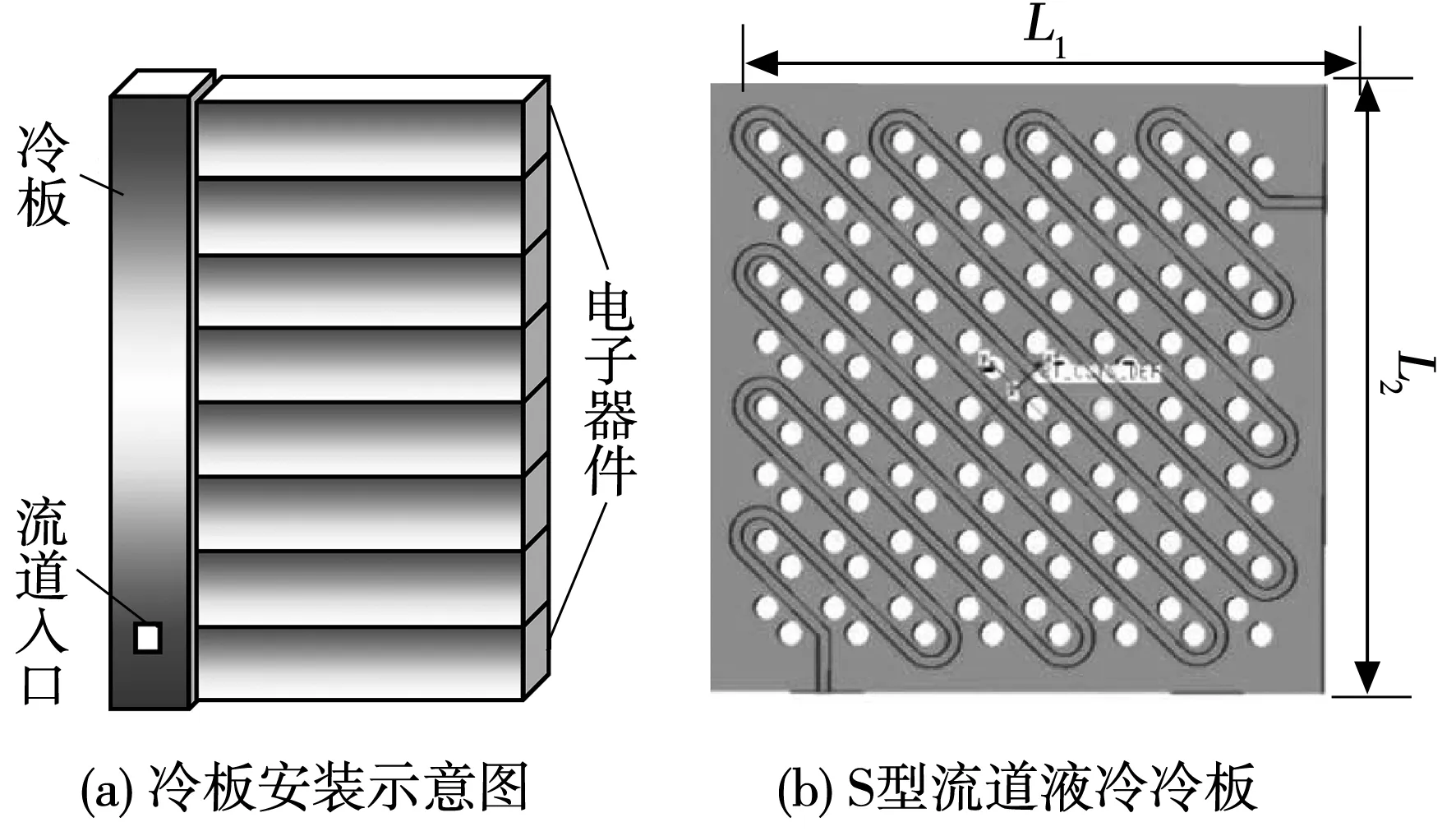
图1 S型流道液冷冷板模型

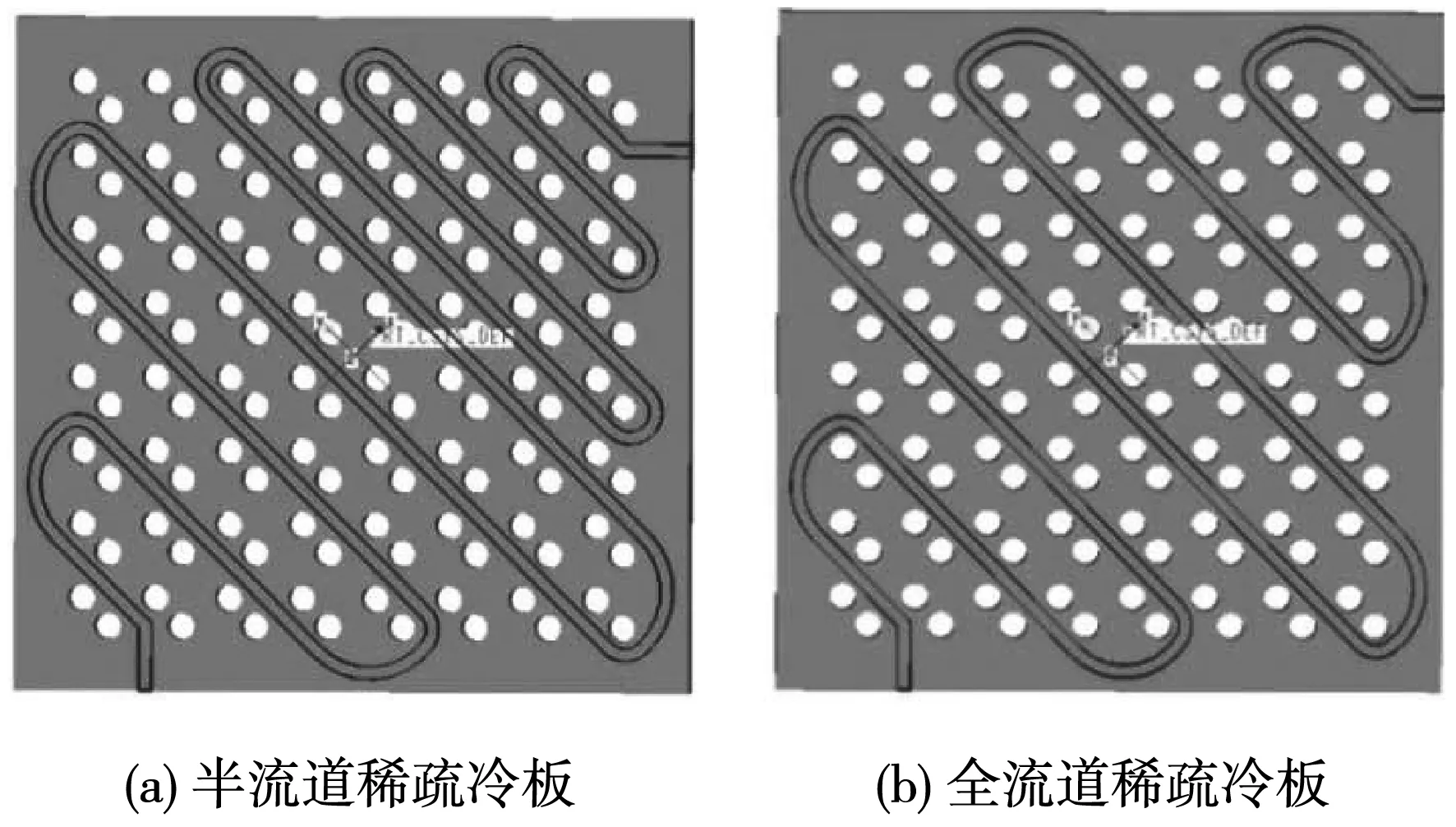
图2 流道稀疏处理后的冷板

某电子器件的S型流道液冷冷板三维几何模型如图1所示，冷板的侧面与电子器件箱接触，电子器件箱内包含发热元件。冷板长L1为65 mm，宽L2为75 mm，厚度为6 mm，材质为金属铝；冷板上包含端子通孔，设计的流道绕开端子通孔，流道截面尺寸(宽×高)为1.5 mm×2 mm，截面距冷板上下面各2 mm；另外根据流道特点提出两种流道稀疏化后的冷板优化模型，图2a为对流道前半段稀疏化处理的冷板，图2b为整条流道稀疏化处理的冷板。

2.2 计算方法与边界条件

本文采用有限体积法对冷板进行流动和传热的熵产分析、流动阻力分析及传热分析，选择的湍流模型为标准k-ε模型，近壁面选择标准壁面函数法。

边界条件设置：选择液体工质为水，冷板流道入口为质量流量入口，入口水温为303 K；流道出口选择为压力出口；冷板底面施加固定热流边界条件，热流密度为50 000 W/m2，冷板的其他面为绝热边界条件。

对流体域边界处网格进行加密，并采用非结构化网格。通过网格无关性验证，发现最大网格尺寸为0.25 mm时，有较好的收敛结果和较高的计算精度。

3 冷板内流体域的熵产分析

3.1 流体域总熵产随工质流量的变化

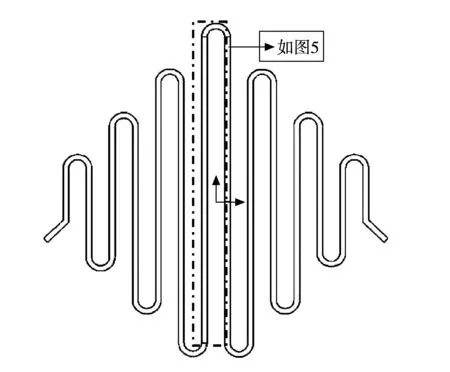
图3 S型流道冷板的流体域示意图

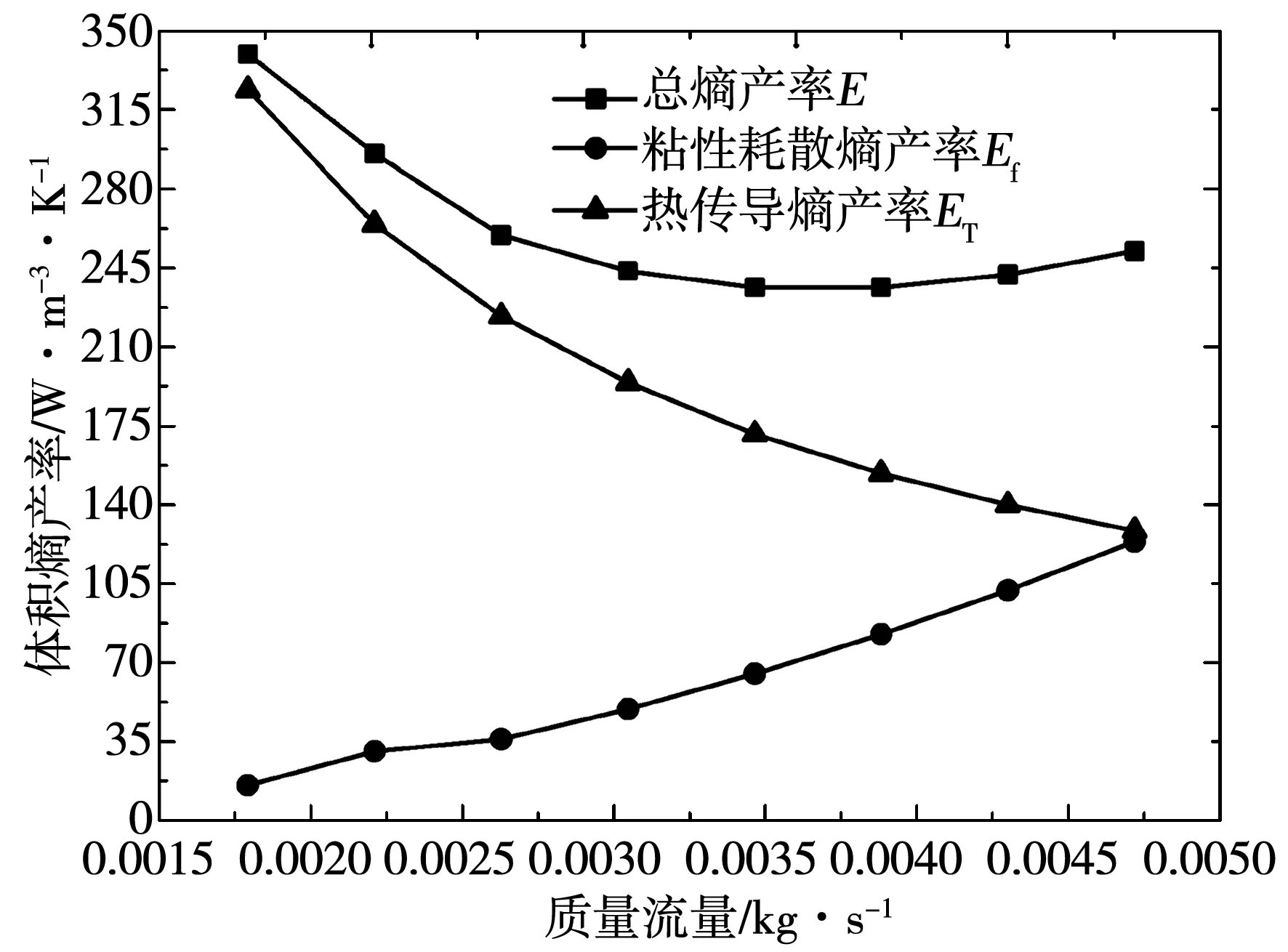
图4 流体域内熵产率随工质流量的变化

S型流道冷板的流体域如图3，由数值模拟得到整个流体域的熵产率随流量变化情况，如图4，可以看出，在研究的工质流量范围内，热传导引起的熵产ET要大于黏性耗散引起的熵产Ef；且随着水量的增加，Ef逐渐增大而ET逐渐减小，使得流体域的总熵产率呈现出先减小后增大的趋势，在工质流量为0.003 5 kg/s左右总熵产率E存在最小值。

3.2 流体域中直段和弯段的熵产率

取整个流体域中已充分发展的一直段和一半圆弯段进行熵产率分析，分析区域如图5，直段长度为0.086 3 m，半圆弯段半径为0.003 1 m。

由计算结果得到直段和弯段的熵产率随流量的变化，如图6，粘性耗散引起的熵产方面，相同流量下弯段的数值大于直段，这说明弯段内粘性耗散相较直段更剧烈；而在热传导引起的熵产方面，相同流量下直段的数值大于弯段，说明直段内温度梯度更大；而在总熵产方面，直段和弯段的总熵产率都呈现出先减小后增大的趋势，流量小于0.003 5 kg/s时，直段内总熵产大于弯段内总熵产，流量大于0.003 5 kg/s时，弯段内总熵产大于直段内总熵产。

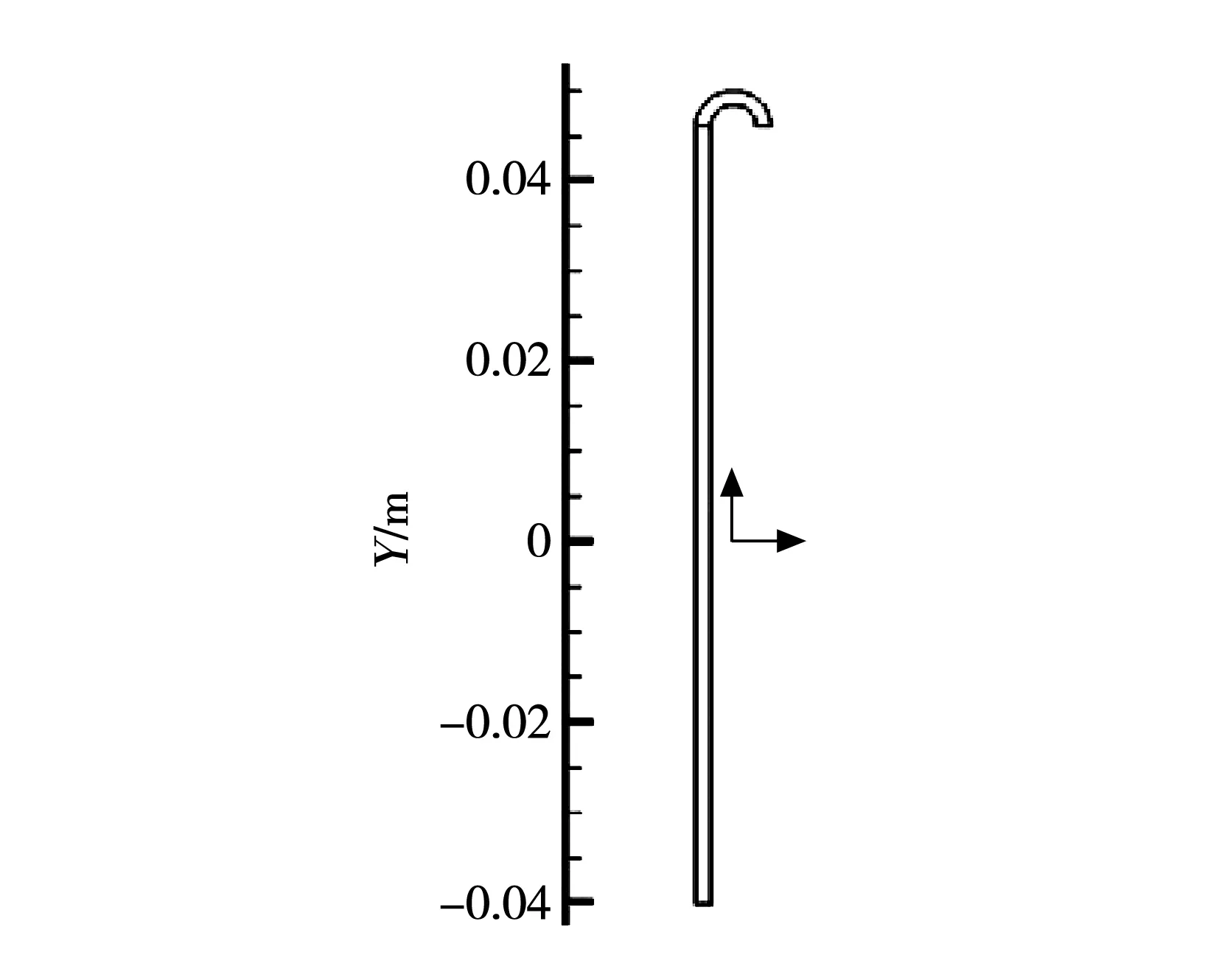
图5 流体域中的直段和弯段示意图

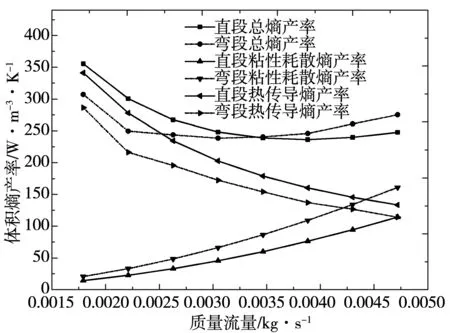
图6 流体域直段和弯段内熵产率随流量的变化

3.3 熵产率沿工质流动方向的变化

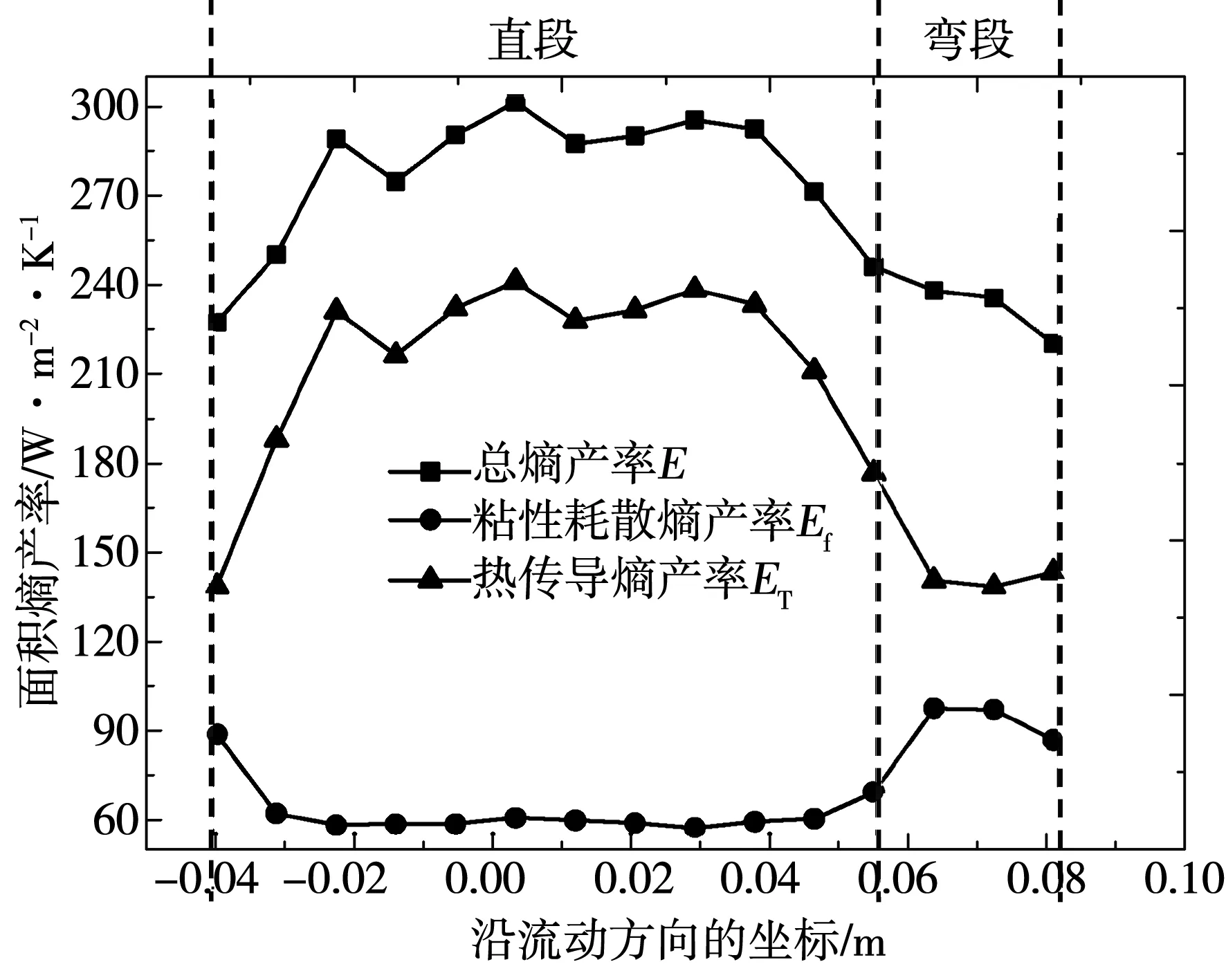
图7 熵产率沿工质流动方向的变化

将图5所示流体域沿流动方向上取15个等距截面，分析工质流量为0.003 5 kg/s时熵产率沿工质流动方向的变化情况，如图7。可以看出，同一截面上由热传导引起的熵产ET远大于粘性耗散引起的熵产Ef；从ET的变化曲线可以看出，在直段上沿流动方向先增大后趋于平稳，并在半圆段的第一个截面开始逐渐减小，在弯段的最后一个截面，减小到最小值；Ef在直段上沿流动方向熵产率先减小后趋于平稳，并在半圆段的第一个截面开始逐渐升高，在弯段的中心截面上增大到最大值；总熵产方面，整体上呈现出先增大后趋于稳定然后减小的趋势，并在弯道的出口处达到最小值。

由熵产率沿流动方向的变化规律，可以看出，Ef较大的区域，ET往往较小，而Ef较小的区域，ET较大。由熵产计算公式可知，速度梯度和温度梯度的大小直接决定了熵产率的大小，熵产变化之所以有图7所示的规律，在于壁面受流体冲刷剧烈的区域，速度梯度较大而温度梯度较小，反之，速度梯度较小而温度梯度较大，造成熵产率沿工质流动方向的变化。

4 冷板流道的优化分析

在相同工况下，分别对常规S型流道液冷冷板、半流道稀疏冷板和全流道稀疏冷板进行内部流体的流动和传热分析，三种流道形式下的冷板如图1和图2所示，通过不同流道形式冷板的努赛尔数及冷板底面温度分布、总压头损失系数以及总熵产的对比，对冷板的性能做出综合评价。

4.1 不同流道冷板的换热效果比较

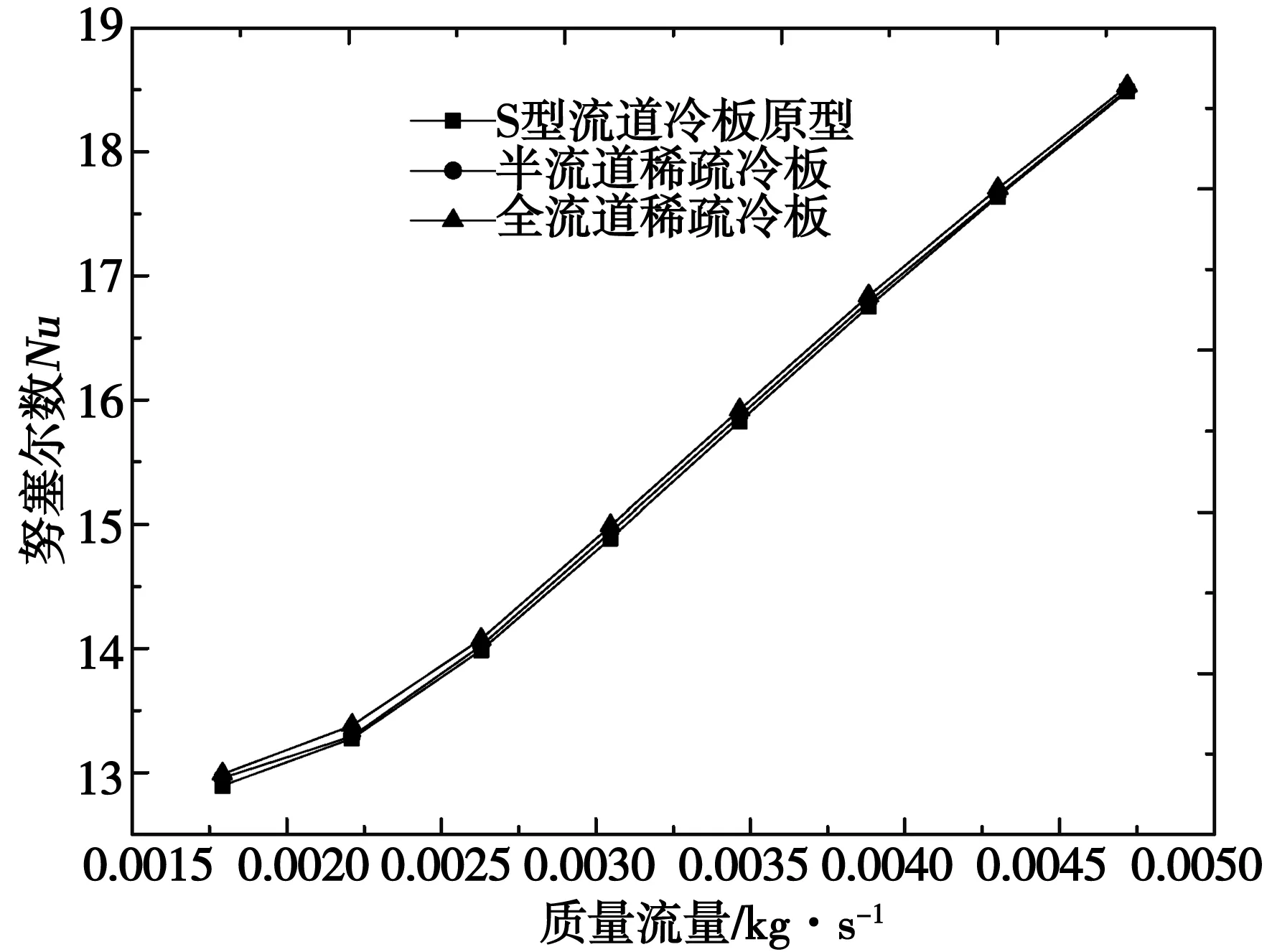
图8 三种冷板内流体对流换热的Nu数随流量的变化

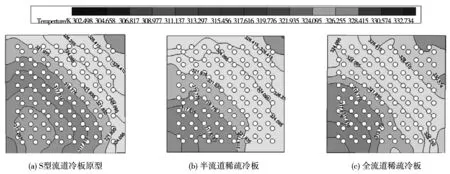
图9 工质流量为0.003 5 kg/s时三种冷板的底面温度分布(K)

图8为相同工况下不同冷板内部流体与流道壁面对流换热的努赛尔数随流量的变化情况，可以看出，Nu随流量的增加而增大，但相同流量下三种流道形式对应的Nu相差不大，这说明流道稀疏化对冷板内的流体与流道壁面的对流换热强度影响不大。

另外，得到三种流道形式的冷板在相同热工况下的底面温度分布，以流量为0.003 5 kg/s时的冷板底面温度分布为例，如图9，全稀疏流道形式的冷板高温区域较大，不满足换热要求，后续的性能评价可排除此方案；S型流道冷板原型和半稀疏流道冷板的底面温度差异体现在流道的前半段，前者的前半段温度较低，而两者在流道后半段差别不大且高温区域的大小几乎相同，均能较好的满足电子器件的散热要求。

4.2 不同流道冷板的压头损失对比

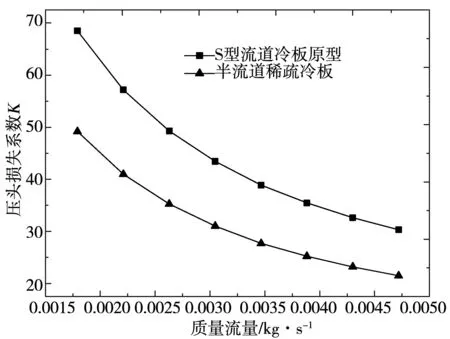
图10 两种冷板总压头损失系数随流量的变化

冷板压头损失系数的大小反映了对泵功的要求，工程实际中，流量不变的前提下，压头损失系数越大，所需的泵功也越大。对于冷却效果接近的两种冷板，图10给出了在相同工况下压头损失系数随流量的变化情况。可知，总压头损失系数随流量的增加而减小，但减小的幅度越来越小；在相同流量下，S型流道液冷冷板原型的总压头损失系数数值上远大于半流道稀疏冷板的压头损失系数，需要更大的泵功。

4.3 不同流道冷板的总熵产随工质流量的变化

图11 三种流道形式的冷板总熵产随流量的变化

冷板工作时的总熵产包括三部分：流体域中粘性耗散引起的熵产、流体域中热传导引起的熵产以及固体域中热传导引起的熵产。通过数值计算得到S型流道冷板原型和半流道稀疏冷板的总熵产随工质流量的变化，如图11，可以看出，两种流道形式下冷板的总熵产随着工质流量的增大而减小，其原因在于：随着工质流量的增加，虽然流体域内粘性耗散引起的熵产在不断增大，但是由流体域和固体域内热传导引起熵产在不断减小，造成总熵产在数值上逐渐减小。

此外，在工质流量较小时，S型流道冷板原型的总熵产要大于半流道稀疏冷板，但流量增加至约0.003 2 kg/s后，S型流道冷板原型的总熵产小于半流道稀疏冷板的总熵产。

综上，对比三种流道形式冷板的换热效果，发现全流道稀疏冷板底面高温区域过大而不满足要求；而对于满足换热要求且冷却效果接近的S型流道冷板原型和半流道稀疏冷板，在相同流量下，半流道稀疏冷板具有更小的压头损失，在工程实际中所需的泵功也较少，而在总熵产方面，在所研究的流量范围内，两种冷板互有大小且相差不大。所以，本文选择半流道稀疏冷板作为流道优化的方案。

5 结论

本文对某电子器件用S型流道液冷冷板的流体域进行了熵产分析，包括熵产率随流量的变化、沿工质流动方向的熵产率变化以及流体域弯段和直段内熵产率的对比；对S型流道液冷冷板提出流道优化方案，并通过换热表现、压头损失以及总熵产的综合比较，验证了优化方案的性能优越性，结果如下：

(1)S型流道液冷冷板流体域的总熵产随工质流量增加先减小后增大，且熵产最小时对应的工质流量为 0.003 5 kg/s。由黏性耗散引起的熵产随流量的增加而增大，由热传导引起的熵产随流量增加而减小。

(2)同一流量下，相比于直段，弯段内粘性耗散引起的熵产率更大，热传导引起的熵产率更小；流量为0.003 5 kg/s时，在流体域的某一直段和弯段内，沿流动方向上的熵产率呈现出先增大后趋于稳定，然后减小的趋势。

(3)对流道前半段进行稀疏化处理后的S型流道冷板，兼具了较好的换热表现以及更小的压头损失。

[1]Babaelahi M, Sadri S. Multi-Objective Optimization of a Cross-Flow Plate Heat Exchanger Using Entropy Generation Minimization[J].Chemical Engineering & Technology,2014,37(1):87-94.

[2]Tarlet D, Fan Y, Roux S, et al. Entropy generation analysis of a mini heat exchanger for heat transfer intensification[J].Experimental Thermal and Fluid Science,2014(53):119-126.

[3]Makinde O.D. Entropy-generation analysis for variable viscosity channel flow with non-uniform wall temperature[J].Applied Energy,2008,85(5):384-393.

[4]Jeon D. H. Numerical study of serpentine flow-field cooling plates on PEM fuel cells performance[J].International Journal of Energy Research,2013,6(37):510-521.

[5]柳雄斌,孟继安,过增元.换热器参数优化中的熵产极值和热动耗散极值[J].科学通报,2008,53(24):3026-3029.

[6]张荣婷,余小玲,冯全科.电力电子集成模块用冷板中液流通道结构优化及传热数值分析[J].电子器件,2008,31(5):1618-1622.

[7]翟妮娜.S型流道液冷冷板性能分析与结构优化[D].西安:西安电子科技大学,2013.

[8]Herwig H, Kock F. Local entropy production in turbulent shear flows: A tool for evaluating heat transfer performance[J].Journal of Thermal Science,2006,15(2):159-167.

[9]Makhanlall D, Liu L H, Zhang H C. Determination of loss coefficients for high-temperature flow devices: An entropy-based approach[J].International Journal of Thermal Sciences,2010,49(9):1848-1855.

Entropy-generationAnalysisandFlowOptimazationfortheCooling-platewithaSerpentineFlowChannel

LIU Fu-dong, TAN Jian-yu

(School of Harbin Institute of Technology, Weihai 264209, China)

Energy loss occurs in the process of flow and heat transfer with the viscous fluid. To analyze the energy loss and get the optimal flow channel of the cooling-plate, we have got entropy-generation rate which is variable with the working medium flow in the fluid domain of the cooling-plate with serpentine flow channel by numerical simulation. Results show the minimum flow rate for the least entropy generation. Besides, the entropy generation generating in the straight section is contrasted with the entropy generation in the curved section of the flow channel. In addition, the variation of the entropy generation along the flow direction have been analyzed in a constant flow rate. Then three projects are compared to get the best flow channel with a comprehensive evaluation which includes the heat transfer performance, head loss and energy loss, and can provide reference for the engineering practice.

cooling-plate; numerical simulation; the Fluid domain; entropy generation; optimization of channel

2014-05-21修订稿日期2014-06-19

教育部新世纪人才支持计划(NCET-12-0152)

刘福东(1989～)，男，硕士研究生，研究方向为航天器热控制。

TK124

A

1002-6339 (2014) 05-0392-05