压电组件嵌入式风洞模型支撑系统振动主动控制仿真

聂旭涛，陈万华，陈振华，王元兴

(1.空气动力学国家重点实验室，四川 绵阳 621000；2.中国空气动力研究与发展中心，四川 绵阳 621000)

风洞试验通常采用尾部支撑方式，试验模型通过内置天平、尾支杆与弯刀支板相连，弯刀支板固定在试验段后部，由此构成的风洞模型支撑系统为一典型的悬臂式结构系统。吹风试验时，受非定常流气场作用，模型支撑系统会产生不同程度振动，严重时直接影响试验数据测量的准确性。而且，若振动时间过长、幅度过大、频率过高，可能损坏系统结构，威胁风洞试验安全[1]。

为保证风洞试验时试验模型不会产生不可接受的振动，必须对风洞模型支撑系统进行结构振动控制。结构振动控制分为被动、半主动和主动振动控制三类。其中，振动主动控制不需改变系统的主体结构，只在结构局部安装驱动元件，如压电组件、电磁质量块等，根据外部激励实时调整反向控制力，达到降低结构振动的目的。目前，振动主动控制技术已在西方发达国家得到广泛研究与成功应用[2]。NASA Langley 研究中心的Robert在F/A-18缩比模型垂尾布置压电作动器，使其根部应变均方根减小50%[3]；德国ERAS公司采用压电陶瓷材料研制主动抑振系统(Active Anti-Vibration System，AVS),有效降低了欧洲跨声速风洞(European Transonic Wind Tunnel，ETW)试验模型的振动[4]。在国内，振动主动控制技术研究起步较晚、应用差距较大，特别是在风洞工程领域方面。陈卫东等人基于电磁激励质量块原理开展跨声速风洞模型支撑系统主动振动控制研究，目前还处于地面调试和优化阶段[5]。为此，本文基于国内振动主动控制发展现状及实际工程迫切需求，对基于压电组件风洞模型支撑系统振动主动控制仿真技术展开研究，主要包括压电智能材料机电耦合行为、压电组件嵌入式模型支撑系统、系统主动振动控制仿真、嵌入式结构强度分析等内容。

1 压电智能材料机电耦合行为

基于压电智能材料进行被控对象的主动振动控制，实质上就是利用压电材料的正逆压电效应，通常可由以下压电方程所表征：

(1)

式中:ε为应变；cE为电场强度为零(或常数)时弹性柔顺常数；d为压电常数，是应力恒定时电场强度引起应变变化与电场强度变化之比；D为电位移；εσ为应力为零(或为常数)时的介电常数；σ为应力；E为电场强度。

若不对称结构晶体材料在一定方向上受到机械力，则两个端面出现符号相反的束缚电荷，即正压电效应；若不对称结构晶体材料受到电场作用，则产生与电场强度成比例的机械力，即逆压电效应。

根据风洞模型支撑系统的结构特点，采用多层式陶瓷驱动器作为主动振动控制驱动元件。多层式陶瓷驱动器由多层单片陶瓷叠加而成，能够累积各个陶瓷片的变形，具有承载力大、响应快、位移重复性好、电场控制相对简单等优点。

根据压电方程(1)，多层式陶瓷驱动器电压、驱动力和位移三个参数之间有如下关系：电压恒定情况下，驱动力为零时变形最大；反之，变形为零时，驱动力最大。实际仿真建模时，压电组件等效模拟为弹簧元件。

2 压电组件嵌入式模型支撑系统

风洞模型支撑系统由试验模型、尾支杆、弯刀支臂和弯刀组成，见图1。弯刀在弯刀支座内滑动，以形成不同的攻角试验状态。鉴于弯刀支座刚性相对较强，对系统振动影响不大，文中系统模型未计入该部件。

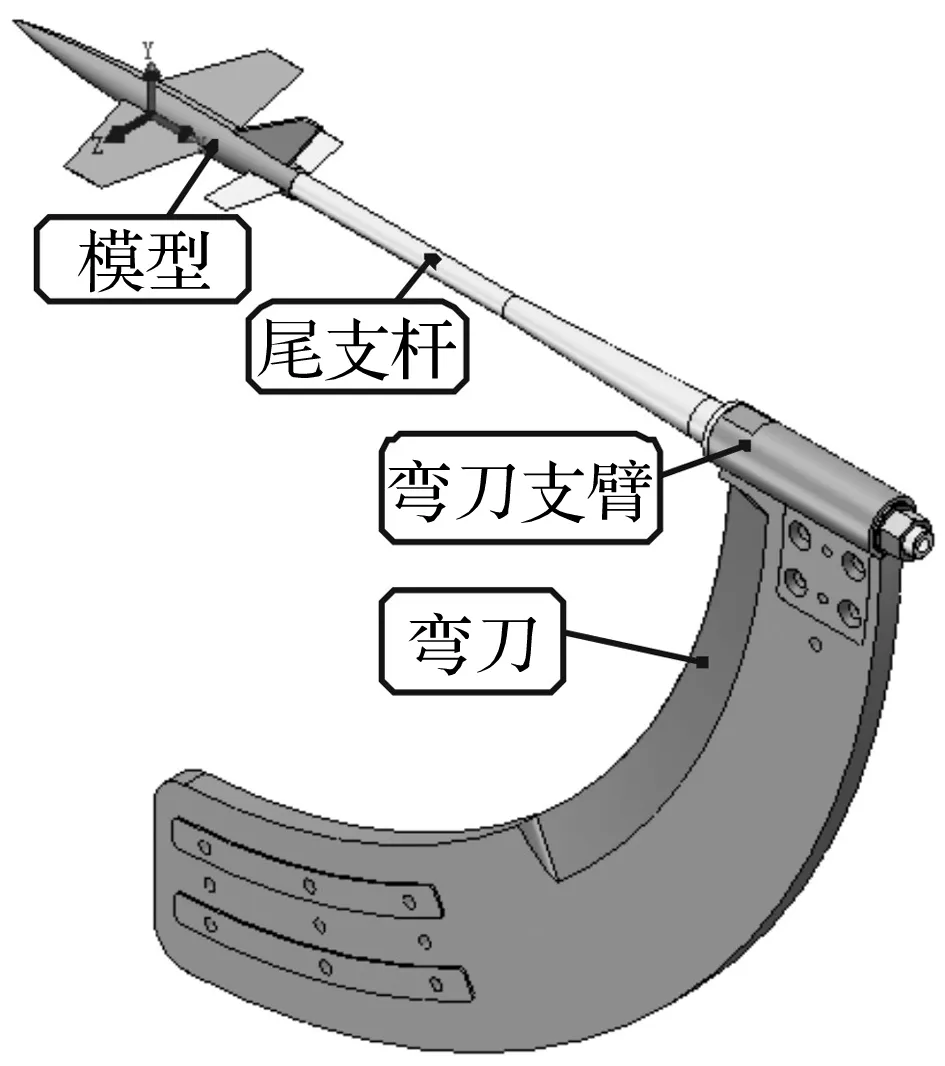
图1 模型支撑系统组成

图2 模型支撑系统结构模态

采用MSC.PATRAN/NASTRAN有限元软件对模型支撑系统进行结构模态分析，提取前二阶振型结果，见图2,一阶模态频率约为28 Hz，振型为横向摆动；二阶模态频率约为31 Hz，振型为俯仰摆动。

文中对模型支撑系统第2阶模态进行振动控制研究，即控制其在俯仰方向上的振动。基于压电组件振动主动控制的原理是，根据实时气动载荷情况，对压电组件施加相应的控制电压，产生驱动尾支杆的作用力，以形成与气动载荷作用相反的弯曲力矩，达到降低结构振动幅值的目的。依据上述原理，修改原模型支撑系统的尾支杆结构，即在尾支杆尾部将其分为前、后两段，并将两组压电组件装入两分段之间，从而组成压电组件嵌入式模型支撑系统。图3部分显示了压电组件嵌入式尾支杆结构。

图3 压电组件嵌入式尾支杆结构

3 压电组件关键性能参数分析

驱动力是压电组件最为关键的性能参数之一。为降低结构振动，压电组件驱动力驱动模型中心在俯仰方向的位移应该与气动载荷在此处引起的俯仰方向位移大致相当，方向相反。这里，基于尾支杆结构的频率响应函数矩阵来确定压电组件驱动力。

尾支杆结构动力学方程为

(2)

式中:[M]为质量矩阵；[C]为阻尼矩阵；[K]为刚度矩阵；{f}为外部载荷向量；{x}为结构响应向量。

将上式拉氏变换(变量jω)，可得：

(p2[M]+p[C]+[K]){X(jω)}={F(jω)}

(3)

计算方程式(3)的系统特征方程得到特征值λr及其对应的特征向量{Ψ}r，得到系统传递函数为

[H(jω)]=

(4)

式中:Qr=PrRr，其中Pr为与特征值有关常数，Rr为与特征向量换算比例有关常数。

频率响应函数矩阵[H(jω)]把频率函数的系统输出位移{X(jω)}和输入力{F(jω)}关联起来，即

{X(jω)}=[H(jω)]{F(jω)}

(5)

根据上式，分别在模型中心施加气动载荷和在压电组件驱动位置施加驱动力，计算对应于模型中心在俯仰方向上自由度的频率响应函数，通过比较可初步确定压电组件所需驱动力值。

MSC.PATRAN环境下创建尾支杆结构有限元模型，见图4。模型中心处创建点单元，且赋予质量属性；模型中心与尾支杆前端面、压电组件驱动点与其驱动面分别创建MPC单元。

图4 尾支杆结构有限元模型

基于图4中有限元模型，运用MSC.NASTRAN计算尾支杆结构的频率响应函数矩阵，分别获得气动载荷与压电组件驱动对模型中心俯仰方向位移自由度的频率响应函数曲线，见图5(a)、(b)。两个曲线均在频率约31Hz处出现峰值，峰值之比约为460。根据实测气动载荷幅值，初步确定压电组件所需最大驱动力值为2.8 kN。考虑到压电组件驱动力会随驱动位移下降，选择标称推力为4 kN的压电组件，对应的标称位移为20 μm。

图5 尾支杆频率响应函数曲线

4 模型支撑系统振动仿真

风洞模型支撑系统中，相对于弯刀等零部件，尾支杆结构刚度较弱，可视为柔性体，其余零部件则视为刚性体。所以，文中基于刚柔耦合动力学理论建立模型支撑系统振动仿真模型。

刚柔耦合多体系统中，刚体按多刚体系统动力学理论建立方程；柔性体则用离散化的若干个单元的有限节点自由度来表示物体的无限多个自由度。这些单元节点的弹性变形近似地用少量模态的线性组合来表示[6]。

根据系统外力和总能量分析，运用拉格朗日乘子法建立刚柔耦合动力学方程

(6)

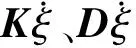
依据刚柔耦合动力学理论，联合MSC.ADAMS和MSC.PATRAN/NASTRAN软件，建立模型支撑系统的振动仿真模型[7]：

(1)MSC.PATRAN环境下创建尾支杆柔性体模型，包括划分网格、定义连接点及其MPC单元、定义单元材料属性等。

(2)运用MSC.NASTAN计算生成尾支杆柔性体中性文件。

(3)ADAMS/View环境下，导入尾支杆柔性体模型；导入模型支撑系统其它零部件，如模型、弯刀、弯刀支臂等，均视为刚体；根据所选压电组件刚度参数创建两件弹簧用于模拟压电组件；根据部件间联接关系创建运动约束副。创建后的模型支撑系统振动仿真模型如图6所示。

图6 模型支撑系统振动仿真模型

模型中心处施加Y向正弦激励，同时将模拟压电组件的弹簧单元失效。设置仿真求解器参数，计算获得未施加控制时飞机模型强迫振动结果。图7为模型中心Y向位移随时间变化曲线，幅值约为0.34 mm。

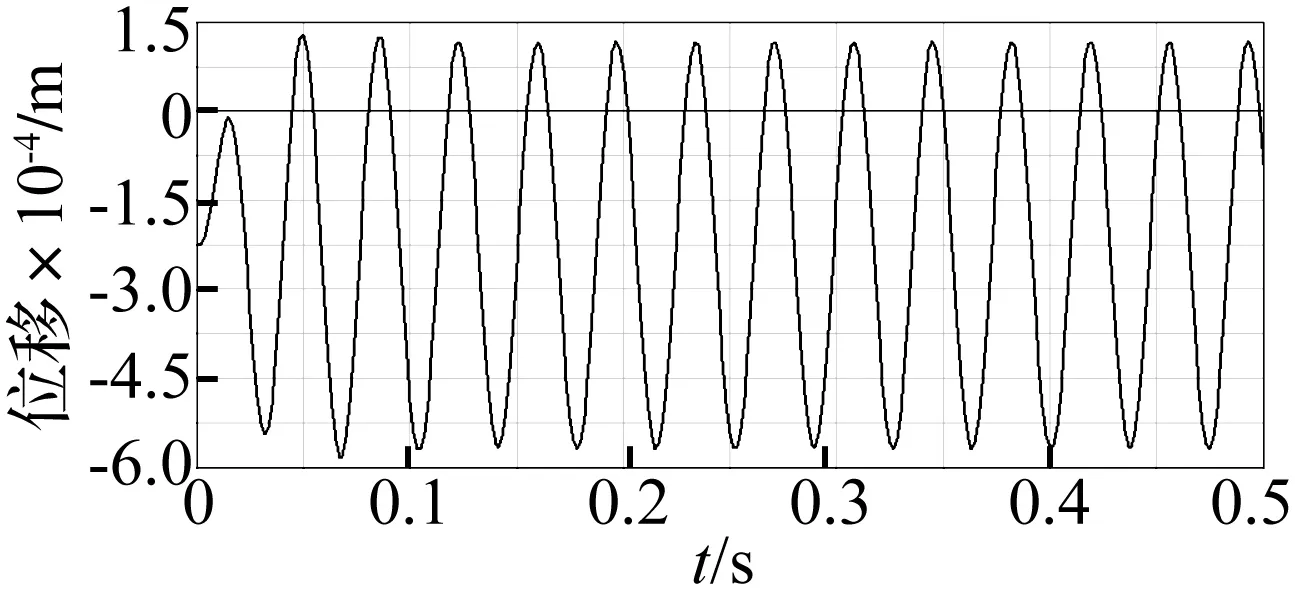
图7 模型支撑系统振动仿真结果

5 模型支撑系统振动主动控制仿真

目前，振动主动控制算法主要有PID控制算法，二次型线性最优控制算法、神经网络控制算法、模糊控制算法等。本文选用经典PID控制算法，原理简单，易于实现，具有较强的鲁棒性和可靠性。

PID控制是一种线性控制方法，根据给定值r(t)与实际输出值y(t)构成控制偏差e(t)，即e(t)=r(t)-y(t)。对偏差e(t)进行比例 、积分和微分运算，将三种运算结果相加，就得到PID控制器的控制输出u(t)。

在数字控制系统中，根据采样时刻的偏差值计算控制量，PID控制器中的积分和微分项需要进行离散化处理。以一系列的采样时刻点kTs代表连续时间t，以求和代替积分，以增量代替微分，得到离散的PID表达式：

(7)

式中:u(k)为第k次采样时刻控制器的输出值，kp为比例系数，ki为积分系数，kd为微分系数，Ti为积分时间常数，Td为微分时间常数，Ts为采样周期。

文中采用ADAMS/Controls模块实现PID控制器。ADAMS/Controls模块能够将机械系统仿真与控制设计仿真有机连接起来，实现结构控制一体化仿真[8]。控制设计仿真部分采用MATLAB软件Simulink工具箱，编写整个系统的控制图，而将ADAMS/View的机械系统样机模型设置为控制图中的一个模块，相互传递状态变量进行信息交流。

图8(a)显示了ADAMS/Control模块创建的风洞模型支撑系统振动仿真模块：设定模型支撑系统振动仿真模型的输出状态变量为飞机模型中心Y向位移，输入状态变量为飞机模型中心处气动载荷以及两处压电组件的驱动力。因此，气动载荷作用下飞机模型中心在Y向产生位移，Matlab/Simulink控制程序根据此实时位移，基于经典PID算法计算压电组件需要产生的控制力，输入到ADAMS振动仿真模型以平衡气动载荷，减小振动幅值。基于该振动仿真模块，Matlab/Simulink环境下构造控制系统方框图，如图8(b)所示。

设定正弦激励作为飞机模型中心处气动载荷，输入至系统振动仿真模块；经模块内ADAMS/Solver求解，获得飞机模型中心Y向位移值，作为系统振动仿真模块输出状态变量；与期望值比较后获得偏差，经PID控制算法模块计算，获得两组压电组件驱动控制力，并输入至系统振动仿真模块。确定PID参数，设置Matlab/Simulink求解器参数，执行计算，获得主动振动控制仿真结果。

图9显示了控制后模型中心Y向位移随时间变化曲线，振幅为0.13 mm，相对于控制前降低了约62%，减振效果明显。

图8 模型支撑系统振动主动控制仿真模型

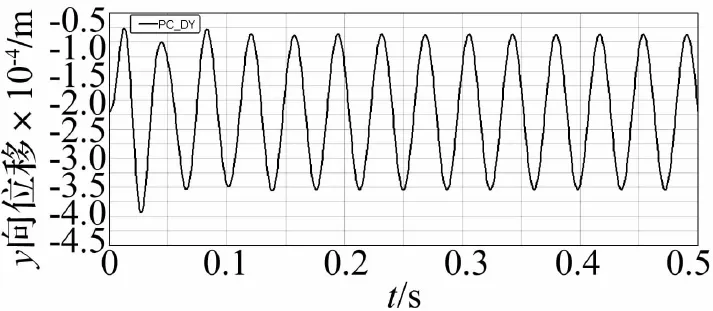
图9 控制后模型中心Y向位移曲线

图10 压电组件驱动力曲线

图10(a)和图10(b)分别显示了上下两件压电组件驱动力随时间变化曲线，驱动力峰值约为2.7 kN，没超过压电组件标称推力4 kN。

图11(a)和图11(b)分别显示了上下两件压电组件驱动位移随时间变化曲线，驱动位移峰值约为9 μm，没有超过压电组件标称行程20 μm。

图11 压电组件驱动位移曲线

6 嵌入式结构强度分析及优化

风洞模型支撑系统主动振动控制模型未考虑压电组件嵌入处的非线性接触环节，本质上是一类线性仿真模型，具有较高的计算效率，以满足于计算复杂、迭代频繁的结构控制一体化仿真。但是，为了确保实际系统结构能够安全可靠运行，必须对压电组件嵌入处的接触应力进行强度校核。本文基于前节气动载荷以及压电驱动力，采用ABAQUS非线性有限元分析软件，计及接触非线性环节，建立压电组件嵌入式结构有限元模型，如图12所示，主要包括试验模型、尾支杆前段、尾支杆后段、2件压电组件和4件螺钉。压电组件固定于尾支杆后段，尾支杆后段插入尾支杆前段，并通过螺钉紧固相联，同时压电组件球头紧顶尾支杆前段接触平面。

图12 压电组件嵌入式结构有限元模型

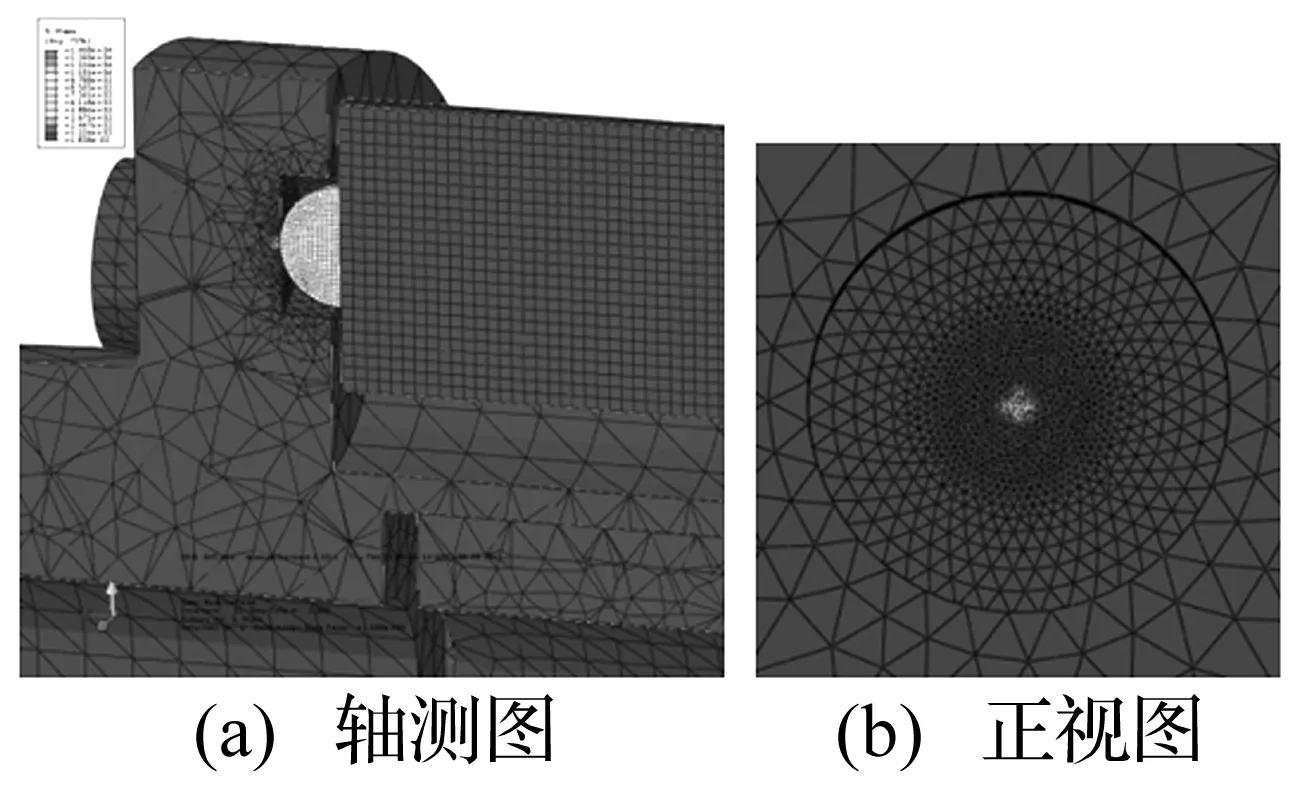
图13 接触应力分布

依据结构特点，建立各个部件之间的接触约束关系。创建非线性分析载荷步，设置边界条件与求解参数，计算获得结构变形及强度分布结果。图13显示了压电组件嵌入处接触应力，约14 680 MPa，远远超过材料抗压强度。实际工作中，前段尾支杆与压电组件球头接触处会出现材料破裂，形成小坑，影响振动控制效果。

造成过大接触应力的原因是，压电组件球头与前段尾支杆之间为点接触，接触面积很小，接触压强极大。为此，根据压电组件球头尺寸修改尾支杆前段接触平面为一球面，增大接触面积，如图14。

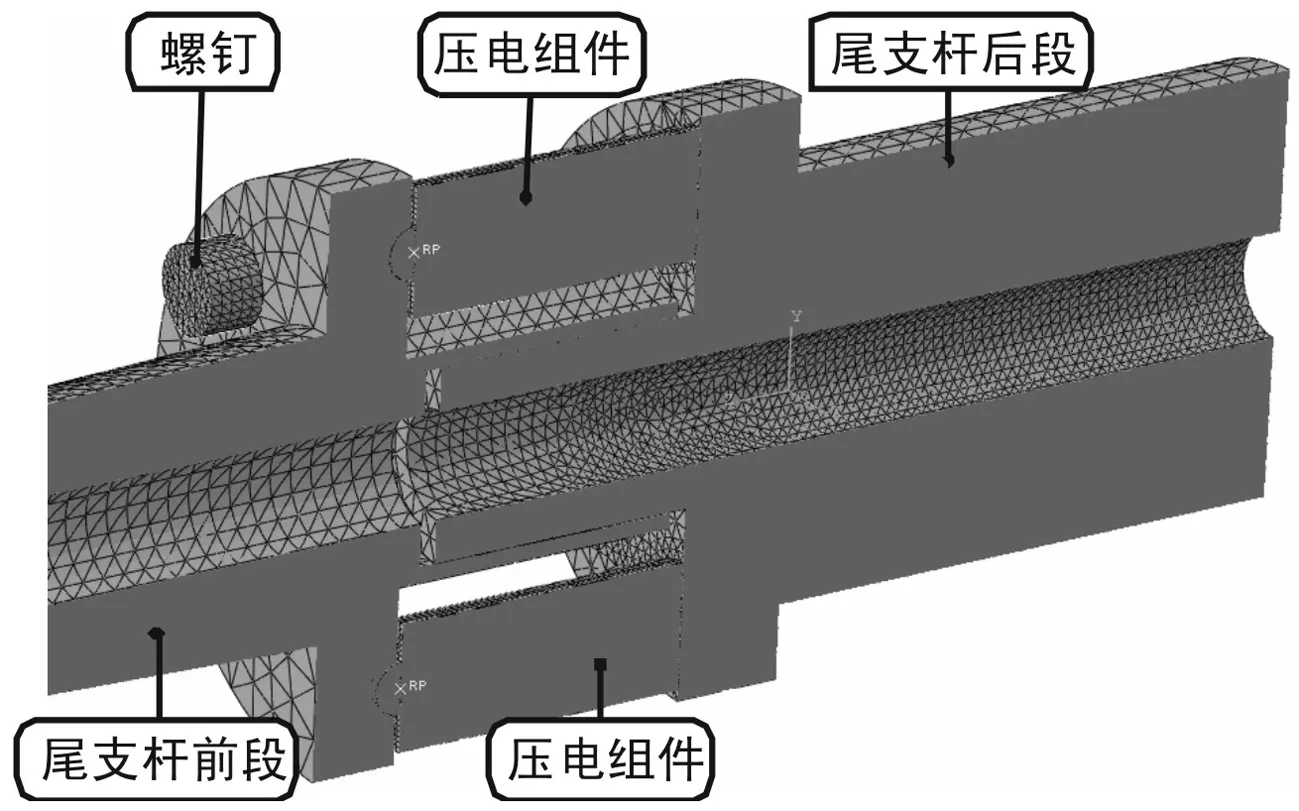
图14 修改后压电组件嵌入式结构

边界条件与求解参数不变，计算获得结构变形及强度分布结果。图15显示了压电组件嵌入处接触应力，约245 MPa，能够满足材料强度设计要求。

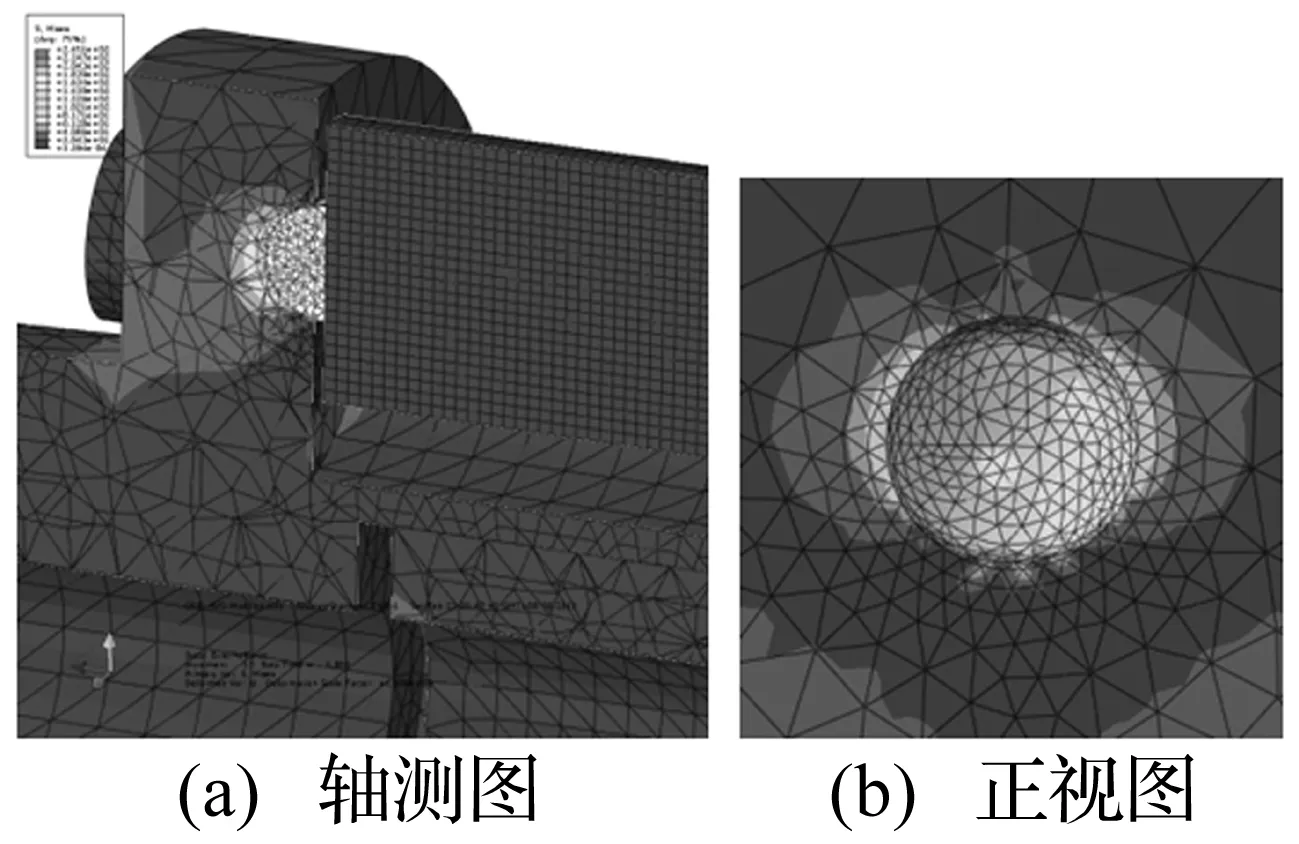
图15 修改后接触应力分布

7 结 论

本文基于压电陶瓷力学特性、刚柔耦合动力学理论、PID控制、频率响应函数矩阵等多种理论，运用MSC.PATRAN/NASTRAN、MSC.ADAMS、Matlab/Simulink、ABAQUS等多种仿真计算软件，设计了压电组件嵌入式风洞模型支撑系统，实现了模型支撑系统振动主动控制仿真，优化了压电组件嵌入结构型式。通过比较控制前后的风洞模型支撑系统动力学仿真结果，表明文中建立的结构控制一体化仿真模型，能够为实现风洞模型支撑系统有效减振、相关压电产品选型提供可靠的理论依据；通过计及接触环节的非线性有限元分析，表明文中优化后的压电组件嵌入结构型式安全可靠，同时为实现多个自由度方向减振提供了可能，具有良好的工程应用价值。

[1]Young C P，Popernack T G，Gloss B B.National transonic facility model and model support vibration problems[R].AIAA Paper，1990，90-1416.

[2]欧进萍.结构振动控制-主动、半主动和智能控制[M].北京:科学出版社，2003.

[3]Moses R W.Active vertical tail buffeting alleviation on an F/A-18 model in a wind tunnel[C].NASA Conference Publication，NASA，1999: 821-830.

[4]Fehren H，Gnauert U，Wimmel R.Validation testing with the active damping system in the European Transonic Wind Tunnel[R].AIAA Paper，2001，01-0610.

[5]陈卫东，邵敏强，杨兴华,等.跨声速风洞测力模型主动减振系统的试验研究[J].振动工程学报,2007,20(1):91-96.

CHEN Wei-dong，SHAO Min-qiang，YANG Xing-hua，et al.Experimental evaluation of an active vibration control system for wind tunnel aerodynamic models[J].Journal of Vibration Engineering，2007，20(1):91-96.

[6]Andreas H，Martin A，Ondrej V.Modal multifield approach for an extended flexible body description in multibody dynamics[J].Multibody System Dynamics，2005，13(3): 299-322.

[7]聂旭涛,赖欢,张艳辉.半柔壁喷管机构动力学仿真技术研究[J].实验流体力学，2012，26(4): 91-95.

NIE Xu-tao，LAI Huan，ZHANG Yan-hui.Simulation technique of semi-flexible nozzle machine dynamics[J].Journal of Experiments in Fluid Mechanics，2012，26(4):91-95.

[8]杨英,刘刚,赵广耀.基于ADAMS机械模型的车辆主动悬架控制策略与仿真[J].东北大学学报(自然科学版)，2006，27(1): 72-75.

YANG Ying，LIU Gang，ZHAO Guang-yao.Control strategy based on ADAMS mechanical model for’ vehicle s active suspension and simulation [J].Journal of Northeastern University(Natural Science)，2006，27(1):72-75.