故障特征选择与特征信息融合的加权KPCA方法研究

张 恒，赵荣珍

(1.兰州理工大学 数字制造技术与应用省部共建教育部重点实验室，兰州 730050;2.兰州理工大学 机电工程学院，兰州 730050)

在机械装备信息化技术发展中，机械运行状态的量化特征描述，已成为关乎该项技术是否能够科学发展的关键性问题。为此，建立起一种能够科学描述机械装备运行状态的量化特征模式，用这种模式去解决好设备运行维护知识的原始数据资源搜集问题等，对推动此项技术向科学方向发展具有重要作用[1]。数据挖掘和知识发现研究情况表明，对原始信息通过特征提取与有效的特征融合处理，可达到降低数据分类难度、从而提高故障模式分类质量的目的,但这需要对特征属性筛选问题开展深入研究。对于属性筛选，比较肯定的方法包括缠绕法[2]、过滤法[3]等。其中前者特点是筛选出的特征虽然可提高数据分类的准确度，但存在着实现过程复杂、计算量偏大的缺陷；后者借助评价准则对待分析数据及其客观状况进行分析，具有判断各特征属性对分类性能影响的优良作用。其中用到的评价准则包括特征相关性[2]、类间可分性[2]、ReliefF算法[2]、不一致测度[2]、信息增益等指标[2]，以及这些准则间的“串行”与“并行”优化组合[3]等。由于生产实践中旋转机械均是以机组在运行，因此对获得机组运行维护管理知识的数据型知识资源问题，对借助数据驱动去发展关于机组的机器智能技术等，具有非常积极的作用。

基于上述分析，本研究欲以一个双跨转子系统12个通道的测试信息集合为研究对象，对描述转子系统运行状态的敏感特征数据集构造以及解决故障分类问题的方法进行探讨。欲为双跨转子系统运行知识资源的在线积累，提供参考依据。

1 特征选择方法简介

转子系统运行状态描述的敏感特征集构造，涉及到数据挖掘研究中的特征选择问题。该概念意指从原始特征集中，筛选出满足某种评估标准的最优特征子集。这一数据预处理过程是要从一个待分析的数据集中剔除那些影响数据分类质量的不相关和冗余特征，以达到降低数据分类难度为目的。但研究已表明，单一评价准则往往无法准确评价各特征对分类结果的综合影响。为此本研究将针对一个转子系统振动信号集合的一种数据集的有效特征筛选问题，构造出一种串行方式的多准则特征选择方法，即解决故障状态特征空间的维度约简问题。该串行方式涉及的方法包括类间可分性、ReliefF算法等。

1.1 类间可分性判据

为剔除原始数据集中的冗余和不相关特征，本研究欲引用一种基于离差测度的可分离性判据。该判据的出发点是：如果异类样本子集的类间离差越大、类内的离差越小，则类别间的可分性就越好。这一概念的数学定义如下。

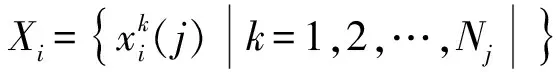
(1)

总的类间离差矩阵：

(2)

其中:Ni为Xi中的样本数；Pi为xi∈Xi的频率；mi(j)为Xi中第j维特征的样本均值；m(j)为整个数据集第j维特征的均值。Sw表征了各类样本子集合围绕其均值的分布状况；Sb则显示出各类间的一种距离测度。将式(1)与式(2)概念集成，一种类间可分性测度可被定义为式(3)形式，即:

(3)

式(3)表明，J值越大的特征,类别可分性越好。故可根据J值的大小，从原始数据集中筛选出敏感特征系列，构成一种敏感特征集合。这种敏感特征集合一般具备能够降低原始数据集分类难度的能力。

1.2 ReliefF算法

原始的Relief算法仅适用于解决二分类问题[4]。目前，一种能够解决多分类问题的改进ReliefF算法已出现。这种改进算法的特点，是它的分类能力更加健全、能够处理不完全和有噪声数据集的多分类问题[5]。该算法的数据处理思想如下。

在总体样本中，xi={xi1，xi2,…，xin}表示第i个样本的n个特征值。对于任意的一个样本xi，首先搜索k个与xi同一类的最近邻的样本实例yj(j=1,2,...,k)，然后在每一个与xi不同类的子集中搜索k个最近邻的样本实例hj(C)(j=1,2,...,k，C≠class(xi))。

设diff_hit表示表示yj和xi在特征上的差异：

(4)

设diff_miss表示hj(C)和xi在特征上的差异：

(5)

特征权重W(xi)的更新依赖于随机选择的样本实例xi、和xi在同类中k个近邻diff_hit，以及和xi不在同一类中的k个近邻diff_miss。权值W(xi)的递推公式如下：

(6)

循环m次ReliefF算法，可得每维特征所对应的W(xi)。该值越大，表明该特征与该类间的相关度越高；越小，表示该特征与该类间的相关度越低。据此可确定出特征属性对分类的影响程度。

2 基于特征选择与特征信息融合的加权KPCA方法

2.1 加权KPCA算法

KPCA方法的主要思想是借助一种非线性映射函数Φ:RN→F，将低维空间的数据集映射至高维空间中，使低维空间中线性不可分的非线性数据集在高维空间中达到线性可分目的。但此法存在着假设所有样本的贡献率相同、不考虑样本权重的影响问题。加权KPCA(WKPCA)方法是对一般KPCA方法的扩展。其基本思想是通过对各个数据特征进行加权，突出不同特征对分类的影响程度作用。

对输入空间的N个样本xi(i=1,2,…,N),xi∈RN,WKPCA分析方法的协方差矩阵如式(7)[6]，即:

(7)

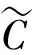
(8)

(9)

2.2 特征选择与多通道特征信息融合的加权KPCA方法设计

单纯依靠特征选择方法无法满足对故障精确分类的要求，因为不同特征对分类的影响程度不同，在分类过程中分类算法可能会被弱相关或不相关的特征所支配，从而影响分类质量。特征加权处理方法，具有强化重要特征、弱化不相关特征的作用，从而对提高分类效果非常有借鉴参考作用。因此，在本研究中提出了一种特征选择与特征信息融合的加权KPCA方法。该方法的数据处理流程如图1所示。其特点是首先采用小节1介绍的特征选择方法剔除不相关与冗余特征，达到数据降维目的；然后采用特征信息融合方法获得多传感器的融合特征向量；最后利用加权KPCA分析方法，提取出融合特征的核主成分。将依据此方法提取出的核主成分解决转子系统故障数据集的准确分类问题。该算法的流程描述如下：

Step1：对每个通道消噪后的故障信号进行时域、频域和时频域的多域特征提取，经归一化处理后构成原始特征集F；

Step2：采用二次特征选择方法对原始特征集进行筛选，选择出利于故障分类的敏感特征集；

Step3: 将从多个通道筛选出敏感特征集进行特征信息融合，并将融合特征分为训练集Ftr和测试集Fte；

上述算法中，为妥善解决好“二次特征选择”问题，构造出一种串行方式的多准则特征选择组合方法，其算法流程见图2。本研究欲借助类间可分性指标和ReliefF算法两者之间的互补性，综合提高筛选特征的分类敏感能力，为一类故障信息的自动获取提供参考。

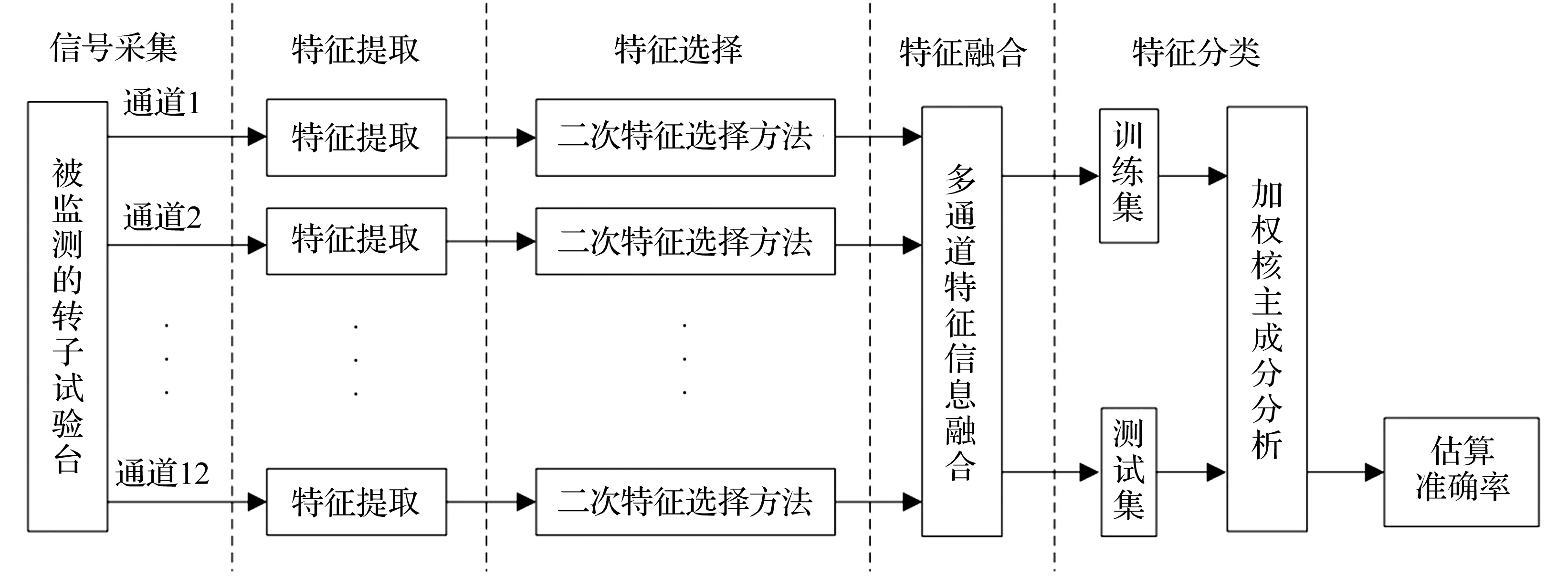
图1 特征选择与特征信息融合的加权KPCA算法流程

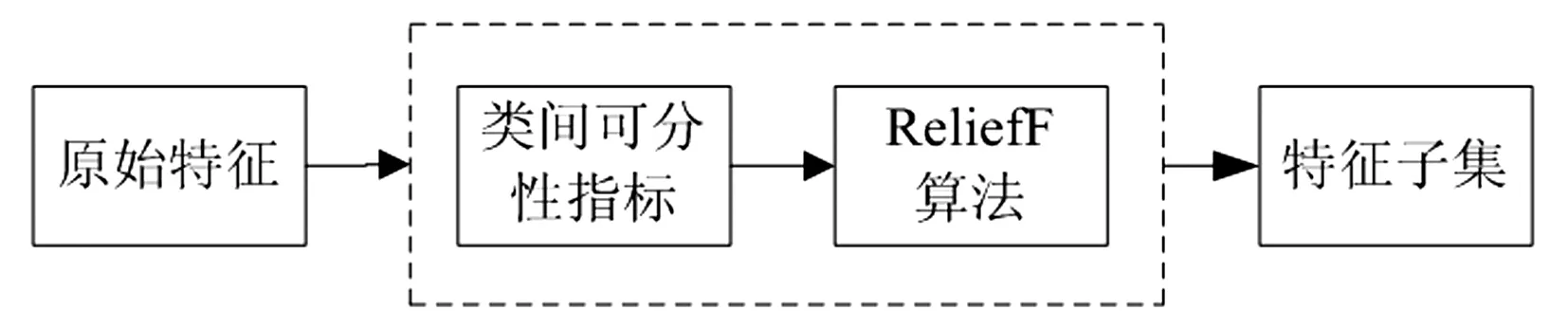
图2 二次特征选择的组合方法

关于“二次特征选择”的数据处理算法如下：

Step1：按照类间可分性判据，分别计算多类情况下样本总的类内离差Sw和类间离差Sb；根据评价准则J值的大小进行一次选择，筛选出敏感特征集D；

Step2：从D中随机选取一个样本xi，在D中找出与xi同类的k个近邻yj(j=1,2,…,k),在其余各类中找出xi的k个近邻hj(C)(j=1,2,...,k，C≠class(xi))，然后按式(6)更新属性的权值，并根据权值大小进行二次特征选择。

3 实验结果与分析

本项研究工作的实验对象见文献[8]图3所示的一套仿真机组结构的双跨度转子系统。在该实验装置上，本研究分别模拟了质量不平衡、转子不对中、碰磨和支座松动四种常见故障类型。采用了在6个关键截面上相互垂直方位上分别布置的共12个涡流传感器方式，拾取转子系统的振动信号，并进行消噪处理。按照2.2节所述的算法流程对故障信号进行原始数据集构造及算法应用，应用结果情况分别如下。

3.1 初始特征提取情况

为能够全面客观地反映出文献[8]图3转子系统的运行状况，研究中采用了将时域、频域、时频域特征集成在一起构造出单个通道信号的原始特征子集合方法。出于对双跨度转子系统振动状态的尽可能全面描述之目的，设计出的单一通道信号的特征集合如表1。它由共29个特征作为单个通道信号的初始特征集。按照通道编号将其拓展至12个通道，据此规则构造出了一种多域特征集合的双跨转子系统原始特征集合，作为具体的研究对象。

表1 特征参数

3.2 特征选择与特征信息融合的分析应用

以ch2单通道信号为例，按照图2流程进行特征选择，一次选择结果如图3所示。图中，每条线的高低代表着可分性指标J值的大小，线顶圈起来的特征表示选择出的敏感特征。从图3中可知，按照可分性指标大于0.6的原则从29个原始特征中选择出6个特征作为敏感特征，他们分别是P6、P11、P12、P13、P25、P28标号对应的特征。

图3 单一通道信号的原始特征集构造

采用ReliefF算法对敏感特征集进行二次特征选择，并计算特征权值。其中,循环次数m=30，计算得到加权矩阵W=[0.773 8，1.724 4，4.136 9，3.315 5，2.500 6，0.303 9]。权值矩阵中的第三个特征的贡献程度最大，第六个特征的贡献程度最小，基本符合一次特征选择结果中特征指标大小的分布情况。然后剔除权值小于1的特征。经二次选择得到P11、P12、P13、P25标号对应的特征，以及归一化后的加权矩阵w=[0.147 7，0.354 4，0.283 7,0.214 2]。

按照上述方法，分别对12个通道原始特征集进行选择并融合，处理结果如表2。表2中分别列举了不平衡、不对中、碰磨和松动四类常见故障各80组样本，各通道的29种特征经过二次特征选择后得到4种敏感特征，对上述敏感特征进行融合，得到故障特征数据表可作为WKPCA方法的依据。

3.3 WKPCA的分析应用情况分析

将从多通道数据集选出的融合特征向量引入核函数空间，采用高斯径向基核函数，对于核函数参数的选取问题，采用夹角余弦测度构造适应度函数[7]，运用粒子群优化算法对核函数参数寻优。其中设置进化代数N=100，种群规模大小pop=30，通过计算得出加权特征的核参数σ结果见表3。

为了使实验更有说服力，实验中分别选用一般KPCA方法、特征选择后的KPCA方法和特征选择融合后的加权KPCA方法提取核主元特征，提取的结果如表3所示。其中，分别提取了故障样本的前4个主元特征，并计算其贡献率和累计贡献率。可以看出特征选择KPCA方法的累积贡献率要小于一般KPCA方法，表明前一方法的提取结果所包含的故障信息有所减弱，这是因为采用特征选择方法直接去除部分特征信息，但是去除的特征对于提取结果的影响并不大。而特征选择融合的WKPCA方法较于二者，其所包含的故障信息有所提高。

然后给出四种类别故障情况下的核主元特征点在前两组特征向量下的二维分布情况见图4。其中,“o”、“+”、“*”、“Δ”分别表示不平衡、不对中、碰磨和松动四种故障的核主元特征。图(a)中采用一般KPCA方法提取的结果分布较散，并且类别2与类别3的样本点混叠情况严重。图(b)采用特征选择KPCA方法的效果有所改善，但是样本点沿着某一方向的分布集中，而沿着其他方向的分布较散，并且故障类别2的样本点过于分散。图(c)中采用特征选择融合的WKPCA方法使得各故障样本点的分布更加集中，类别间距明显，识别效果好。

表2 多传感器融合的故障特征数据表

表3 三种特征提取方法的主元贡献率

为进一步验证本研究的有效性，采用SVM分类器对原始故障数据特征及采用了三类KPCA特征提取方法的结果进行分类，结果见表4。其中，分别计算每一故障类别对比其余故障类别的分类准确率[8]。可以看出，由于原始特征中存在诸多的冗余特征与不相关特征，分类结果受到极大的影响，分类准确率低；第一种方法对各类别的分类辨识度都不高，第二种方法的辨识效果有所改善，第三种方法的识别效果最优，其每一种故障类别的分类准确率均可达到100%。

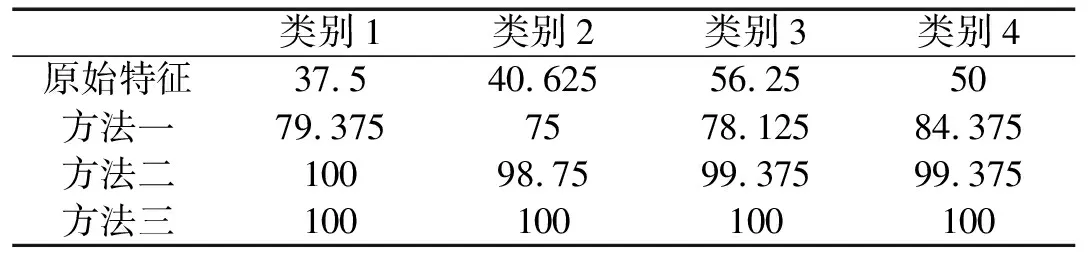
表4 SVM分类辨识方法的准确率(%)

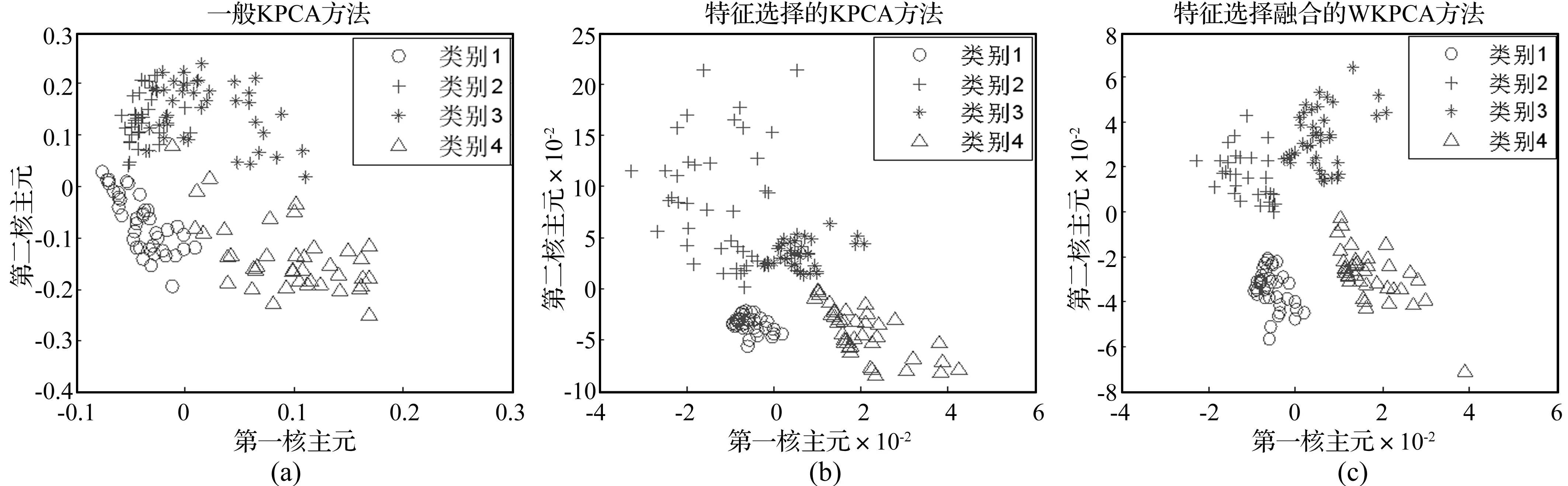
图4 测试样本的分离效果

4 结 论

为解决旋转机械动力机组故障数据集的分类问题，提出了一种特征选择与特征信息融合的加权KPCA方法。该方法采用二次特征选择的组合设计，这种设计不仅能去除冗余特征的缺陷，并且具有强化重要特征、弱化不相关特征的作用；采用特征信息融合方法提高了分类精度；运用WKPCA分析方法，具有对非线性数据较好的处理能力。双跨转子系统典型故障数据集的应用情况表明，将该方法用于典型故障信号的量化特征提取中，可有效地显现出不同故障类别间的较显著差异，为解决好故障数据集的类别划分问题，提供了一种新途径。

[1]胡金海,谢寿生,侯胜利,等.核函数主元分析及其在故障特征提取中的应用[J].振动、测试与诊断，2007，27(1):48-52.

HU Jin-hai，XIE Shou-sheng，HOU Sheng-li，et al.Kernel principal component analysis and its application to fault feature extraction[J].Journal of Vibration，Meaturement & Diagnosis，2007，27(1):48-52.

[2]杨艺,韩德强,韩崇昭.基于排序融合的特征选择[J].控制与决策，2011，26(3):397-401.

YANG Yi，HAN De-qiang，HAN Chong-zhao.Study on feature selection based on rank-level fusion[J].Control and Decision，2011，26(3):397-401.

[3]李勇明,张素娟,曾孝平,等.轮询式多准则特征选择算法的研究[J].系统仿真学报，2009，21(6):2010-2013.

LI Yong-ming，ZHANG Su-juan，ZENG Xiao-ping，et al.Research of poll mode and multi-criteria feature selection algorithm based on chain-like agent genetic algorithm[J].J of System Simulation，2009，21(6):2010-2013.

[4]Kira K，Rendell L A.The feature selection problem: Traditional methods and a new algorithm [C].Proceedings of the 9th National Conference on Artificial Intelligence.[S.l.]: AAAI Press，1992:129-134.

[5]Kononenko I.Estimation attributes: Analysis and extensions of RELIEF[C]//Proceedings of the 1994 European Conference on Machine Learning.[S.l.]: ACM Press，1997:273-324.

[6]Wang F，Wang J D，Zhang C S，et al.Face recognition using spectral features[J].Pattern Recognition，40(10):2786-2797(2007).

[7]李晓宇,张新峰,沈兰荪.一种确定径向基核函数参数的方法[J].电子学报，2005，33(12):2459-2463.

LI Xiao-yu，ZHANG Xin-feng，SHEN Lan-sun.A selection means on the parameter of radius basis function[J].Acta Electronica Sinica，2005，33(12):2459-2463.

[8]霍天龙,赵荣珍,胡宝权.基于熵带法与PSO优化的SVM转子故障诊断[J].振动、测试与诊断，2011，31(3):279 -284.

HUO Tian-long，ZHAO Rong-zhen，HU Bao-quan.Fault diagnosis for rotor systems based on entropy band method and support vector machine optimized by PSO [J].Journal of Vibration，Measurement & Diagnosis，2011，31(3):279-284.