V型折叠式夹层板横向压皱吸能特性研究

张延昌， 俞鞠梅， 张世联， 周 红， 王自力

(1．江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003; 2．上海交通大学 船舶海洋与建筑工程学院，上海 200030)

随着粘结及激光焊接技术的发展，夹层板结构的各种优越性能逐渐得到体现与证实，并受到各工程领域的青睐。夹层板结构作为轻型结构在航空、航天、飞机、汽车等领域得到广泛地应用。考虑到舰船、船舶恶劣的工作环境、舰船结构及设计载荷的复杂性、结构设计要求较高等因素，夹层板在船舶结构中的应用起步较晚。近些年各国海军、船级社、科研院所等陆续开展了夹层板制造、性能、设计等方面的研究工作[1-6]，目的在于设计出性能优良、成本低廉、更安全可靠的船舶结构。

金属夹层板按其夹芯类型可分为蜂窝式、折叠式、桁架式、混凝土夹层板等，折叠式夹芯层结构是连接上下面板的中间结构，对夹层板力学性能的发挥尤其是吸能特性起关键作用，折叠式金属夹芯层结构的吸能效率是夹层板结构防护性能的决定因素[1]。Xue等[7-8]采用简化理论分别对四边形蜂窝、折叠式、桁架式夹芯层结构的动态压溃响应进行了分析。Tilbrook等[9]对折叠式、Y型夹芯层结构动态压溃响应进行了试验研究，并与数值仿真分析进行对比分析。Aktay等[10]提出几种数值仿真分析技术，并用于Nomex蜂窝夹芯结构动态压溃行为分析，同时还对其进行准静态压缩试验研究。Coté等[11]通过数值仿真及试验研究分析了金属蜂窝夹芯层横向压溃性能，基于夹芯层单元弹性及塑性屈曲提出简化理论分析模型，并与试验结果进行对比，结果吻合较好。张延昌等[12-13]曾对U型夹芯层的横向准静态压皱性能进行了试验及数值仿真研究，研究夹芯层结构在准静态下的压皱力学行为及吸能特性，为夹层板防护结构设计提供了指导。本文以V型夹芯层结构为研究对象，通过准静态试验分析夹芯层在横向压皱载荷下的力学行为，分析夹芯层结构的吸能特性，研究变形模式对吸能特性的影响；并与数值仿真分析结果进行对比分析，验证有限元分析技术。

1 试验研究

1.1 试件设计及加工

试件夹芯层结构由V型折叠式单元在侧向方向上拓扑而成，夹芯层与上下面板之间通过焊接连接，如图1(a)所示。理论上说夹芯层结构在侧向单元个数越多，单元边界的影响越小，考虑到工程实际、试验装置、试验条件等限制，试件侧向取4个单元长度；纵向结构尺寸并不会对夹芯层结构的压皱性能产生明显影响，试件纵向长度取100 mm。

试件材料为船用低碳钢Q235，采用传统电弧焊接工艺加工制造而成。焊接过程若采用合理的焊接工艺可减小焊接变形，V型夹芯层结构制造工艺流程图如图1(b)所示。夹芯层壁板及上下面板的厚度均为3.5 mm，夹芯层与面板之间的角焊缝的焊址高度为3～4 mm。

图1 V型夹层板结构及装配图

图2 试件塑性变形施加示意图

1.2 准静态压皱试验方案

本试验测量夹芯层结构在横向载荷下的压皱行为，夹芯层壁板在压皱载荷下发生屈曲、塑性铰及塑性铰滑移等，应用防护结构设计达到吸收能量的效果。试验研究的关键在于试验装置设计及变形模式控制。实际夹层板结构在横向载荷下，上下面板受到约束作用不会产生侧向位移，为了限制上下面板的侧向移位，试验设计了试件支架装置来限制了上下面板之间的侧线位移。试验开始前将试件与加载板、支架结构通过压板条由螺栓连接在一起，当试件夹芯层发生压皱屈曲后(压皱位移接近1/4夹芯层高度)，卸去螺栓及压板条，使得夹芯层被压实。为了控制试件的变形模式，对试件3-2在每片夹芯层纵向两端壁板高度中间区域局部施加塑性变形作为初始缺陷，局部塑性变形量大小约为3～4 mm，示意图如图2所示。

试件与支架之间通过压板条螺栓连接在一起，试件放置于试验机工作平台上，通过支架两端的角钢卡在工作平台两侧以限制支架的位移；试验机作动器载荷通过厚度为50 mm的加载板施加于试件，以保证均匀加载。试验装置示意图如图3所示。在试验前预压10 kN的压力，消除安装间隙及试件的不平整。试验时通过位移加载，加载速率为5 mm/min，载荷位移数据由计算机自动记录，采样频率为10 Hz，压皱损伤变形图由数码相机拍摄。

图3 压皱试验装置示意图

1.3 试验结果分析

试验得到载荷位移曲线、结构的变形图，结果分析主要根据载荷位移曲线分析结构的压皱载荷、结构的吸能，并结合损伤变形图分析夹芯层结构的变形模式及压皱渐进屈曲过程。

夹芯层结构单元在横向压力作用时将发生失稳屈曲，每个夹芯薄板均有两个屈曲方向：向上,向下。相邻两片夹芯薄板的变形模式称为单元变形模式，根据两片夹芯板屈曲变形的方向，可分为单元变形模式I和单元变形模式Ⅱ两类，如图4所示，压皱过程中关键位置的变形图如图5所示。单元变形模式Ⅰ——相邻的两片夹芯板同时发生向上或向下的屈曲变形，该变形模式所对用的相邻夹芯板的变形方向有两种组合。单元变形模式Ⅱ——相邻的夹芯板分别发生向上、向下的屈曲变形，该变形模式所对应的相邻夹芯板的变形方向有四种组合。

图4 V型夹层板单元变形模式

图5 单元变形模式Ⅰ和Ⅱ的变形过程图

试验得到的V型夹层板的变形模式均为这两种单元变形模式的组合，试件V3-2由4个单元变形模式Ⅰ组成，称之为变形模式A；试件V2-1、V2-2由2个单元变形模型式Ⅰ和2个单元变形模式Ⅱ组成，称之为变形模式B。

(1)压皱力

试验得到3个V型夹芯层试件的压皱力-位移曲线如图6所示。压皱曲线相似，可分为首次峰值段、二次峰值段、压实段三阶段；首次峰值段即为阶段Ⅰ，夹芯层薄板受压载荷迅速上升，夹芯层发生屈曲失稳，载荷达到第一峰值载荷。在高度中间形成塑性铰线，载荷下降后趋于稳定。若相邻的两片夹芯结构同时发生向上或向下的屈曲变形，则两片夹芯层板将形成“漏斗”型的变形模式，如图4(a)所示；随着压皱位移的增加，在夹芯层与上下面板相连接区域形成塑性铰线，两片夹芯层板中间塑性铰线附近相互接触，变形进入阶段II；若相邻的两片夹芯结构分别发生向上、向下的屈曲变形，随着压皱位移的增加，相邻夹芯层板不会相互接触，夹芯板折叠后与面板接触进入阶段II，如图4(b)所示。在这一阶段两不同屈曲方向引起的3种变形模式所对应的载荷、变形模式、压皱行程等力学特性基本相同。

二次峰值阶段(阶段Ⅱ)：随着压皱位移的增加产生“漏斗”型变形模式的相邻两片夹芯层及夹芯层与面板开始相接触，结构压皱力再次上升，并出现第二个峰值；随后发生接触的夹芯层壁板再次发生屈曲并形成塑性铰线，形成“菱形”的变形屈曲模式。两不同屈曲方向所对应的载荷及变形存在较大的差异性，单元变形模式Ⅰ的个数越多第二峰值载荷及平均压皱载荷越大。试件V3-2的变形模式为模式A(由4个单元变形模式Ⅰ组成)，其第一峰值载荷为：331.0 kN，第二峰值载荷为：636.1 kN；试件V2-1、V2-2的变形模式为模式B(由2个单元变形模式Ⅰ和2个单元变形模式Ⅱ组成)，对应的峰值载荷分别为：420.5 kN～444.5 kN、440 kN 。

图6 试件压皱力-位移曲线

图7 V型夹层板压皱变形图

随着压皱行程的增加，当压皱位移达到100 mm左右夹芯层结构被压实，压皱力迅速增加，变形进入第三阶段压实阶段。不同变形模式的最大压皱行程基本相同。

(2)损伤变形

试验得到V型夹层板损伤变形图如图7所示，反映了夹芯层压皱渐进屈曲过程，可见两种单元变形模式的显著区别在于两片相邻夹芯板是否接触。结合图6可知，在相邻夹芯板接触前两种单元变形模式所对应的峰值载荷、压皱力-位移曲线基本相同；在变形模式Ⅰ中，由于相邻夹芯板的接触约束使得压皱力再次上升，呈现第二个峰值，这也影响夹层板压皱性能的关键因素。

(3)吸能效率

评估吸能结构的吸能效率的主要性能参数有：比吸能Se、平均压皱强度σm、压皱行程δ等[13]。试验测得压皱力学性能参数如表1所示，变形模式B所对应2个试件的力学性能参数基本相同，与变形模式A所对应的试件V3-2相比，比吸能、平均压皱强度低10 %左右。

表1 V型夹层板压皱性能参数

试件的变形模式是由单元变形模式组成，夹芯层结构压皱后产生的变形模式中单元变形模式Ⅰ、Ⅱ的个数决定了其压皱力学性能。变形模式不同的结构，其压皱性能相差较大，而变形模式相同的结构压皱性能基本相同，变形模式对夹芯层的压皱力学行为影响较大。单元变形模式Ⅰ的吸能效率(比吸能、平均压皱强度)要高于单元变形模式Ⅱ，变形模式A所对应的压皱性能优于变形模式B的压皱性能。同时试件V3-2所施加的塑性变形对结构的第一峰值载荷有较大的影响，第二峰值载荷由变形模式控制，受初始塑性变形影响较小。

2 数值仿真分析

2.1 仿真分析计算方案

本文作者曾[14]对夹层板横向压皱数值仿真分析技术进行了研究整理，本文对数值仿真分析方案进行简要叙述。采用非线性有限元软件Abaqus数值仿真分析夹芯层压皱力学行为，以重锤低速撞击夹层板模拟准静态压皱载荷，其中重锤重量为10 000 kg，撞击速度为1 m/s；上面板仅放松横向线位移(Z向)，下面板采用刚性约束。

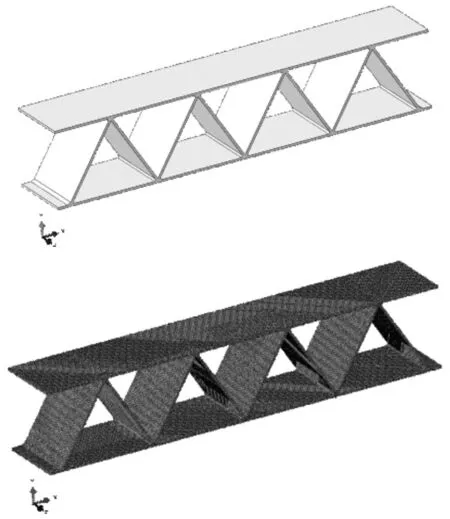
图8 夹层板有限元模型

结构有限元模型如图8所示，夹芯层、面板、焊缝等均采用Hex体单元建模，单元边长尺寸为夹芯层板厚的一半，网格大小约为2 mm。焊缝材料与夹芯层、面板相同均为船用低碳钢，采用Cowper-Symonds弹塑性材料模型，考虑应变率敏感影响，其中D=40，P=5。夹芯层、面板之间定义接触，其中接触摩擦系数为0.3。

在有限元结构模型中，为了得到与试件相同的变形模式，在每片夹芯层壁板高度中间所有节点施加相同的塑性变形作为初始缺陷(如PD0.1表示初始塑性变形为0.1 mm)，初始塑性变形沿纵向均匀施加，对于变形模式A分析了不同初始缺陷值对计算结果的影响。

2.2 仿真结果分析

(1)压皱力-位移曲线

有限元数值仿真分析得到的载荷位移曲线如图9所示。与试验结果对比，数值仿真与试验方法分析得到的结果基本吻合，说明本文采用的有限元模型技术可以准确地分析夹芯层的压皱性能。

有限元数值仿真分析得到的第一峰值载荷比试验值要高，第二是峰值载荷基本相当，但第二峰值位置所对应的压皱行程稍大，即第二峰值出现的相对较晚。有限元模型中不同初始缺陷对载荷位移曲线的第一阶段产生一定影响，初始变形越大所对应的峰值压皱载荷越小，但初始缺陷对曲线第二阶段的影响较小。

图9 试验与数值仿真载荷位移曲线

(2)损伤变形

有限元分析得到典型压皱位置所对应的损伤变形图如图10所示，可以清楚地反映各位置处的损伤变形模式及夹芯层压皱渐进屈曲过程，变形模式与试验结果一致。不同初始塑性变形量对应的压皱变形模式基本一致，图9给出了塑性变形量为0.1 mm的变形图。

图10 V型夹层板损伤变形图(有限元)

(3)吸能效率

夹芯层结构吸能性能参数如表1所示。有限元模型为理想化结构模型，仅考虑了塑性变形初始缺陷，没有考虑试件其它方面如几何缺陷、焊接残余应力、焊接变形等等对压皱性能的影响，比试验结果测得的平均压皱力、比吸能、峰值载荷等性能参数均偏高。初始塑性变形初始缺陷越大结构吸能效率越低，但其相对误差在10 %左右，初始塑性变形主要影响第一峰值载荷，数值仿真采用施加初始塑性变形以得到特定变形模式的处理方式是合理的。

3 结 论

通过试验、数值仿真分析了V型夹芯层结构在横向压皱载荷下的准静态行为及其压皱性能，得到了夹芯层结构压皱吸能机制及其吸能特性，主要研究结论如下：

(1)试验、数值仿真分析表明，V型夹芯层结构在横向压皱载荷的发生屈曲、褶皱变形模式，产生塑性铰及塑性铰滑移等吸收了大部分能量，得到了V型夹层板在横向压皱载荷下的变形模式、压皱力，分析结果吻合较好，验证了数值仿真分析具有可靠的计算精度。在开展新式结构设计、结构防护性能等研究等方面，采用合理的有限元模型化技术的数值分析方法比试验方法具有更可行、高效。

(2)提出了两种单元变形模式，夹芯层的变形模式由单元变形模式组合而成，单元变形模式的个数决定了结构的压皱性能，夹芯层可设计成特定形状以控制夹芯层结构变形模式，提高结构的吸能效率；随着初始缺陷塑性变形量的增加，夹芯层的第一峰值载荷、平均压皱力、比吸能等性能参数降低，对第二峰值载荷及压皱行程基本没有影响。单元变形模式I的吸能效率较高，控制夹芯层结构压皱变形模式可以充分发挥夹芯层吸能特性。

(3)夹芯层结构在横向载荷作用下，具有较高的第一峰值载荷、较长的有效压皱行程、平稳的压皱载荷，表现出良好的吸能特性，V型夹层板可用作防护结构设计。

(4)试验过程中施加塑性变形来控制夹芯层的变形模式，有待于进一步开展针对于该缺陷对数值仿真分析结果的影响。

致谢

感谢江苏科技大学工程力学实验室沈超明老师在试验过程中给予的帮助与指导。

参 考 文 献

[1]张延昌. 水下爆炸冲击载荷下折叠式夹层板防护性能研究[D].上海：上海交通大学,2012.8.

[2]岳灿甫, 吴始栋. 国外船用激光焊接波纹夹芯板的开发与应用[J]. 鱼雷技术, 2008, 15(4):1-5.

YUE Can-fu, WU Shi-dong. Introduction to development and applications of marine laserwelded lightweight sandwich panel in the us navy and european countries[J].Torpedo Technology, 2008, 15(4):1-5.

[3]Kujala P, Klanac A. Steel sandwich panels in marine applications [J]. Brodogradnja, 2005, 56(4)：305-314.

[4]Kumar P， Dharmasena, Haydn N G， et al. Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading[J]. International Journal of Impact Engineering, 2008, 35:1063-1074.

[5]王盛春，邓兆祥，王 攀，等. 四边简支条件下正交各向异性蜂窝夹层板的固有特性分析[J]. 振动与冲击,2012, 31(9)：73-77,89.

WANG Sheng-chun，DENG Zhao-xiang,WANG Pan，et al. Connatural characteristics analysis of rectangular orthotropic honeycomb sandwich panels with all edges simply supported[J]. Journal of Vibration and Shock，2012, 31(9)：73-77,89.

[6]黄 超，姚雄亮，张阿漫. 钢夹层板近场水下爆炸抗爆分析及其在舰船抗爆防护中的应用[J]. 振动与冲击,2010, 29(9)：73-76.

HUANG Chao，YAO Xiong-liang，ZHANG A-man. Analysis on blast-resistance of steel sandwish plate under proximity underwater explosion loading and its application inship protection[J]. Journal of Vibration and Shock,2010, 29(9)：73-76.

[7]Xue Z Y， Hutchinson J W. Crush dynamics of square honeycomb sandwich cores[J]. International Journal for Numerical Methods in Engineering, 2005,65：2221-2245.

[8]Vaziri A， Hutchinson J W. Metal sandwich plates subject to intense air shocks[J]. International Journal of Solids and Structures, 2007,44:2021-2035.

[9]Tilbrook M T， Radford D D， Deshpande V S，et al. Dynamic crushing of sandwich panels with prismatic lattice cores[J]. International Journal of Solids and Structures, 2007, 44:6101-6123.

[10]Aktay L，Johnson A F， Kroplin B H. Numerical modelling of honeycomb core crush behaviour[J]. Engineering Fracture Mechanics, 2008,75(9):2616-2630.

[11]Coté E， Deshpande V S， Fleck N A， et al.The out-of-plane compressive behavior of metallic honeycombs[J]. Materials Science and Engineering A, 2004,380:272-280.

[12]张延昌，王自力，张世联. 折叠式夹芯层结构耐撞性能研究[J]. 船舶力学，2010，14(1-2)：114-120.

ZHANG Yan-chang, WANG Zi-li, ZHANG Shi-lian. Simulation analysis of folded core structure under dynamic load[J]. Journal of Ship Mechanics, 2010,14(1-2):114-120.

[13]Zhang Y C， Zhang S L， Wang Z L，et al. Quasi-static compressive behavior of U-type corrugated cores sandwich panels[J]. Journal of Ship Mechanics,2012,16(12)：1417-1426.

[14]俞鞠梅, 周 红, 张延昌.折叠式夹层结构压皱性能数值仿真 [J]. 计算机辅助工程，2013,22(3)：63-70.

YU Ju-mei, ZHOU Hong, ZHANG Yan-chang. Numerical simulation analysis of compressive behavior of folding core structure[J]. Computer Aided Engineering，2013,22(3)：63-70.