基于声-超声技术的木材弹性模量测定方法研究

徐 锋， 刘云飞， 潘惠新

(1.南京林业大学 信息科学技术学院，南京 210037；2.南京林业大学 森林资源与环境学院，南京 210037)

木材的弹性模量是表征木材弹性力学性能最基本也是最重要的指标之一，代表了木材力学性能的综合情况，是实现木材力学性能无损检测及强度在线自动分级的重要参数和依据[1]。目前公认检测木材弹性模量的标准方法为静态弯曲法，但该方法测量过程繁琐，测量时间相对较长，同时对木材具有破坏性，其已不能满足连续化生产的需要。

无损检测因具有不破坏材料的原有特性、能在短时间内获得期望的结果、操作速度快、有利于连续生产和提高生产效率等优点，在木材工业中得到了广泛的应用。超声波检测是木材无损检测技术中应用最广泛的方法之一，国内外有众多的专家学者在这方面做了大量研究，并取得了一定成果。文献[2-6]分别利用超声波纵波传播法和纵波共振法对板材动态抗弯弹性模量进行了检测，并将结果与静曲弹性模量进行对比，得出两者之间呈线性相关；文献[5-6]还指出通过快速傅里叶变换(Fast Fourier Transform ,FFT)测共振频率计算弹性模量比声速法计算弹性模量准确性更高。

虽然直接FFT方法得到的动态弹性模量与静曲抗弯模量在数值大小以及相关性方面比声速方法更准确，但仍然与静曲抗弯模量有20%左右的偏差[7-10]。研究发现，此偏差主要归因于噪声和传感器谐振频率对准确提取信号基频影响所致。因此，本文提出改进的声信号基频(共振频率)提取算法——最大公约数算法，提取信号基频并依此计算木材的弹性模量，最后作线性回归分析，并与FFT方法作出比较。

1 声-超声动态弹性模量测试原理

声-超声测试原理如图1所示。在试件的一端由发射换能器激发一超声脉冲信号，使之沿测试试件长度方向传播，穿透信号由试件末端的接收换能器接收。分析可知，超声脉冲信号频域内可以等效成一含多频率分量的激振，只要脉宽合适，激振信号中一定包含等于或接近试件固有频率的信号，即接收信号中一定出现谐振响应现象，由此得到谐振频率。根据两端自由棒振动理论公式[11]：

(1)

由测定的共振频率、试件密度及试件长度即可得出被测试件的动态弹性模量。式中，E为动态弹性模量，ρ、l分别为试件密度和有效长度，fn为第n次谐振频率，n为谐振次数。

图1 声-超声测试原理图

2 噪声及传感器谐振频率对共振频率的影响

木材纵向振动属于连续弹性体振动，具有无限多自由度及其相应的固有频率和主振型，其振动可表示为无穷多个主振型的叠加。当受到一含多频率分量的脉冲激振时，接收传感器拾取的信号频谱中应包含非常明显的谐振频率带。然而由于木材的固有频率较低，受接收传感器谐振频率影响，往往低频段的谐振频谱会被淹没，尤其在有脉冲干扰和随机噪声下，情况更为严重。这时如把较高次谐振频率混淆作为基本谐振频率而代入公式计算弹性模量，其值通常会比标准力学方法得到的值大很多(虽然两者相关性较好)。因此，从接收信号中提取振动信号基频或确定较高次谐振频率的阶次是解决这一差值的关键。

3 基于最大公约数算法的谐振频率提取

3.1 基频估计预处理

对采集信号进行傅里叶变换得到信号频谱，由于噪声干扰以及接收传感器谐振频率的影响，频谱中会出现除共振基频和谐频以外的干扰峰，这些干扰峰可能会淹没低频段的谐波峰，也可能因其峰值较大而被误认为是木材的共振基频或倍频，导致对共振基频的误判，从而使计算的弹性模量值欠佳。分析可知，木材共振频率及其倍频处谱峰最显著的特点是比邻域谱峰峰值更大(不是整个频段)，因此，根据此特点可将谱峰识别作如下预处理：

(1)假设信号频谱序列的幅值为A(n)，n=1,2,…,N,N为频谱序列长度，令第i(1≤i≤N)点对应的谱幅为A(i)，按式(2)求谱幅的一阶差分序列ΔA(i)。

ΔA(i)=A(i+1)-A(i)

i=1,2,…,N-1

(2)

(2)局部最大峰值点判断：若ΔA(i)>0且A(i+1)<0，则A(n)为局部极大峰值点，反之，则为中间点，舍去。

(3)根据木材共振基频的可能取值范围，设置最大值点判别区间，即在每一个极值点对应的频率区间搜寻最大值点，不是最大值的全部舍去。

(4)以剩余谱线的幅度均值为阈值进行门限设置，幅值大于阈值的，认为是可能的谐振频率点而保留，反之，则认为是噪声干扰谱线予以去除。

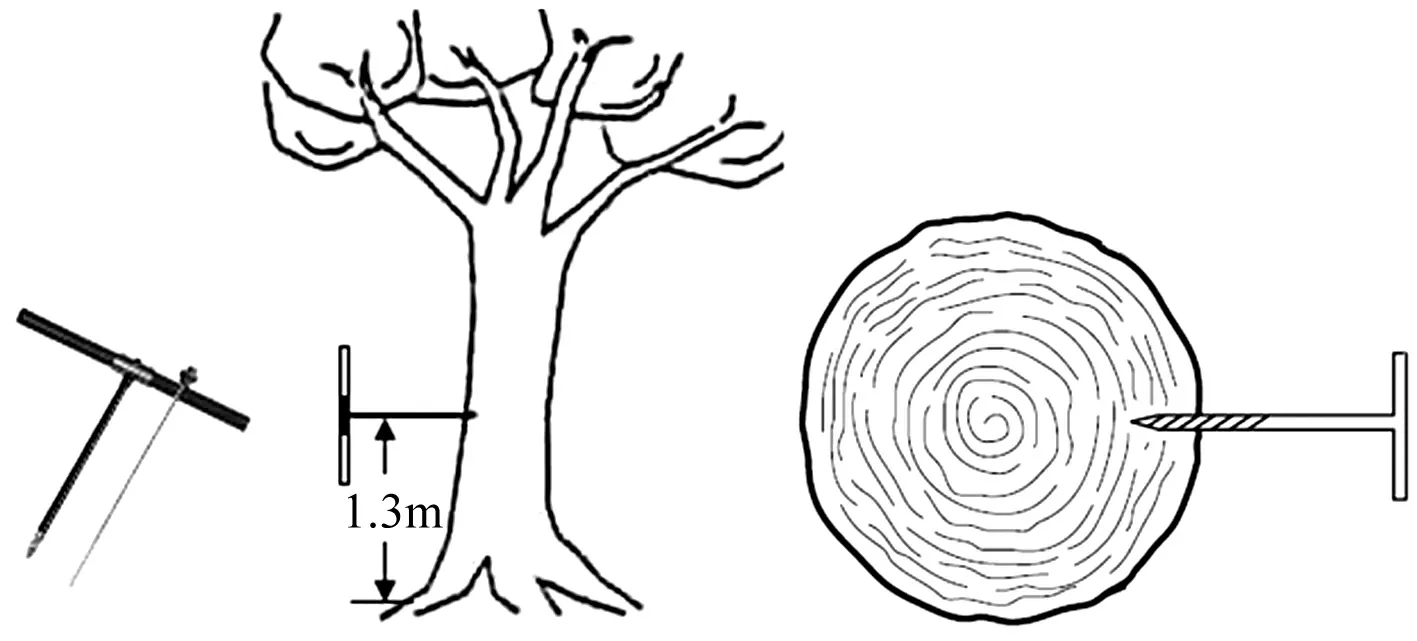
经过以上预处理后，保留的i(2≤i

3.2 最大公约数算法及谐振频率提取

经过预处理后的i根谱线fm(m=1,2,…,i)虽然较为纯净，但由于传感器谐振频率的影响，可能已使部分低频共振频率丢失，或者可能由于噪声干扰，产生了若干虚假谱线，因此，对预处理后的谱线仍需进一步来确定信号的谐振频率。理想上，振动信号的谐波族中相邻谱线间的间隔是相等的，而虚假谱线不具有此特性，因此可用最大公约数算法进行提取。

(1)求取差频：设经预处理后的频谱有i根有序谱线fm(m=1,2,…,i)，分别求取两两之差：

Δfjk=fj-fk,j,k=1,2,…,i;j>k

(3)

设置差频取值范围(跟木材共振基频相关)，将落在区间外的差频值舍去，并将保留的差频序列从小到大排序，得到差频数组{Δfjk}。

(2)定义品质因数an：差频数组{Δfjk}中可能含有相等或近似相等的元素，统计在容限范围内相同差频的个数，定义为品质因数an，an即为每个相同差频的个数。相同差频只保留一次，记为Δfr。设新得到的差频有M个，记为数组{Δfr},r=1,2,…,M。

(3)定义品质因数bn：用每一根线谱fm(m=1,2,…,i)去除以差频数组{Δfr}中的每一个差频，每一个差频Δfr对应一品质因数，其定义为bn。若

|fm/Δfr|-[fm/Δfr]|<Δ

m=1,2,…,i;r=1,2,…,M;fm≥Δfr

(4)

成立，则Δfr所对应的品质因数bn加1。bn值代表谱线序列fm(m=1,2,…,i)中有bn根线谱是差频Δfr的倍数。式中， [ ]表示取整， Δ为误差控制量，其值与差频Δfr的大小有关。

(4)定义品质因数cn：cn=an×bn。

(5)共振频率的确定：品质因数cn的最大值对应的差频即为木材的共振频率。当不同差频所对应的品质因数cn相同时，取对应品质因数bn最大的；当品质因数bn也相等时，就要先分析这两个线谱频率是否成谐波倍数关系，满足则取小的那个频率，不满足则选取差频大的那个频率，因为在相同的条件下数越大越不容易被整除。

4 实验与分析

4.1 材料与方法

试材为江苏省徐州市铜山区张集林场的速生杨木(NL-6583)，16年生。随机选取30株，在胸高1.3 m处沿同样的半径方向从活树上用生长锥钻取木芯，钻取示意图如图2所示。从每根木芯上截取一段作试样，紧靠树皮方向，共计30段。试样长度为100 mm，直径为5 mm。同时在钻取木芯的附近位置切取方木，制作标准试件(20 mm×20 mm×300 mm)，以供标准力学方法作比较测试，试样如图3所示。

样品放置于温湿度相对稳定的实验室气干，气干后置于调温调湿箱(20℃，65%RH)中平衡处理，一周后取出。样品气干密度为379～456 kg/m3，含水率为10%±1%。试验测试温度为25℃，测试原理如图1所示。超声波脉冲由美国PAC公司的任意波形发生器ARB-1410激发，脉宽为1.25 μs。采集系统为配套的PCI-2声发射采集系统，采样频率为1 MHz。

试验中为保证传感器与试材截面良好耦合，制作了楔形波导，并用真空润滑脂作为耦合剂耦合。

图2 树木生长锥取样示意图

图3 杨木测试试样图

4.2 结果与分析

图4是杨木木芯实测信号(已按文献[12]降噪)的频谱图。从频谱图中可以看出由于噪声和传感器谐振频率的影响，信号的低频部分很模糊，幅值很小。直接FFT提取的基频通常认为是幅值最大点所对应的频率值，本图中即取58.47 kHz，代入公式(1)，计算可得杨木的动态弹性模量约为38.69 GPa。图5是经3.1节第1、2步预处理后的频谱图，图中一些中间点和干扰峰已被去除，部分谐振频率已基本显现出来了，但确定基频较难。图6是3.1节第3、4步进一步处理后的频谱图，图中剩余线谱中部分频率明显成谐波倍数关系，但少数干扰峰依然存在，需进一步利用最大公约数算法来精确提取信号基频。

从最大公约数算法处理完的实验结果中挑选典型的差频，将其对应的三个品质因数列于表1中。依据3.2节共振频率确定原则，信号的基频落在28～30 kHz之间。另外，从表中可得57～59 kHz之间的差频对应的品质因数也较大，此正符合振动系统无穷多个主振型的叠加特性，说明此差频定为振动信号高次谐波频率。参考图6，确定基本共振频率值为29.17 kHz，代入公式得到动态弹性模量为16.63 GPa。用标准力学方法测试标准试样[13]，得到静曲弹性模量值为15.93 GPa。实验结果和力学方法值非常相近，比直接FFT数值更加准确。对30组样本进行相同测试，试验结果列于表2(本文方法获得的动态模量记为Eu，FFT所得动态弹性模量记为Ef，力学方法获得的静曲弹性模量记为Es)。

试验结果表明，两种无损检测方法所测得的动态弹性模量值均高于静曲抗弯弹性模量(原因为超声方法所用的脉冲很短，声波产生的应力极小，因此，几乎是一个纯粹的弹性现象，而静态或低频声学试验是不同的热力学现象。从理论上说，静态测量的模量是等温的，但随着频率的升高，动态测量趋近于绝热过程)。但Ef值与Es值相差较大，其平均值比Es约大25%，而Eu值与Es值相差较小，均值约高10%左右。

图7～9分别是静曲模量Es、动态模量Eu以及Ef之间的关系图，并用一元线性回归数学模型对每种模量之间进行回归分析，得到的有关参数及相关系数见表3所示。从图7～9和表3中可以看出，各模量之间均有良好的相关关系，相关系数在0.86～0.94之间，均为0.01水平下显著相关。但Eu与Es之间的相关系数达到了0.94，比Ef与Es以及Eu与Ef之间的相关系数更大，相关性也更好。显然本文方法较直接FFT方法准确度要高很多。

图4 杨木实测信号频谱图

图7 Ef与Es关系图

表1 各差频对应品质因素

表2 杨木试件各种弹性模量值

表3 弹性模量Ef、 Eu、 Es之间回归方程

注：***为0.01水平下显著

5 结 论

提取信号共振基频是声-超声方法测量木材弹性模量的关键，虽然直接FFT提取基频计算动态模量与标准力学方法所测数据有较好的相关性，但数值相差较大，而本文方法无论是相关性或是数值都较直接FFT有明显地改善。

(1)提出了最大公约数算法提取信号基频的方法，并给出了详细的提取步骤。实验表明该算法能够克服FFT方法受噪声干扰和传感器谐振频率所限的影响，能较准确地提取信号基频，从而能更有效地计算木材的动态弹性模量；

(2)应用本文算法对杨木样本进行了测试，计算的弹性模量值与FFT方法相比，误差降低了约10%，同时与静曲弹性模量的相关性也有0.86左右提升到了约0.94，使得动态弹性模量与静曲模量之间的相关性更加显著，从而可更精确有效地预测木材的抗弯模量。

参 考 文 献

[1]刘 妍,张厚江.木质材料力学性能无损检测方法的研究现状与趋势[J].森林工程,2010,26(4):46-49.

LIU Yan,ZHANG Hou-jiang.Research situation and trend on non-destructive testing method of wood material mechanical properties [J].Forest Engineering,2010,26(4):46-49.

[2]Bucur V.An ultrasonic method for measuring the elastic constants of wood increment cores bored from living trees[J].Ultrasonics,1983 (21):116-126.

[3]Da E R,Leite S,Hein P R G,et al.Estimation of the dynamic elastic properties of wood from Copaifera langsdorffii Desf using resonance analysis [J].Cerne,Lavras,2012,18 (1):41-47.

[4]Grabianowski M,Manley B,Walker J C F,Acoustic measureme-nts on standing trees,logs and green lumber[J].Wood Science and Technology,2006(40):205-216.

[6]Kawamoto S,Muehl J H,Williams R S.Use of acousto-ultrasonic techniques to determine properties of remanufactured particleboards made solely from recycled particles[J].Third International Workshop on Green Composites,2005,Kyoto,Japan.

[7]刘镇波,刘一星,于海鹏,等.实木板材的动态弹性模量检测[J].林业科学,2005,41(6):126-131.

LIU Zhen-bo,LIU Yi-xing,YU Hai-peng,et al.Research on the dynamic modulus of elasticity measurement of lumber [J].Scientia Silvae Sinicae,2005,41 (6):126-131.

[8]Ilic J.Relationship among the dynamic and static elastic properties of airdry Eucalyptus delegatensis R.Baker[J].Holz Als Roh Und Werkstoff ,200l,59(3):169-175.

[9]Liang S Q,Fu F.Comparative study on three dynamic modulus of elasticity and static modulus of elasticity for Lodgepole pine lumber [J].Journal of Forestry Research,2007,18(4):309-312.

[10]朱晓冬,王逢瑚,孙建平.单板层积材动态弹性模量的无损检测[J].东北林业大学学报,2008,36(2):30-32.

ZHU Xiao-dong,WANG Feng-hu,SUN Jian-ping.Nondestru-ctive test on the dynamic modulus of elasticity for laminated veneer lumber [J].Journal of Northeast Forestry University,2008,36(2):30-32.

[11]W.T.Thomson 著,康 渊 译.振动学理论及应用[M].北京: 晓园出版社,1994:206-208.

[12]徐 锋,刘云飞.基于中值滤波-奇异值分解的胶合板拉伸声发射信号降噪方法研究[J].振动与冲击,2011,30(12):135-140.

XU Feng,LIU Yun-fei.Research on noise reduction of acoustic emission signals generated from plywood stretching based on median filter-singular value decomposition [J].Journal of Vibration and Shock,2011,30 (12):135-140.

[13]中华人民共和国国家标准:木材抗弯弹性模量试验方法(GB/T1936.2-2009)[M].北京: 中国标准出版社,2009.