地铁隧道钻爆法施工影响下混凝土结构损伤预测方法研究

孟 丹， 朱崇钊

(1.青岛农业大学 建筑工程学院，山东 青岛 266109；2.即墨市建筑工程管理处 质量管理站，山东 即墨 266200)

当前我国城市浅埋暗挖隧道、地铁工程都普遍面临一个重大的技术难题，即隧道下穿城区时，如何确保城市地表的环境安全[1]。而首当其冲的是大量地表建筑物(群)，对于钻爆法施工隧道上方的建筑物，地表变形和爆破振动都会对其产生影响，建筑物变形安全与开裂控制，俨然已经成为下穿工程中的重中之重。国内外针对此问题也展开了大量的研究工作。

在爆破振动的影响方面，陈士海等[2]研究各方向爆破地震波作用下钢筋混凝土建筑沿高度方向的结构响应频谱、能量分布特性及幅值变化规律；李洪涛等[3]研究了建筑物对爆破地震中不同频率能量成分的响应特征；魏海霞等[4]利用动力有限元建模并模拟开裂过程，通过定义结构单元的临界失效状态来寻求典型砌体结构房屋的爆破振动安全标准值；陈士海等[5]建立了混凝土的正交各向异性动态损伤本构关系，结合适用于正交各向异性的Hoffman屈服破坏准实现了爆破振动荷载作用下混凝土结构的开裂预测。总体上看，当前的研究成果侧重于定性的、经验的分析，对建筑物变形开裂的定量研究较少。而只有在量化前提下，才能对建筑物进行较好的变形风险评估。在地表变形的影响方面，易小明等[6]结合厦门机场路隧道下穿建筑群的工程实践，分别采用屈服接近度模型和Mazars 损伤模型，对地表房屋变形开裂进行定量的计算与评估。但是现有的房屋损伤定量评估研究结果是建立在经典强度理论的基础上，此种强度理论的相关参数是针对岩石等特定材料提出的，不适用于混凝土和同类结构材料。

因此，本文根据爆破振速监测数据获得了爆破振动加速度曲线；利用随机介质理论反分析隧道开挖引起的地表移动参数，预测了建筑物下方的地表沉降。在推导了基于混凝土破坏准则的屈服接近度函数的基础上，定量预测了地表沉降和爆破振动影响下建筑结构的损伤状况，以及建筑结构的损伤分布范围和演化过程。

1 工程概况及地表沉降预测

1.1 工程概况

青岛市地铁一期工程(3号线)土建11标万年泉路站～李村站区间全长1 085.65 m ，区间隧道均采用钻爆法施工，穿岩层段采用全断面开挖，靠近李村站穿砂层段采用台阶法开挖，断面形式均为马蹄形。区间从万年泉路站出发，下穿万隆商厦等7栋建筑物后到达李村站。本文的研究对象即为区间下穿的7栋建筑物之一，该建筑物为九层框架结构，与区间隧道的相对位置关系见图1。区间隧道下穿该建筑物里程：左K19+533.5～左K19+590.00，隧道断面尺寸6.35×5.9，围岩等级Ⅵ级。

穿越该建筑物开挖前，对富水砂层采用水泥-水玻璃双浆液进行超前注浆加固地层。开挖时，超前小导管Φ42，长3 m，环纵间距300×1 000 mm，型钢拱架纵向间距为500 mm，250 mm厚喷射混凝土，单层钢筋网8@150×150 mm，每榀型钢拱架8根Φ42、L=3.5 m锁脚锚管，下半断面初喷混凝土100 mm。

图1 建筑物与隧道的相对位置关系

1.2 爆破振动监测结果及分析

钻爆法施工穿越建筑物时，建筑物不仅受到地表沉降的影响，还会受到爆破振动的影响。在实际工程中，这两种作用应该同时作用于建筑结构，甚至爆破地震波对结构的冲击效应更为提前。但是为了简化计算，在研究两种因素的双重影响时，本文采用先对结构施加沉降扰动，然后施加爆破振动激励，据此来分析这两种扰动对建筑结构的影响。

本文选用的爆破振动数据来源于现场监测，14个监测点均布置在建筑物一层靠近基础的位置，根据建筑物的周长沿建筑物周边每隔13m布置一个点，安装速度传感器进行监测，爆破振动监测结果如表1所示。选定9、13和14三个监测点的监测数据，根据这两点的切向速度时程曲线经微分处理得到其加速度时程曲线如图2所示。

表1 爆破振动监测结果

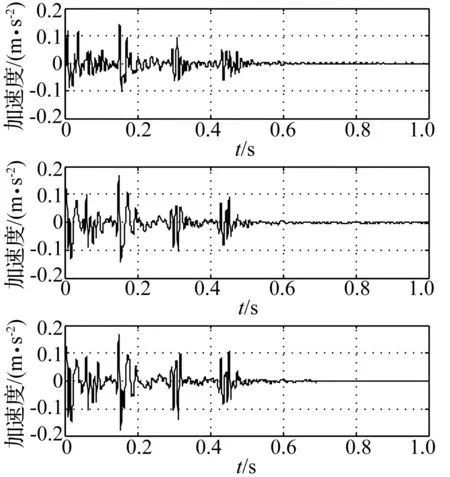
图2 加速度时程曲线

2 混凝土结构损伤预测方法

2.1 屈服接近度函数

周辉等[7]为了研究围岩稳定性问题，针对Mohr-Coulomb准则等古典强度理论推导了屈服接近度的计算函数。具体做法是将问题假定为理想弹塑性问题，假设岩石的强度准则为莫尔-库仑准则或其它屈服准则，根据主应力空间中非屈服应力点和屈服面的关系，在经典塑性理论框架内定义了屈服接近度指标，并建立了相应于不同类型的屈服准则的屈服接近度函数，其中Mohr-Coulomb准则的屈服接近度函数为:

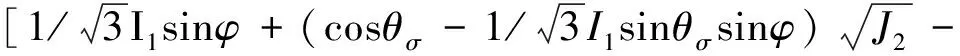
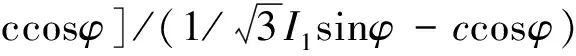
(1)

但是古典的强度理论都是针对某种特定材料提出的。例如，Von Mises准则适用于塑性材料，在金属塑性力学中应用广泛；Mohr-Coulomb准则反映了材料抗拉和抗压强度不等的特点，适用于脆性的土壤、岩石类材料。古典的强度理论包络面的形状过于简单，与复杂的混凝土实际破坏包络面相差很远，从整体上看，古典强度理论不适用于混凝土和同类结构材料。为了解决本文的研究对象混凝土结构的开裂损伤问题，此处引入混凝土材料的破坏准则来建立相应的屈服接近度模型。常用的 Ottosen破坏准则[8]表达式为:

(2)

式中:fc为混凝土材料的单轴抗压强度。根据关系:

(3)

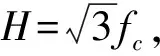
f(σπ,τπ)=

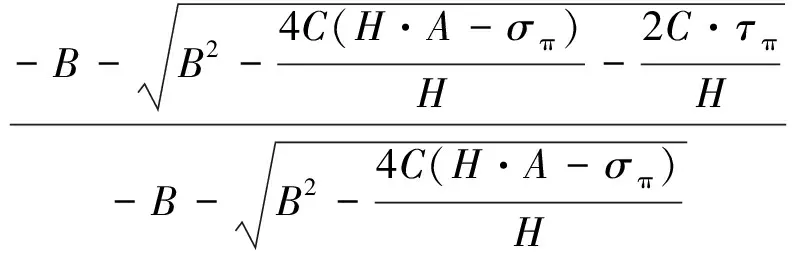
(4)

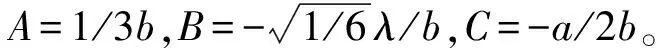
在Ottosen准则中，

该准则中的四个参数分别取值为：a=1.275 9、b=3.196 2、k1=11.736 5、k2=0.980 1。

过-王准则[9]表达式为:

τ0=a[(b-σ0)/(c-σ0)]d

(6)

根据屈服接近度函数的定义可得过-王破坏准则的屈服接近度函数为:

f(σπ,τπ)=

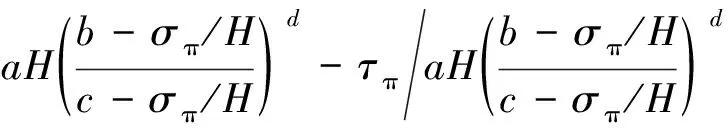
(7)

过-王准则中，

c=ct[cos(1.5θ)]1.5+cc[sin(1.5θ)]2

(8)

该准则中五个参数分别取值为a=6.963 8、bv=0.09、d=0.929 7、ct=12.244 5、cc=7.331 9。

屈服接近度可广义的描述为一点的现时状态与相对最安全状态的参量的比，f∈[0,1]。同时屈服接近度也是一种开裂安全度定义，有分布、演化特征，其力学涵义明确。所以用屈服接近度来定义结构的开裂安全将是合适的。因此，本文将结构开裂损伤安全度定义为:

(9)

2.2 爆破振动损伤结果分析

为了得到基于混凝土破坏准则的屈服接近度损伤模型中的相应主应力和偏应力不变量，本文选取图1中建筑物的一榀框架建立有限元模型，如图3所示。在建立有限元模型的过程中，相关参数均根据现场检测结果确定：① 框架结构层高4.2 m，共 9层；② 构件尺寸：柱截面600×600 mm，梁截面200×400 mm；③ 混凝土材料：梁、柱均采用C35，泊松比δ1=0.2，密度ρ=2 700 kg/m3；④ 构件的配筋量：构件所用钢筋型号均为HRB335，对称配筋，柱配筋率为1.1%，梁配筋率为0.4%。

图3 框架结构有限元模型

对建筑结构输入第三条爆破振动加速度曲线，得到结构在爆破振动影响下的应力分布情况如图4所示。

根据爆破振动作用下结构的应力分布，结合屈服接近度函数式(4)和式(7)便可定量计算结构的损伤分布。图5为第一条和第三条两种爆破振动作用下一层框架梁的损伤分布情况。从图中可以看出由爆破振动产生的应力得到的屈服接近度在0.95～1.0范围内，根据式(9)屈服接近度的定义，爆破振动冲击对建筑结构开裂损伤的影响较小。两条爆破振动曲线的最大振速分别1.63 cm/s和2.79 cm/s，所以本地段现场监测结果显示，在爆破振动影响下混凝土结构不会出现开裂损伤。

图4 爆破振动影响下一层框架梁应力分布曲线

2.3 振动与沉降的叠加影响分析

2.3.1 地表沉降

根据文献[10]，距离开挖工作面较远处，隧道开挖可以认为是一个平面应变问题。另外隧道开挖后即采取支护措施，开挖空间将发生有限变形。假定开挖横断面区域Ω变形后成为ω，将单元dξdη开挖引起的地表下沉在塌陷面积上进行积分，就可获得该情况下隧道上覆地层的位移:

S(x)=SΩ(x)-Sω(x)=

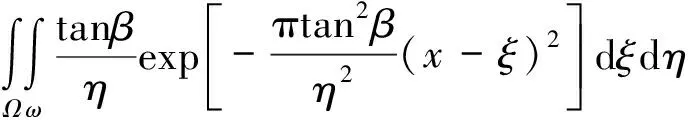
(10)

式中：β为隧道上部地层的主要影响角。

对于双线地铁隧道，两隧道Ⅰ、Ⅱ处于同一水平面上，隧道开挖深度为H，它们的开挖初始半径均为As，两隧道中心距为L(L>As)，隧道建设将引起地表发生移动和变形。设隧道施工完成后隧道Ⅰ和隧道Ⅱ半径收缩值均为ΔAs，总的地表下沉S(x)为开挖隧道Ⅰ所引起的地表下沉SⅠ(x)和开挖隧道Ⅱ所引起的地表下沉SⅡ(x)的线性叠加，即:

S(x)=SⅠ(x)+SⅡ(x)

(11)

(12)

式中：m为地表下沉测点数；x=(tanβ,ΔAs)。

利用反分析的方法来确定地表移动参数，就是寻求一组参数x，使得目标函数值达到极小。本文在优化计算中采用自适应遗传算法，这种算法是一种基于种群层次的优化算法。根据优化算法即可编制成反分析程序进行计算。

为了得到建筑物下方在隧道开挖影响下的地表沉降量，本文选取5个断面进行地表移动参数反分析[11]，最终得到的反分析结果为tan(β)=0.86,ΔAs=19.8 mm。

利用上述反分析结果对建筑物下方隧道开挖引起的地表沉降进行预测，结果见图6(H=13.4 m，L=17.0 m)。其中，曲线1为根据反分析参数预测的地表沉降曲线。

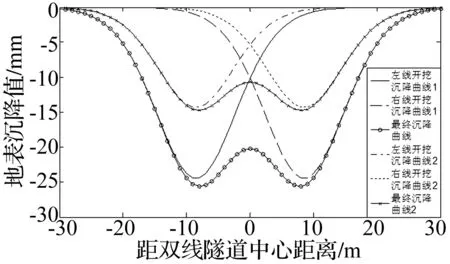
图6 隧道断面不同开挖阶段地表沉降预测曲线

双线隧道开挖完成后，地表沉降曲线如图6中的马鞍形的最终沉降曲线。将此沉降值作为边界条件施加于该模型，根据所得主应力计算的屈服接近度如图7所示。

从图7的损伤结果分析可以看出，当该混凝土结构在隧道开挖的预测地表沉降的影响下会有若干个区域开裂破坏。因此，为了进一步研究的需要，调整地层变形参数，改变地表沉降的范围和大小，预测的地表沉降情况如图6中曲线2所示。根据参数调整后沉降预测结果，控制地表沉降最大值为15 mm，结构一层梁的应力分布情况、一层和顶层的损伤破坏情况如图8所示。

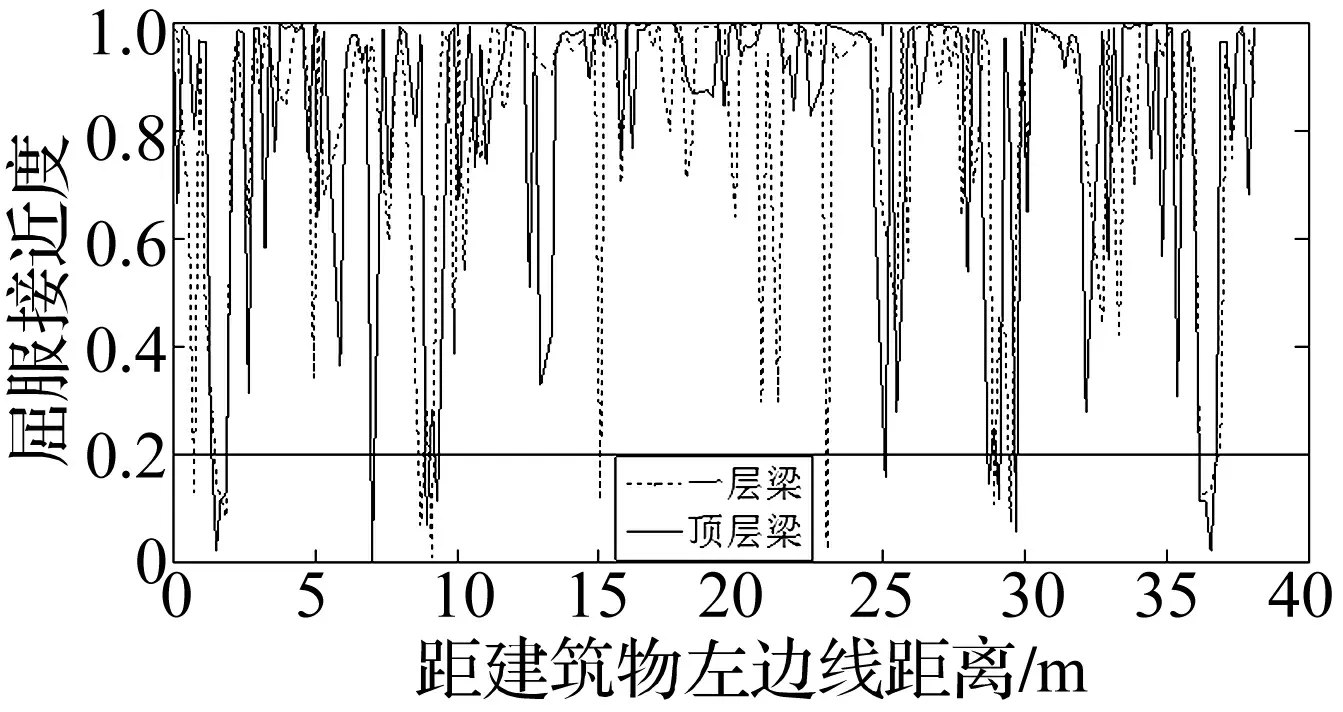
图7 最终沉降框架梁屈服接近度分布曲线

从图8中可以看出，在该地表沉降的影响下，结构屈服接近度的最小值在0.35左右，不会发生开裂损伤破坏。结合图7的结构损伤情况，以及图6的地表沉降情况，本文认为将地表沉降最大值控制在15～20 mm范围内，建筑物不会出现过多区域的开裂损伤。

图8 沉降控制

2.3.2 叠加影响分析

由于钻爆法施工隧道穿越的建筑物会同时受到地表沉降和爆破振动冲击的影响。因此，本节首先给建筑结构施加最大值为15 mm的沉降，然后再将上述第三条爆破振动加速度时程曲线输入到变形后的结构，分析其两种效应叠加作用下的开裂损伤情况。图9为一层框架梁的应力分布情况、一层和顶层梁的开裂损伤分布情况。比较图8和图9可以看出，建筑结构在地表沉降的作用下和在两种效应的同时作用下应力分布和开裂损伤分布没有明显的变化，也就是爆破振动对建筑结构的开裂损伤贡献较小。

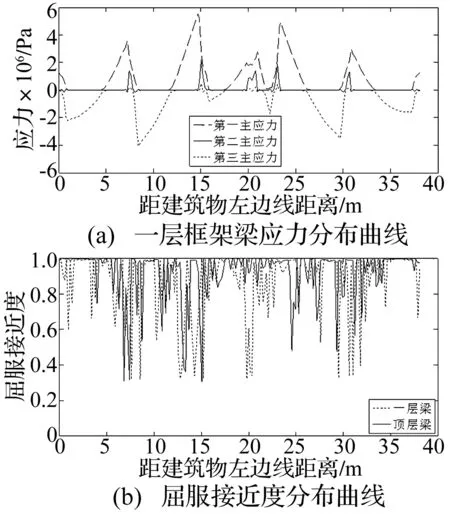
图9 叠加影响

3 结 论

本文在综合分析爆破振动和地表沉降影响下建筑结构损伤分布和演化过程的基础上，得到了以下结论：

(1)通过屈服接近度模型，实现了地表建筑物开裂损伤的量化评估；

(2)钻爆法施工诱发地震的主频率，比常见建筑物的固有频率相对要高，当主振频率的这部分能量作用于建筑物时，会被很大程度的削弱，只有爆破振动中延伸到建筑物固有频率范围以内的能量才会对建筑物产生影响。因此，建筑物的损伤及其演化过程中爆破振动的贡献较小。

参 考 文 献

[1]王梦恕.地下工程浅埋暗挖技术通论[M].合肥：安徽教育出版社，2004.

[2]陈士海，魏海霞，张子华，等.钢筋混凝土结构爆破地震响应频谱及幅值变化规律分析[J].振动与冲击，2011，30(1)：213-217.

CHEN Shi-hai，WEI Hai-xia，ZHANG Zi-hua，et al.Spectral analysis and amplitude varying for blasting vibration response of a reinforced concrete building[J].Journal of Vibration and Shock，2011，30(1)：213-217.

[3]李洪涛，舒大强，卢文波，等.建筑物对爆破振动中不同频率能量成分的响应特征[J].振动与冲击，2010，29(2)：154-158.

LI Hong-tao，SHU Da-qiang，LU Wen-bo，et al.Response characteristics of a structure to different frequency components in blasting vibration energy[J].Journal of Vibration and Shock，2010，29(2)：154-158.

[4]魏海霞，陈士海，张安康.基于动力有限元方法的典型砌体结构爆破振动安全标准的探讨[J].振动与冲击，2011，30(5)：49-53.

WEI Hai-xia，CHEN Shi-hai， ZHANG An-kang.Safety standards discussion for blasting vibration of typical masonry buildings with dynamic finite element method[J].Journal of Vibration and Shock，2011，30(5)：49-53.

[5]陈士海，张安康，杜荣强，等.混凝土正交各向异性动态损伤本构模型研究[J].振动与冲击，2012，31(3)：23-26.

CHEN Shi-hai， ZHANG An-kang，DU Rong-qiang，et al.Orthotropic dynamic damage constitutive model for concrete[J].Journal of Vibration and Shock，2012，31(3)：23-26.

[6]易小明，张顶立，李鹏飞.隧道下穿时地表房屋变形开裂的定量评估[J].岩石力学与工程学报，2008，27(11)：2288-2294.

YI Xiao-ming，ZHANG Ding-li，LI Peng-fei.Quantitative evaluation of house deformation and cracks caused by tunnel-crossing[J].Chinese Journal of Rock Mechanics and Engineering，2008，27(11)：2288-2294.

[7]周 辉，张传庆，冯夏庭，等.隧道及地下工程围岩的屈服接近度分析[J].岩石力学与工程学报，2005，24(17)：3083-3087.

ZHOU Hui，ZHANG Chuan-qing，FENG Xia-ting，et al.Analysis of rock mass stability in tunnel and underground engineering based on yield approach index[J].Chinese Journal of Rock Mechanics and Engineering，2005，24(17)：3083-3087.

[8]Ottosen N S.A failure criterion for concrete[J].Journal of the Engineering Mechanics Division，1977，103(4)：527-535.

[9]过镇海，时旭东.钢筋混凝土原理和分析[M].北京：清华大学出版社，2003.

[10]阳军生，刘宝琛．城市隧道施工引起的地表移动及变形[M].北京：中国铁道出版社，2002.

[11]孟 丹，臧晓光，于广明，等.地铁车站开挖引起地表沉降分析方法的对比研究[J].岩石力学与工程学报，2012，31(6)：1169-1177.

MENG Dan，ZANG Xiao-guang，YU Guang-ming，et al.Comparative study of analytical methods for ground surface settlement induced by subway station construction[J].Chinese Journal of Rock Mechanics and Engineering，2012，31(6)：1169-1177.