基于谱有限元的自由阻尼梁结构损耗因子分析

尹帮辉， 王敏庆

(西北工业大学 航海学院，西安 710072)

振动噪声对设备的安全性及可靠性具有很大的危害，受到广泛的关注。自由阻尼处理[1]是一种在振动表面附加黏弹阻尼材料，通过阻尼材料的振动将机械能转化为热能从而达到抑振降噪目的的阻尼处理方法，该方法广泛用于潜艇消声瓦的设计。结构损耗因子[2]用于描述结构振动时的耗能特性，常用作阻尼处理的评价参数，因此准确的获取结构损耗因子对于振动噪声控制具有重要意义。本文使用谱有限元法[3-5]对自由阻尼梁的结构损耗因子进行研究。

为了能够有效吸声，潜艇消声瓦越做越厚，阻尼层的振动变形不再单纯是弯曲变形，剪切变形以及垂直于中性面的拉伸变形都不容忽略，自由阻尼结构损耗因子计算的经典公式[1]不再适用，必须寻找新的计算方法。谱有限元法[3-5]是一种使用有限元来分析无限介质中波传播特性的方法，对于多层板，Shorter[4]从拉格朗日原理出发，对多层板中各阶波的波数和波形推导了谱有限元计算公式，然后根据谱有限元法得到的特征波形使用应变能法得到各阶波的损耗因子。文献[3-5]主要讨论了阻尼结构中存在的波的类型及其损耗因子，而对激励类型以及边界反射对结构损耗因子的影响没有涉及。载荷所能激励起的波类型在很大程度上决定了结构损耗因子大小，阻尼结构在不同类型或者不同方向的载荷作用下将激励起不同种类的波分量，因而其结构损耗因子也各不相同。另一方面，如果振动系统的尺寸较小、激励点位置靠近边界或者边界条件发生改变，那么边界处的反射波将使振动系统的应变能分布产生较大变化，这将导致结构损耗因子发生一定的改变。所以关于激励类型和边界反射对结构损耗因子影响的分析具有重要的意义。

本文首先使用谱有限元分析了自由阻尼梁中扩散波类型及其损耗因子，通过对其特征波形的分析探讨了各个频率下每种波的激励条件，然后使用有限元对自由阻尼长梁做谐响应分析得到各个单元的应变能，根据应变能法计算得到该长梁分别在垂直和水平激励下的结构损耗因子，对结构损耗因子同激励起的波类型之间的关系进行了讨论，最后分析了边界反射对结构损耗因子的影响。本文通过对自由阻尼梁结构损耗因子同激励类型与边界反射的关系的探讨，揭示了自由阻尼结构阻尼大小的影响因素，为潜艇消声瓦等自由阻尼结构的设计提供一定的帮助。

1 基本理论

1.1 谱有限元法

谱有限元法[3-5]是一种分析无限介质中波传播特性的有限元方法，它使用直线单元的线性形函数对位移场进行离散，将离散形式的位移场代入拉格朗日原理得到特征方程，对特征方程进行求解得到某频率下的各阶波的特征波数和特征波形。Shorter[4]推导了多层板中的谱有限元公式，本文参考其方法推导了平面应力状态下的自由阻尼梁的谱有限元公式。

设一列平面波向着梁的正方向即x轴正向传播，如图1所示

图1 自由阻尼梁中的波传递

则其位移场可表示为:

d(x,y,t)=[u(y)v(y)]Tei(ωt-kx)=

d(y)ei(ωt-kx)

(1)

其中:u(y)、v(y)分别为x方向和y方向位移。使用线性函数作为形函数对位移场进行离散，可得:

d(y)=[u(y)v(y)]T=[INiINj][uiviujvj]

(2)

其中:I为2×2的单位矩阵，Ni、Nj为形函数，可以表示为:

(3)

其中:yi、yj为线单元的两节点的坐标。使用矩阵和向量符号，可将式(2)表示为:

d(y)=Nq0

(4)

其中:N=[INiINj]为形函数矩阵，q0=[uiviujvj]T为节点位移向量。对于基底层划分m个单元，阻尼层划分n个单元，其单元、节点划分示意图如图2所示。

图2 谱有限元单元、节点划分示意图

对于保守系统，其拉格朗日原理为:

(5)

将式(2)代入式(5)可得到该保守系统的振动需满足下列最优化问题:

(6)

式中:K、M分别为总体刚度矩阵和总体质量矩阵，其定义参考文献[4]，ω为角频率。式(6)可化为下列特征方程:

(K-ω2M)q0=0

(7)

式中，M为常矩阵，K中含有波数k，所以在某一特定频率ω下，该式经过整理可化为关于波数以及波形的特征值问题[4]，对其进行求解可以得到该频率下各阶波的特征波数和特征波形。

1.2 有限元法

有限元法将连续的求解域离散为一组单元的组合体，用在每个单元内假设的近似函数来分片的表示求解域上待求的未知场函数，近似函数通常由未知场函数及其导数在单元各节点的数值插值函数来表达，从而使一个连续的无限自由度问题变成离散的有限自由度问题。本文使用通用有限元分析软件ANSYS对自由阻尼梁做谐响应分析，通过后处理得到每个单元的应变能，然后使用应变能法计算得到自由阻尼梁的结构损耗因子。

振动系统的运动方程可以写为:

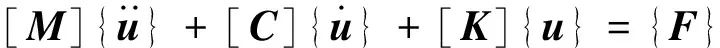
(8)

式中:[M]、[C]、[K]分别为总体质量矩阵、总体阻尼矩阵、总体刚度矩阵，{u}、{F}分别为位移向量和载荷向量。对于简谐激励，设[F]=[F0]eiωt，式(8)可化为:

[Kc]{uc}={Fc}

(9)

式中:下标“c”表示该矩阵或向量为复的。对上式使用波前求解法可得到各节点的位移响应，具体参考ANSYS理论手册。根据各节点的位移可以计算各单元应力和应变，进而可得到单元应变能。

1.3 应变能法

应变能法是一种根据统计能量分析关于内损耗因子定义[6-8]，利用振动系统振动时一周期时间内耗能总和同应变能总和的比值来计算结构损耗因子的方法，即:

(10)

式中:η、Ei为第i层材料的材料损耗因子和应变能。该方法广泛用于多层板结构损耗因子的计算。

由式(7)得到给定频率下各阶波的特征波数及特征波形，根据特征波形计算出该波传递时各层材料的时间平均应变能，进而由应变能法可以计算出第k阶波的损耗因子[4]:

(11)

式中:ηn为第n层材料的材料损耗因子，Pk为第k阶波的特征波形，K(n)为第n层材料的刚度矩阵，K为总体刚度矩阵。本文称这种应变能法为“波应变能法”。

当结构在一般简谐载荷激励时，通常会同时激起几种波，这时上述波应变能法不再适用[9]，本文使用有限元谐响应分析得到的各层材料的应变能计算结果来计算其结构损耗因子，即:

(12)

式中:N为层数，ηi为第i层材料的材料损耗因子，Ni为第i层材料所含单元数，Eij为第i层材料的第j个单元的应变能。本文称这种方法为“一般简谐激励下的应变能法”。

2 激励类型对结构损耗因子的影响

当自由阻尼梁受到简谐激励激振时，其振动响应主要为各阶扩散波(propagating waves)的叠加，只有激励点附近很小的区域受耗散波(evanescent waves)的影响，因此本文主要考虑扩散波对结构损耗因子的影响。谱有限元一般计算量不大，本文使用MATLAB按照第1节公式编写程序，对下列自由阻尼梁进行分析：基底层厚度10 mm，杨氏模量2×1011Pa，泊松比0.3，密度7 800 kg/m3；阻尼层厚40 mm，杨氏模量2×107Pa，泊松比0.4，密度1 000 kg/m3。基底层划分为6个单元，阻尼层划分为48个单元。

经过谱有限元分析得到的自由阻尼梁的频散曲线的实部和虚部如图3和图4所示，其中波数为纯实数的波为扩散波。图3中的“纵1”、“纵2”、“纵3”、“弯1”、“弯2”为5种扩散波，前面的“纵”表示纵波，“弯”表示弯曲波，后面的数字表示阶数，例如“弯2”表示第2阶弯曲波。这里的弯曲波和纵波是根据特征波形位移分量的主要成分以及图3的频散曲线的连续性进行区分的，和经典教材[10]中的弯曲波和纵波不完全一致，当位移主要为x方向的分量时称为纵波，而当位移主要为y方向分量时称为弯曲波。从图3可以看出：频率越高，扩散波的类型越多；纵波的波数一般远小于弯曲波的波数。

本文使用结构损耗因子同阻尼层材料损耗因子的比对结构损耗因子进行无量纲化，称之为“损耗因子比”，即:

(13)

其中:ηs为结构损耗因子，ηd为阻尼层材料损耗因子。对于各阶扩散波，通过谱有限元计算得到其特征波形，根据波应变能法即式(11)得到各阶波的损耗因子。对应于图3中的各阶扩散波的损耗因子比如图5所示。

下面选择一些典型频率，使用谱有限元分析其各阶波的激励条件，其谱有限元计算结果如表1所示，其中波形分类是根据各阶波的特征波形进行的分类，下文将进行详细讨论，激励条件根据波形分类进行确定。从该表中可以看出：垂直激励主要激励起最高阶弯曲波或者某些低阶纵波，水平激励主要激励起最高阶纵波。这里阶数的高低是由该波产生的起始频率决定的，频率越高产生的波的阶数越高，如图3所示。

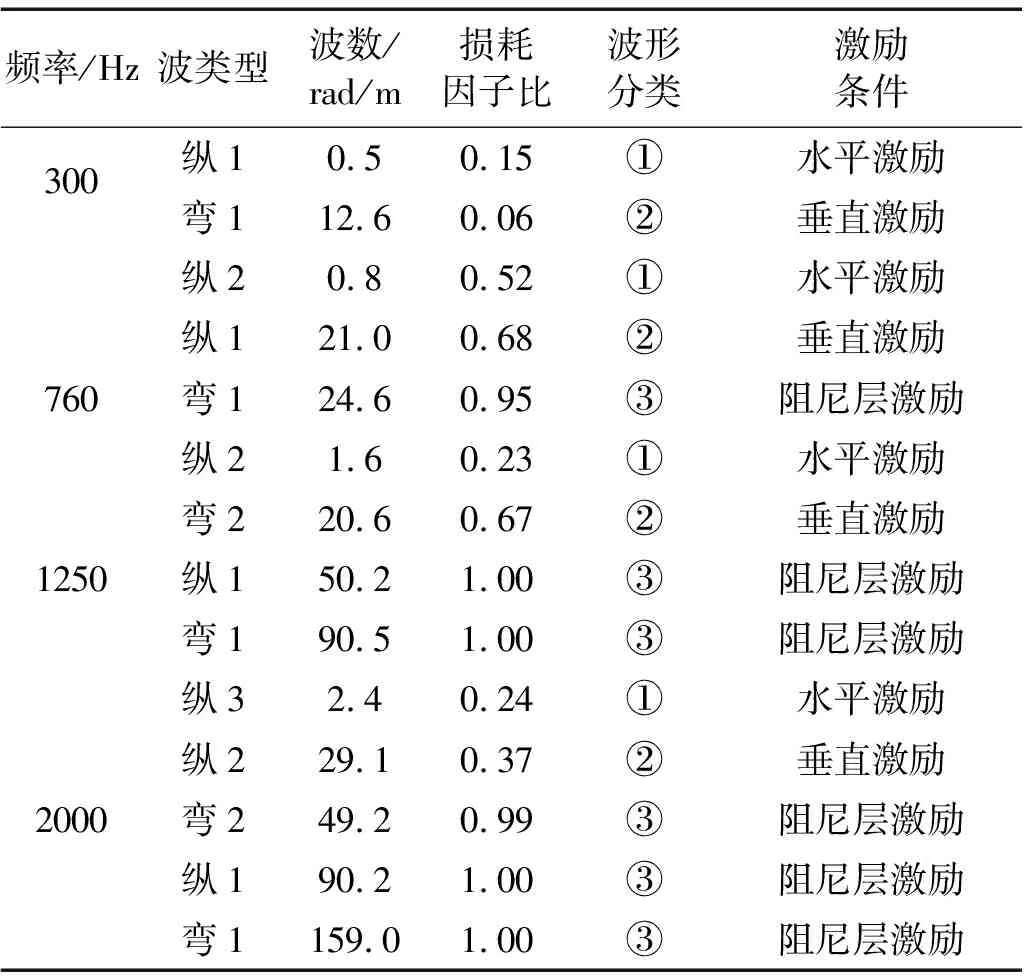
表1 各个频率下的扩散波的损耗因子比和激励条件分析

图6 各个频率下的扩散波的波形

对应于表1的一些波的特征波形如图6所示，该图的横坐标表示距离基底外表面的距离，即图1中的y坐标，纵坐标表示x=0的直线上各节点的x方向和y方向的振动位移。

根据各阶扩散波的波形(一些典型波形如图6所示)，可将表1中的各阶波按照特征波形分为三类：①x方向位移占主导的波形，包括：300 Hz纵1、760 Hz纵2、1 250 Hz纵2、2 000 Hz纵3；②y方向位移占主导的波形，包括：300 Hz弯1、760 Hz纵1、1 250 Hz弯2、2 000 Hz纵2；③基底位移很小的波形，包括：760 Hz弯1、1 250 Hz纵1、1 250 Hz弯1、2 000 Hz弯2、2 000 Hz纵1、2 000 Hz弯1。在第①类和第②类波形中其某一方向的位移占主导，并且基底层上该方向的位移也比较大，所以这两类波容易被基底层上的该方向的简谐激励所激发。第③类波形的位移主要集中在阻尼层内，而基底层上的位移非常小，所以这类波仅能受作用于阻尼层上的载荷所激发，而较难受基底层上的载荷所激发，其结构损耗因子基本上等于阻尼层的材料损耗因子。

表2 对应300 Hz弯1特征波形前4个节点的振动位移

特征波形x方向位移和y方向振动都是复数，对应“300 Hz弯1”的特征波形前4个节点的位移如表2所示，从中可以看出：x方向位移和y方向位移幅角相差90°，这表示当x方向的位移达到峰值的时候，y方向位移达到最小，反之当y方向的位移达到峰值的时候,x方向位移达到最小。图6的各图中的“x方向位移”和“y方向位移”，如果前者的实部数据非0，那么前者绘制的是实部数据，后者绘制的是虚部数据，反之，如果前者的虚部数据非0，那么前者绘制的是虚部数据，后者绘制的是实部数据。

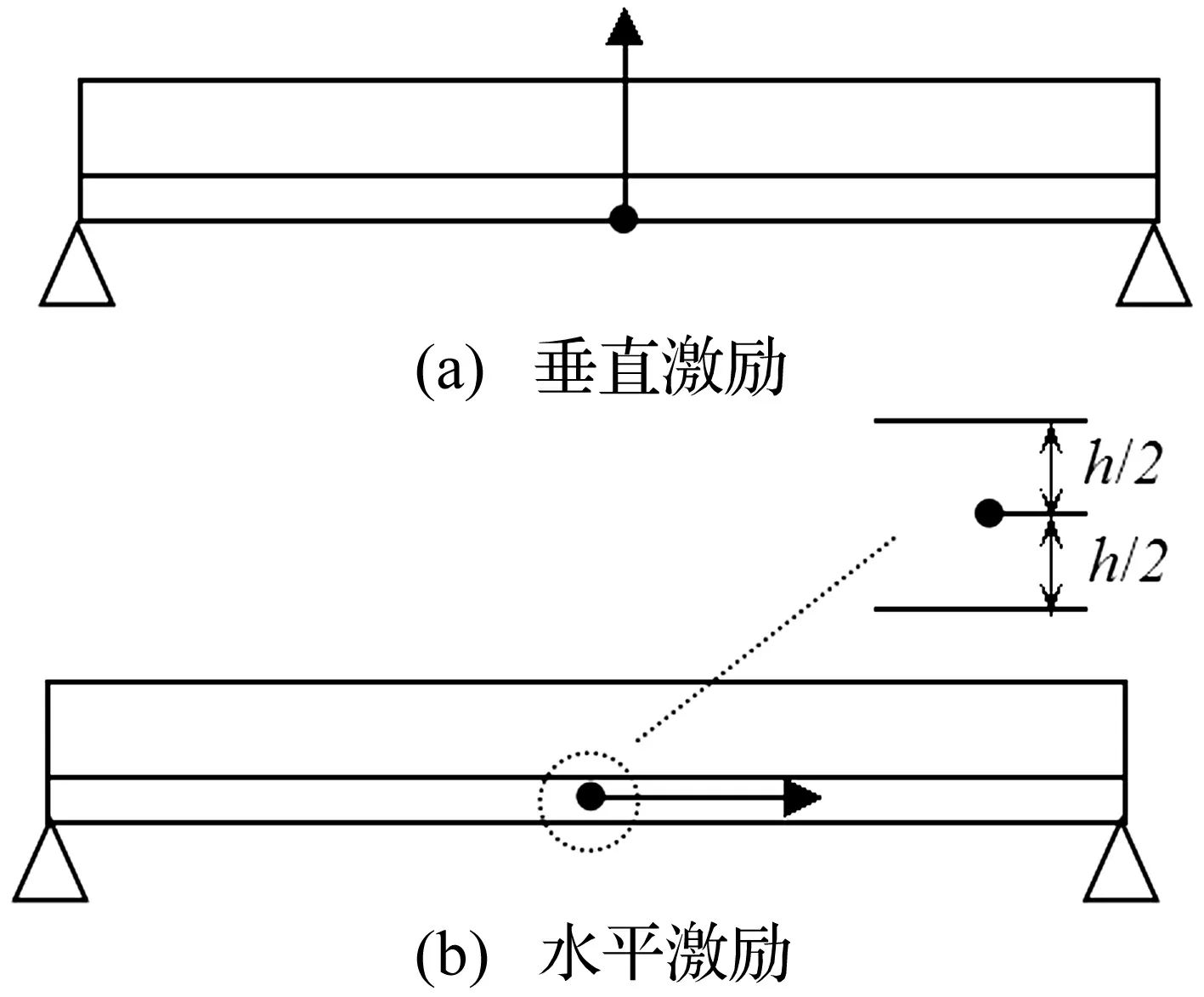
图7 激励点位置和方向

下面使用一般简谐激励下的应变能法研究自由阻尼梁分别在垂直于梁方向和平行于梁方向的简谐激励下的结构损耗因子， 对结构损耗因子同激励起的波类型之间的关系进行讨论，其应变能数据来自于ANSYS谐响应分析。为了能够忽略边界反射波对结构损耗因子的影响，这里梁取得较长，垂直激励时为10 m，水平激励时频率小于500 Hz为25 m，反之为10 m，忽略基底层阻尼，阻尼层的材料损耗因子取为0.1，梁的其他参数同第2节。梁两端简支，激励点位于梁长度方向的中点，垂直激励时位于下端面，水平激励时位于基底板的中性面上，其示意图如图7所示。使用ANSYS的PLANE42单元对梁进行建模，其KEYOPT(3)取3，表示平面应力状态，谐响应分析使用FULL方法。水平激励在低频时的梁取得很长的原因是为了能够忽略边界反射对结构损耗因子的影响。另外， 水平激励时激励点位置选择在基底层的中性面上的原因是为了使水平方向的简谐激励主要激励起纵波，如果作用点选在基底层的下表面，那么由于弯矩的作用使得自由阻尼梁中也会产生较大的弯曲波成分。

上述两种简谐激励下的损耗因子比的结果如图8所示，从中可以看出：当不考虑边界反射时，两种激励下长梁的结构损耗因子同谱有限元分析结果(表1)中该种激励所激励起的波的损耗因子接近。

图8 垂直激励和水平激励下的损耗因子比

3 边界反射对结构损耗因子的影响

载荷所能激励起的波类型在很大程度上决定了结构损耗因子大小，但是如果振动系统的尺寸较小或者激励点位置靠近边界，那么边界处的反射波将使振动系统的应变能分布产生较大变化，这将导致结构损耗因子发生改变，所以有必要研究边界反射对结构损耗因子的影响，本节使用一般简谐激励下的应变能法来研究由于梁长度、激励点位置以及边界条件所引起的边界反射对结构损耗因子的影响，其应变能数据来源于ANSYS谐响应分析。

首先研究梁长度、激励点位置对垂直激励下的梁的结构损耗因子的影响，考虑三种梁：①两端存在边界反射的梁(梁长3 m，激励点位于梁长中点)，②一端边界反射可忽略的梁(梁长10 m，激励点距离一端为梁长的1/20)，③可忽略边界反射的梁(梁长10 m，激励点位于梁长中点)。图9给出了以上三种情况下的损耗因子比，从中可以看出：②和③在大多数频率都较为接近，在一些频率存在较小差异；①和③在一些频率差别较明显。

然后研究边界条件对结构损耗因子的影响，图10为三种不同边界条件下的3m长的自由阻尼梁在中点受到垂直激励时的结构损耗因子随频率变化曲线，从中可以看出：不同边界条件的结构损耗因子一般情况下比较接近，但是在一些频率处会存在较大差异。

图11给出了两端存在边界反射的梁，即图9的情况①，在1 420 Hz的激振力下的位移响应的实部和虚部，在靠近边界的地方可以看到比较明显的反射波，正是由于反射波的存在导致了图9中①和③的损耗因子比的差异。

图11 激励频率为1 420 Hz时的ANSYS振动位移

上述关于边界反射的结论对于水平激励也成立，只是由于纵波波长比弯曲波波长大很多，所以其受边界反射的影响要大得多。

综合2、3节的讨论可以看出：自由阻尼梁的结构损耗因子主要由激励所能激励起的波类型所决定，在一定程度上受到边界反射影响。

4 结 论

(1)垂直激励主要激励起最高阶弯曲波或者某些低阶纵波，水平激励主要激励起最高阶纵波；

(2)梁越长，激励点离边界越远，边界反射对结构损耗因子影响越小；

(3)不同边界条件的结构损耗因子一般情况下比较接近，但是在一些频率点会存在较大差异；

(4)自由阻尼梁的结构损耗因子主要由激励所能激励起的波类型所决定，在一定程度上受到边界反射影响。

参 考 文 献

[1]戴德沛.阻尼减振降噪技术[M].西安: 西安交通大学出版社,1986.

[2]Lyon R H.Statistical energy analysis of dynamical system: theory and application[M].The MIT Press,Cambridge,Massachusetts,1975.

[3]Gavric L.Computation of propagative waves in free rail using a finite element technique[J].Journal of Sound and Vibration,1995,185(3): 531-543.

[4]Shorter P J.Wave propagation and damping in linear viscoelastic laminates[J].Journal of Acoustical Society of America,2004,115(5): 1917-1925.

[5]Finnvede S.Spectral finite element analysis of the vibration of straight fluid-filled pipes with flanges[J].Journal of Sound and Vibration,1997,199(1): 125-154 .

[6]Ungar E E,Kerwin E M.Loss factor of viscoelastic systems in term of energy concept[J].Journal of Acoustical Society of America,1962,34(7): 954-957.

[7]Wilson C J,Carnevali P,Morris R B,et al.Viscoelastic damping calculations using a p-type finite element code[J].Journal of Apply Mechanics,1992,59(1): 696-700.

[8]张少辉,陈花铃.共固化复合材料粘弹阻尼结构的损耗因子研究[J].航空材料学报,2005,25(1): 53-57.

ZHANG Shao-hui,CHEN Hua-lin.Damping analysis of cocured composites with interleaved viscoelastic layers[J].Journal of Aeronautical Materials,2005,25(1): 53-57.

[9]潘利剑,张博明,戴福洪.简谐激励下共固化复合结构粘弹阻尼材料的损耗因子研究[J].振动与冲击,2008,27(2): 57-60,175-176.

PAN Li-jian,ZHANG Bo-ming,DAI Fu-hong.Study on loss factor of cocured composites with an interleaved viscoelastic damping layer under a harmonic excitation[J].Journal of Vibration and Shock,2008,27(2): 57-60,175-176.

[10]Cremer L,Heckl M,Ungar E E.Structure-Borne Sound[M].Springer-Verlag,2005