只利用旋臂旋转运动的起重机消摆控制

欧阳慧珉， 内山直树， 佐野滋则， 张广明， 王德明， 梅 磊

(1.南京工业大学 自动化与电气工程学院,南京 211816；2.日本丰桥技术科学大学 机械工程系,丰桥 441-8580 日本)

起重机系统被广泛地应用于各种场所，例如建筑工地，港湾，以及卡车的载物台等。可是，起重机旋臂的旋转运动会使荷载产生一个二维摆角；因此，操作人员必须具备很高的熟练度来控制起重机使得荷载迅速而准确地到达指定位置。操作上的失误会造成事故，人员伤亡以及破坏周围的环境[1]。

旋转起重机的运动主要分为两方面:① 通过改变悬绳的长度实现荷载的上升和下降；② 旋臂的起伏运动和旋转运动。由于在第一个运动模式中不会产生荷载的摆动现象，因此，对于操作人员来说比较易于控制。然而，对于第二个运动模式就需要进行消摆控制从而增加了操作难度。

为了减轻操作人员的负担和提高他们工作的安全性，许多研究人员已经为起重机系统开发了各种各样的控制方式。Terashima和沈滢等提出了一种基于坐标变换的旋转起重机直线搬送最优控制方法[2-3]。此外还包括滑模控制[4-5]，自适应控制[6]，逆推控制[7]以及基于李亚普诺夫稳定性定理的非线性控制[8]。

然而，在现存的研究中大多同时利用旋臂的起伏运动和旋转运动来实现消摆控制。如果可以提出一种只利用旋臂的旋转运动即无需其起伏运动而实现消摆控制方法的话，就可以实现无需控制旋臂起伏运动的执行机构的起重机，从而大大地简化其结构和降低其制造成本。因为旋臂的起伏运动只是用来克服重力的。

但是，当只利用旋臂的旋转运动来消除这个二维摆角时，起重机在目标位置附近的线性化系统则变成不可控制系统。为了解决这个问题，已经有研究者提出了一些方法。一种是可以抑制荷载摆动而无需摆角信息的轨道生成法[9-10]。但是，这种开环控制方式缺少对于外部干扰的鲁棒性，因此很难应用于实际工程中。另一种是利用由传感器系统测量到的摆角信息实现消摆控制方式。Nakanozo等[11]提出了一种基于神经网络的控制方式，但是只有仿真结果。Kondo等[12]提出了一种两模式切换控制方式:当旋臂到达目标位置附近时，在第一个控制模式中，控制器先减少不可控方向的摆角。在第二个控制模式中控制器再减少可控方向的摆角并且同时控制旋臂的定位。但是，当一个很小的外部干扰增大了不可控方向的摆角时，该方法很难获得良好的控制性能甚至会造成系统的不稳定。

因此，本文将提出一种只利用旋臂旋转运动就可以抑制二维荷载摆角的非线性控制器。由于所设计的控制系统对于如关节间摩擦，荷载质量等参数的变化必需具有鲁棒性，因此首先提出一个基于干扰观测器以及起重机部分线性模型的控制系统。该设计提供了包含产生摆角的离心力项的简单动力学模型。其次，根据李亚普诺夫稳定性定理提出一个非线性消摆控制器。该设计可以实现旋臂对于任意轨道的跟踪控制并同时抑制二维摆角。最后，比较数值仿真和实验结果验证该方法的有效性。

1 旋转起重机模型

在如图1所示的旋转起重机模型中，θ1,θ2分别表示旋臂起伏运动平面的摆角和旋转运动平面的切线方向的摆角；θ3,θ4分别表示旋臂的起伏角和旋转角；L,l分别表示旋臂长度和悬绳长度；x,y,z表示荷载的三维空间位置。

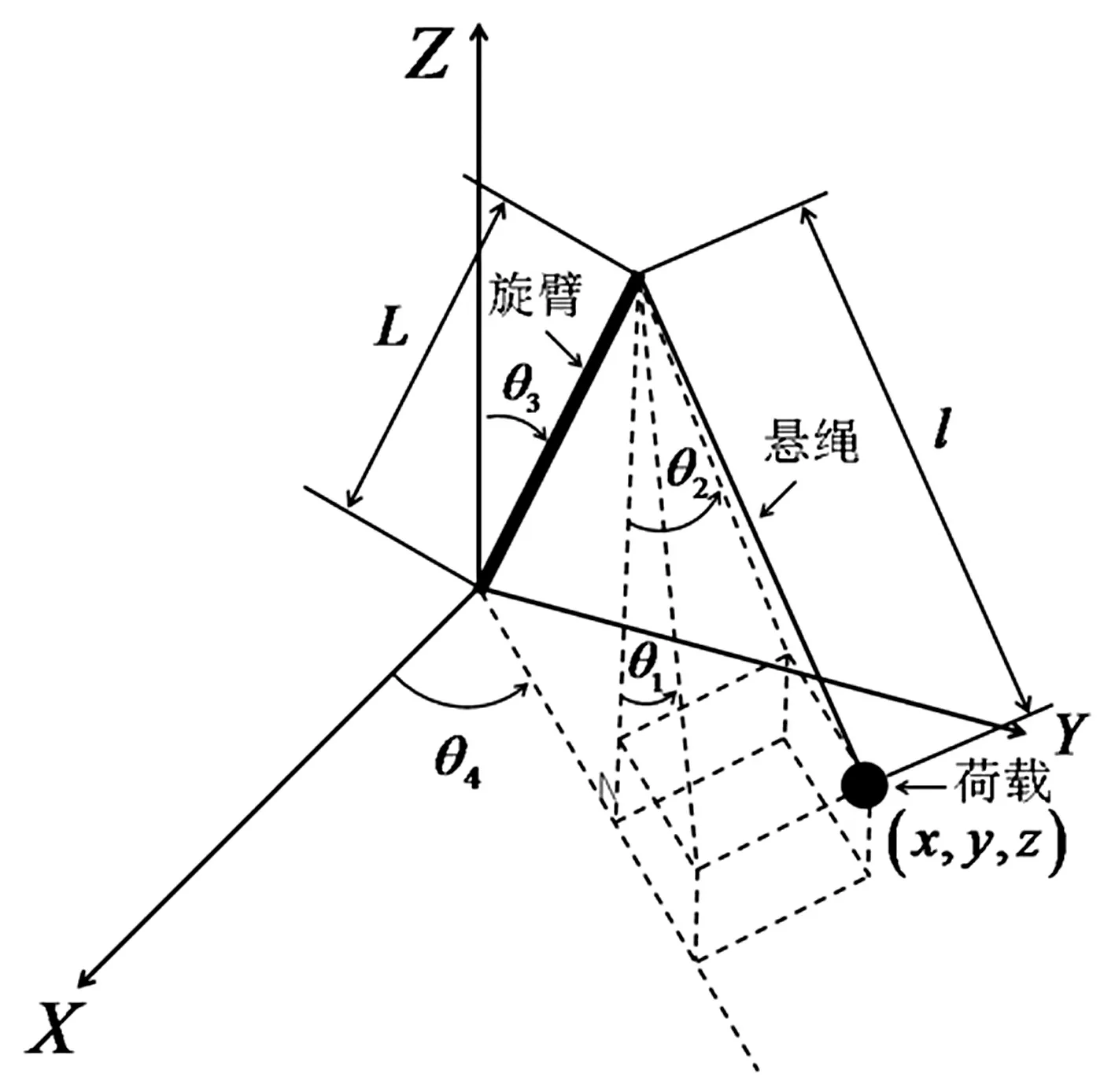
图1 旋转起重机模型

假设旋转起重机模型具有以下特性：

(1)荷载可以看作是一个质点，且悬绳的扭力可以忽略不计。

(2)旋臂的起伏角和旋转角以及它们的角速度；两个方向的摆角以及它们的角速度都可测量。

(3)由于摆角θi很小，因此sinθi≃θi和cosθi≃1(i≃1,2)成立。

旋臂的旋转运动可由下式表示：

(1)

式中:J,d,K,u分别表示旋臂转动惯量，包含非线性力的系统外部干扰，系统参数以及指令电压。式(1)假设旋臂转动惯量J是常量，但是其变化部分可看作系统外部干扰并包含于d。

为了补偿系统外部干扰的影响，将以下所示干扰观测器(DOB)应用于式(1)：

(2)

式中:s,v,ω分别表示微分算子，由反馈控制器算出的新的控制输入以及低通滤波器(LPF)的截止角频率。该控制系统的方框图如图2所示。起重机系统动力学特性在低频区域可表示为下式：

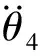
(3)

图2 含有干扰观测器控制系统

另一方面，根据拉格朗日运动方程悬绳和荷载组成的振动系统的动力学方程可由下式表示：

(4)

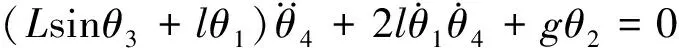
(5)

式中:g表示重力加速度。

(6)

(7)

结合式(3)，式(6)和式(7)，得到以下简易模型：

(8)

(9)

式中:a=g/l,b=Lsinθ3/l。

2 控制器设计和稳定性解析

2.1 控制器设计

(10)

式中:Ke,Kθ1,Kθ2,λ,λ1,λ2都是正常数。式(10)的时间微分为：

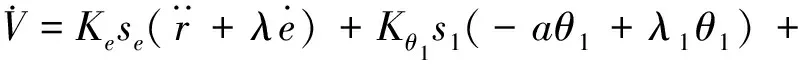
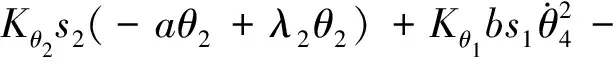
(Kese+Kθ2bs2)v

(11)

根据李雅普诺夫稳定性定理，提出如下所示的控制律：

(12)

p=Kese+Kθ2bs2

Kθ2s2(-aθ2+λ2θ2)

式中:K1,K2是控制器增益，ε是调节控制性能和系统抖振之间平衡点的微小正实数。

2.2 稳定性解析

本节将分析该控制系统的稳定性。当|p|≥ε时，由式(11)和式(12)可得：

(13)

(14)

从式(14)得到以下关系：

α=2K1·min{Ke,Kθ2b2}

(15)

另外，此变结构控制器对式(4)和式(5)中忽略的非线性项也具有鲁棒性。

3 仿真与实验

3.1 目标轨道

为了验证本文中新方法的有效性，使用如下所示初始和最终位置的加速度都为零且广泛地应用于各种工业场合的摆线作为旋转角的目标轨道。

(16)

式中:θ0,θ4f,ts,tf分别表示初始角度，最终角度，到达时间以及终了时间。在本文中，各参数分别设定为θ0=0°,θ4f=45°,ts=3 s,tf=10 s。

3.2 相关参数与控制器增益设定

起重机的各主要参数如表1所示。另外，应用试凑法设定控制器增益如表2所示。

表1 起重机参数

表2 控制器增益

3.3 干扰抑制

在本系统中，式(1)所指的外部干扰d除了包括非线性力还包括了如下所示摩擦项：

(17)

式中:C,fn分别表示粘性摩擦系数，静摩擦或库伦摩擦。fn的属性如图3所示，并可表示为下式：

(18)

式中:fs,fc分别表示静摩擦和库伦摩擦，其数值由实验得C=1.39N·m/(rad/s),fs=3.71N·m,fc=3.58N·m。

图3 摩擦模型

首先，干扰观测器对于摩擦干扰影响的抑制效果如图4所示。干扰观测器的截止角频率是调节系统稳定性和干扰抑制性能之间权衡的重要参数。本研究应用试凑法确定。所有角速度是通过后向差分法计算获得。尽管在图4(a)中无论实验还是仿真都和目标轨道相一致，但是在图4(b)中却存在着很大的跟踪误差。因此，可知通过使用干扰观测器旋转角的定常误差得到很好的改善。

其次，干扰观察器对于荷载质量变化影响的抑制效果如图5所示。在该仿真中，忽视了关节间摩擦的影响。在图5(a)中，旋转角θ4的跟踪特性没有因为荷载质量大幅地变化而变化，从而证实了干扰观测器对荷载质量变化具有鲁棒性。

旋转起重机的动力学模型可由式(1)～(3)描述。在式(2)和(3)中并不包含荷载质量参数，是因为影响悬绳-荷载振动系统固有频率的主要因素是悬绳长度。因此，在讨论对于荷载质量变化的鲁棒性问题时只需考虑式(1)即可，可将其质量变化的影响归结到式(1)中的干扰项d，并使用干扰观测器进行补偿。

3.4 比较仿真

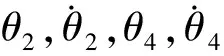
y=cTx

(19)

式中:α=g/l,γ=Lsinθ3/l。

图4 干扰观测器对摩擦抑制效果

图6 含有积分器的线性状态反馈控制系统

在本小节中，所设计的含有积分器的LSFC如图6所示。图中P,k,KI,v,r,y分别表示起重机线性模型，四阶状态反馈矢量，积分器增益，控制输入，旋臂目标信号和控制输出。

表3 线性状态反馈控制器增益

在本小节中，所设计的含有积分器的LSFC如图6所示。图中P,k,K1,v,r,y分别表示起重机线性模型，四阶状态反馈矢量，积分器增益，控制输入，旋臂目标信号和控制输出。

通过求解一个具有以下目标函数的最优化问题得出控制器增益，其数值如表3所示。

(20)

式中:Q=diag{1 500,315,1 500,315,50},R=1

仿真结果如图7所示。图中分别表示旋转角θ4，指令电压u，起伏方向摆角θ1以及旋转方向摆角θ2。虽然在图7(a)中旋转角几乎与目标轨道一致且在图7(d)中旋转方向的摆角θ2得到很好的抑制，但是在图7(c)中起伏方向的摆角θ1却无法得到抑制。

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

在不改变LSFC增益的前提下只改变目标旋转角度θ4f=25°和θ4f=65°，其仿真结果如图8和9所示，并得到了与图7几乎相同的结果。因此，线性控制器不能用来解决本文中所提出的控制问题。

3.5 实验设备

图10 实验系统

如图10所示的系统由驱动旋臂旋转运动的直流电动机，旋臂，悬绳，荷载以及测量摆角的电位计等部分构成。旋转角可由光电编码器测得，其角度测量分辨率为1.8×10-3°。

测量摆角的传感器系统如图11所示。测量起伏方向摆角θ1的电位计1固定在旋臂上。测量旋转方向摆角θ2的电位计2固定在部件1上，并围绕电位计1的旋转轴旋转。部件2和长杆共同围绕电位计2的旋转轴旋转。部件3相对于长杆，部件4相对于部件3分别旋转。部件4可沿着吊绳滑动。其角度测量分辨率为6.4×10-2°。

图11 测量摆角的传感器系统

3.6 实验验证

本小节通过仿真和实验来验证新方法的有效性。其结果如图12所示。图中分别表示旋转角θ4，指令电压u，起伏方向摆角θ1以及旋转方向摆角θ2。图12(a)中无论是仿真结果还是实验结果旋转角几乎与目标轨道一致，并得到与图7(d)几乎相同的结果，但是对于起伏方向的摆角θ1的抑制，新方法则得到了较好的抑制效果。

在不改变控制器增益的前提下只改变旋转角的目标值θ4f=25°和θ4f=65°，其结果如图13和14所示，并得到了与图12几乎相同的结果。

为了进一步验证新方法的有效性，在不改变控制器增益的前提下只改变起伏角θ3=30°和θ3=60°，其结果如图15和16所示，并得到了与图12几乎相同的结果。

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

(a)旋转角θ4 (b)指令电压U (c)起伏方向摆角θ1 (d)旋转方向摆角θ2

4 结 论

本文的目的在于只使用旋臂旋转运动同时实现起重机旋臂的高精度定位和荷载摆动抑制控制。为此，首先基于干扰观测器导出了起重机的部分线性模型。干扰观测器的使用使得该模型对于关节摩擦，荷载质量等参数变化具有鲁棒性。然后，提出了一种非线性控制器并基于李雅普诺夫稳定性定理分析了该系统的稳定性。该控制器解决了起重机在目标位置附近的线性化系统的不可控问题。最后，通过比较仿真以及实验验证了该方法的有效性。无论是改变旋转角的目标值还是改变起伏角，都实现了旋臂的跟踪特性和摆角的抑制特性。该方法为简化起重机结构和增加其安全性提供了一种可能。

然而，由于悬绳长度的变化会影响系统的稳定性以及控制性能，接下来将该方法扩展到绳长变化的情况。

参 考 文 献

[1]Ahmad M A,Ramli M S,Ismail R M T R.Infinite impulse response filter techniques for sway control of a lab-scaled rotary crane system[C].Second International Conference on Computer Modeling and Simulation,22-24 Jan.,Sanya,2010,192-196.

[2]Terashima K,Shen Y,Yano K.Modeling and optimal control of a rotary crane using the straight transformation method[J].Control Engineering Practice,2007,15: 1179-1192.

[3]沈 滢,曹金城,王 玲.旋转起重机建模及负载摆动最优控制[J].沈阳建筑大学学报(自然科学版),2009,3(25): 605-608.

SHEN Ying,CAO Jin-cheng,WANG Ling.Modeling of a rotary crane and the optimal control for load swing[J].Journal of Shenyang Jianzhu University (Natural Science),2009,3(25): 605-608.

[4]Liu D,Yi J,Zhao D,et al.Adaptive sliding mode fuzzy control for a two-dimensional overhead crane[J].Mechatronics,2005,15: 505-522.

[5]Lee H H,Liang Y,Segura D.A sliding-mode anti swing trajectory control for overhead cranes with high-speed load hoisting[J].Transactions of the ASME,Journal of Dynamic Systems,Measurement,and Control,2006,128: 842-845.

[6]Yang J H,Yang S K.Adaptive coupling control for overhead crane systems [J].Mechatronics,2007,17: 143-152.

[7]Tsai C C,Wu H L,Chuang K H.Back stepping aggregated sliding-mode motion control for automatic 3D overhead cranes[C].IEEE/ASME International Conference on Advanced Intelligent Mechatronics,11-14 July,2012,Kaohsiung,849-854.

[8]Yazied T G,Hagag S Y,Ajmi M S,et al.Nonlinear modelling and vibration control of jib cranes[J].World Applied Sciences Journal,2012,16(11),1543-1550.

[9]Ohto M,Yasunobu S.A rotary crane control method based on a skillful operator’s knowledge[J].Transactions of the Society of Instruments and Control Engineers (In Japanese),1997,33(9): 923-929.

[10]Kondo R,Takeda T,Tagchi H,et al.Sway control for rotary crane based on load swing period[J].Transactions of the Japan Society of Mechanical Engineers(C)(In Japanese),2000,67(655): 725-731.

[11]Nakazono K,Ohnishi K,Kinjo H,et al.Vibration control of load for rotary crane system using neural network with GA-based training[J].Artificial Life and Robotics,2008,13: 98-101.

[12]Kondo R,Shimahara S.Anti-sway control of a rotary crane via two-mode switching control[J].Transactions of the Society of Instruments and Control Engineers (In Japanese),2005,41(4): 307-31.