2024-T3铝合金动力学实验及其平板鸟撞动态响应分析

刘 富,张嘉振 ,童明波 ,胡忠民 ,郭亚洲 ,臧曙光

(1.中国商飞北京民用飞机技术研究中心，北京 102211；2.南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016；3.西北工业大学 航空学院，西安 710012；4.中国建筑材料检验认证中心，北京 100024)

鸟撞是发生在毫秒量级内的瞬态冲击现象。撞击过程中，鸟体与被撞结构之间存在着强烈的耦合效应，因此鸟撞问题是一个非常复杂的非线性瞬态动力学及流固耦合问题[1]。在典型的鸟撞速度下，鸟体呈现出明显的流体飞溅状态，鸟体的冲击行为从而可近似认为是水动力行为。SPH方法作为一种基于拉格朗日技术的自适应无网格粒子法，将其和有限元方法进行耦合，在流固耦合问题求解中具有显著的优势[2-3]。McCarthy等[4]采用SPH单元模拟鸟体，对纤维金属层板结构机翼前缘及夹具采用拉格朗日单元模拟，通过定义鸟体和结构的耦合作用进行鸟撞数值分析，计算与试验的一致性证明了SPH方法在求解这类结构鸟撞问题方面的可行性和准确性。Georgiadis等[5]利用PAM-CRASH软件，通过耦合SPH方法和有限元方法进行了B787飞机碳纤维复合材料机翼前缘缝翼的鸟撞仿真计算，提高了设计效率，降低了适航取证成本。刘军等[6]基于SPH方法进行了平板叶片的鸟撞数值模拟，通过与拉格朗日方法及试验结果进行对比，指出SPH方法比拉格朗日方法更接近试验结果。

铝合金作为最常用的一种航空材料，其力学性能不仅与材料本身的内部结构有关，还与外部条件如加载速率、环境温度等相关。材料的本构模型是影响鸟撞计算精度的关键因素之一，在鸟体高速撞击过程中，一般均要考虑到材料的应变率强化效应，因此通过动态力学试验测得材料的动态力学性能尤为重要。张伟等[7]使用万能材料试验机、扭转试验机和Taloy撞击试验研究了高强铝合金7A04不同温度下的准静态、动态本构关系和失效模型。林木森等[8]运用材料试验机和霍普金森压杆装置对3种不同加工及热处理状态的5A06铝合金在不同温度、应变率为10-4～103s-1下的力学行为进行了实验研究，并基于Johnson-Cook模型，确定了三种状态下的动态本构关系。McCarthy等[9]通过普通拉伸试验机和霍普金森拉杆分别对纤维金属层板材料进行准静态、中等应变率和高应变率下的拉伸试验，获得不同应变率下的力学特性，为纤维金属层板机翼前缘结构的鸟撞分析提供必要的材料本构和失效参数。Hanssen等[10]基于ALE方法，通过数值计算获得了泡沫铝夹心结构的鸟撞动态响应，其中夹心结构两侧的铝合金薄板本构模型通过材料动态拉伸试验获得。

本文中，使用电子万能试验机进行2024-T3铝合金的准静态力学性能研究；利用SHTB获得2024-T3铝合金在高应变率下的应力-应变关系，通过对拉伸试验获得的应力-应变曲线拟合得到描述2024-T3铝合金动态本构关系的Johnson-Cook模型方程。基于PAM-CRASH软件，结合2024-T3铝合金动态力学性能试验所获得的Johnson-Cook方程，耦合SPH方法和有限元方法建立2024-T3铝合金平板的鸟撞数值模型，并通过相对应的鸟撞试验对数值计算模型进行验证。

1 动态力学性能试验及本构关系拟合

1.1 动态力学性能试验

为了确定2024-T3铝合金材料在不同应变率下的动态力学性能，通过电子万能拉伸试验机进行2024-T3铝合金的准静态拉伸试验，采用SHTB拉伸试验获得2024-T3铝合金高应变率下的力学特性，文中对于外界温度变化对材料力学特性的影响不做研究，所有试验均在室温下进行。

试验件通过楔形夹具夹持在电子万能试验机上，利用引伸计测量试验件的应变，共进行0.001/s和0.01/s两种应变率下的拉伸试验，每种应变率下至少进行三组试验，如图1所示。

图1 准静态拉伸试验

SHTB是测量材料动态力学性能的常用试验设备，应变率测量范围可以从102/s至104/s，其试验技术核心为一维应力波理论，图2给出了SHTB的加载示意图。工程应力、工程应变及应变率分别由以式(1)求得：

(1)

(2)

(3)

式中:E是加载杆的弹性模量，A和As分别为加载杆和试验件的截面积，L为试验件的长度，C0为波速。εI(t)，εR(t)和εT(t)分别代表了入射应变、反射应变和透射应变。

图2 SHTB加载示意图

根据试件外形和尺寸，设计专用接头，将试件安装于SHTB上，如图3所示，共进行900/s、1 100/s和1 300/s三种应变率下的拉伸试验。

图3 SHTB拉伸试验

图4显示了SHTB试验中，示波器记录的典型波形。图5给出了2024-T3铝合金在准静态和高应变率下的应力-应变曲线。从图中可以看出2024-T3铝合金所表现出的应变率强化效应：高应变率下的材料屈服强度较准静态下有了明显的增大，经计算从应变率0.001/s 下的289.05 MPa上升至900/s 的370.2 MPa，这表明2024-T3铝合金对应变率还是比较敏感的。在同一应变率区间范围内，如准静态或高应变率下，材料的动态力学性能则基本相近。

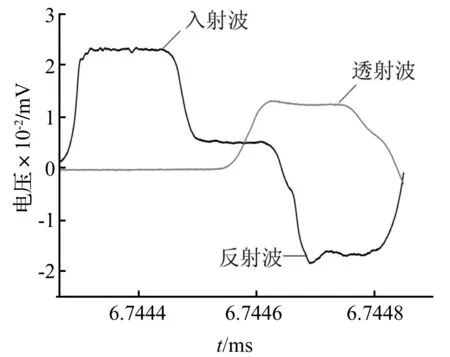
图4 示波器记录的SHTB动态拉伸试验典型波形

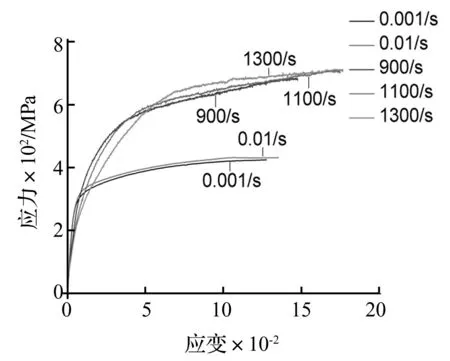
图5 5种应变率下的应力-应变曲线

1.2 Johnson-Cook本构模型拟合

Johnson-Cook模型是一个能反映金属等材料应变硬化效应、应变率强化效应及温度软化效应的材料模型[11,12]，表达式如下：

(4)

本文不考虑材料的温度软化效应，对应力-应变曲线进行拟合只需得到Johnson-Cook模型方程中的A、B、C和n这4个参数，拟合步骤如下。

(1)确定A、B和n

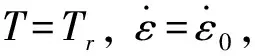
σ=A+Bεn

(5)

取0.001/s为参考应变率，根据该准静态试验下的应力-应变曲线求得参数A、B和n。

(2)确定C

C为材料应变率敏感系数。当塑性应变ε=0、T=Tr，室温下的动态屈服应力和应变率的关系为:

(6)

根据除0.001/s外的另外四组应变率下的应力-应变曲线，则可以得到常数C。

最终拟合所得到的4个参数值如表1所示。Johnson-Cook本构模型拟合结果与试验结果对比如图6所示，拟合点与曲线较好的重合性表明了拟合所得的Johnson-Cook模型表达式能够比较准确的反映2024-T3铝合金材料的本构关系。

表1 2024-T3铝合金Johnson-Cook本构模型参数

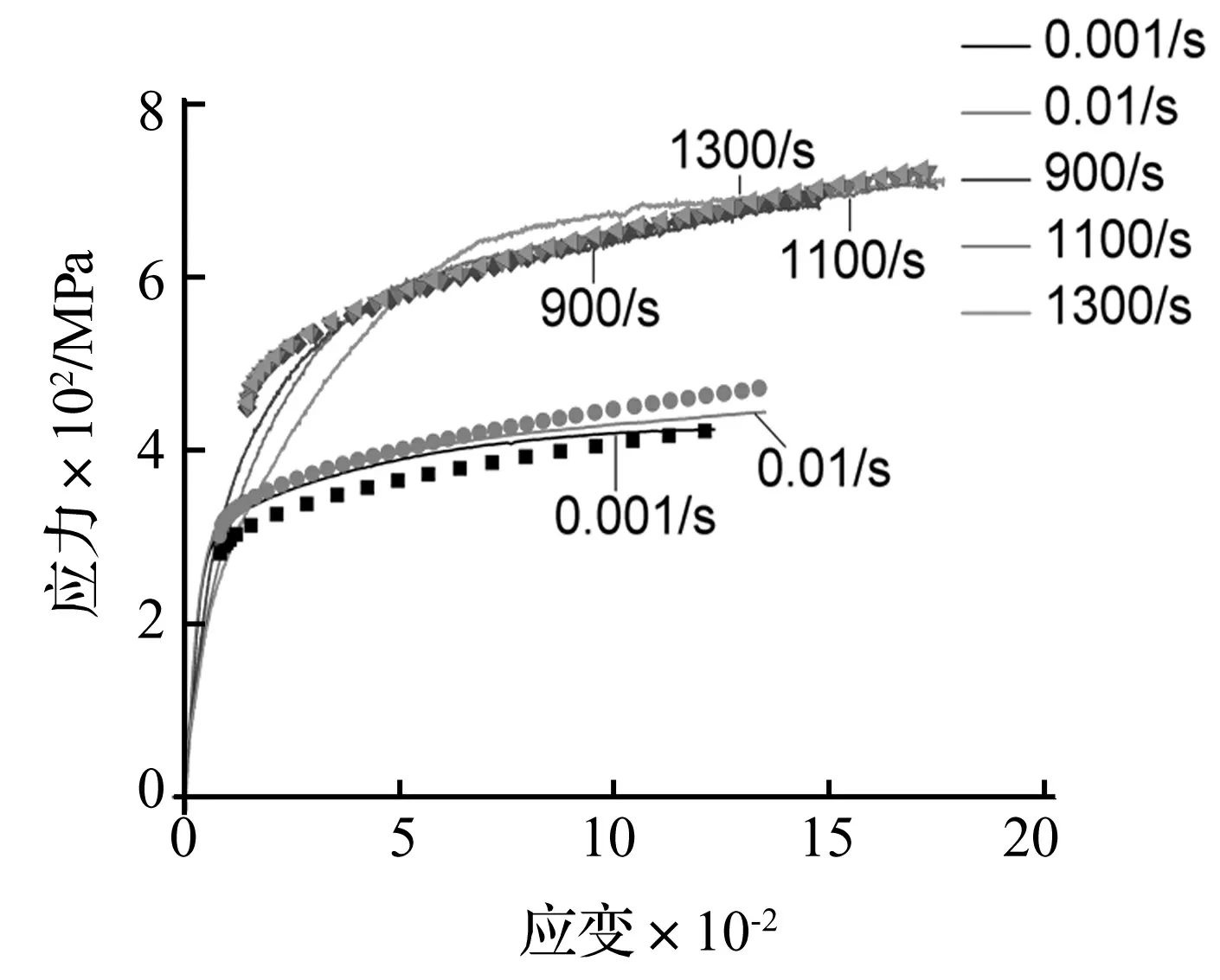
图6 Johnson-Cook模型拟合结果与试验对比

2 铝合金平板鸟撞数值计算及试验验证

2.1 数值计算

鸟体形状为中间圆柱、两端半球的柱体，长度和直径的比值为2。鸟体质量取1.8 kg，密度为950 kg/m3。为了避免大变形出现网格畸变的问题，同时更好的模拟鸟撞过程中的鸟体破碎、飞溅，采用SPH单元来模拟鸟体。引入Mornaghan EOS状态方程[13-15](式(7))定义鸟体的本构模型。

(7)

式中:P0表示初始压力，ρ0为鸟体初始密度。B和γ为常数，通过数值计算结合鸟撞试验优化反演得到，本文取B=128×106，γ=7.98[4]。

图7为建立的2024-T3铝合金平板鸟撞数值计算模型，试验件夹具采用实体单元模拟，2024-T3铝合金平板采用Beltyschko-Tsay壳元模拟，连接平板和夹具的螺栓采用实体单元模拟。2024-T3铝合金本构模型则采用动态力学性能试验获得的Johnson-Cook模型。通过定义鸟体和平板之间的耦合接触来实现SPH方法和有限元方法的耦合；平板与夹具之间定义普通接触。试验中，夹具四角通过四颗螺栓固定在台架上，在数值计算模型中对这四个部位进行固支约束来模拟真实情况。平板的长和宽均为600 mm，厚度为4.8 mm，撞击点为平板的中心，分别通过应变片和位移传感器测量测试点的应变和位移，平板试验件安装如图8所示。由于应变片在高速冲击载荷作用下很可能会被拉断或脱胶而造成数据丢失，为了尽可能的获得完整的数据，在和测试点(S1、S2、S3和S4)关于平板对角线对称的位置上布置了另外四组应变片(S5、S6、S7和S8)，八组应变片及位移传感器(测试点D1和D2)布置如图9所示。

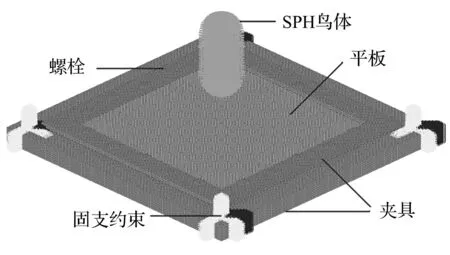
图7 鸟撞数值计算模型

图8 平板试验件安装

图9 应变、位移测量装置及示意图

2.2 结果讨论

图10给出了鸟体以100 m/s的速度撞击2024-T3铝合金平板的撞击过程数值模拟与高速摄像的对比。当鸟体高速撞上平板，鸟体和平板之间会产生很强的冲击压力，此时鸟体内部会形成与撞击速度方向相反的冲击波，鸟体被压缩逐渐膨胀，冲击压力下降；随着时间的推进，鸟体贴着平板沿径向扩散，最终呈液体状飞溅。从数值模拟和高速摄像的对比可以看出，数值计算模型比较真实的模拟了鸟撞的整个过程；另外，等效塑性应变云图清楚的显示了应力集中区域主要为平板撞击中心位置及螺栓连接处。

图10 数值模拟与高速摄像对比

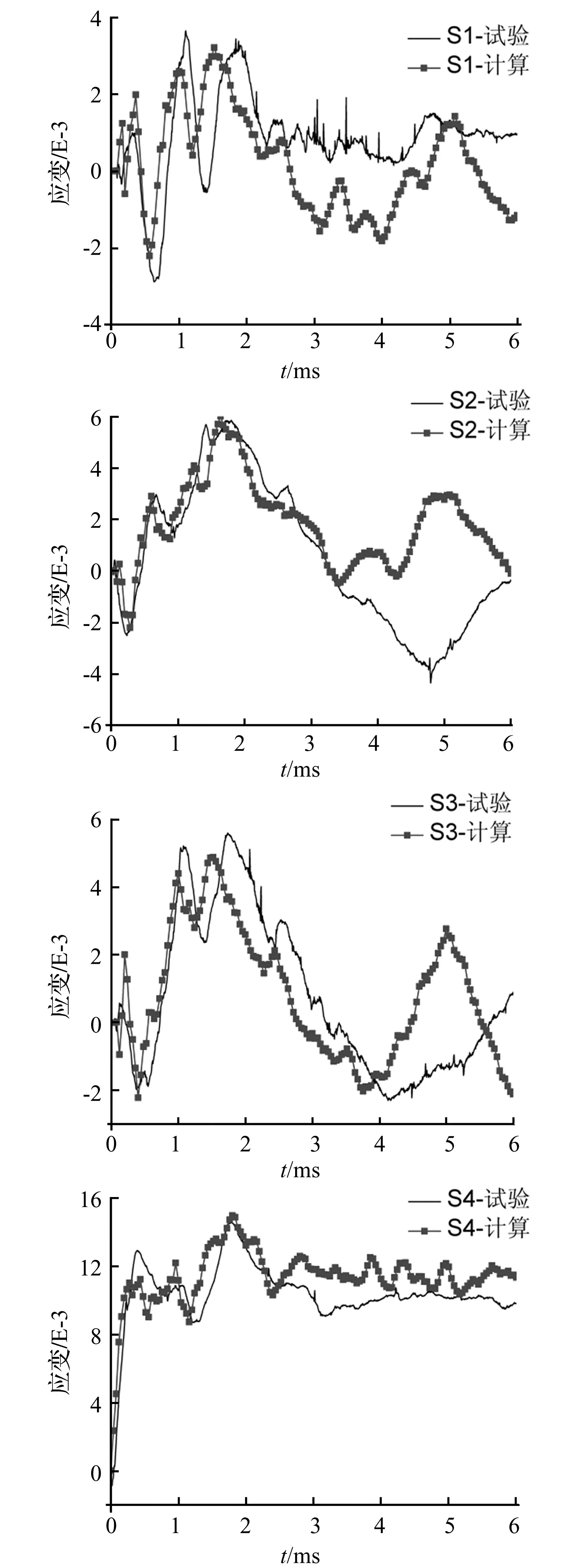
图11 计算和试验对比—应变-时间曲线

测试点应变-时间曲线、位移-时间曲线的计算和试验对比分别如图11和图12所示。从图中可以看出，计算所得位移、应变的变化趋势、大小以及最大载荷峰值、出现的时间和试验基本吻合。整个撞击过程大约在6 ms内完成，结合图10高速摄像及数值模拟的撞击过程对图11、12进行分析：撞击初始阶段，鸟体对平板的冲击载荷伴随着鸟体局部的压缩逐渐增大，图11和图12显示应变和位移的最大峰值出现在2 ms左右，即在这个时刻平板受到的载荷最大；鸟体在压缩作用下膨胀并沿径向扩展，鸟体内部压力降低，平板应变和位移逐步减小，并伴有小幅度的震荡，直至鸟体全部消耗，撞击过程结束，在测试点S4即撞击中心处留下了应变大约为0.012的塑性变形。由图11和图12均可以看出，数值计算所得的应变、位移时间相位比试验有所提前，这和采用SPH方法模拟鸟体所定义的人工粘性系数取值有关。另外，数值计算得到的位移峰值小于试验值，通过对鸟撞录像进行分析，可以发现在鸟体高速撞击作用下，连接夹具和试验台架的螺栓并没有完全卡紧夹具，导致夹具整体沿着撞击速度方向出现了小幅的刚体位移，因此位移传感器记录的平板测试点位移实际为夹具的刚体位移与测试点变形之和，测量结果偏大。

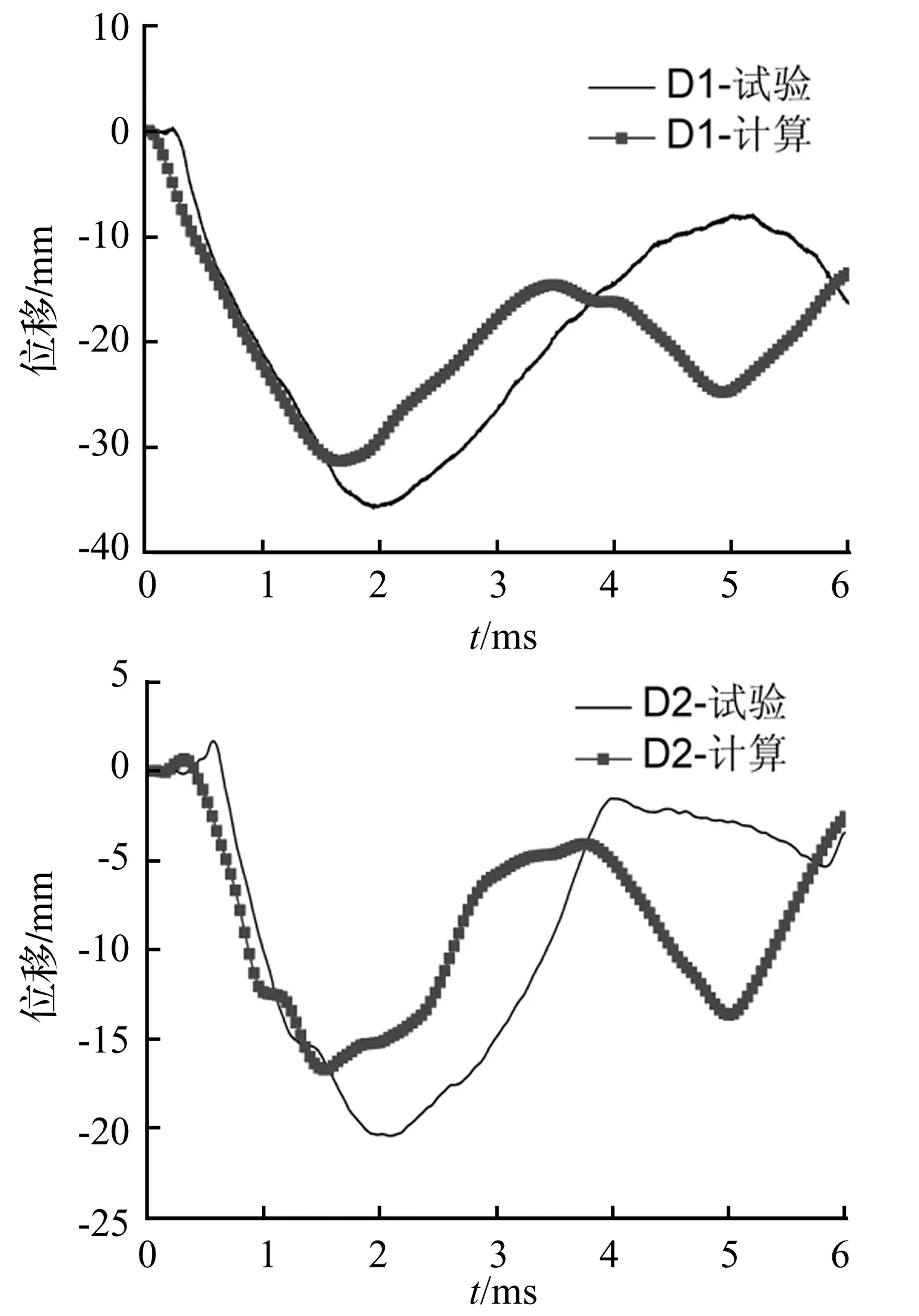
图12 计算和试验对比—位移-时间曲线

3 结 论

采用电子万能试验机、SHTB分别进行2024-T3铝合金准静态和高应变率下的拉伸试验，获得了材料在不同应变率下的动态力学特性；拟合得到能够反映2024-T3铝合金材料硬化效应和应变率强化效应的Johnson-Cook模型方程。

基于PAM-CRASH软件建立了2024-T3铝合金平板的鸟撞数值模型，引入Mornaghan EOS状态方程定义鸟体的本构模型，2024-T3铝合金材料本构模型采用动态力学性能试验获得的Johnson-Cook模型，通过耦合SPH方法和有限元方法计算获得了2024-T3铝合金平板在高速撞击下的动态响应。针对数值计算开展相对应的平板鸟撞试验验证，计算结果和试验结果较好的一致性和吻合性表明建立的数值计算模型是合理、可靠的。

本文中材料动态拉伸试验受试验机性能的限制，无法获得材料在中等应变率下的动态力学特性，在下一步的研究中拟采用高速拉伸试验机进行材料的动态拉伸试验，得到材料在中等应变率下的应力-应变曲线，以进一步完善Johnson-Cook本构模型的参数拟合工作。

参 考 文 献

[1]Heimbs S.Computational methods for bird strike simulations: A review [J].Computers and Structures,2011,89 (23-24): 2093-2112.

[2]Guida M,Marulo F,Meo M,et al.SPH-Lagrangian study of bird impact on leading edge wing [J].Composite Structures,2011,93 (3): 1060-1071.

[3]Vuyst T D,Vignjevic R,Campell J C.Coupling between meshless and finite element methods [J].International Journal of Impact Engineering,2005,31(8): 1054-1064.

[4]McCarthy M A,Xiao J R,McCarthy C T,et al.Modeling of bird strike on an aircraft wing leading edge made from fibre met al laminates Part2: modeling of strike with SPH bird model [J].Applied Composite Materials,2004,11(5): 317-340.

[5]Georgiadis S,Gunnion A J,Thomson R S,et al.Bird-strike simulation for certification of the Boeing 787 composite moveable trailing edge [J].Composite Structures,2008,86(1-3): 258-268.

[6]刘 军,李玉龙,刘元镛.基于SPH方法的叶片鸟撞数值模拟研究 [J].振动与冲击,2008,27(9): 90-93.

LIU Jun,LI Yu-long,LIU Yuan-yong.Numerical simulation study of bird-impact on a blade using SPH method [J].Journal of vibration and shock,2008,27(9): 90-93.

[7]张 伟,肖新科,魏 刚.7A04铝合金的本构关系和失效模型[J].爆炸与冲击,2011,31(1): 81-87.

ZHANG Wei,XIAO Xin-ke,WEI Gang.Constitutive relation and fracture model of 7A04 aluminum alloy [J].Explosion and shock waves,2011,31(1): 81-87.

[8]林木森,庞宝君,张 伟,等.5A06铝合金的动态本构关系实验 [J].爆炸与冲击,2009,29(3): 306-311.

LIN Mu-sen,PANG Bao-jun,ZHANG wei,et al.Experimental investigation on a dynamic constitutive relationship of 5A06 Al alloy [J].Explosion and shock waves,2009,29(3): 306-311.

[9]McCarthy M A,Xiao J R,Petrinic N,et al.Modeling of bird strike on an aircraft wing leading edge made from fibre met al laminates Part1: material modeling [J].Applied Composite Materials,2004,11(5): 295-315.

[10]Hanssen A G,Girard Y,Olovsson L,et al.A numerical model for bird strike of aluminium foam-based sandwich panels [J].International Journal of Impact Engineering,2006,32(7): 1127-1144.

[11]Johnson G R,Cook W H.Fracture characteristics of three metals subjected to various strains,strains rates,temperatures and pressures [J].Engineering Fracture Mechanics,1985,21(1): 31-48.

[12]Pothnis J R,Perla Y,Arya H,et al.High strain rate tensile behavior of aluminum alloy 7075 T651 and IS 2062 mild steel [J].Journal of Engineering Materials and Technology,2011,133(2): 1-9.

[13]Monaghan J J.Simulating free surface flow with SPH [J].Journal of Computational Physics,1994,110(2): 399-406.

[14]Monaghan J J,Kocharyan A.SPH simulation of multiphase flow [J].Computer Physics Communication,1995,87(1-2): 225-235.

[15]Sheikh M Z,Li Y L.Dynamic response of the leading edge wing under soft body impact [J].International Journal of Crashworthiness,2012,17(4): 357-376.