基于核递推最小二乘的自适应均衡的弱故障提取方法研究
李志农,赵 匡,邬冠华
(1.南昌航空大学 无损检测技术教育部重点实验室,南昌 330063;2.郑州大学 机械工程学院,郑州 450001)
安装在机器上的传感器所测得的信号不可避免地要受到传递路径以及其它部件正常振动和噪声的影响。尤其是早期的故障,一般冲击比较轻微,隐藏在系统的总体振动中,很难被发现。而后期严重的冲击可能导致二次损伤和重大事故。然而,现有的基于信号处理的故障诊断方法如文献[1-3]仅对输出信号进行分析,并不能抑制传递通道的影响。为解决此不足,在此,将通信工程中的均衡思想引入到机械故障诊断中,为解决通道的影响提供了一种新的思路。
传统的自适应均衡算法主要集中在最小均方(LMS)类和递归最小平方(RLS)类。LMS类算法一般采用近似的最速下降法,然而,这种近似带来了两个缺点,一是引入了抽头系数的噪声项,导致稳态失调量较大,二是收敛速度变慢,对非平稳信号的适应性差,算法的信号跟踪补偿能力下降。RLS算法虽然克服了LMS算法的一些不足,但是,RLS算法的计算复杂度高,所需的存储量大,不利于实时实现,若被估计的自相关矩阵的逆矩阵失去了正定特性,将导致算法的发散。
针对传统的自适应均衡算法存在的不足,本文将核递推最小二乘法(Kernel Recursive Least-Square,KRLS)[4-5]引入到自适应均衡中,提出了一种基于KRLS的自适应均衡算法,并与传统的自适应均衡算法进行对比分析。在此基础上,将基于KRLS自适应均衡思想引入到机械故障诊断中,提出了一种基于KRLS自适应均衡的机械故障诊断方法,该方法能有效地消除传递通道影响。仿真和实验验证了提出的方法的有效性。
1 基于KRLS的自适应均衡算法
给定系统的输入输出模型为:
Y(n)=H(n)R(n)+E(n)
(1)
其中,R(n)是系统的输入,H(n)是系统的输出,E(n)是系统的噪声,H(n)是系数矩阵。传统的递推最小二乘算法是致力于误差δn平方和最小化,即:
(2)
其中,dn是一个向量,包含当前所有数据的期望输出dn=[d1,…,dn]T。w是更新向量权值。每次迭代中通过新到来的数据点和期望输出来更新权值向量w,直到满足迭代终止条件,最终输出的w即为所求的权值向量,或称之为滤波器系数。而核递推最小二乘均衡算法则是在特征空间中实施标准最小二乘算法。在迭代次数为n时,KRLS致力于式(3)最小化:
(3)
其中Kn是当前所有可见数据{x1,…,xn}的核矩阵,αn是所要求的权值向量。通过选取适当的核函数,即可计算出样本数据的核矩阵,它的维数等于所选取的数据点数,且为对角方阵[7]。因为假设的最小二乘误差是越接近于0越好的,因此,由式(3),可取权值向量αn的估计为:
(4)
(1)初始化:
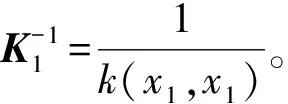
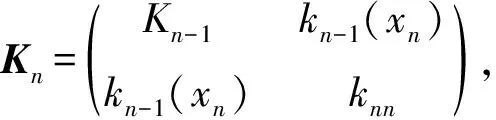
(3)当迭代次数达到采样总数据点数之后,算法结束,输出权值向量αn。
2 仿真研究
为了验证提出的方法的有效性,这里以非线性特性明显的麦克格拉斯延迟微分方程为例进行仿真,其表达式如下:
(5)
其中,a=0.1,b=0.2,时间常数τ=30,采样数据长度为500,给定的输入为一周期脉冲信号,并加入信噪比为40 dB的高斯噪声干扰,脉冲时间间隔为0.08 s,采样频率fs=1 000 Hz。由四阶龙格库塔算法可求得其输出,输出信号波形如图1所示,利用得到的输入和输出信号,采用本文提出的方法对其做均衡,均衡结果如图2所示。
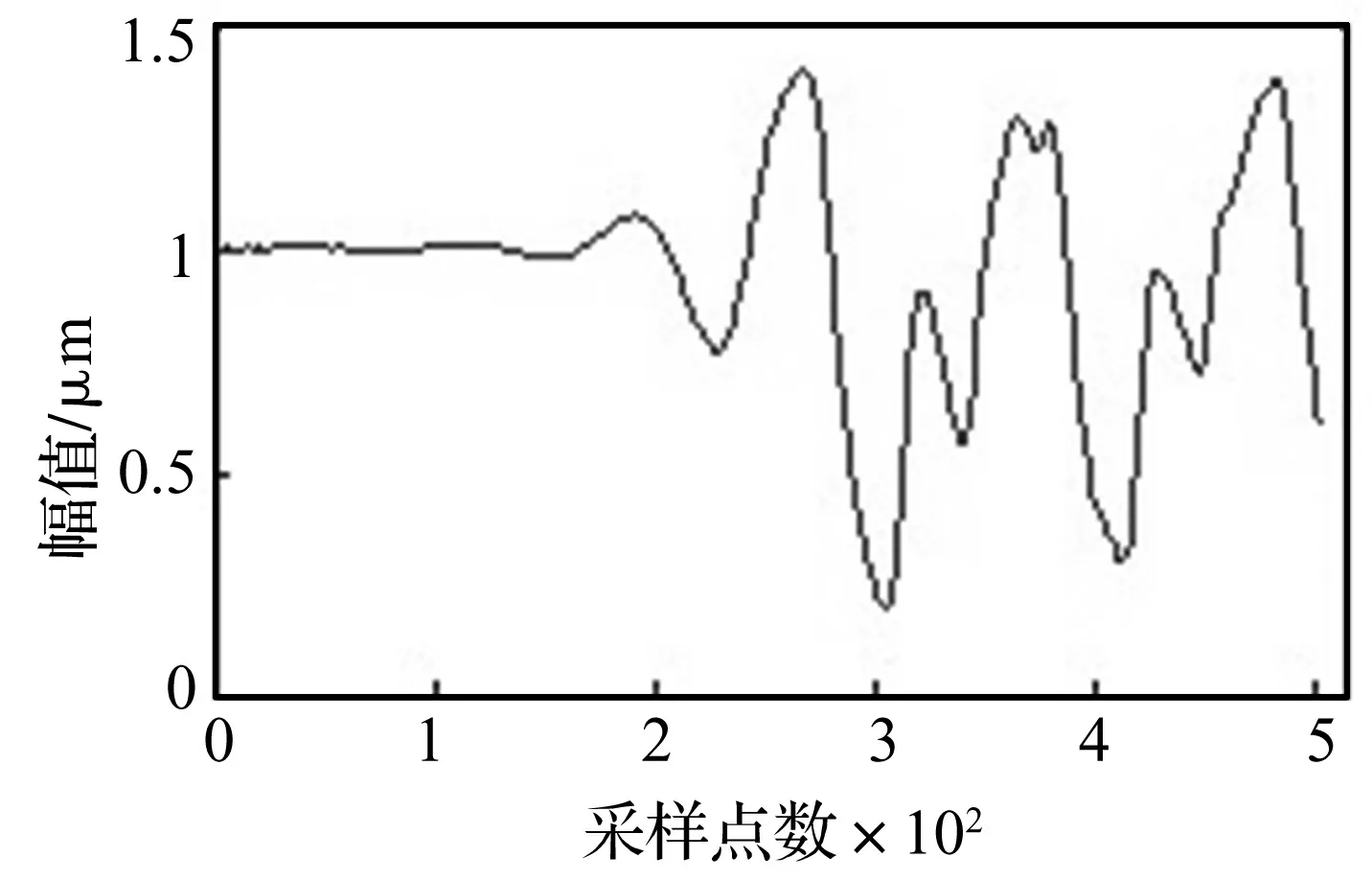
图1 输出信号波形
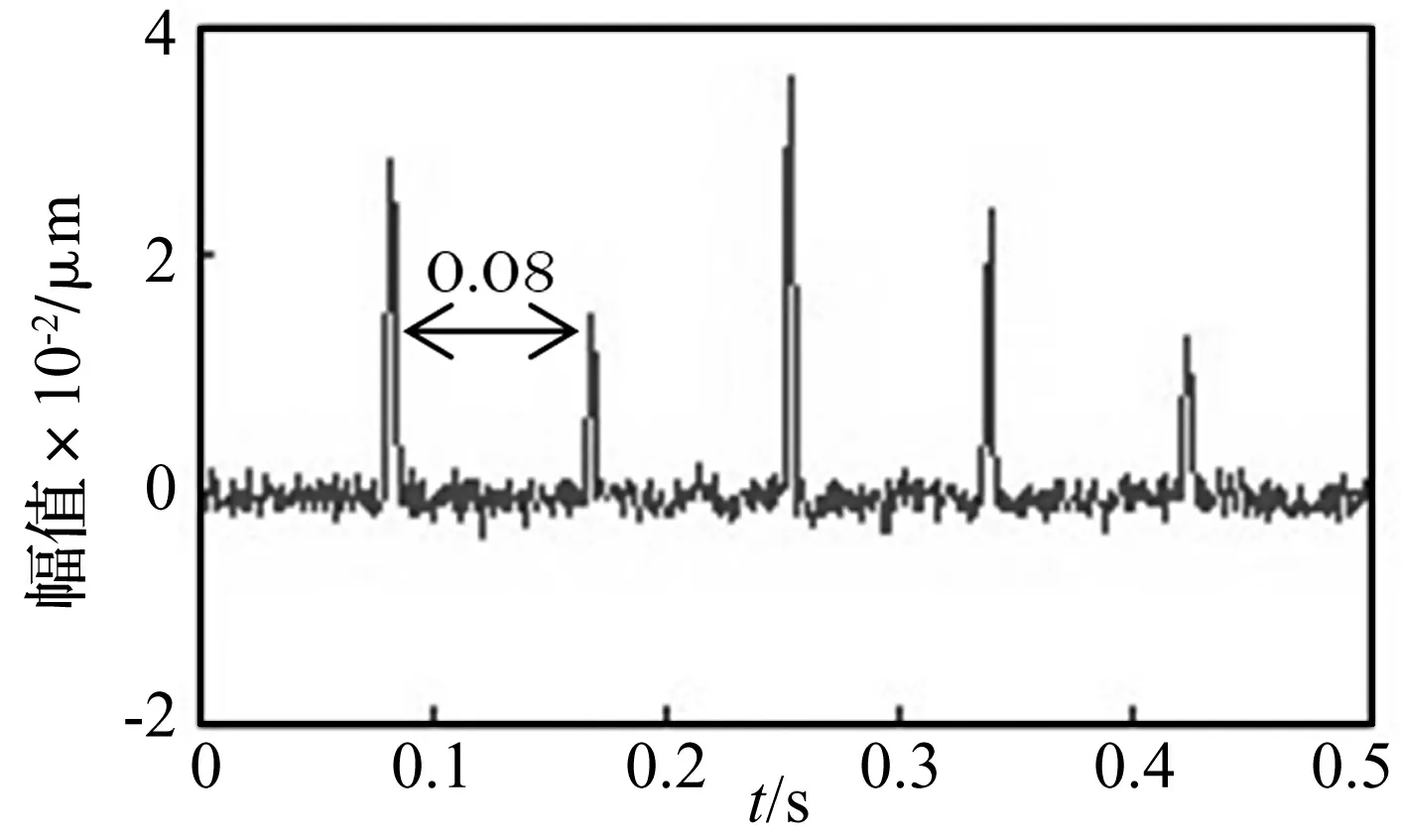
图2 KRLS重建的冲击信号
由图1可知,很难看出信号中存在冲击成分,然而,从图2中可以看到周期性的冲击信号被很好的还原出来,冲击时间间隔为0.08 s,正好对应着其脉冲冲击时间间隔,而残留的高斯噪声误差很小。仿真结果表明,KRLS均衡算法具有从强干扰的信号中抽取冲击脉冲信号的能力,因此,该方法适合用于提取弱冲击性故障。
为了比较,在此,采用了基于LMS的自适应均衡方法和基于RLS的自适应均衡方法对上述模型进行均衡,均衡结果分别如图3和图4所示。
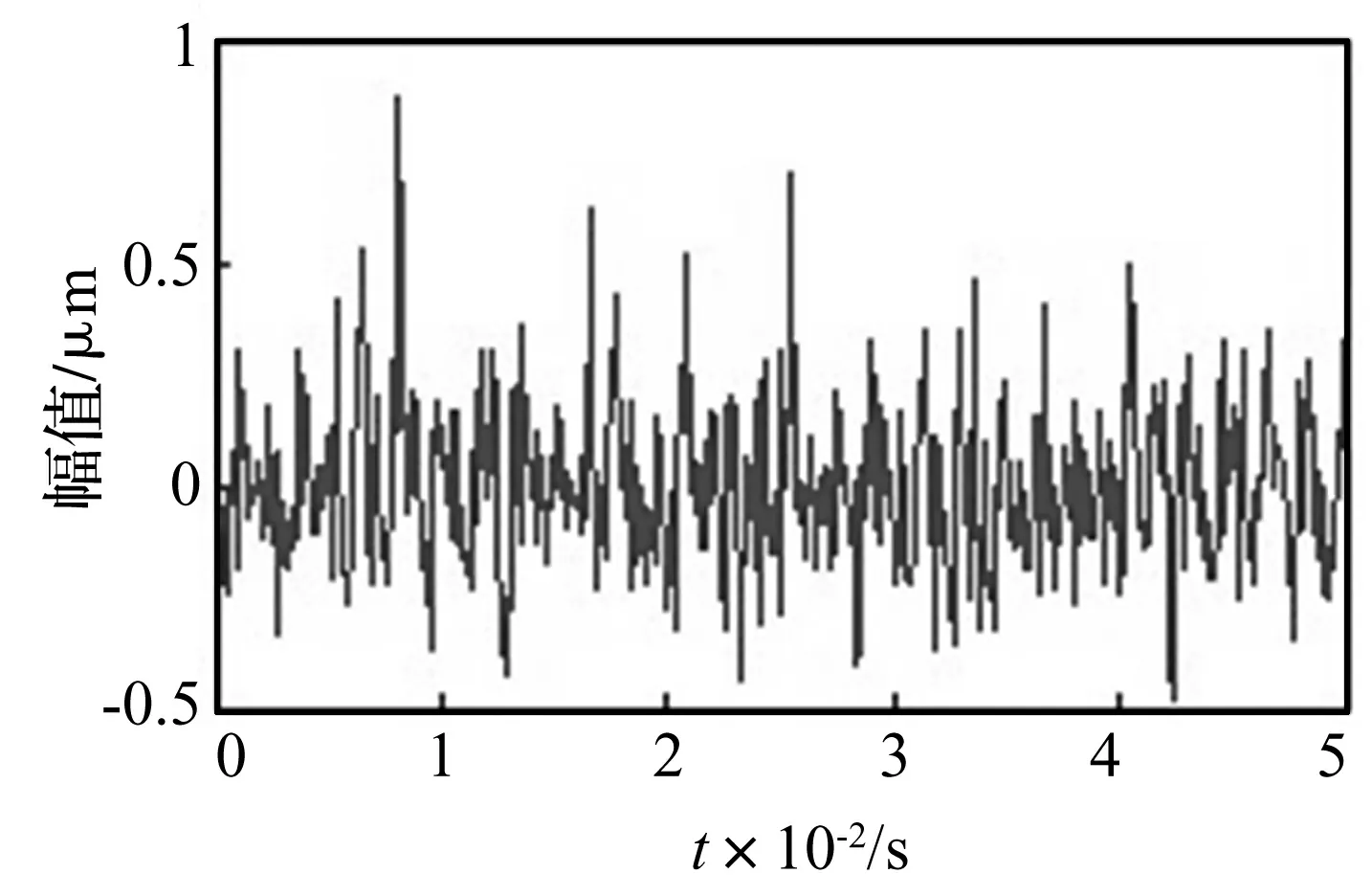
图3 LMS重建的冲击信号
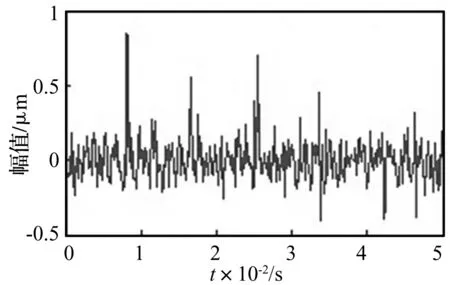
图4 RLS重建的冲击信号
对比图2、图3和图4,KRLS在算法适应性,跟踪能力和抗干扰能力方面均优于传统的LMS和RLS均衡算法。图3中,LMS均衡算法得到的冲击信号几乎完全淹没在高斯噪声中,在低信噪比和时变信号中, LMS均衡效果并不理想,对非平稳信号的适应能力很差,信号跟踪和抗干扰能力明显不足。由图4可看出,RLS均衡效果优于LMS均衡方法,恢复了部分冲击信号,但是仍然残存较高误差的高斯噪声,RLS均衡算法对噪声的抗干扰能力还有待提高。另外,RLS均衡算法还存在一个明显的缺陷,若被估计的自相关矩阵的逆矩阵失去了正定特性,将导致算法的发散。
3 实验研究
在与转子有关的各种故障中,裂纹故障占相当的比例,转轴出现裂纹的潜在危害性与一般故障的危害性相比较要严重得多,它是一种后果严重、诊断困难、又十分隐蔽的常发性故障,裂纹的存在已成为影响设备安全运行的一大隐患。如何有效地诊断转子裂纹的存在,尤其是早期裂纹的出现,一直是当今研究的热点之一。在此,将提出的方法应用到转子裂纹故障诊断中,验证提出的方法的有效性。
由于转子的偏心导致的简谐振动往往大于因裂纹故障导致的冲击振动,因此由裂纹产生的冲击振动信号往往淹没于转子不平衡产生的振动中。在此,通过KRLS均衡算法从转子振动信号中恢复弱小的冲击振动信号。
转子实验台示意图如图5所示[10],它是一个单跨单转子系统,包括电动机、联轴器、键相器、转轴、转盘、滑动轴承座(两个)和若干位移传感器,转子位于跨度中点。转子质量M=1 kg,转子不平衡量为M=6×10-5kg,材料属性(弹性模量E=2.1×1011Pa,密度ρ=7 800 kg/m3,泊松比ν=0.3),转子裂纹为一径向直裂纹,距转子边缘30 mm,深度为0.5 mm,裂纹转子的固有频率约为3 780 r/min,即特征频率为fn=36 Hz,转子转速为1 800 r/min。取传感器1测得的y向振动信号作为输入,传感器2测得的y向振动信号作为输出。对输入输出信号进行同步整周期采样,每周采集256点,数据采集8周,即总共数据2 048点。
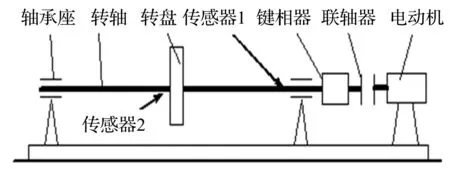
图5 转子试验台示意图
图6为传感器2测得的观测数据图,可以看出由转子测得的振动信号近似为正弦信号,看不出存在任何冲击。而实际上裂纹是存在的,由裂纹故障产生的微弱冲击完全淹没在转子的不平衡振动中。
图7为采用本文提出的方法均衡后得到的重建信号,相应的频谱图如图8所示。
图7中只显示了1 024个点,是因为在SW-KRLS均衡算法中采用的窗口大小为1 024,正好四个周期,所以重建的信号也只有四个周期。这样选择的目的是如果窗口选择太大,那么算法的计算时间复杂度和空间复杂度将会急剧增加,算法既耗时且精度的提升也不高。但是窗口也不能选择太小,起码要达到一个周期,才能保证信号处理不失真。为了方便对比和更好观测冲击信号,经实际验证,窗口选择为四个周期效果最好。
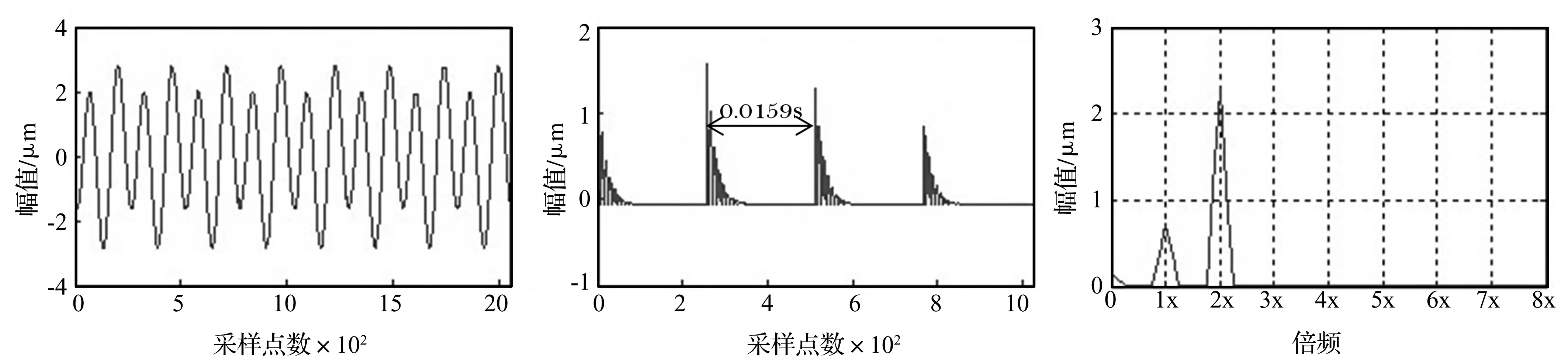
图6 观测信号波形
由图7可以看出,由于转子裂纹故障导致的弱冲击脉冲信号被很好的重建出来。冲击脉冲信号成指数形式衰减。由图8可以看出,当有裂纹存在时,系统输出不仅能反映出裂纹故障的1倍频成分,而且其2倍频也很明显,经计算冲击时间间隔为0.015 9 s,正好对应转子裂纹的特征频率。由此可知,本文提出的方法很好地提取了转子裂纹的故障信息。
4 结 论
本文将核递推最小二乘引入到非线性系统自适应均衡中,提出了一种基于KRLS的非线性系统自适应均衡方法,并进行了仿真。同时,将提出的方法分别与基于LMS的自适应均衡方法、基于RLS的自适应均衡方法进行了对比分析,仿真结果表明,KRLS均衡算法能有效地从强干扰的信号中抽取冲击脉冲信号的能力。与LMS、RLS均衡方法相比较,提出的方法在处理时变信号的适应性,信号跟踪和抗干扰能力方面明显优于这两种传统的方法。最后,将提出的方法应用到转子系统裂纹故障的提取中,实验结果进一步验证了提出的方法的有效性,该方法能很好地提取了转子裂纹的故障信息,本文的研究为机械故障诊断中消除通道传递特性的影响提供了一种新方法,具有重要的理论价值和实际应用价值。
参 考 文 献
[1]李志农,蒋 静,冯辅周,等.基于量子粒子群优化Volterra时域核辨识的隐Markov模型识别方法研究[J].仪器仪表学报,2011,32(12): 2693-2698.
LI Zhi-nong,JIANG Jing,FENG Fu-zhou,et al.Hidden Markov model recognition method based on Volterra kernel identified with particle swarm optimization[J].Chinese Journal of Scientific Instrument,2011,32(12): 2693-2698.
[2]李志农,刘卫兵,易小兵.基于局域均值分解的机械故障欠定盲源分离方法研究[J].机械工程学报,2011,47(7): 97-102.
LI Zhi-nong,LIU Wei-bing,YI Xiao-bing.Underdetermined blind source separation method of machine faults based on local mean decomposition[J].Journal of Mechanical Engineering,2011,47(7): 97-102.
[3]Li Z N,He Y Y,Chu F L,et al.Fault recognition method for speed-up and speed-down process of rotating machinery based on independent component analysis and factorial hidden markov model[J],Journal of Sound and Vibration,2006,291(1-2): 60-71.
[4]Van Vaerenbergh S.Kernel methods for nonlinear identification,equalization and separation of signals[D].University of Cantabria,2009.
[5]Shigeo A.Sparse least squares support vector training in the reduced empirical feature space[J].Pattern Analysis and Applications(PAA),2007,10(3): 203-214.
[6]Courant R,Hilbert D.Methods of mathematical Physics[M].American: Wiley-Interscience,1989.
[7]Ben-Hur A,Ong C S,Sonnenburg S,et al.Support vector machines and kernels for computational biology[J].PloS Computational Biology,2008,4(10): 1-10.
[8]Ilin A,Honkela A.Post-nonlinear Independent component analysis by variational bayesian learing[C].Proceedings of the Fifth International Conference on Independent Component Analysis and Blind Signal Separation (ICA 2004),Granada,Spain,September 2004,766-773.
[9]李志农,赵 匡,何 况.核递推最小二乘辨识算法仿真研究[J].南昌航空大学学报(自然科学版),2011,25(2): 1-6.
LI Zhi-nong,ZHAO Kuang,HE Kuang.Simulation research of kernel recursive least square identification algorithm[J].Journal of NanChang Aviation University (Natural Science Edition),2011,25(2): 1-6.
[10]员险锋.基于非线性输出频率响应函数的转子裂纹故障诊断方法研究[D].郑州:郑州大学,2011.

