考虑行波效应的高墩刚构-连续梁桥地震响应分析

宋晓凯,刘学庆

(上海市浦东新区市政工程建设管理中心，上海200135)

我国幅员辽阔，自然特性相差悬殊，特别是西南山区，地形复杂、山高谷深，在该区域修建铁路不可避免地需要跨越深沟深谷，该种地形铸就了大量的大跨高墩桥梁。近年来，刚构-连续组合梁桥以其突出的跨越能力和无伸缩缝等优点，广泛应用于山区铁路。地震属突发性偶然荷载，它会迫使桥梁结构剧烈振动，桥梁抗震性能的优劣成为了地震时保证整条线路是否安全畅通的关键。文献[1～6]针对各种桥型的抗震性能进行了广泛研究，其研究成果对于我国铁路事业的发展，贡献卓越。然而，这些研究大多针对连续梁桥、连续钢构桥、拱桥等桥型，且大多忽略了地震动的时空变化特性，而针对刚构-连续组合梁桥考虑行波效应的地震响应分析还鲜有报道。

本文以某主跨(48+5×80+48)m的刚构-连续组合梁桥为例，利用ANSYS通用有限元软件，通过大质量法(LMM)求解了行波激励下该结构的非线性地震响应，揭示了行波效应对该种结构地震响应的影响规律。

1 基本理论与计算模型

1.1 大质量法(LMM)

多点激励下，结构的运动方程可表达为[7]：

(1)

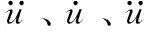
求解式(1)的常用方法[8]有相对运动法(RMM)、大质量法(LMM)和大刚度法(LSM)等。RMM是将结构的地震响应分为拟静力响应和动力响应，然后叠加得到总响应，思路清晰，逻辑推理严密。然而，从本质上讲RMM是基于叠加原理，只适用于线性问题，且对于大型复杂结构需自行编程计算，工作量较大，不便于工程应用。

针对RMM求解大型复杂结构所面临的困境，发展了LMM[6]。LMM首先释放支撑处沿地震波输入方向的约束，并附加一个大质量块M0，通常为结构总质量的106倍。在进行地震响应分析时，通过在支撑处施加等效荷载P(t)=M0Üg(t)来模拟基础运动。LMM通过质量矩阵的置大数，巧妙地将地震荷载输入结构。LMM求解多点激励的运动方程为：

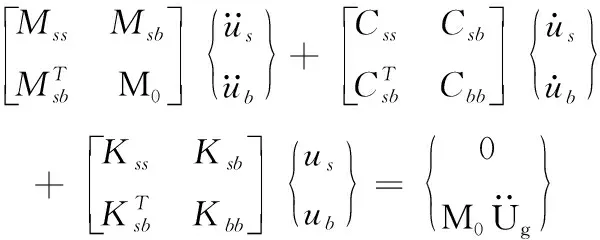
(2)

将上式第2行展开，且考虑集中质量矩阵，可得：

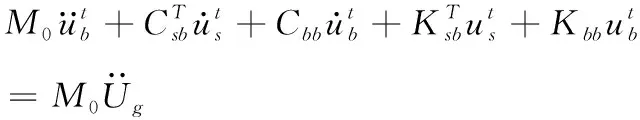
(3)

两边同时乘M0-1，可得：

(4)

在式(4)中，由于M0远大于其它阻尼项和刚度项，则

(5)

式(2)～式(5)即为LMM求解多点激励地震响应的基本原理，它能够方便地利用通用有限元程序来实现，且能够考虑结构的各种非线性特性。

1.2 工程概况

以某典型刚构-连续组合梁桥为分析对象，桥址位于Ⅲ类场地。主桥跨径布置为48 m+5×80 m+48 m，总长496 m。上部结构采用单箱单室变截面箱梁，支点处梁高7.0 m，中跨和边跨端部梁高4.0 m。主梁下部共设置8个桥墩，桥墩高度为65～79 m，其中4#和5#桥墩与主梁固结，而在1#～3#桥墩和6#～8#桥墩墩顶设置活动支座，形成典型的刚构-连续组合梁桥。二期恒载取144 kN/m。结构总体布置图如图1所示。

图1 刚构-连续梁桥立面布置(单位:cm)

1.3 有限元模型

利用ANSYS通用有限元软件建立了该桥的全桥有限元计算模型。主梁和桥墩均采用Beam188空间梁单元模拟，每个节点包含3个线位移和3个角位移。二期恒载等效为质量点，通过Mass21质量单元模拟。刚构墩墩顶与主梁形心固结，活动墩墩顶与主梁形心通过主从自由度连接。不考虑地基刚度的影响，墩底边界按刚性固结处理。结构阻尼比取0.02，时域积分步长取0.01。计算得到结构前4阶自振频率和振型见表1。

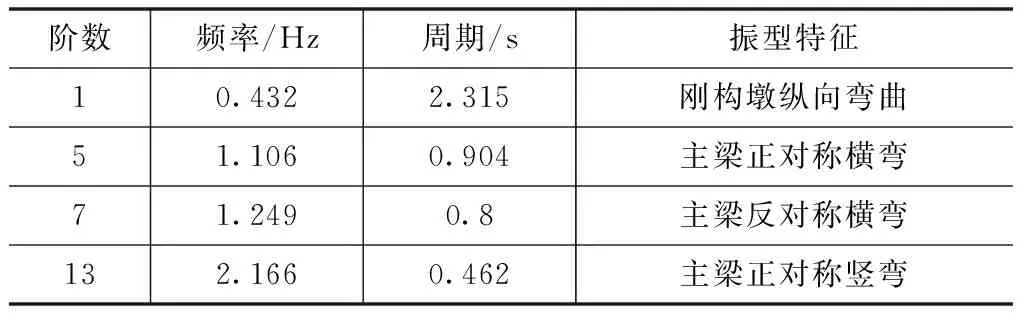
表1 桥梁频率及振型

2 地震波的选取

采用大质量法求解结构的地震响应时，需输入地震波的加速度时程。桥梁结构的地震响应不仅与地震的峰值加速度有关，而且还与地震波的有效持时、场地土性质、场地卓越周期等密切相关。针对该刚构-连续组合梁桥所处的Ⅲ类场[9]，选取两条实际地震波作为输入：1940，El Centro-Imperial Valley，简称El Centro波；1952，Taft-Kern County，简称Taft波。地震记录时间间隔为0.02 s，地震波时程见图2和图3。

图2 El Centro波(1940，270Deg)

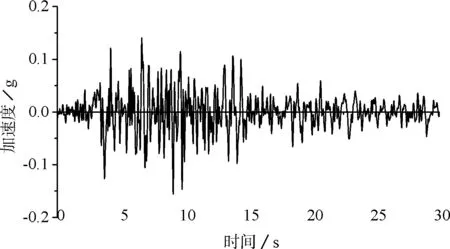
图3 Taft波(1952，69Deg)

对上述地震波进行规格化处理，将其峰值加速度调整为0.1 g，则El Centro波(PGA=0.3569 g)和Taft波(PGA=0.1557 g)的调整系数分别为0.2802和0.6423。假设震源出现在1#桥墩左侧，地震波从1#桥墩向8#桥墩传播。本文只沿纵向输入地震波，为全面考察行波效应的影响规律，分别选取了300、600、900、1 200、1 500、1 800 m/s 6种行波波速分别输入，根据各桥墩之间的间距求得时间延迟量，计算了地震行波输入下桥梁的地震反应。

3 地震响应分析

针对该典型高墩刚构-连续组合梁桥，分别沿纵桥向输入规格化的El Centro地震波和Taft地震波，考虑结构几何非线性的影响，利用ANSYS通用有限元软件，通过大质量法(LMM)求解了结构的非线性地震响应。在纵向地震波作用下，由于活动墩与主梁只有横向和竖向约束，沿纵向可自由活动，因此活动墩表现为单墩振动，可以推测行波效应对活动墩的地震响应无影响。而刚构墩，由于与主梁固结，在地震荷载作用下，根据其刚度比例共同承担地震荷载。因此本研究中重点关注刚构-连续组合梁桥刚构墩(4#墩和5#墩)的地震响应。

3.1 位移响应分析

首先考察行波效应对刚构墩墩顶纵向位移响应的影响规律。对比El Centro波和Taft波分别作用时，一致激励和行波激励(V=300 m/s)两种工况下的墩顶纵向位移时程曲线，如图4和图5所示。

图4 El Centro波作用下5#墩墩顶位移时程

图5 Taft波作用下5#墩墩顶位移时程

由图4和图5可见，考虑行波效应时，刚构墩墩顶的位移时程曲线波形相似，均出现了一定的滞后效应，但不同地震波作用下，刚构墩墩顶的位移时程完全不同。说明，行波效应和地震波频谱特性对刚构-连续组合梁桥刚构墩的位移响应影响很大。

表2给出了行波波速为从300 m/s变化到1 800 m/s时，4#墩和5#墩的墩顶位移与一致激励下的墩顶位移的比值。

表2 刚构墩墩顶位移比值

由表2可见，随着行波波速的增加，4#墩和5#墩的墩顶位移与行波波速并无单调递增或递减的关系，均出现反复波动，且不同地震波作用时，行波效应的影响规律也不相同：El Centro波作用下，4#墩墩顶纵向位移增加，但增幅不大，5#墩墩顶位移减小，但减小量也不大；而Taft波作用下，4#墩和5#墩的墩顶位移均增加，且增幅均较大。因此，不同地震波作用下，行波效应对墩顶位移响应的影响规律不同。

3.2 内力响应分析

考察行波效应对该典型高墩刚构-连续组合梁桥墩顶截面内力响应的影响规律。对比El Centro波和Taft波分别作用时，一致激励和行波激励(V=300m/s)两种工况下的墩顶弯矩、剪力和轴力时程曲线，如图6和图7所示。

由图6和图7可见

(1)与墩顶位移响应相似，考虑行波效应时，墩顶截面的弯矩、剪力和轴力均波形相似，只是在时间上出现了一定的滞后效应；

(2)相同地震动幅值的不同地震波作用下，El Centro波产生的弯矩、剪力和轴力幅值均比Taft波大；

(3)从波形上看，Taft波作用下的弯矩、剪力、轴力时程波动更为明显，说明Taft波的激振频率相比El Centro波更为丰富。

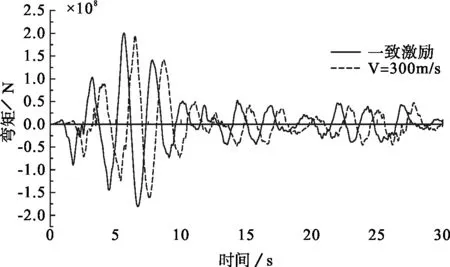
(a)弯矩

(b)剪力

(c)轴力图6 El Centro波作用下5#墩墩顶内力时程

(a)弯矩

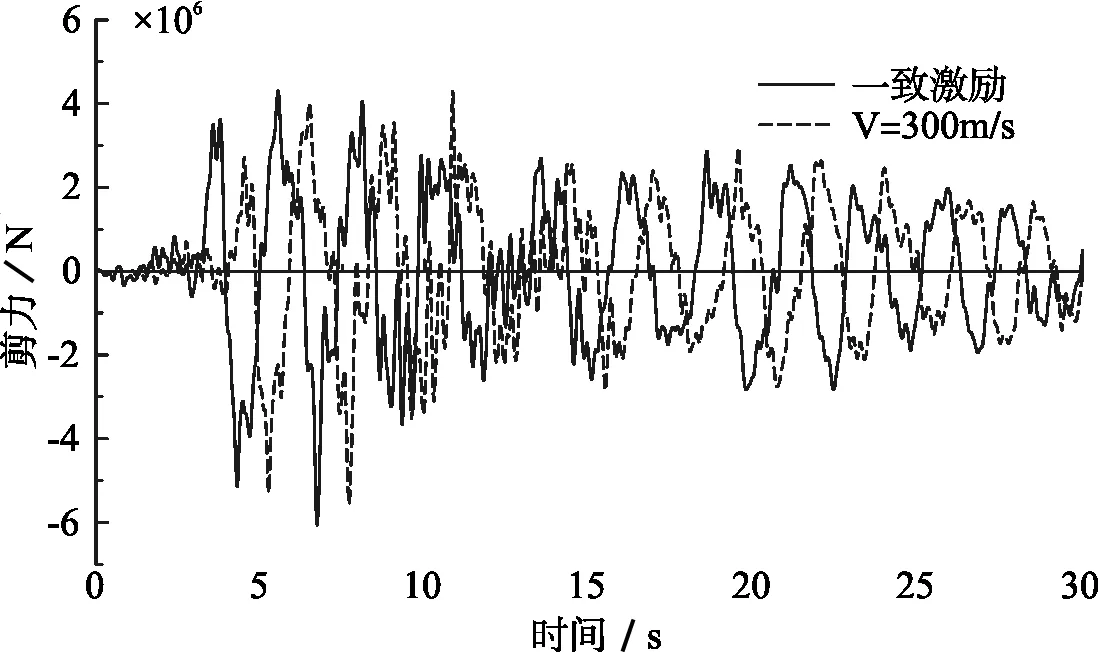
(b)剪力

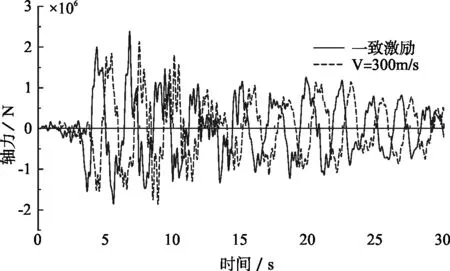
(c)轴力图7 Taft波作用下5#墩墩顶内力时程

表3和表4给出了行波波速从300 m/s变化到1 800 m/s时，4#墩和5#墩墩顶弯矩、剪力、轴力与一致激励输入时的比值。

表3 4#墩墩顶内力比值

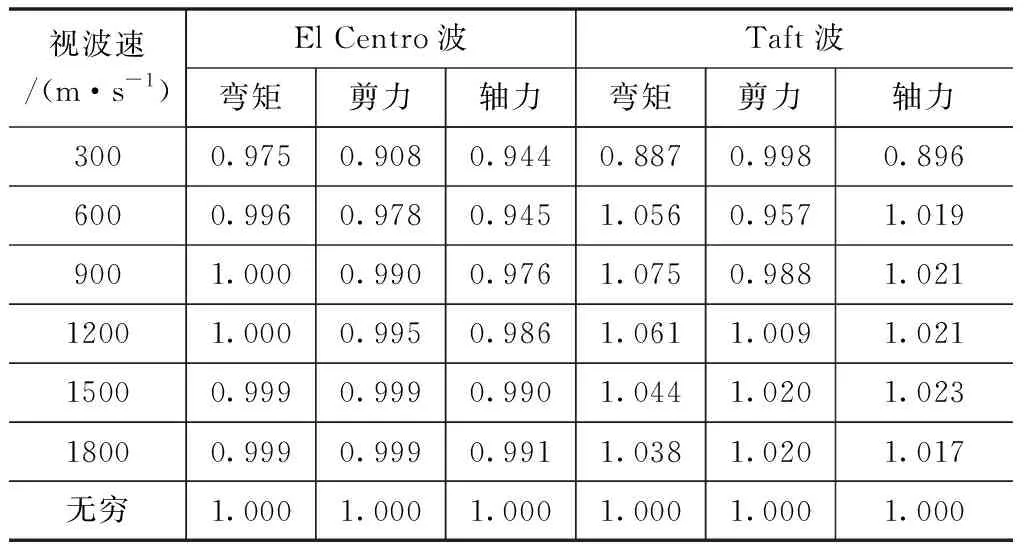
表4 5#墩墩顶内力比值

由表3和表4可见，4#墩墩顶截面的弯矩、剪力和轴力随行波波速的增加出现先增大后减小的趋势，且不同地震波对同一内力指标的影响规律不同，即使相同地震波对不同内力指标的影响规律也不相同。5#墩墩顶截面的内力变化规律与4#墩相似。因此，行波效应对刚构-连续组合梁桥的内力响应影响很大，且对不同指标的影响规律不同。

4 结论

(1)行波效应对刚构-连续组合梁桥活动墩的地震响应无影响，而对刚构墩的地震响应影响很大；

(2)刚构墩的内力响应随行波波速的增加并非呈单调递增或递减的关系。因此，在进行刚构-连续组合梁桥的地震响应分析时，应根据场地类型，选择恰当的行波波速，进行行波激励下的地震响应分析；

(3)相同幅值的不同地震波时程对刚构-连续组合梁桥的地震响应响应影响规律不同。说明，地震动的频谱特性对桥梁的地震响应影响很大，在进行刚构-连续组合梁桥的抗震设计时应选择多条地震样本进行统计分析。

本文只针对行波激励下刚构-连续组合梁桥的纵向地震响应进行了探讨，得出的结论可供该种桥型的抗震性能评估提供参考。而针对该种桥型，考虑行波效应的多维地震响应特点还需进一步研究。

[1] 李小珍，雷虎军. 基于多点激励的刚构-连续组合梁桥行波效应分析[J]. 桥梁建设,2012, 42(6): 33-38

[2] 谢肖礼，王波，张伟峰，等. 罕遇地震作用下高墩连续刚构桥双重非线性抗震分析[J]. 工程力学,2009,26(4):113-118

[3] 李忠献，史志李. 行波激励下大跨度连续刚构桥的地震反应分析[J]. 地震工程与工程振动，2003，23(2)：68-76

[4] Liu A, Yu Q, Zhang J. Seismic response of long span continuous rigid-frame arch bridge[J]. Journal of Shenzhen University Science & Engineering,2007, 24(3)：12-17

[5] 杨庆山，刘文华，田玉基. 国家体育场在多点激励作用下的地震反应分析[J]. 土木工程学报，2008，41(2)：35-41

[6] 刘洪兵，范立础. 大跨桥梁考虑地形及多点激励的地震响应分析[J]. 同济大学学报：自然科学版，2003，31(6)：641-646

[7] 胡聿贤. 地震工程学[M].2版. 北京：地震出版社，2006

[8] 周国良，鲍叶欣，李小军，等. 结构动力分析中多点激励问题的研究综述[J]. 世界地震工程，2009,(4)：25-32

[9] GB 50111-2006铁路工程抗震设计规范(2009年版)[S]