双层分级吸能结构优化设计

董喜文，康国政，朱志武

(西南交通大学力学与工程学院，四川 成都 610031)

随着汽车数量的日益增多以及速度的提高，汽车安全问题受到了广泛关注。汽车在发生正面碰撞时，其前纵梁、翼子板、发动机罩等部件是吸收碰撞能量的主要部件。通过这些部件的变形来吸收碰撞能量及减缓碰撞时的冲击力，从而达到保护乘员的目的。要提高汽车碰撞中的安全性，关键是要提高吸能结构的吸能能力，然而目前提高吸能结构的吸能能力，一般都是通过单纯地增加薄壁管的厚度来增大吸能量。研究表明：当薄壁管的厚度增大时，其比吸能与厚度呈线性关系，初始碰撞峰值力与厚度的二次方呈线性关系，而过大的初始碰撞峰值力将会导致车内人员的“二次碰撞”，造成车内人员的伤亡[1]；当薄壁管的厚度减小时，初始碰撞峰值力会相对减小，但是吸收的能量也会减少，吸能量的减少将会降低汽车的安全性，达不到保护车内人员安全的要求。文献[2]设计了一种八边形的逐级吸能梁，该结构的变形模式是一种高效的渐进叠缩变形模式，在相同的压缩距离下，其吸收的能量较普通结构增大许多，但是研究表明，当吸能梁的截面形状趋近于圆管时，其变形模式的稳定性越差[3]。文献[4]设计了一种切削式吸能装置，该装置利用金属材料被切削产生破坏的原理来耗散碰撞能量，但是该装置对切削刀具有较高的要求。文献[5]设计了一种锥形多胞薄壁吸能结构，系统地分析了结构的长径比、壁厚及锥度对结构比吸能的影响。文献[6-7]分别对多胞薄壁结构进行了优化设计，并得出结构参数的最优解。其比吸能较普通吸能结构有较大提高，但是其初始碰撞峰值力比普通吸能结构大。

如何在提高结构比吸能的同时，又不增大初始碰撞峰值力是本文的主要研究内容。为此，本文提出一种新型的吸能结构，通过有效地调整内外层薄壁管的厚度以及内外层管的长度差，达到增加比吸能的同时又不增大初始碰撞峰值力的目的。同时，将响应面法(RSM)、试验设计(DOE)以及有限元LS-DYNA结合起来，对结构的厚度等因素进行抗撞性优化设计。

1 问题描述

1.1 双层分级吸能结构

汽车在发生碰撞时，其前纵梁、翼子板、发动机罩等前部钣金件是吸收碰撞能量的主要部件，而前纵梁所吸收的能量最多。研究表明，当汽车发生正面碰撞时，前纵梁吸收50%～70%的碰撞能量[8]，因此，提高汽车的抗撞性主要是通过提高前纵梁的耐撞性来实现的。前纵梁主要是通过薄壁管发生塑性变形来吸收碰撞能量，通过发生屈曲来减缓冲击力。当薄壁管壁厚较大时，虽然能够吸收较多的碰撞能量，但是初始碰撞峰值力也会较大，造成车内乘员的“二次碰撞”；当其壁厚较小时，初始碰撞峰值力较小，但是其吸收的能量也会减小，达不到保护车内人员安全的要求。

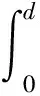
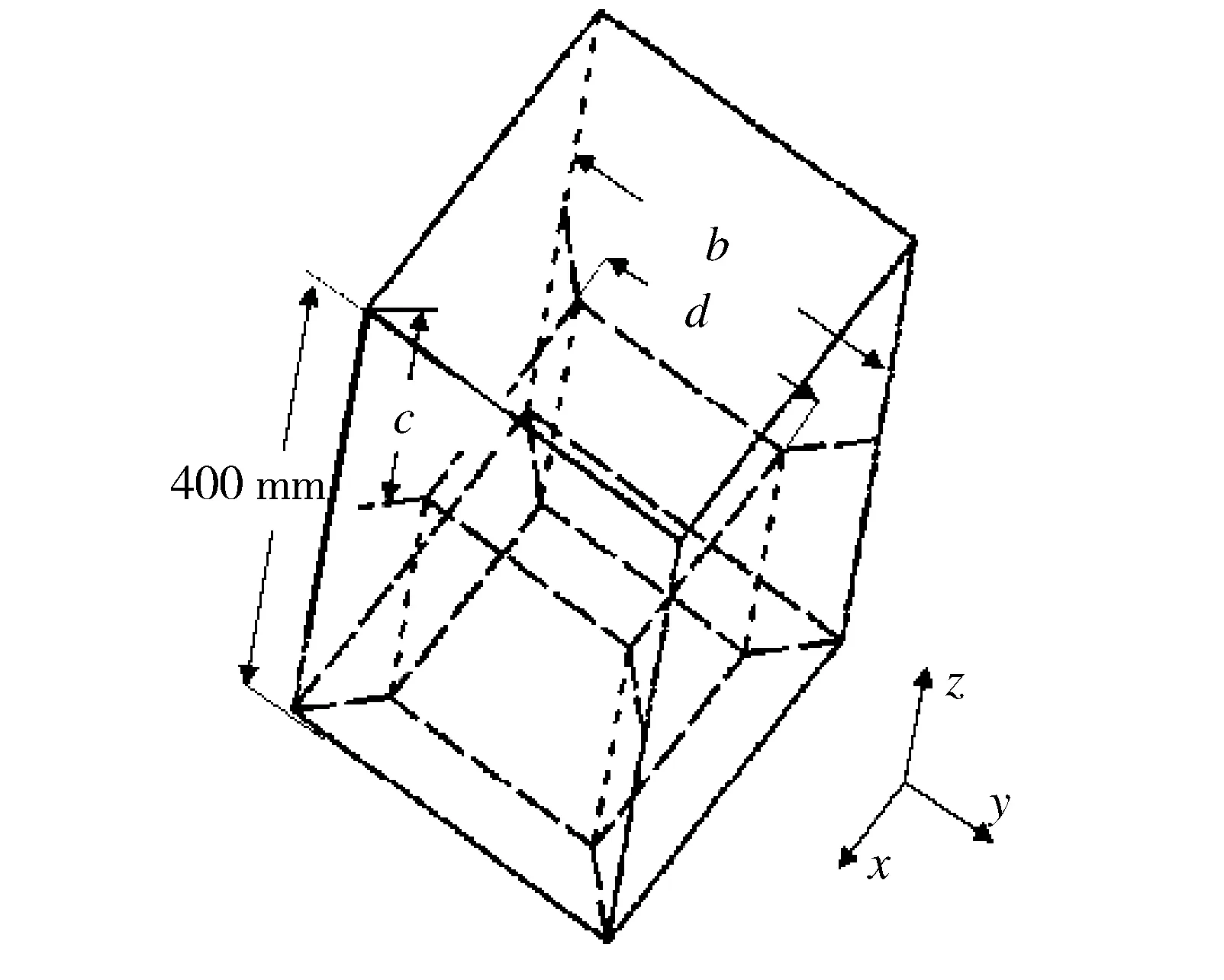
图1 双层分级吸能结构示意图

1.2 吸能结构评价指标

评价吸能结构的好坏主要是通过分析结构的总吸能量、比吸能SEA[9](specific energy absorption)、平均碰撞载荷(mean force)及最大初始碰撞峰值力(maxPL)等。其中，比吸能、平均碰撞力和最大初始碰撞峰值力是衡量结构抗撞性的3个非常重要的分析指标。结构的比吸能越大、最大初始碰撞峰值力和平均碰撞力越小，则其吸能特性越好。比吸能SEA(即单位质量吸收的能量)表示结构在发生碰撞时，材料在能量吸收时的利用率，其表达式为SEA=IntEn/Mass，其中IntEn为结构所吸收的总能量，Mass为结构的总质量。初始碰撞峰值力是结构刚发生屈曲，形成结构的初始叠缩时所对应的碰撞力。在普通吸能结构中，初始碰撞峰值力是整个叠缩过程中所有峰值的最大值，前纵梁的壁厚越大则初始碰撞峰值力越大。

2 有限元分析

利用三维建模软件Pro/E建立双层分级吸能结构的几何模型，将几何模型保存为igs格式再导入到Hypermesh进行网格划分，采用大变形Belytschrko-Tsay四节点壳单元。考虑到模拟精度的要求，在薄壳单元的厚度方向上取3个积分点，面内采用减缩积分，单元长度设为4 mm，内外层薄壁管的厚度均设为2 mm。将内层管与4块薄板设为part1，外层管设为part2。考虑part1与part2在碰撞时会发生相互接触及自身接触，采用自动单面接触算法进行模拟，并考虑接触面之间的摩擦。约束结构z=0处节点的所有自由度，在双层分级吸能结构的上方z=401 mm设置一刚性墙，质量为400 kg，以10 m/s的速度去撞击吸能结构。有限元模型如图2所示。

图2 双层分级吸能结构有限元模型

双层分级吸能结构采用AA6061-T4[10]铝合金材料，其密度ρ0=2.7×103kg/m3，弹性模量E=70 GPa，泊松比v=0.28，屈服应力σy=110 MPa，应力-等效应变曲线如图3所示。由于AA6061-T4铝合金材料对应变率不敏感，因而采用LS-DYNA中MAT24多段线性模型来模拟其力学响应。

图3 AA6061-T4应力-等效塑性应变曲线[10]

为了体现新型吸能结构在比吸能及初始碰撞峰值力上的优势，对新型吸能结构和普通吸能结构的比吸能及初始碰撞峰值力进行比较分析，如图4—5所示。图中，PC为普通吸能结构，其尺寸为100 mm×100 mm×400 mm；ST75-0为双层吸能结构，外层管边长为100 mm，内层管边长d=75 mm，内层管与外层管的长度差c=0；ST75-50为双层分级吸能结构，内层管边长d=75 mm，内层管与外层管的长度差c=50 mm。从图4可以看出，在Dis=225 mm处，PC的比吸能为7.538 kJ/kg，ST75-50的比吸能为10.997 kJ/kg，ST75-0的比吸能为11.879 kJ/kg。PC吸能结构的初始碰撞峰值力为93 kN；ST75-50吸能结构的初始碰撞峰值力为101 kN；ST75-0吸能结构的初始碰撞峰值力为181 kN。

图4 双层吸能结构、普通吸能结构的比吸能

双层吸能机构、普通吸能机构比吸能及峰值力如表1所示。可知：ST75-50新型吸能结构在初始峰值力只增加8.8%的情况下，比吸能提高了46%；ST75-0双层吸能结构在初始峰值力增加了94%的情况下，比吸能却只提高了58%。进一步分析可知，ST结构比吸能比PC结构高的原因是：1)在单位距离内新型ST结构所产生的塑性铰比PC结构多，而塑性铰越多，结构的吸能量也就越多；2)新型ST结构又是一种双层结构，在碰撞过程中内外层管之间会发生摩擦，而层管之间的摩擦也会消耗部分碰撞能量。需要指出的是，ST75-0初始碰撞峰值力过大是由于z=0处的轴向刚度过大导致的。另外，虽然ST75-50的比吸能提高了，但其峰值力却并未增大很多。这主要是因为在ST75-50结构的前半段(即单层部分)，其轴向刚度与PC结构相差不大。

表1 双层吸能结构、普通吸能结构比吸能及峰值力

注：ΔSEA=[SEA(ST)-SEA(PC)]/SEA(PC);ΔF=[F(ST)-F(PC)]/F(PC)。

3 双层分级吸能结构优化设计

以结构的比吸能、初始碰撞力为优化目标函数，分析结构各参数对结构的比吸能及初始碰撞峰值力的影响。以结构的外层壁厚t1、内层壁厚t2、内层宽度d及内外层长度差c为设计变量因子X=[t1t2dc]T，则结构的比吸能、初始碰撞峰值力的二次响应面函数为：

(1)

(2)

式中，a=(a1,a2,a3,...,a15)T和b=(b1,b2,b3,...,b15)T是关于响应面函数的待定系数，其值可由有限元分析结果代入式(1)、式(2)求得，则SEA和Fmax的数学优化设计模型为：

(3)

(4)

由于设计变量因子在设计空间中有无数种组合方式[11]，对所有组合进行逐一分析是不现实的；因此，本文采用一种组合式优化设计思路，即将试验设计(DOE)、有限元分析(FEA)和响应面法(RSM)按照一定的顺序组合起来，进而求解出双层分级吸能结构的优化问题。其中，响应面法(RSM)的基本思想是通过构造一个近似模型来描述目标函数与设计变量因子之间的关系[12]。

本文的多目标优化问题可以表示为

(5)

式中：f1=SEA(x)/SEAmax,为比吸能的量纲—函数[7]，SEAmax为约束条件下最大值；f2=F(x)/Fmax,为初始碰撞峰值力的无量纲函数，Fmax为约束条件下最小值。由于比吸能SEA所求的为最大值，而初始碰撞峰值力F为最小值；因此,在进行多目标函数优化前，需要将比吸能SEA转为求最小值，亦即在比吸能SEA响应面函数前加上一个负号，从而将整个多目标优化函数转化为求函数的最小值。w为权重系数，体现了各优化目标在整个多目标优化函数中的重要程度。由于比吸能是本文的首要考虑因素，初始碰撞峰值力的重要性相对较小，在这里将比吸能的权重系数设为0.7，初始碰撞峰值力的权重系数设为0.3。

为了求解式(1)、(2)中的待定系数，采用5因素4水平的正交实验表L16(45)来进行正交试验，共设计了17组试验数据。第17组试验是全面考虑各因素之间的交互作用而增加的一组数据。正交试验各因素水平的取值及其有限元模拟结果如表2所示。

表2 正交试验分布及试验数据

将表2的SEA及Fmax代入式(1)、(2)，利用最小二乘法求得待定系数a和b，并解出SEA和Fmax响应面函数在约束条件下SEA的最大值、Fmax的最小值。由于SEA和Fmax在数值上不是一个量级的，因此在进行多目标优化前，对2个响应面函数进行无量纲处理。将2个无量纲函数代入式(5)便可求得多目标函数的最优值，优化结果如表3所示。

表3 多目标优化结果

将优化后的结果与PC普通吸能结构的比吸能及初始碰撞峰值力进行比较，如表4所示。双层吸能结构通过改变外层薄壁管的厚度来控制结构的初始碰撞峰值力，同时改变内层管的厚度来提高结构的比吸能。这种结构能够有效地通过控制厚度达到控制比吸能及初始碰撞峰值力的目的。双层吸能结构的初始碰撞峰值在减小10%的情况下，其比吸能提高了92.4%，极大地提高了结构的吸能。对于优化后结构的加速度，计算结果表明结构的最大加速度不超过45g，平均加速度为30g，根据人体头部伤害指标，加速度满足汽车安全设计要求。

表4 优化后的ST与PC普通吸能结构比较

注：ΔSEA=[SEA(ST)-SEA(PC)]/SEA(PC);ΔF=[F(ST)-F(PC)]/F(PC)。

4 结论

本文通过分析各种组合结构的吸能特性，提出一种双层分级吸能结构，并对其碰撞特性进行数值模拟，模拟结果显示该结构具有良好的比吸能及较低的初始碰撞峰值力。同时，以该结构的外层壁厚、内层壁厚及宽度、内外层长度差为设计变量，结合正交试验设计及LS-DYNA有限元分析对结构进行了优化。优化过程中通过响应面法，建立了双层分级吸能结构的比吸能及初始碰撞峰值力与设计变量间的函数关系。同时，还建立了比吸能和碰撞力的多目标函数，并采用Matlab求解出结构的最优解。优化结果表明，在满足汽车安全设计的条件下，新型吸能结构的比吸能及初始碰撞峰值力都比普通吸能结构有很大的提升。

[1]贾宇．机车车体耐碰撞结构设计与碰撞仿真研究[D]．成都：西南交通大学，2005．

[2]曹立波，崔崇桢，白中浩，等．八边形逐级吸能梁的设计与优化[J]．湖南大学学报，2010，37(1)：29-34.

[3]张涛，刘土光，肖汉林，等．高速冲击下薄壁组合结构吸能特性研究[J]．爆炸与冲击，2006，26(5)：395-403.

[4]雷成，肖守讷，罗世辉．轨道车辆切削式吸能装置吸能特性研究[J]．中国机械工程，2013，24(2)：263-267.

[5]亓昌，董方亮．锥形多胞薄壁管斜向冲击吸能特性仿真研究[J]．振动与冲击，2012，31(24)：102-107.

[6]侯淑娟．薄壁构件的抗撞性优化设计[D]．长沙：湖南大学，2007.

[7]陈仙燕．薄壁构件与桁架结构的抗撞性优化研究[D]．长沙：湖南大学，2007.

[8]McNay I I，GENE H．Numerical Modeling of Tube Crash with Experiment Comparison[R]．SAE，880898，1988：22-24．

[9]Kim H S．New Extruded Multi-cell Aluminum Profile for Maximum Crash Energy Absorption and Weight Efficiency[J]．Thin-Walled Structures，2002，40：311-327．

[10] Chen W G，Wierzbicki T．Relative Merits of Single-cell，Multi-cell and Foam-filled Thin-walled Structures in Energy Absorption[J]．Thin-Walled Structures，2001，39：287-306．

[11]武和全，胡宏伟，辛勇．薄壁梁诱导槽结构抗撞性优化设计及应用[J]．公路交通科技，2011，28(1)：120-126．

[12]Khuri A I，Mukhopadhyay S．Response Surface Methodology[J]．Wiley Interdisciplinary Reviews: Computational Statistics，2010，2(2)：128-149．