标准模型下2种基于身份的环签名的安全性分析

周强胜,李 虓,何明星,杜亚军

(西华大学数学与计算机学院,四川 成都 610039)

1984年，Shamir[1]首先提出基于身份的公钥密码机制。在该机制中，用户的身份信息(如身份证号码、家庭住址等)作为用户的公钥，用户的私钥由私钥生成中心(PKG)生成，从而有效地解决了传统公钥体制下的公钥证书的管理和运算的问题。

随着电子商务、电子政务的广泛应用，用户的隐私保护越来越受到重视。环签名是一种保护签名者隐私的密码学原语。2001年，Riverst等[2]首次提出环签名概念。因为环签名的签名有一定的规则性且类似于环状，故命名为环签名。通过环签名技术，合法的签名者可以不征求环中其他成员的同意而随机地选择环成员，并用自己的私钥和其他环成员的公钥对选择的任何消息进行签名。验证者可以验证环签名的有效性，但是不能确定具体签名者的身份。和群签名相比较，环签名没有群管理员，没有组织过程和撤销程序，而且签名者的身份是无条件匿名的。

2002年，Zhang等[3]首次利用双线性对构造了基于身份的环签名方案； 2006年，Au等[4]提出了标准模型下基于身份的环签名方案，并给出了相应的安全性证明。2008年，张跃宇等[5]改进了文献[4]的方案并提出了一种新方案，该方案在通信和计算效率上有较大提高。同年，王化群等[6]发现文献[4]提出的方案是不安全的，并给出了2种攻击方法及改进方案。2009年，刘振华等[7]在文献[4-5]的基础上，提出一种新的标准模型下基于身份的环签名方案，该方案在通信和计算效率上也有较大提高，但依然不安全。程文华等[8]对文献[5]提出的方案进行了攻击并给出了改进方案。改进方案虽然在安全性上有所提高，但在验证时双线性对的运算与环成员的个数成正比，计算效率较低。2012年，葛爱军等[9]提出一种标准模型下固定长度的基于身份的环签名方案，该方案只需要3个双线性对运算，占用通信带宽低，计算效率较高。

文献[8]声称他们的改进方案在环签名的最强安全模型下是安全的；文献[9]也声称他们的方案能抵抗适应性选择消息的伪造攻击。本文对文献[8-9]中的环签名方案的安全性进行密码学分析后发现，文献[8]的方案不能抵抗存在性伪造攻击，文献[9]的方案不能抵抗多已知签名存在伪造攻击和环成员改变伪造攻击。本文给出具体的伪造攻击方法来说明文献[8-9]的方案不满足环签名的不可伪造性。

1 预备知识

1.1 双线性对

双线性对[10-12]是指具有下列性质的一个映射：e:G1×G1→G2(假设G1和G2是2个阶为素数p的乘法循环群，G1的一个生成元是g)。

1)双线性：对任意的a,b∈Zp，所有的g1,g2∈G1，有e(g1a,g2b)=e(g1ab,g2) =e(g1,g2ab)=e(g1,g2)ab。

2)非退化性：存在g1∈G1，使得e(g1,g1)≠1。

3)可计算性：对所有的g1,g2∈G1，存在有效的算法来计算e(g1,g2)。

1.2 环签名模型(基于身份)

该模型主要由4种算法组成。

1)系统建立阶段：PKG输入安全参数∂，输出系统参数Params以及主密钥k。PKG 保密主密钥k，公开系统参数Params。

2)私钥生成阶段：PKG输入系统参数Params、用户的身份Ij以及主密钥k，输出用户身份Ij以及用户对应的私钥sj，并将用户的私钥sj安全地发送给用户。

3)签名阶段：用户输入系统参数Params、用户身份R、私钥sj和待签消息M，输出R关于M的环签名σ。

4)验证阶段：验证者输入系统参数Params、用户身份R、已签消息M和环签名σ，输出1或0。

1.3 环签名的不可伪造性安全模型

该模型主要分为3类[9]：Model1、Model2和Model3。从Model1到Model3它们的安全性是依次增强的。 Model1忽略了环成员的改变攻击和多已知签名存在伪造攻击的情况； Model2虽然将环成员的改变攻击考虑在内，但是忽略了多已知签名存在伪造攻击的情况； Model3将这2种攻击方法都进行了考虑。

2 G-M-ZH-CH方案及其安全性分析

2.1 G-M-ZH-CH方案

2012年，葛爱军等[9]提出一种标准模型下固定长度的基于身份环签名方案，这里简记为G-M-ZH-CH方案。其具体描述如下。

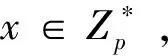
签名算法：令R={ID1,ID2,…,IDk}为环签名中所包含的k(k≤n)个身份列表，假定真实签名者身份为IDs(s为1,2，…,k中的任意一位成员)，对消息M=(M1,M2,…,Mm)∈{0,1}m进行签名如下。

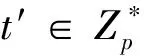
3)输出对消息M的签名σ=(σ1,σ2,σ3)。

2.2 G-M-ZH-CH方案的安全性分析

G-M-ZH-CH方案[9]声称该方案安全性强，对适应性选择消息攻击是存在性不可伪造的，但通过分析，笔者发现该方案并不满足环签名的不可伪造性。G-M-ZH-CH方案在构造时忽略了多已知签名存在伪造攻击以及环成员的改变攻击等情况。在双线性计算n-DHE困难问题假设下，G-M-ZH-CH方案给出了存在性不可伪造证明，但其安全模型并没有考虑到这2种攻击。这就导致了虽然方案的不可伪造性证明可以规约为在双线性计算n-DHE困难问题假设下，但实际上该方案仍不能抵抗多已知签名存在伪造攻击和环成员的改变伪造攻击。攻击者在得到消息M的环签名后可以伪造出该消息的新的环签名，以及一个环成员可以对任意消息生成一个不包含自己环的环签名。下面给出这2种具体伪造攻击方法。

攻击方法1：G-M-ZH-CH方案不能抵抗多已知签名存在伪造攻击，即任何一个攻击者在得到环R关于消息M的环签名σ=(σ1,σ2,σ3)后，可以按照如下方法进行伪造攻击。

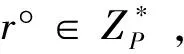
显然,这个伪造的签名是合法的。这是因为

3 CH-W-H方案及其安全性分析

3.1 CH-W-H方案

2009年，程文华等[8]提出一种改进的标准模型下的基于身份的环签名方案，这里简记为CH-W-H方案。其方案具体描述如下。

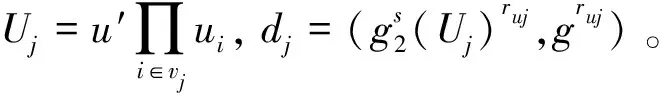
4)计算h=Hm(R,m,R1,R2,…,Rn)，S=

5)环R对消息m的环签名为σ=(S,R1,R2,…,Rn)。

3.2 CH-W-H方案的安全性分析

攻击者在得到环R关于消息m的签名σ=(S,R1,R2,…,Rn)的情况下，都可以伪造该环对任何消息m′的签名。具体的伪造攻击如下。

1)攻击者得到环R关于消息m的签名σ=(S,R1,R2,…,Rn)后，计算h=Hm(R,m,R1,R2,…,Rn)。

4 结束语

一种安全的环签名方案必须满足正确性、无条件匿名性、不可伪造性等属性。本文对2种标准模型下基于身份的环签名方案的安全性进行了详细分析，发现它们不满足环签名的不可伪造性，并给出了相应的攻击方法。本文主要考虑了3种伪造攻击方法： 1)攻击者在不改变环成员和消息情况下的伪造攻击； 2)攻击者在不改变环成员的情况下，改变消息的伪造攻击； 3)环中合法的用户选择一个不包括自己的环并对任意消息的伪造攻击。提出一些新的能克服上述攻击方法的标准模型下的环签名方案，将是未来研究工作的重点。

[1] Shamir A. Identity-based Cryptosystems and Signature Schemes [C]// Advances in Cryptology-CRYPTO’ 84, LNCS196. Berlin: Springer-Verlag, 1984: 47-53.

[2] Riverst R L, Shamir A, Tauman Y. How to Leak a Secret [C]//Advances in Cryptology ASIACRYPT 2001, LNCS 2248.Berlin: Springer- Verlag, 2001:552-565.

[3] ZHANG F, KIM K. ID-based Blind Signature and Ring Signature from Pairings[C]//Advances in Cryptology-ASIACRYPT 2002，LNCS 2501．Berlin：Springer-Verlag，2002：533-547．

[4] AU M H ，LIU J K，YUEN T H，et al．ID-based Ring Signature Scheme Secure in the Standard Model[C]//IWSEC 2006: The First International Workshop on Security, LNCS 4266. Berlin: Springer-Verlag. 2006: 1-16．

[5] 张跃宇，李晖，王育民．标准模型下基于身份的环签名方案[J]. 通信学报, 2008, 29(4):40-44.

[6] 王化群，于红，吕显强．两个标准模型中可证安全的环签名方案的安全性分析及其改进[J]. 通信学报, 2008, 29(8):57-62.

[7] 刘振华，胡予濮，牟宁波,等．新的标准模型下基于身份的环签名方案[J]．电子与信息学报，2009, 31(7): 1727-1731.

[8] 程文华，王彩芬，韩亚宁,等．改进的标准模型下的基于身份的环签名方案[J]．计算机应用研究，2009, 26(11): 4286-4288.

[9] 葛爱军, 马传贵, 张振峰, 等. 标准模型下固定长度的基于身份环签名方案[J]. 计算机学报,2012, 35(9)1874-1880.

[10] LIU J K,WONG D S. On the Security Models of (threshold) Ring Signature Schemes [C]//ICISC2004. Berlin: Spinger-Verlag, 2004, 204-217.

[11] MASSYUKI A B E,OHKUBO M SUZUK K.1-out-n Signatures from a Variety of Keys [J]. IEICE Trans Fundamentals, 2004, E87-A, 131-140.

[12]李伟，唐明伟，范明钰.标准模型下基于线性的选择关联可转换环签名方案[J].西华大学学报：自然科学版，2013,32(2)：1-4.