一种运用相位差测量标签距离的方法
(西华大学电气信息学院,四川 成都 610039)
无源标签有体积小、存储容量大、成本低等特点,在仓储、交通、物流等领域使用越来越广泛[1];但是由于标签设计水平的局限和各种未知干扰源的广泛存在,目前900 MHz 频段的无源RFID标签应用存在较多问题,如识别距离不够和误码率相对较高。误码率往往会随着标签与阅读器距离的增加呈指数上升,故仍可归结为实际有效识别距离较小的问题[2]。
RFID系统是利用电磁波反射进行从标签到阅读器的数据传输[3]。传统的标签距离测量的方法有RCS计算法[4]和福利斯空间公式计算法[5]等。这些方法的共性是要考虑电磁波从发射到反射回来时的各种影响, 计算繁琐,未知量较多,实际操作也不方便。基于此,本文提出一种计算快、操作方便的相位差测量方法。
1 测量原理
1.1 相位差测距原理
相位差测距的原理如图1所示,由阅读器在正常读写时对标签发射一个电磁波信号,然后再接收标签反射回来的信号,阅读器通过测量该电磁波信号往返经过的时间,计算出阅读器与无源标签之间的距离[6-8]。

图1 阅读器至标签数据传输及相位测距框图
图1中:Δφ为最后测量得到的相位延迟;Δφ1为信号传递过程中的延迟相位;Δφ2为标签内部电路产生的相位延迟;τ是阅读器到标签的信号传输时间。其中
Δφ1=2πf0·τ
(1)
式(1)中f0是发送的载波频率。当信号从阅读器发送至标签,再由标签反射回阅读器时,测得总的延迟相位差为
Δφ=2Δφ1+Δφ2
(2)
设光速为c,可以得出阅读器到无源标签的距离
d=cτ
(3)
无源标签是通过电磁耦合的形式供电[3],故图1中标签内部可等效为一个并联谐振回路,电路产生的相位差
Δφ2=-arctan([ωC-(1/ωL)]/(1/R))
(4)
式中:R、L、C是无源标签内部等效谐振回路的电阻、电感和电容;ω=2πf0是发送的载波角频率。
由并联谐振回路的特质[9]可知,一般情况下,R≤ωL时,并联阻抗|Z|和品质因数Q的表达式为:
(5)
(6)

1)假设随着回路损耗电阻R值的减小,由式(6)、式(5)知,Q值将减小,回路阻抗|Z|越小,相对应的,回路产生的相位延迟Δφ2会增加;再由式(2)和式(4)知,标签测距时,测量回路总的相位延迟Δφ减小,从而降低了测量精度。
2) 当回路谐振ωC=1/(ωL)时,并联回路中只有回路损耗电阻R,此时谐振回路产生的相位延迟Δφ2为0,测量回路总的相位延迟Δφ增加,从而提高了测量精度。
3)当回路损耗电阻R值越大时,Q值将越大,回路阻抗|Z|会增加,因此回路产生的相位延迟Δφ2会减小。由式(2)和式(4)知,测距时,测量回路总的相位延迟Δφ增加,从而提高了测量精度。
1.2 相位差测距分析
如果采用单一的频率进行测量,由式(2)可知,信号传递过程中的相位延迟可以用式(1)得到;但是标签内部回路产生的相位差是无法预知的,即使可以根据式(4)来求解。在实际测量时,构成谐振回路的主要元件电阻R、电感L和电容C这3个量是未知,以至于无法精确地计算出信号在标签内部的损耗,所以可以采用一个辅助的频率来测量[6],则有:
Δφ(fi)=2Δφ1(fi)+Δφ2(fi)
(7)
Δφ(fj)=2Δφ1(fj)+Δφ2(fj)
(8)
在一定的频段范围内,相邻2个发射频率fi和fj非常接近时,标签内部的相位变化很小,基本上可以视为Δφ2(fi)和Δφ2(fj)是相同的[7],所以公式(7)和(8)相减得到
Δφ(fi)-Δφ(fj)≈2Δφ1(fi)-2Δφ1(fj)
(9)
将式(1)代入式(9),整理后得到
Δφ(fi)-Δφ(fj)≈4π·Δf·τ
(10)
其中,Δf=fi-fj,fi、fj的变化范围为800~1000 MHz。
将式(10)代入式(3)中,整理后得到测量距离的表达式
(11)
由式(11)可知,实际测量时,在一定条件下可以不用考虑标签内部相位差的变化,只考虑频率Δf的变化和频率的起始点位置。
通常在采用信号能量来计算标签距离时,由文献[4]和文献[5],得到距离公式:
(12)
(13)
式中:Gr是阅读器天线的增益;Pr是发射功率;Gt是标签天线的增益;p为极化损耗;PtagTH是标签激活功率;τ系统传输功率;Pmin阅读器接受信号的灵敏度;λ是电磁波波长;RA和ZA+ZT是标签天线和内部芯片的回路损耗电阻和阻抗。
通过式(11)、式(12)和式(13)3个计算距离公式对比可知:使用式(11)计算标签距离最为简单,里面只包含2个未知量,分别为相位差和频率差;使用式(12)和式(13)计算时,含有的未知量较多,计算比较繁琐,且容易出错。
1.3 理论建模分析
对考虑标签内部延迟和不考虑标签内部延迟2种情况在MATLAB中建模,以进行理论验证并确定频率差的选取范围。
假设已知无源标签内部R=33 Ω,ωL=112[8],其中ω=2πf。若标签谐振频率f=915 MHz,有L=1.9481×10-8Hz,且由ωC-(1/(ωL))=0, 则有C=1.553×10-12F,信号传输时间τ=d/c=4.5×10-10s(其中c=3×108m/s,阅读器与标签距离d=0.135m)。由式(2)得到
(14)
在谐振频率f=915 MHz时,代入式(14)可得Δφ=5.1742,同理可以得到在800~1000 MHz范围内各频率点的相位差。
1)当起始频率固定,f1=800 MHz,Δf=fj-f1(其中fj的取值范围为800~1000 MHz)分别以10、20、30、40 MHz等顺序变化时,式(14)在2种情况下的相位差变化如图2(a)所示。
2)当起始频率fi以一定的规律增加,即Δf=fj-fi=10 MHz(其中fj、fi取值范围为800~1000 MHz,且fj>fi)保持不变时,式(14)在2种情况下相位差的变化如图2(b)所示。

图2 式(14)相位差与频率差和起始频率fi的关系
从图2(a)可以看出,在本仿真所设定的标签参数R、L、C情况下,随着Δf的增加,考虑标签内部延迟和未考虑标签内部延迟时的相位差在900~950 MHz这段频率范围内,基本是相等的,所以运用这段频率进行测量时,克服标签内部延迟的效果最佳,测距精度也相对更高。图2(b)也得出了相同的答案:运用式(11)进行实际测量时,可以采用这段范围内的频率,使标签内部延迟对测量精度的影响较小。
3) 假设频率差的变化范围为1~100 MHz,根据式(14)计算出在这个范围内所包含频率的相位差,再由式(10)计算时延估计误差,其结果如图3所示。

图3 时延估计误差与频率差的关系
从图3可以看出:只有频率差为1 MHz时,时延估计误差是最小的;当频率差大于1 MHz时,时延估计误差随着频率差的增加而增加,到最后无论频率差如何变化,误差都达到了一个恒定值,在这种情况下运用相位差测量标签距离是毫无意义的。由此可以确定,在实际测量时,相邻2个频率之差选择为1 MHz时,测量效果最佳。
2 实验验证
本文采用九州JZURA21阅读器进行实验。测量时阅读器与无源标签之间的距离d设定为13.5、35、38、40、43 cm,对阅读器的接收信号与阅读器本振混频和低通滤波后的 I/Q 2路输出进行数据采集。采集得到的数据使用MATLAB仿真软件将波形显示出来,且将2路信号的数据相比,取反正切,得到1组全新的数据,再求其平均值,最后得到的数据即为信号在阅读器和标签之间传递时的相位延迟。
测量时固定距离d分为小于1个电磁波波长和超过1个电磁波波长2种情况。测量不同频率在该位置时信号往返传输的相位差,由此根据式(10)计算出传输时间τ,再由式(11)计算出测量距离,从而得到测量误差。由于求取相位延迟时用到了反正切函数,故得到的相位差测量值应在(-π/2,π/2)之间。
测量时频率设定为917.7、918.7、919.7、920.7、921.7、922.7、923.7、924.7、925.7、926.7 MHz10个频率。以1 MHz频率差间隔进行数据采集,处理每个频率点从示波器采集到的数据,最后得到电磁波波形图和相位图。以频率917.7 MHz、d=13.5 cm为例说明该实验的整个处理过程。图4分别是该频率的I/Q 2路信号的波形图和相位图。

图4 频率917.7MHz下得到的波形图和相位图
从图4可以看出,采集得到的数据中有很多值超过了所要求的范围(-π/2,π/2)。其主要原因是求取相位时出现了与零相比的奇异点。为此,采用2种方法处理:一种是直接取图4中的I/Q 2路信号相对平稳的一段,求取相位的平均值;另一种是将图4中I/Q 2路信号中的一些奇异点剔除掉,重新组合得到一组新的数据,再求取其平均值。图5是图4相位图中一个稳定段的相位图;图6是剔除奇异点后的I/Q 2路信号的波形图和相位图。
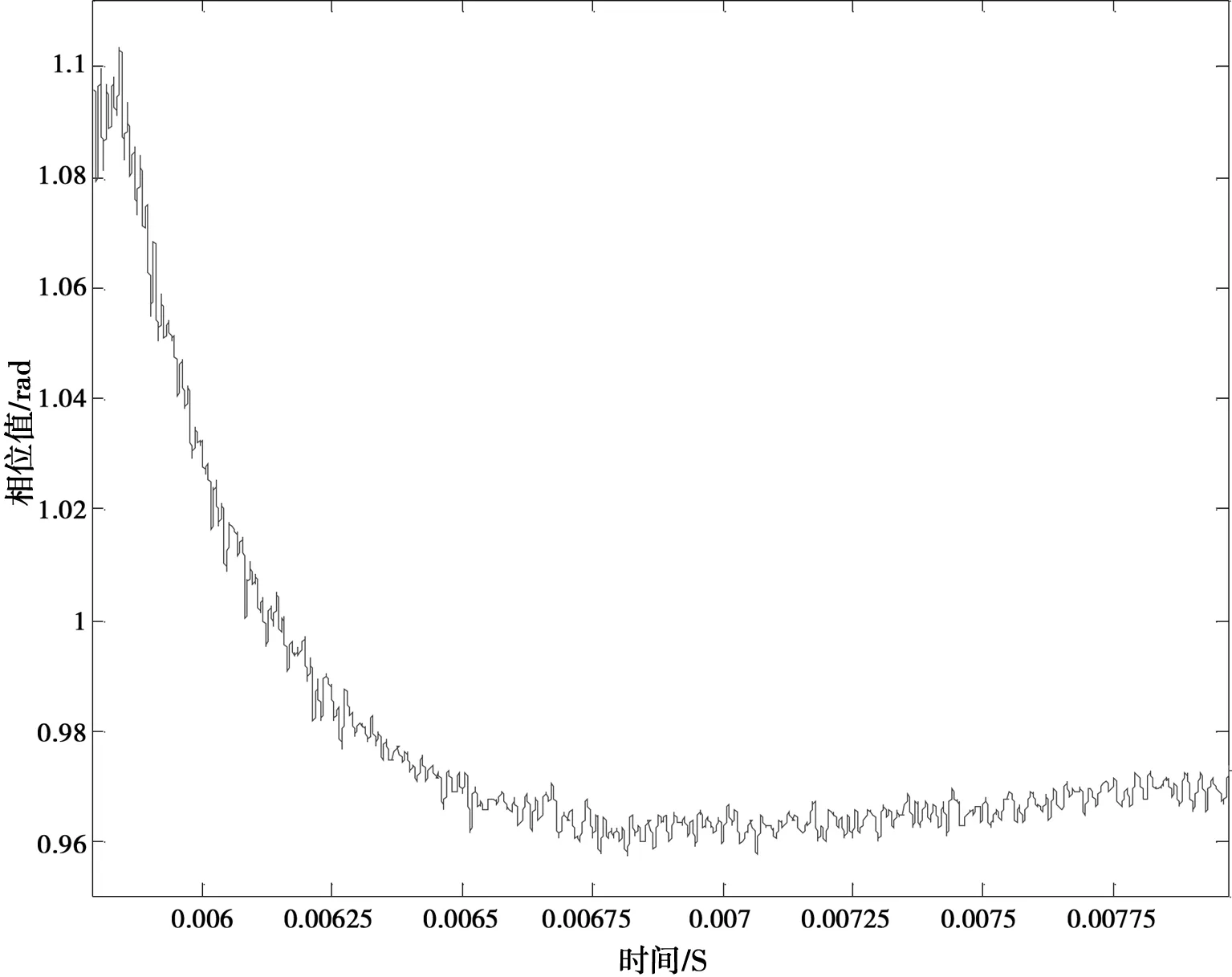
图5 取稳定段得到的相位值

图6 剔除奇异点后的波形图和相位图
图5和图6中的相位图,分别是2种处理方法下得到的结果,都符合测量所要求的范围。在频率917.7 MHz下测量得到的相位差平均值分别为0.966 3和0.991 68。其他的频率点也可以仿照频率917.7 MHz的步骤进行数据处理,最后得到1个波长内测量的相位差值,如表1所示。

表1 频率在几种情况下的相位差值(d=13.5cm在1个波长内)
对表1中的数据处理,运用式(11)求解出每个频率相对应的测量距离,进而得到1个波长内实际距离与测量距离之间的误差。图7给出了3种数据处理情况下的结果。

图7 3种不同处理方式数据情况下传输距离误差
从图7可以看出,测量距离在1个波长内,数据不以任何方式处理时,测量误差最大,而将数据进行取稳定段或剔除奇异点后,测量误差都较小。由此可知,用后2种数据处理方式,且不计测量环境的影响时,克服标签内部延迟的效果最好,测量误差都在6%之内。
当测量距离超过1个波长甚至多个波长时,仍然采用上面所运用的方式来进行数据的采集及处理。对比不同距离下,测量距离与实际距离之间的误差,得出相应的结果,测量数据如表2所示。
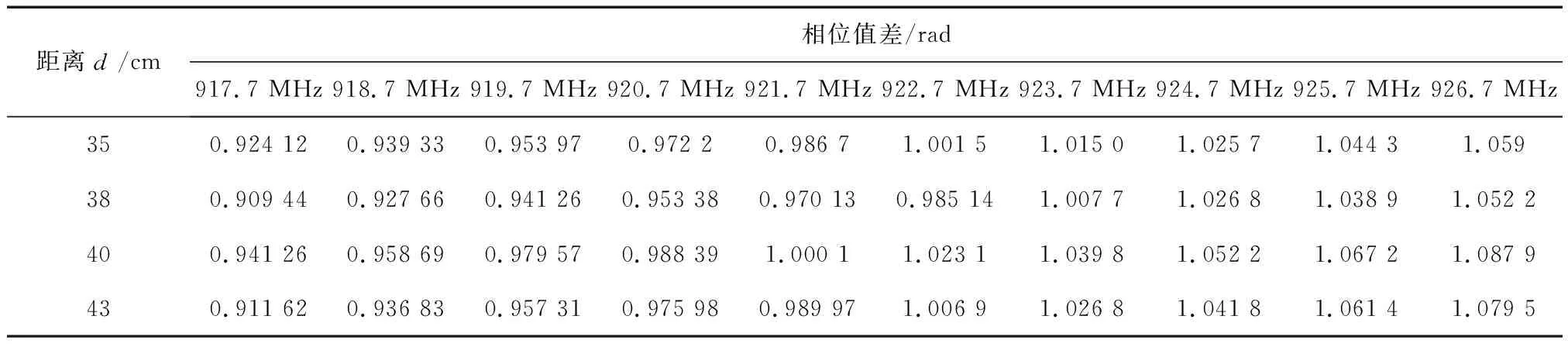
表2 超过1个波长时,频率在不同距离d下测量得到的相位差值
根据表2给出的不同距离d下各频率的测量相位差值,计算出不同频率在该距离下的测量误差,结果如图8所示。

图8 频率在不同距离下测距误差
从图8可以看出:超过1个波长,且波长整数未知时,运用多频率相位差也可以测量出标签距离,且距离越短,测量精度越高;在918~924 MHz这段频率范围内的精度较高,误差在10%之内;当频率小于918 MHz或高于924 MHz时,信号偏离谐振点较远,标签内部谐振参数对阅读器与标签之间数据传输产生的相位差影响将增大,同时距离越远,数据在传输过程中受到外界的干扰将越大,对测距精度的影响也会越大。
3 结束语
通过前面的理论分析和后面的实验验证可以看出,采用相位差测量标签距离,基本克服了标签内部电路对测距的影响,且在超过1个波长,无法确定波长整数的前提下,也能够测量出阅读器到标签之间的距离。实验结果还表明:1个波长内的测量误差在6%之内;超过1个波长时,距离越短,测量精度越高,且在918~924MHz这段频率内的精度较高,误差在10%之内。本文给出了一种对标签识别距离分析的新思路。该方法操作方便,对RFID系统中标签测距的进一步开发和研究有一定的参考价值。
[1]林亚忠,万任华,林村河,等. 一种应用于军事物流领域的无源RFIDA标签的身份认证方法[J].医疗卫生装备,2012,33(2):33-34.
[2]殷少飞,熊立志. UHF频段无源RFID标签阅读距离影响因素分析[J].现代电子技术,2008(1):38-40.
[3] Finkenzeller K.射频识别技术 [M]. 吴晓峰,陈大才,译.北京:电子工业出版社,2006:37-42.
[4]周珏书,何怡刚. 基于RCS 的无源超高频RFID 标签识别距离研究[J].计算机应用研究,2010,27(12):4594-4596.
[5]谢晶晶,赵东东. UHF Passive RFID标签最大阅读距离的研究[J].电子测量技术,2012,35(3):699-792.
[6]陈敏,杜小平. 一种提高相位激光测距精度的方法[J].现代电子技术,2005(16):113-114.
[7]王颖.基于等效频率的相位噪声测量系统的研究[D].西安:西安电子科技大学, 2009.
[8] EPCglobal Generation 2 RFID[EB/OL]. (2006-12-20).[2013-04- 05].http://www.Impinj.oom/Monza.
[9]廖惜春.高频电子线路[M].北京:电子工业出版社,2010:12-16.

