新疆于田 MS7.3地震主震精定位研究

王俊 宋秀青 陈向军 詹小艳 缪发军刘双庆 朱元清

1)江苏省地震局，南京市玄武区卫岗3号 210014

2)上海市地震局，上海 200062

3)新疆维吾尔自治区地震局，乌鲁木齐 830011

4)天津市地震局，天津 300201

0 引言

据中国地震台网中心测定，2014年2月12日17时19分在新疆于田发生MS7.3地震，此次地震的震中位于36.1°N、82.5°E，震源深度12km。截至17日08时00分，共记录到余震3294次，其中5.0～5.9级地震1次、4.0～4.9级地震16次、3.0～3.9级地震40次。据新疆维吾尔自治区地震局的调查结果，新疆于田MS7.3地震震中区的烈度为Ⅸ度，Ⅷ度区及Ⅸ度区分布在高山无人区。等震线长轴呈北东东向分布，灾区总面积约128310km2，地震造成的直接经济损失为10.8亿元，属于较大的破坏性地震(http://www.eq-xj.gov.cn/)。此次地震震中位于青藏高原西北缘，塔里木盆地的南缘，震源区附近的地质结构复杂，是西昆仑地震带康西瓦断裂、阿尔金地震带和东昆仑地震带可可西里断裂的交汇区域，距2008年3月21日发生的MS7.3地震仅约100km(图1)。

图1 精定位时所选用的地震台站和台阵(左下角)分布

于田MS7.3地震发生后，国内外多个机构都给出了主震震源位置的测定结果。中国地震台网中心、美国地质调查局(USGS)、德国 GEOFON数据中心以及美国哥伦比亚大学Global CMT工作组等给出的详细结果见表1。图2为各个机构测定结果的分布图。由图2可见，各机构给出的测定结果有较为明显的差异，震中分别分布在阿尔金断裂带的不同分支附近。因此，精确可靠的震源位置不仅可以为发震断层的判定提供依据，还是研究震源区孕震环境、深部构造以及地球内部物理学的重要基础数据(朱元清等，1997;张国民等，2002;寿海涛等，2007;万永革等，2010)。此外，还可为运用相对定位法(如双差定位法)对后续余震序列的精定位提供准确的初始参考位置(Waldhauser et al，2000;Shutianet al，2011)。

表1 世界主要机构及本文测定的主震震源位置

图2 各机构及本文测定的震中位置和附近的断层分布

为获得此次地震的准确位置，本文首先采用单纯形法对于田地震主震的震中进行初始定位，然后再根据和田台阵记录波形计算出的方位角进行校正。新疆数字地震台网和新疆和田台阵都清晰、完整地记录到此次地震的全过程，这为本文采用区域地震台网和台阵联合定位的方法精确测定此次地震的震中提供了方便。

1 主震的初始定位

1.1 单纯形法

单纯形法是一种直接搜索法，与网格搜索法的区别在于它们的搜索规则不同，属于非线性最优化理论中的全局搜索算法。单纯形法是通过在模型空间中构造单纯形来逼近目标函数的极小点，它不需要求偏导数或逆矩阵(Prugger et al，1988;朱元清等，2002)。每构造 1个单纯形，就计算其各顶点的目标函数值，并确定其目标函数的最大点、最小点，然后通过扩展、压缩、反射等算法来构造新的单纯形，以使目标函数的极小点能包含在单纯形内。单纯形是1个几何形体，其顶点个数比要确定的参数个数多1个。例如，二维空间中的单纯形是1个三角形，在三维空间中的单纯形则是1个四面体。由于它是求目标函数的极小值，因此当初值合适或地震台站分布包围震中时能避免解陷入局部极小值。该方法是目前最常用的定位方法，也是数字地震台网定位系统(JOPENS/MSDP)中的首选定位方法①赵仲和，2010，区域地震台网的地震定位，见:全国地震台网实用技术培训之统一编目培训班讲义。

1.2 定位台站的选取

震源的精确定位依赖于诸多因素，如地震台网布设的合理性、所读取的到时资料的质量以及所采用的地壳速度结构模型等(周仕勇等，1999)。张天中等(2007)认为，近台和远台资料的联合使用，有利于得到较为精确的定位结果。为了获得可靠的初始定位结果，本文从新疆、西藏、青海地震台网中选取了26个基本等方位角均匀分布的台站(平均间隔约为15°)进行地震精定位，选取的记录台站中还包含有一定比例的远台(震中距大于800km的有4个)，最后筛选出的台站的震中距范围在50～1100km(图1)。朱元清等(1997)认为提高震相到时的读取精度是提高定位精度的重要措施之一，本文在重新拾取初至震相到时的过程中，将数字波形放大至初至前的地脉动清晰可见，量取的初至误差小于0.05s。此外，由于近台S-P可以很好地控制震中距，故特别将距离震中最近的于田地震台(代码YUT)记录的波形旋转至径向和切向上以精确读取Sg波到时，旋转后T、R、Z分向的波形如图3所示，最后测得的Sg-Pg到时差约为6.5s。

图3 于田台旋转至切向 (T)、径向(R)和垂直向(Z)的波形

1.3 “3400走时表”修正

新疆地震台网长期以来一直使用“3400走时表”进行地震定位，所以本文先采用该走时表来对主震震中进行定位，结果为36.25°N、82.67°E，总的走时残差为0.935s。

“3400走时表”是根据新疆地区的平均速度模型建立的，与震源区速度模型之间存在一定差异，特别是于田地震处于构造带边缘的交汇区，结构相对复杂，因此本文对震源区周围的速度模型作了进一步修正。具体做法是:以震中为圆心、半径为1°范围内的历史地震数据为基础(包含此次地震的观测数据)，采用滑动窗线性拟合求得的波速来修正“3400走时表”。最后拟合求得的Pg、Pn波的 速度分别为5.960、8.215km/s(陈向军等，2014)，修正后的“3400走时表”结果如图4所示。再次定位获得的震中位置为36.22°N、82.52°E，发震时刻为2014年2月12日17时19分48.2秒，总的走时残差为0.547s。

对比修正前、后总的走时残差，可以清楚地看到相对于“3400走时表”的平均计算结果，修正后的走时残差显著减小。单纯形法中残差反映的是在反演过程中构造新的单纯形的收敛状况，是收缩、扩展、紧缩系数的综合体现，其值越小代表越收敛。图5为台站的走时残差分布。由图5可见，修正后的正态分布形式要明显优于“3400走时表”的平均计算结果。表明采用修正后的走时结构进行地震震中定位，理论上可以证明其结果应该更趋于目标极值。

图4 “3400走时表”修正前、后对比

图5 “3400走时表”修正前、后的定位走时残差分布

2 台阵方位角校正

地震台阵与区域地震台网的主要区别在于数据分析时采用的技术不同，地震台阵可以通过不同传感器之间的信号延时来获得精确的台阵-事件方位角(反方位角)估计(赵镇岭等，2002;寿海涛等，2007;Borrman，2012)。此次于田地震除了固定的区域数字地震台站记录以外，新疆和田台阵的10个子台(其中 1个为宽频带台站，9个为短周期台站)也清晰、完整地记录到此次地震的全过程，震中距台阵中心约320km，波形记录的信噪比非常高(图6)。这为本文采用地震台阵的记录波形来精确校正地震的方位角提供了很好条件。和田地震台阵采用中心子台和2个同心圆结构布局，内环半径约为600m，外环半径约为 1500 m。据段天山等(2009)的分析结果，和田台阵所记录的 P波信号具有非常好的相关性，在1～4 Hz的频率范围内，无论是远震、区域震还是近震信号，在3000m的子台间距范围内，信号相关系数都可以保持在大于0.8的水平，并且没有呈现出信号相关系数随子台间距增大而明显下降的趋势。台阵中心位置与此次地震震中的分布如图1所示，各子台的分布如图1中左下角方框所示。当震源距远大于10倍波长时，传播到台阵的地震波可近似为平面波(Almendros et al，1999)，在假定的圆形波阵面情况下，震中方位角和波阵面的传播方向在水平面上的投影可以用角度φ和θ表示(图7)。

图6 和田台阵的记录波形

图7 台阵参数示意图

和田台阵中各站点之间的相对高程差均小于 50m(唐明帅等，2010)。因此，本文中不考虑子台间高程差异，即忽略高程对到时的影响。那么，位于同一水平面上子台间的到时差与相对距离之间的关系可用下式表示(Borrman，2012)

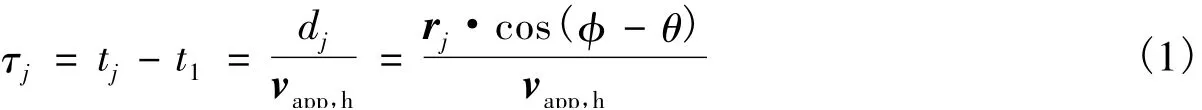
式中，rj为仪器j的位置矢量，指距指定参考点的距离(绝对值);Φ为反方位角(通常简写为BAZ)，等于波阵面路径的角度，即台站对震中的方位角;θ为台站和参考点连线与正北方向的夹角，从正北开始起算;vapp，h为视速度矢量，本文中对确定的震中位置可以用 Pn的速度来代替。理论上，dj/vapp，h与τi之差应等于零。但在实际观测结果中，由于假定的速度模型与真实地球模型之间存在差异以及波阵面并非是完全平面，因此，它们之间的差并不等于零。于是，本文联合和田台阵中所有子台来定义如下形式的目标函数，即

式中，n为子台总数，通过在0°≤Φ＜360°的范围内搜索目标函数ε的极值，极值对应的角度即为台阵对震中的方位角。

为精确量取各子台间的相对到时，本文在初至波到时后15s的时窗内，搜索记录波形中起伏最为尖锐部分到达的时间，如图6中黑色箭头所示。需要特别指出的是，通过台阵的波形聚束也可以得到同样的结果。

根据上述方法，在整个空间内搜索出的目标函数值结果如图8所示。图8中黑色箭头所对应的极值即为所求的方位角，约为110.9°。而由单纯形法定位结果所获得的方位角约为110.0°，两者相差0.9°。于是根据方位角误差和震中距，依据下式，便可计算出在320km处的位置修正值约为5.1km。

图8 目标函数随角度的分布

最后，以初始定位的位置为起点将位置修正值5.1km，沿经、纬度分解后进行震中位置修正，最终获得震中位置为:36.197°N、82.467°E(图 2)。

3 讨论与结论

本文通过区域地震台网和地震台阵的联合定位方法，最终精确测定出新疆于田MS7.3地震的震中为 36.197°N、82.467°E，震源深度 12km，发震时刻(北京时间)2014年 2月 12日17:19:48.2。震中误差±3km。需要说明的是，主震的震源深度是采用朱元清等(1990、1995、1997)提出的确定性方法所测定的结果，深度误差为±2km(宋秀青等，2014)。

本文对新疆于田MS7.3主震定位采用的方法如下:①对新疆当地的“3400走时表”进行校正，采用了符合本区域的地壳速度模型;②利用于田地震台记录的波形旋转至径向和切向上来精确测定 S波到时，并以此控制震中距离;③利用台网资料采用环绕震中等角度选台的方法进行定位，实践和理论都证明如此处理的结果对复杂地区的地震定位效果更好;④应用了和田台阵的资料，用台阵对震中进行了方位角校正。综上所述可见，本文充分地利用了台网和台阵的资料，并结合当地地壳速度结构，尽可能采取合理的方法进行了综合处理。因此，理论上是可以提高定位精度的。

合理地给出定位误差在精定位工作中十分重要。本文在采用单纯形法进行地震定位后，为了检测该结果，采用抛台试错方法来检验结果的稳定性。具体做法是将所有定位台站循环、逐个(每 次只抛弃1个台站)抛弃后再定位，最后获得25次定位结果的走时残差基本稳定在0.60s左右，震中位置基本不变。结果表明，采用该方法进行地震定位时获得的结果是稳定的，所选取的台站在各个方位上的权重比例基本相当。

此外，本研究在定位时采用震源区附近的历史数据修正“3400走时表”，这可使由速度模型引起的系统性定位偏差显著减小(图4)。

和田地震台阵中各子台的相对到时，是以搜索初至时间段内能量最强的同相波形极值所到达的时间来表示，或者也可以通过台阵的波形聚束来求取，而非直接量取首波Pn的到时。这是由于首波的能量相对较弱，在记录图上的信噪比相对较低，直接读取 Pn到时的误差也会加大。依据式(2)可知，由地震台阵波形记录到时相对误差所引起的最大方位角误差约为0.3°，方位校正引起的震中位置误差约为1.5km。

需要说明的是，由于采用单纯形法定位，因此不能直接采用误差椭圆的形式对定位误差进行描述。但可以采用数值检验，即假定结果偏离震中位置，以一定的步长计算偏离震中位置时的误差分布来定量描述计算结果的误差范围。本文以最终的震中位置为中心，在约100km2范围内，计算了以1km为步长的网格节点处的理论走时与实际观测走时差的均方差分布(图9)。从图9中可以得到以下结论:①经校正后的震中位置的走时残差为0.32s，较初定位时的走时残差0.547s更小;②震中位于离理论均方差最小极值中心位置约1km处，加上方位校正引起的震中位置误差约1.5km，故可以估计震中位置的理论误差约±3km。

图9 理论走时与实际观测走时差的均方差分布

致谢：感谢中国地震局地震预测研究所赵翠萍研究员、新疆数字地震台网冉慧敏以及江苏省地震局李迎春博士、李峰博士提供GMT绘图所需的断层数据。感谢中国地震局监测预报司、中国地震台网中心、江苏省地震局、上海市地震局、新疆维吾尔自治区地震局、天津市地震局和地震震源深度研究推进小组全体成员对本文研究工作的大力支持和帮助。