新疆全区和分区地壳速度模型的分析

陈向军 上官文明 宋秀青 王俊 刘双庆缪发军 朱元清

1)新疆维吾尔自治区地震局，乌鲁木齐市新市区科学二街338号 830011

2)上海市地震局，上海 200062

3)江苏省地震局，南京 210014

4)天津市地震局，天津 300201

0 引言

如何得到合适的地壳速度模型是地震学研究中的经典问题。准确地测定地震震中的经纬度和震源深度一直是地震学家关心和研究的热点(朱元清等，1997b)，而地壳速度模型与地震的定位精度密切相关①赵仲和，2010，区域地震台网的地震定位，见:全国地震台网实用技术培训之统一编目培训班讲义。同样，在测定地震震源深度时，地壳速度模型的作用更加突出(朱元清等，1990)。在日常地震监测工作中，合适的地壳速度模型可以帮助地震学家准确地判断测定的精度(朱元清等，1997b;张天中等，2007)。全球性的分层速度模型有IASPEI91、AK135等，但是这些模型不能够满足区域尺度的地震定位(李志伟等，2006)。新疆占中国国土面积的1/6，天山山脉横贯东西，南边紧靠帕米尔高原，又夹于塔里木盆地和准噶尔盆地之间，东西绵延约2500km，其具有的特殊地质构造活动背景被认为是印度板块与欧亚板块碰撞的结果(孙安辉等，2011;Abdrakhmatov et al，1996)。新疆复杂的地质构造使得当对该地区发生的地震进行精定位时，选用适合震区的速度结构模型就显得十分重要(唐明帅等，2010)。

新疆全区大震频繁，地震丛集，随着地震台网监测能力的提高，每年记录到的发生在本区的地震数已经超过2万个，其中有多台记录的地震比例超过50%。这对研究新疆地区的速度结构提供了极大的帮助。根据历史上新疆全区记录的地震震中分布图，可以清楚地划分出3个地震密集区域，即中天山地区、喀什地区和于田地区。

本文对全新疆范围的平均速度模型、3个地震密集区域的区域速度模型以及“3400走时表”进行了分析研究，特别是对2014年2月12日新疆于田MS7.3地震及其附近区域进行了地壳速度结构的拟合，得到了符合地震实际记录结果的速度结构模型。此外，多年丰富的地震震相数据使我们能对得到的速度结构模型的可靠性和稳定性进行分析，这对认识新疆地区各分区地壳速度模型的差异十分重要。

1 “3400走时表”的地壳速度模型解析

前苏联 И.Л.涅尔赛索夫、Т.Г.拉乌金1964年发表了“3400km走时表”(以下简称“3400走时表”)，其测线从帕米尔至贝加尔，全长3500km，穿过中亚、哈萨克斯坦、阿勒泰萨彦和贝加尔湖沿岸等几个地区。新疆与其中的中亚、俄罗斯西萨彦岭相邻，“3400走时表”的西部走时表也部分适用于新疆地区，该成果在新颖性、严谨性等方面胜过在新疆应用的其他走时表。新疆有帕米尔地区的中深源地震带，也有阿勒泰运动学及动力学明显异常的地区，即使沿天山两麓的地震带，也有西克尔、呼图壁等范围较小的走时异常区(新疆地震局分析预报室，1982;张诚等，1977;曾融生等，1965)。

“3400走时表”是一个大范围内的平均走时表，震中距愈大，符合愈好。在小区域范围内，其结果偏差稍大。“3400走时表”在震中距0～50km时由于受震源深度及小构造的影响，时距曲线的双曲线弯曲程度不同而未给出数据。这段空白是根据新疆新源大爆破得到的地壳参数、速度值进行计算填补上的，其在Δ(D)=50km处衔接较好②新疆地震局办公室，1982，3400公里内的地震波走时表手册。

由于历史上新疆地震观测台站较少，故从1977年“3400走时表”在新疆推广使用以来，其运动学特征在新疆较大范围内基本符合。2000年以来“3400走时表”依然作为重要的走时表在继续使用。但其蕴含的地壳速度模型一直不清晰，相关研究较少。为了更好地研究如何以地震密集区域建立分区地壳速度模型，首先需要解析“3400走时表”的速度模型。

1.1 “3400走时表”分层速度的解析

“3400走时表”直接给出了震中距和3种主要地震波的走时，故可以采用时距曲线拟合的方法直接计算Pg、Pb、Pn速度。其中Pg、Pb和 Pn分别代表直达P波、康拉德面和莫霍面的滑行波。计算结果表明“3400走时表”为2层均匀模型，第1层速度为5.960km/s，第2层为6.302km/s，莫霍面速度为8.364km/s(图1)。

1.2 “3400走时表”固定震源深度的解析

根据“3400走时表”Pg到时数据，震中距为0时走时为1.7s，依据vPg=5.960km/s，可计算得到“3400走时表”暗含的震源深度为:H=1.7s×5.960km/s≈10km。因此，“3400走时表”为固定震源深度为10km的走时表。

图1 新疆“3400走时表”时距曲线

1.3 “3400走时表”2层速度模型层厚的解析

以震源深度为10km分析“3400走时表”，Pn、Pb首次分别出现在震中距200、250km时。根据地震学的时距理论关系，在已知vPg、vPb、vPn和对应的走时条件下，可以计算出对应“3400走时表”的2层模型平均厚度，其深度应该分别对应于康拉德面和莫霍面的平均深度。

(1)康拉德面深度计算

已知:H=10km，Δ(D)=250km(Pb)，vPg=5.960km/s，vPb=6.302km/s，变换H+h(变量)，依据斯奈尔定律和走时方程，分别计算对应不同震中距的Pb走时。根据经验可以假设第1层的厚度小于60km，即h∈［1，50］。计算表明，当h=12km、H+h=22km时，不同震中距的理论Pb走时与“3400走时表”的所有对应震中距的走时数据一致，从而得出第1层的厚度为22km，即康拉德面深度为22km。

(2)莫霍面深度计算

已知:H=10km，Δ(D)=200km(Pn)，vPg=5.960km/s，vPn=6.302km/s，第1层的厚度为22km，变换H+h+L(变量)，依据斯奈尔定律和走时方程，分别计算对应不同震中距的Pn走时。根据经验可以假设第2层的厚度小于100km，L∈［1，80］，当H+h+L=57km，即L=35时，不同震中距的理论Pn走时与“3400走时表”的所有对应震中距的走时数据一致，从而求得第2层的厚度为35km，即莫霍面深度为57km。该结果也与前人采用不同方法得到的结果基本一致(刘文学等，2011)。

1.4 “3400走时表”速度模型的误差分析

综合上述结果可以得到“3400走时表”地壳速度模型如表1所示，其中康拉德面深度为22km，莫霍面深度为57km。对该结果的验证如下:已知震源深度H固定为10km，vPg=5.960km/s，v康拉德面=6.302km/s，v莫霍面=8.364km/s。根据“3400走时表”中给出vPg、vPb、vPn的起始、终止距离，变换震中距 Δ(Pg)∈［0km，850km］，Δ(Pn)∈［250km，1200km］，根据地震波射线路径计算Pg和Pn走时表。结果显示，Pg理论走时与“3400走时表”Pg走时总体的标准差为0.099s，误差小于0.2s的占到走时表全部路径中0～850km的93%;Pn理论走时与“3400走时表”Pn走时的标准差为0.055s，误差小于0.1s的占到走时表中全部路径中250～1200km的 97%。说明该速度结构模型可以较好地表示“3400走时表”。

表1 “3400走时表”速度模型

2 新疆全区和分区地壳速度结构分析

自2008年“十五数字地震观测网络项目”实施以来，新疆地震记录的数据量一直处于全国前列，每年多达2万条以上，至2014年已经积累了丰富的测震震相数据资料。根据新疆地震震中分布图很容易区分出新疆的3个地震密集区域，即中天山地区、喀什地区和于田地区。这3个地区多台记录的地震事件数量占新疆全部地震事件的76%，其中中天山地区占48%，喀什地区占27%，于田地区占1%，这些区域均为M≥3.0地震的多发区(表2、图2)。该现象与新疆测震台站的空间分布及新疆特殊的地质构造相符。

表2 新疆2009年1月～2013年12月有多台记录到的地震事件分区表

图2 新疆地震震中分布

2.1 新疆全区地壳速度结构分析

地壳速度结构的数值模拟和分析方法已经非常成熟，本文的研究重点在于如何分析处理新疆数字地震台网记录到的几十万条震相数据，以得到能较好反映新疆地区特征的地壳速度。根据中国地震局地震编目标准化的要求，自2008年7月份开始，全国将所有地震震相编目数据录入了中国地震台网中心的地震目录数据库。本文所使用的震相数据均来自该数据库。

拟合方法的基本思路为:根据新疆数字地震台网各个台站实际记录到的走时和震中距资料，采用线性拟合和滑动窗拟合两种方法进行。在拟合前先对数据进行必要的预处理，滑动窗是在全部资料包含的震中距范围内，以150km为固定窗长，并按50km的间隔进行滑动线性拟合(图3)，最后根据每个窗所获得的结果进行加权平均求出最后的速度结果。在滑动窗拟合的过程中，如果单个窗内样本数少于平均样本数的80%，则不参加最后的加权平均计算。

图3 滑动拟合的示意图

加权平均的具体做法是:首先，计算所有单个窗内获得结果的总平均值;然后，将每个窗内的结果与平均值之比的倒数作为权重系数，并将权重系数乘以相应窗对应的值后再求平均。其物理意义表示偏离平均值越远的值，其权重系数就越小。

本文线性拟合是求2个变量X、Y之间的线性函数关系

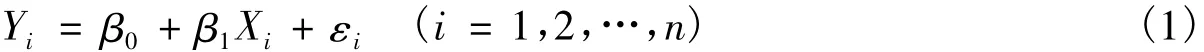
其中，(Xi，Yi)表示(X，Y)的第i个观测值;β0、β1为参数，β0+ β1Xi为反映统计关系直线的分量;εi为反映在统计关系直线周围散布的随机分量，εi～N(0，σ2)，εi服从正态分布。式(1)中 β0、β1均为未知数，根据样本数据对 β0和β1进行统计，β0和 β1的统计值为b0和b1，建立一元线性方程

利用最小二乘法，可求得b0和b1使每个样本观测点与拟合线性方程之间的偏差最小。

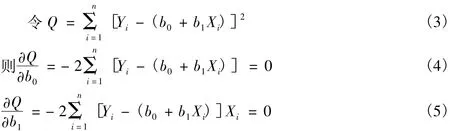
在中国地震台网中心的地震目录数据库里，对82个地震台站记录到的2009年1月1日～2013年12月31日地震事件的所有震相数据进行预处理，得到可用的Pg震相数据201326条、Pn震相数据73589条。Pg震相数据直接拟合求得的速度为6.22km/s，均方差为1.22s;Pn震相数据直接拟合求得的速度为为8.47km/s，均方差为1.87s。滑动窗方法的拟合可以进一步研究新疆地壳结构分段速度的稳定性。Pg震相数据滑动加权平均拟合的速度为6.18km/s，Pn震相数据为8.37km/s。

为避免震源深度对速度拟合的干扰，又选择震级大于2.0级，震中距在50～250km范围的Pg震相数据进行速度拟合，计算得到的速度vPg=6.19km/s;选择震中距在250～700km范围的Pn震相数据进行速度拟合，计算得到的速度vPn=8.34km/s。之所以选择Pg震相数据的震中距在50～250km，除了考虑避免震源深度对速度拟合的干扰外，还考虑到当震中距小于250km时，Pg震相数据的到时在新疆地区大多为初至，容易正确辨认。选择Pn震相数据的震中距在250～700km，主要原因是当Pn震相在震中距大于250km以后为初至，也容易正确辨认。取700km的距离主要是考虑除了中强地震，绝大多数地震的记录其震中距小于700km。如此得到的分析结果能较好地代表新疆全区的平均速度，且便于对比和评价。

计算结果表明，新疆全区3种方法拟合得到的vPg=6.18～6.22km/s，平均6.2 km/s。vPn=8.34～8.47km/s，平均8.4km/s。对比近4年由新疆天然地震数据拟合的速度结果与由“3400走时表”速度模型拟合的结果，发现2个比较突出的特征。一是新疆全区天然地震Pg、Pn震相数据拟合的速度结果的均方差分别为1.22、1.87s，表明全区的vPg、vPn均比较离散;二是天然地震vPg比“3400走时表”速度模型的结果系统地偏大4%，而vPn与“3400走时表”速度模型所得结果基本一致，仅偏大0.4%。

近年来，中国地震局要求日常编目工作的震相标注必须严格以波形特征读图标注震相。而由上述vPg、vPn的离散宽度和vPg的系统偏差结果可见，新疆全区的波速存在较大的区域性差异，所以研究各个地震密集区的地壳速度结构可以更好地满足地震监测的需要。

需要指出的是，“3400走时表”速度结构模型给出的康拉德面和莫霍面的平均深度还是可以作为新疆地壳速度结构的重要依据的。

2.2 中天山地区地壳速度结构分析

对中天山地区2009年1月～2013年12月的地震震相数据预处理后，再分别对所有Pg、Pn震相数据进行总体拟合、滑动窗分段拟合以及滑动加权平均的计算。另外考虑到中天山地区的空间特点和丰富的震相数据量(达到总数据量的48%)(图2)，还对该区的vPg震相数据进行了细处理，即将该区再分为3个1°左右、地震更为密集的小区域，Pg震相震中距取值50～250km。结果显示，vPg值在该区域从西向东逐渐减小，从6.16 km/s减小到6.02km/s，且标准差较小;Pn震相震中距取值范围250～700km，vPn数值的稳定性较好，具有区域代表性。震相取值范围即选择震中距的理由与前述新疆全区地壳速度结构分析中的依据一致。与“3400走时表”速度结构模型相比，vPg在该区域处于相对高值，区域差异明显;vPn相对较稳定，差值较小。

通过对比分析各项拟合结果(表3)，本文中vPg取平均值6.14km/s，vPn取平均值8.33km/s。当然也可以取其他数值，但是差别不大，这一点可以进一步通过地震精定位的方式来确认。

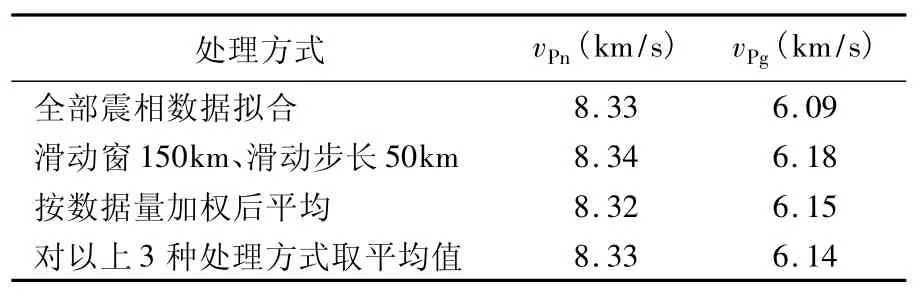
表3 中天山地区3种方法求得的vPg、vPn速度

2.3 喀什地区地壳速度结构分析

喀什地区处于天山山脉与昆仑山脉交汇区，断层发育，地质构造破碎。为了与中天山地区进行对比，选择了同时段数据，采用了3种相同的Pg、Pn速度计算方法。Pg震相震中距取值50～250km，Pn震相震中距取值250～700km。结果表明，vPg、vPn值与中天山地区差异不大，但是从全部震相数据拟合的速度对比来看，喀什地区的vPg平均值为6.14km/s，比中天山地区(vPg=6.09km/s)略大，这进一步表明了新疆各区域的地壳速度差异和西部的vPg略大于东部;vPn值在震中距大于500km后趋于稳定，略大于“3400走时表”模型中天山地区的vPn。从新疆全区范围来看，vPn值的波动较小，数值较稳定。

经过对各项拟合结果的对比分析(表 4)，vPg取均值 6.13km/s，vPn取均值8.39km/s。

同样也可以取其中间值，这也可以进一步通过地震精定位的方式来确认。

表4 喀什地区3种方法求得的vPg、vPn速度

2.4 于田地区地壳速度结构的分析

2014年2月12日新疆于田发生了MS7.3地震，所以本文特别讨论了于田震区的地壳速度模型，以便用于主震的精定位和地震序列的深度测定。

由于于田地区的地震密集区域范围和前2个区域相比较小，震相数据明显较少，所以为确定于田震区地壳速度采用了如下4个参考模型:①前述的“新疆3400走时表”速度模型;②选用以2014年于田MS7.3主震为中心，半径为1°范围内，自2009年1月以来M≥2.0所有地震事件的Pg、Pn震相数据，该范围包含了2008年该区域的另一个7.3级地震，通过时距曲线拟合方法，计算其速度值，考虑到该区域数据量较少而没有采用滑动窗方式;③采用2014年2月11日于田5.4级、2月12日于田7.3级、2月12日于田5.7级地震事件的Pg、Pn震相数据，通过时距曲线拟合方法，计算其速度值;④仅采用2014年2月12日于田7.3级主震事件的Pn震相数据，通过时距曲线拟合方法，计算其速度值。

由4个模型计算出的结果如下:模型①vPg=5.96km/s，vPn=8.364km/s;模型②vPg=6.07km/s，vPn=8.298km/s;模型③vPg=5.98km/s，vPn=8.239km/s，其拟合效果见图 4(a);模型④计算时考虑到于田MS7.3主震震相数据中Pg震相过少，故仅对Pn震相数据进行了拟合，计算得到vPn=8.21km/s，其拟合效果见图4(b)。

需要强调的是，用上述4种参考模型来确定新疆于田7.3级地震主震区地壳速度模型是基于从整体到局域来观察和分析该区域速度结构的思路。由上述4种方法得到的vPg=5.96 ～6.07km/s，均值为 6.00km/s;vPn=8.21 ～8.364km/s，均值为 8.277km/s。由此可知，该地区的vPg均值相对比较稳定，然而于田7.3级主震震中附近的近台较少，绝大多数为远台，所以使用合适的vPn将对定位结果有较大的帮助。

图4 2014年于田MS7.3地震前震及M≥5.0主、余震震相数据拟合计算vPg、vPn

为确定4种模型计算结果的合适初始速度，特作如下假定:①如果由多种方法求得的结果和现在一直使用的结果一致或差别很小则选用原结果，反之则用新的计算结果;②如果没有更好的方法、资料和结果证明原常用结果的不正确则选用原结果，反之则用新的计算结果;③通过试错法来计算震区主要地震的震中位置和震源深度，根据定位误差和震源深度的收敛程度判定模型分层速度和厚度。

试错时初始模型以新疆“3400走时表”速度模型为原型，结合4种分析结果分别调整该速度结构的不同参数，通过单纯形法试错震中位置，通过PTD方法(朱元清等，1990、1995、1997a)试错震源深度，然后综合统计分析试错的结果，深度收敛，定位误差小的速度结构模型选为最终结果。最后得到适合新疆于田MS7.3地震序列的地壳速度模型:第1层速度为5.96km/s，厚度22km;第2层速度为6.302km/s，厚度为35km;莫霍面速度为8.21km/s，深度为57km。

用PTD方法来计算震源深度时，地壳深度结构模型中的各层层厚对深度的影响很大，不适合的地壳厚度将会使深度的结果发散(宋秀青等，2014)。单纯形法是一种直接搜索法，是非线性最优化理论中的全局搜索算法。单纯形法通过在模型空间中构造单纯形来逼近目标函数的极小点，它不需要求偏导数或逆矩阵(Prugger et al，1988;朱元清等，2002)。当地震台站包围震中时用单纯形法可以有效地确定震中位置，这时地壳速度结构模型的优劣会直接在走时误差中反映出来(王俊等，2014)。

3 讨论与结论

通过分析“3400走时表”的地壳速度模型和处理新疆27万余条地震震相数据，分别对新疆全区以及中天山地区、喀什地区、于田地区等3个地震密集区的地震震相资料进行了分析研究，得到以下结论:

(1)“3400走时表”作为一个大区域的平均走时表，其速度模型为固定震源深度为10km的2层模型，即第1层速度为5.96km/s，厚度22km;第2层速度为6.302km/s，厚度35km;莫霍面速度为8.364km/s，深度57km。

(2)新疆3个地震密集区的区域地壳速度存在明显差异。其各自的平均速度模型结果:中天山地区vPg=6.14km/s，vPn=8.33km/s;喀什地区vPg=6.13km/s，vPn=8.39km/s;于田地区vPg=6.00km/s，vPn=8.277km/s。(3)适合2014年于田MS7.3地震序列使用的地壳速度模型为2层，vPg(第1层速度)为5.96km/s，第2层速度为6.302km/s，深度22km;vPn(莫霍面速度)为8.21km/s，莫霍面深度为57km。

需要特别指出的是，本研究工作的目的是讨论如何在复杂的地质构造区，根据巨量的地震震相资料，获得能供地震台网日常分析地震事件使用的等效的平均速度结构。

综合上述分析结果，建议新疆数字地震台网日常分析地震事件时采用地震密集区速度结构模型，而对于大震序列的精定位则应采用地震序列区域的局域地壳速度模型以提高地震定位的精度。

致谢：感谢中国地震局监测预报司、中国地震台网中心、新疆维吾尔自治区地震局、上海市地震局、江苏省地震局、天津市地震局和地震震源深度研究推进小组全体成员对本文研究工作的大力支持和帮助。