预应力混凝土结构桥梁锚下控制力反算方法探讨

李海东,朱文盛,周仕军

(中铁西南科学研究院有限公司桥梁与结构工程研究所,四川成都611731)

在后张法预应力施工过程中，管道不可能与设计曲线完全吻合，预应力筋在锚固时的回缩可能偏离于设计值。若不调整张拉力，会导致结构的有效预应力不够，危及结构安全。根据实测摩阻参数计算张拉力是预应力施工的重要工作。

1 预应力结构预应力损失计算

以图1所示梁体为研究对象。有效预应力的控制断面为锚固端，钢绞线投影长度为L，偏转角度为θ，摩阻及偏差系数设计值分别为μd、kd，回缩值为ΣΔld。

图1 预应力筋布置示意

(1)管道摩阻预应力摩阻损失。只考虑管道摩阻损失时，由管道摩阻引起的应力损失为：

σl=σcond·[1-e-(μθ+kx)]

(1)

(2)钢绞线回缩预应力损失。锚固时，夹片在钢绞线的带动下进入锚孔将钢绞线夹紧锚固。假设锚具夹片自油顶放松至锚固后的行程为Δl1，如图2。锚固时，钢绞线与夹片之间存在相对滑移，且在锚固后，锚具将承受巨大的压力并使其压密变形。假设该两项之和为Δl2。此外构件接缝在锚固后将压密，假设该类变形为Δl3。该三项均使预应筋放松。回缩值之和为∑Δl=Δl1+Δl2+Δl3。

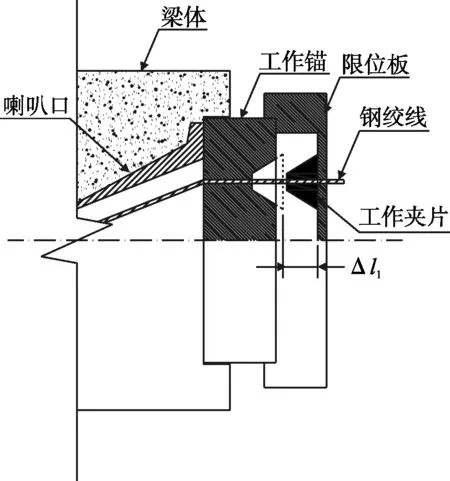
图2 预应力钢绞线锚固过程示意

在不考虑预应力筋反摩阻的情况下的预应力损失值为：

(2)

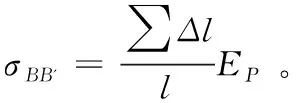
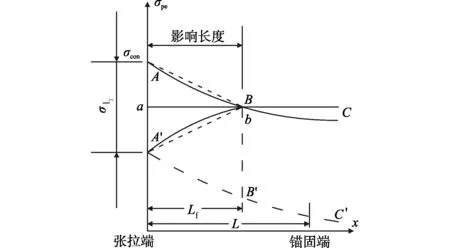
图3 考虑反摩阻及不考虑反摩阻时预应力筋应力损失计算示意

从张拉端至B点为反摩阻的影响范围区，即：

(3)

式中：σl2(x)为反摩阻影响区域范围内任意断面由于回缩导致应力的降低值。由于Ep∑Δl均为已知参数，通过试算的方法可得到影响长度。

上述计算反摩阻影响长度较复杂，可将AB、A’B简化为直线，如图3虚线。

直线AB的斜率为：

(4)

式(4)中：σx为距张拉端x处扣除管道摩阻损失后的应力；斜率Δσd即为单位长度由于管道摩阻引起的预应力损失值。

则在影响区域范围内，任意断面由于回缩导致的应力损失为：

Δσx=Δσ-2Δσdx

(5)

通过几何关系，可得张拉端由于回缩引起的预应力损失为：

Δσ=2Δσdlf

(6)

总回缩量等于影响长度范围内预应力筋应变的累计，即：

(7)

(8)

当lf≤l时，在反摩阻影响范围内，任意断面由于回缩导致的应力损失为：

(9)

2 张拉控制力的反算

假设理论设计回缩量为∑Δld，实测为∑Δlt。回缩量影响长度理论设计值为lfd，根据实测值推算的影响长度为lft。对锚固端，可能会有以四种情况：①lfd≤l，lft≤l；②lfd>l，lft≤l；③lfd>l，lft>l；④lfd≤l，lft>l。本文以情况①和情况③说明张拉控制力的反算方法。

(1)情况①：lf≤l，锚固端不受∑Δl的影响，应力损失只考虑摩阻损失。

在实际张拉时，根据控制截面有效预应力相等原则，可有：

σcont·e-(μtθ+ktl)=σcond·e-(μdθ+kdl)

(10)

实际锚下控制应力应调整为：

σcont=σcond·e[(μt-μd)θ+(kt-kd)l]

(11)

(2)情况③：lf>l，锚固端的有效预应力还受∑Δl的影响。

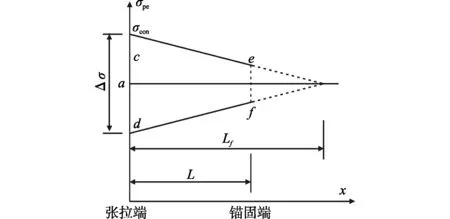
图4 lf>l时的预应力损失简化计算示意

在锚固端，由于回缩导致的预应力损失值为：

Δσef=Δσ-2·l·Δσd

(12)

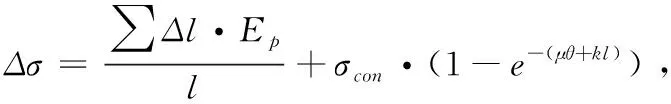
(13)

为使得锚固端的有效预应力等于设计有效预应力，锚下控制应力应调整为：

(14)

3 结束语

预应力张拉控制是预应力施工过程中一项重要的技术工作。应对μ、k、∑Δl进行测试，并根据实测值对预应力筋的张拉力进行调整。另外，在计算有效预应力时，还应考虑梁体的收缩徐变、钢绞线的弹性模量等因素。

[1] 叶见曙.结构设计原理[M].北京:人民交通出版社, 2005

[2] JTG D62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S]