浅析门架式双排抗滑桩结构参数的影响

王 丰

(重庆市市政设计研究院,重庆 400020)

1 门架式双排抗滑桩简介

门架式双排抗滑桩是从20世纪50年代开始研究的一种支挡结构。他是在滑坡地段的适当位置设置前、后两排钢筋混凝土桩，并在桩顶用刚性连梁把前、后两排桩联结起来，形成一种双排支护的空间结构，其形状与传统的门框相似，所以称为门架式双排抗滑桩[1]，结构形式如图1。

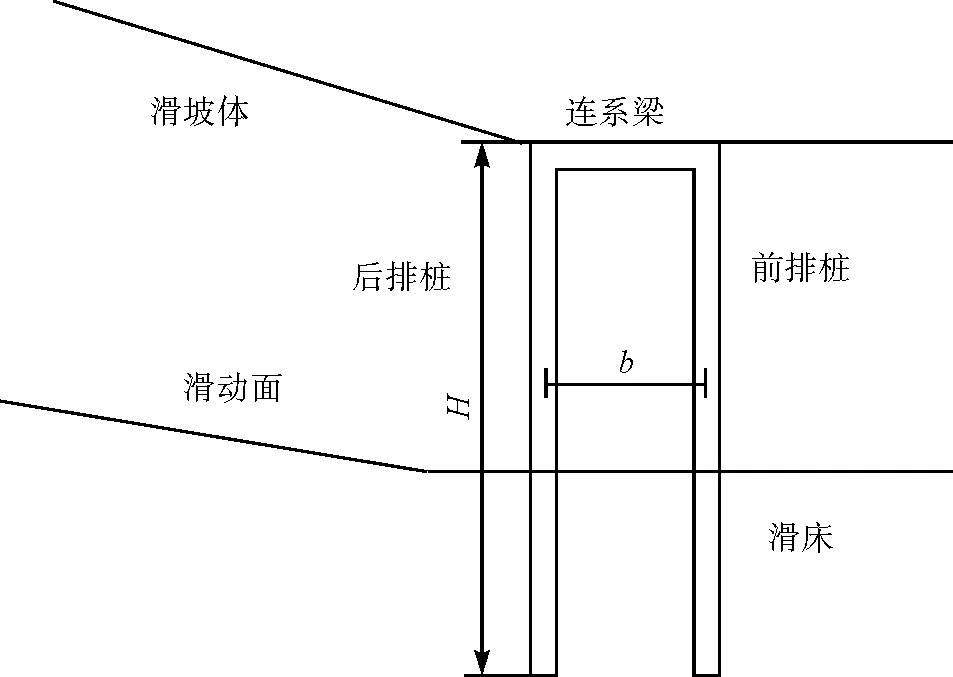
图1 门架式双排抗滑桩示意

该结构为一空间结构，可以不需要内支撑(如锚杆等)，仅靠自身的空间组合效应来抵抗滑坡推力；在滑坡推力的作用下，后排桩向滑坡前缘运动，由于结构自身的空间性，将使得桩间土体受压缩；因此后排桩就要受到桩间土体的抗力作用，而前排桩也将受到由桩间土体传递的滑坡推力作用；前排桩埋入稳定基层中，通过稳定基层提供的抗力来维持桩体的稳定。

2 计算模型

为了更好的模拟门架式双排抗滑桩的受力机理，本文在传统的平面刚架模型[2]、平面杆系模型[3]的基础上提出了一种新的计算模型，如图2所示。

图2 门架式双排抗滑桩有限元模型

该模型将前后排桩嵌入稳定基层中，利用接触单元来模拟滑动面以下桩—土之间的相互作用，利用弹簧模拟滑动面以上的土体对前后排桩的作用，利用等参四边形单元模拟稳定基层的土体，利用梁单元模拟门架式双排抗滑桩，从而分析门架式双排抗滑桩在滑坡推力作用下的变形，确定其合理的结构形式。

为了更好的模拟门架式双排抗滑桩的受力情况，针对该模型提出以下假定：

(1) 假定滑动面为平面；

(2)连梁和前后排桩刚性连结，但连梁不是绝对刚体，可以发生变形但不发生转动。

3 结构参数影响分析

根据门架式双排抗滑桩的结构特性，本文认为影响其结构受力的主要参数有排距、连梁的刚度以及桩间土的作用。本文将利用有限元模型及软件，结合工程算例对门架式双排抗滑桩的结构参数影响进行分析。

工程算例：

(1) 土的指标：滑体为碎、块石土的堆积层，自上而下变形增大，φ1=25°，γ1=21kN/m3, 滑动面以下的滑床为密实黏土层c=20kPa，φ=25°，泊松比μ=0.3，重度γ=19.0kN/m3，变形模量E=10MPa。

(2) 桩体采用C30钢筋混凝土，弹性模量E=3×104MPa，桩长22m，其中受荷段h1=12.0m，锚固段h2=10.0m，桩间距(中至中)L=6m，桩的截面尺寸b×h=2m×2.5m，梁长度可以变化。

3.1 排距对门架式双排抗滑桩的影响

排距是指前后排桩形心主轴之间的距离，合理的排距不仅关系着支挡效果，而且直接影响着工程造价。本文将利用计算模型，在保持结构其他因素不变的情况下，取排距分别为1.5d、2d、2.5d、3d、4d、5d、6d、7d、8d(d表示桩径，若桩为矩形桩则为短边长度)进行分析；通过计算，其前后排桩桩身的最大位移、弯矩如表1、表2所示。

表1 前后排桩最大位移Smax mm

表2 前后排桩最大正负弯矩Mmax kN·m

由表1可知，随着排距的增大，门架式双排抗滑桩的整体位移呈先减小后增大的趋势。当排距在1.5d～2.5d时，前后排桩的最大位移随着排距的增大而急剧减小；当排距在2.5d～5d时，前后排桩的最大位移值随着排距的增大也逐渐减小，但减小速率较慢；以前排桩为例，从表1可以看出，当排距由1.5d增大到2.5d时，桩体的最大位移由25.01mm减小为19.95mm，最大位移减小了5.06mm，减小速率为20.2%；当排距在2.5d～5d时，桩体的最大位移由19.95mm减小到19.07mm，最大位移减小了0.88mm，减小量可以忽略；当排距在5d～8d时，门架式双排抗滑桩前后排桩的最大位移又逐渐增大，但增加的趋势较缓。以前排桩为例，从表1可以看出，当排距由5d增加到8d时，前排桩的最大位移由19.07mm增加到19.72mm，增加了0.65mm。

此外，将门架式双排抗滑桩换算成等截面的普通抗滑桩，其他条件不变，得到普通抗滑桩的受力情况。当排距为1.5d时，前后排桩的最大位移基本相同，其值为25.1mm；而普通抗滑桩的最大位移为48.1mm，此时的门架式双排抗滑桩基本上就相当于将两根普通抗滑桩叠加在一起共同抵抗滑坡推力；随着排距的增大，门架式双排桩的整体位移又逐渐减小，前后排桩之间的最大位移也将有所不同，此时的门架式双排抗滑桩又不是简单的将普通抗滑桩叠加在一起；由于连梁的存在，门架式双排抗滑桩又具有了一定的空间性，结构的整体刚度增大，其结构的最大位移将远小于普通抗滑桩。

综上，当排距约小于1.5d时，门架式双排抗滑桩就相当于将两根普通抗滑桩简单的叠加在一起而承受滑坡推力的作用；随着排距的增大，其结构自身的空间性也逐渐体现出来。当排距大于1.5d时，门架式双排抗滑桩结构具有一定的空间性，桩身的最大位移逐渐减小，当排距在2.5d～5d时，门架式双排抗滑桩的桩身位移最小，桩身位移的变化趋势不明显，其结构的空间性最好；当排距大于5d时，门架式双排抗滑桩的空间性将随着排距的增大而逐渐减弱。

由表2可知，当排距约小于1.5d时，前排桩的最大正弯矩大于后排桩，而当排距大于1.5d时，后排桩的最大正弯矩大于前排桩；造成这种变化的主要原因是由于结构自身的空间性，当排距大于1.5d时，后排桩主要承受抗拔力,而前排桩主要承受抗压；而后排桩的最大负弯矩大于前排桩。当排距约小于3d时，前后排桩的最大正弯矩变化较快，而前后排桩的最大负弯矩变化相对较慢；当排距大于3d时，前后排桩的最大正负弯矩变化均较慢。此外，从表2还可以看出，前排桩的最大正负弯矩随着排距的增大而逐渐减小；后排桩的最大正负弯矩随着排距的增大而逐渐增大。

同时,利用ANSYS分析桩体两侧的土压力的分布情况说明：当排距大于2.5d～5d时，前后排桩体受到的土压力比较合理，但当排距大于6d时，前后排桩的最大位移又将随着排距的增大而增大。

综合前、后排桩的最大水平位移和最大正、负弯矩的对比可以发现，桩体的最大水平位移发生在后排桩，且排距大于2.5d时，前后排桩的位移变化较缓，且前后排桩的位移相差较小，这样能充分发挥前后排桩的材料性能；当排距为5d时，前后排桩的最大位移取最小值；同时当排距在(3～5)d时，前后排桩的负弯矩相对较小，工程造价相对较低。因此，通过对比分析，当排距为(2.5～5)d时，门架式双排抗滑桩自身结构的空间性较好，能充分发挥其结构的优点；从经济和安全角度考虑，门架式双排抗滑桩的排距一般为(2.5～5)d。

3.2 连梁刚度对门架式双排抗滑桩的影响

连梁是指将前后排桩联结起来的桩顶横梁，它和前后排桩组成一空间结构，因此具有很大的刚度，并在一定程度上能对前后排桩的受力进行调整，减小桩顶位移；实践证明[4]，门架式双排抗滑桩和连梁之间存在着良好的协同工作能力，在协同工作下，能使前后排桩充分参与工作并提高整个结构的稳定性和安全性。本文将利用计算模型，在保持结构其他因素不变的情况下，根据算例取排距为4d，连梁刚度分别为0.25EI、0.5EI、1.5EI、2EI、2.5EI、3EI、4EI来进行分析。通过计算，其前后排桩桩身的最大位移、弯矩如表3、表4所示。

表3 前后排桩最大位移Smax mm

表3 前后排桩最大正负弯矩Mmax kN·m

由表3可知，随着连梁刚度的增大，前后排桩的最大位移逐渐增小；当刚度小于1.0EI时，减小速率较快，当刚度大于1.0EI时，减小速率较慢。以后排桩为例，从表3可以看出，当连梁刚度由0.25EI增大到1.0EI时，桩身的最大位移由24.23mm减小为19.43mm，减小了4.8mm；当连梁刚度由EI增大到2EI时，桩身的最大位移则由19.43mm减小为18.48mm，减小了0.95mm；从这可以看出，当连梁的刚度大于1.0EI时，其值的变化对后排桩桩身位移的影响可以忽略不计。

由表4可知，后排桩的最大正负弯矩随着连梁刚度的增大而减小，前排桩的最大正负弯矩随着连梁刚度的增大而增大；当连梁刚度小于1.0EI时，前后排桩的最大正负弯矩变化都比较明显，而当刚度大于EI时，其变化趋势逐渐减慢。以后排桩的最大正弯矩为例，当连梁刚度由0.25EI变为1.0EI时，其最大正弯矩由25 789kN·m减小为23 964kN·m，减小了1 825kN·m；当连梁刚度由1.0EI变为2EI时，其最大正弯矩由23 964kN·m减小为22 377kN·m，减小了1 587kN·m。

综上，当连梁刚度大于1.0EI时，其刚度的变化对桩身位移和弯矩的影响都不明显，在工程中，并不是连梁的刚度越大，其桩身位移和弯矩就越小，一味的提高连梁刚度只会造成资源的浪费；从设计和施工角度来说，为了考虑安全和经济的因素，本文认为连梁刚度、截面尺寸应和桩身一致。

3.3 桩间土的作用对门架式双排抗滑桩的影响

门架式双排抗滑桩桩间土通过与前后排桩的位移协调影响土压力在前后排桩间的分配，进而影响前后排桩共同工作的能力。本文将采用土弹簧来模拟桩间土的作用，通过改变土体的变形模量来改变土弹簧的刚度，从而分析桩间土对前后排桩的作用。本文将利用计算模型，在保持结构其他因素不变的情况下，取排距为4d，桩间土的变形模量分别为5MPa、10MPa、15MPa、20MPa来进行分析。通过计算，其前后排桩桩身的最大位移、弯矩如表5、表6所示。

表5 前后排桩最大位移Smax mm

表6 前后排桩最大正负弯矩Mmax kN·m

由表5可知，当桩间土的压缩模量由5MPa变为10MPa时，前后排桩身位移变化比较明显，当桩间土的压缩模量由10MPa变为20MPa时，桩身位移变化不明显。以后排桩为例，当桩间土的压缩模量由5MPa变为10MPa时，后排桩的最大位移由21.28mm变为19.43mm，减小了1.85mm；当桩间土的压缩模量由10MPa变为20MPa时，后排桩的最大位移由19.43mm减小为18.69mm，减小了0.74mm。

由表6可知，随着桩间土的压缩模量逐渐增大，后排桩的正负弯矩逐渐增大，而前排桩的正负弯矩逐渐减小，表明当改变桩间土的压缩性可以改变桩间土对前后排桩的作用。

在设计过程中，若忽略滑动面以上的桩间土作用，则门架式双排抗滑桩的有限元模型变为图3所示。

经计算分析，若忽略滑动面以上的桩间土作用，将使前后排桩的位移稍大于考虑桩间土作用时的情况。从而说明门架式双排抗滑桩滑动面以上的桩间土体对前后排桩具有一定的作用，但前后排桩的桩身位移变化并不大；若忽略其对前后排桩的作用，则既可以简化设计过程，又对最后的计 个排序基本一致。通过工程实例分析，验证了所编制的事故树的合理性。

3.3 主要影响因素和相应的改善措施

(1)X5(溶洞填充沉积大量介质)、X10(地表水有较好的条件下渗)、X9(与暗河连通，补给范围广)等都属于不良地质条件，要降低其对工程施工的影响，应加强地质勘探和超前预测预报工作，争取对前方地质情况有较详细的了解。

(2)X1(施工组织混乱)、X2(超前预测预报存在盲区、X3(注浆加固方案存在缺陷)等应加强施工人员的培训和管理，增强安全意识，及时监测和支护。

4 结论

通过以上对隧道突水突泥的事故树分析，可得出如下的结论：

(1)岩溶隧道突水突泥发生的原因复杂，影响事故的因素众多，通过一般方法难以对导致突水突泥的各种因素及其之间的逻辑关系做出系统的阐述。直观、逻辑性强的事故树是分析隧道突水突泥事故比较有效的方法。

(2)隧道突水突泥事故树中考虑17个基本事件，通过对事故树进行定性分析，明确了事故发生的主要潜在因素，并对相关影响因素进行重要度排序。最后结合工程实例，统计出各基本事件发生的概率，求出各基本事件的概率重要度和临界重要度，使相关的分析更加准确和可信，并提出了一些可行的建议和改进的措施。

[1] 周建昆.岩石公路隧道塌方风险事故树分析[J].地下空间与工程学报,2008,(12):991-998

[2] 孙伟亮.棋盘石隧道溶洞突水成因分析及技术处理措施[J].铁道建筑,2010,(10):54-56

[3] 王双龙.八卦山隧道突水突泥段处理技术[J].山西交通科技,2009,(4):54-60

[4] 曾强云.宜万铁路马鹿菁隧道水文地质分析及涌水预警[J].土工基础,2012,(4):35-37

[5] 仇海生,杨春丽.煤矿水灾的事故树分析法[J].煤矿安全，2008,(6):126-128

[6] 中华人民共和国建设部.地铁及地下工程建设风险管理指南[M].中国建筑工业出版社,2007