高墩大跨度连续刚构桥温度分布及效应分析

胡安庆，唐 英，张三峰

(中铁西南科学研究院,四川成都610031)

随着高等级公路建设的飞速发展，高速公路建设逐步进入山区，许多高墩大跨预应力混凝土连续刚构桥由于自身得天独厚的优点尤其受设计者所青睐。但对于多次超静定的连续刚构桥来讲，因墩梁固结，使得不论是上部结构梁体整体温差、日照温差还是桥墩的温差，均对全桥的内力分布及变形有重要影响。温度应力是引起桥梁开裂的重要原因之一，其中日照作用产生的温差荷载要比长期缓慢的年气温荷载影响更大[1]，由于桥墩受山体及桥梁上部结构遮荫等因素的影响，分析计算十分复杂。温度作用效应已成为高墩大跨度桥梁设计的控制因素之一，目前规范上也缺乏对桥墩温度分布的相应规定，人们对高墩大跨度桥梁墩部和梁部的温差分布及整体效应方面研究得较少。

本文以雅西高速公路腊八斤沟特大桥为例，根据收集的气象及地理资料，对预应力混凝土连续刚构桥的温度分布进行计算，确定桥梁最不利温差以及此时桥梁整体的温度分布情况，进而对该桥的温度效应进行分析。

1 温度分布与温度效应的分析方法

用热传导微分方程求解。热传导的过程是依靠物体内外的温度差而产生的，所以在研究热传导过程中，必须知道物体内的温度分布。一般说来，物体内的温度分布是空间与时间的函数，即：

Ti=f(x,y,z,t)

(1)

式中：x、y、z为空间直角坐标；i为时间；Ti为温度。

某点温度T，不仅与x、y、z坐标有关，而且与时间也有关，因此对于各向均质、同性的固体，由Fourier热传导理论可得无内热源时的三维不稳定导热方程：

(2)

式中：λ为混凝土的导热系数；c为混凝土的比热；γ为混凝土的容重。

在热传导初始瞬时，温度场坐标(x，y，z)的已知函数为Ti=f(x,y,z,t)，初始条件即混凝土结构的初始温度状态，或作为分析用的某一种特定温度分布状态，一般可以选择在混凝土结构整体温度分布较为均匀的时刻，即当t=0时，T0=f(x,y,z,0)，T0为一常数。

边界条件的问题可采用近似数值分析方法、半经验半理论公式等解法进行求解[2-3]。方程常用的边界条件有三种边界条件，一般采用第一类或第三类边界来求解。第一类边界需要现场测试混凝土表面温度，对于扑捉极值情况，费时费力，因此不实用。可以采用第三类边界来理论模拟分析桥墩的边界受太阳辐射和与大气辐射、对流换热过程。对混凝土边界，第三类边界条件，当混凝土与空气接触时，经过混凝土表面的热充量与混凝土表面温度T和气温Ta及日辐射关系为：

(3)

式中：β为表面总放热系数;Tw为外气温;as为结构表面日辐射热量吸收系数;S为日辐射强度。

S和Τw可按搜集的实际气象资料归纳成近似半正弦和正弦曲线代入[4]，当研究箱梁、桥墩内表面时，β则应取内部综合放热系数，Tw为内部空间气温，S=0。

在完成桥梁温度分布的分析，接下来将进行桥梁温度效应的分析，混凝土箱梁受太阳辐射引起的温差应力包括自应力和次应力两部分。自应力即在非线性温度梯度的日照温差作用下，因墩梁各纵向纤维的变形受到截面整体变形的约束而产生的自相平衡的纵向约束应力。而当墩梁的温差变形受到超静定结构体系的多余约束阻碍时，便产生温度二次力，相应的截面应力即次应力[5]。目前，许多大型有限元软件可用于计算分析桥梁的温度效应，如Midas、ANSYS等。

2 工程算例及分析

2.1 工程概况

腊八斤沟特大桥为雅西高速公路上跨度最大、墩高最高的一座预应力混凝土连续刚构桥，其位于地质条件复杂山岭重丘区，引桥部分为简支梁，主跨为4跨预应力钢筋混凝土连续刚构桥，主桥跨度为105 m+200 m+200 m +105 m，采用三向预应力结构的单室箱型截面箱梁。箱顶板宽12.1 m，底板宽6.8 m,根部断面和墩顶0号梁段高为12.75 m，跨中及边跨现浇段梁高3.80 m。主墩采用分幅式钢管混凝土叠合柱，最高墩高182.5 m，钢管内灌注高强混凝土(图1)。

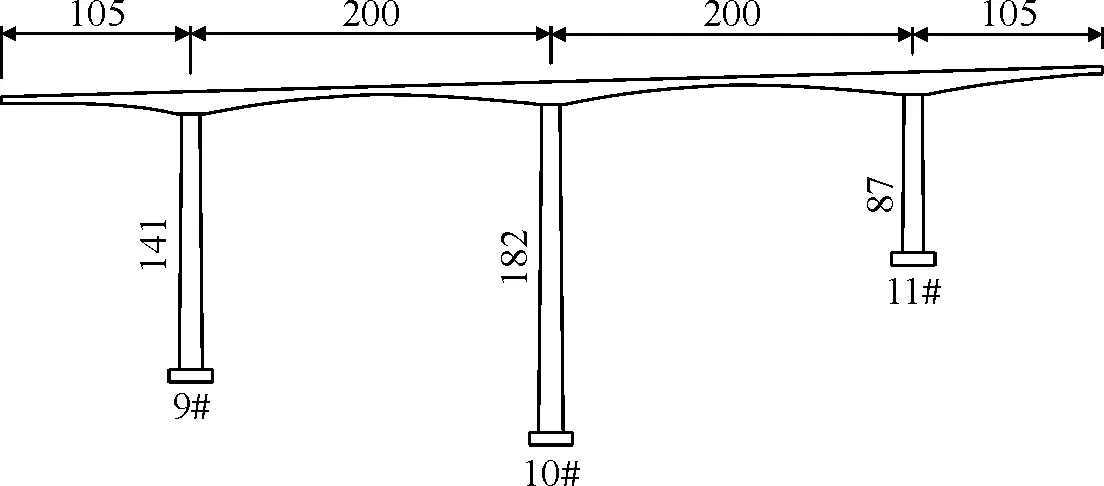
图1 主桥桥型示意(单位： m)

2.2 桥墩温度场计算分析

对于混凝土箱梁的温度场模式的选取，国内外规范繁多，且不尽相同，国内公路桥规和铁路桥规也不相同。而桥墩的温度分布模式，规范中没有具体规定，桥墩与箱梁的温度分布组合问题，国内外文献均少见分析，如果单一的对桥梁及桥墩都同时按规范箱梁的控制温差取值，显然不合理。文中在计算中考虑山体对桥梁的遮挡及桥梁上部结构对桥墩的遮荫效应，通过收集桥址处的地理信息及1988年～2006年时的气象资料，来分别计算确定箱梁和桥墩的温度场模式。

桥梁的不利的瞬时温度场，存在桥墩最大温差时刻的全桥温度场和箱梁最大温差时刻的全桥温度场两种情况。对于温度变位来说，多跨连续刚构桥由箱梁温度变化引起墩顶的纵向变位。远大于由桥墩温度变化引起的纵向变位。限于篇幅，重点分析箱梁最大温差时的全桥温度效应。

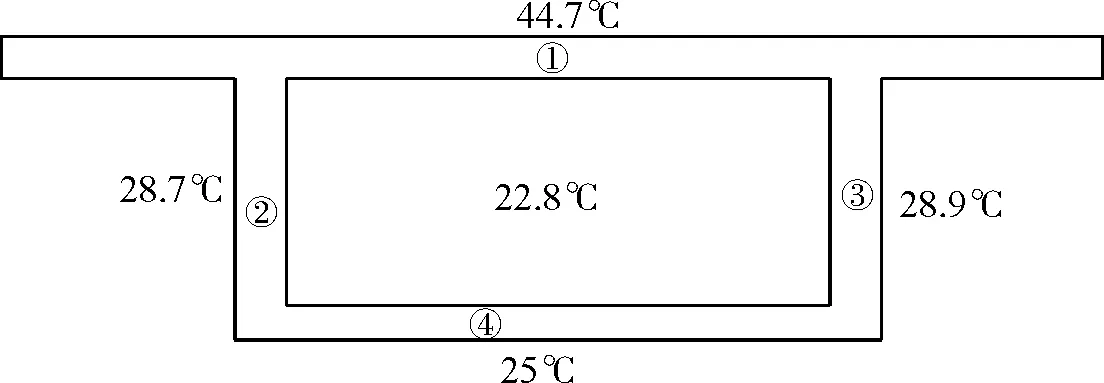
为便于分析，对箱梁及桥墩的4个壁板进行编号,根据热传导理论编制程序，计算出箱梁的24 h温度场变化情况，分析提取箱梁的最大温差[1]，可以得到在6月2日在14：00时，箱梁顶板温差最大，此时墩、梁温度分布见图2、图3。

A箱梁

B桥墩图2 箱梁温差最大时刻箱梁、桥墩温度分布

图3 箱梁各板温度分布

由图2、图3可知：箱梁顶板上温度达到44.7℃，内部表面为22.8℃，在顶板上的温差最大，为21.9℃。2#腹板向东面，在14：00时已经不受太阳的照射，但是该壁面已经受到太阳升起一段时间内的照射，且历时较长，热量已经向混凝土内部传导，其总体温度较高。而面向西的3#腹板，表面刚开始受到太阳照射，其表面的温度迅速上升，略高于2#腹板的表面温度，但是其表面的热量并未传到其内部，因此3#腹板的内部温度与底板温度接近，底板始终没有太阳的照射，只随气温的变化而有所变化，因此其温度最低。各壁面上的所有温度值，计算温差，对温差采用e指数进行拟合，便可得到其温差曲线表达式。顶板温差拟合得到：T=21.9e-6.4x，式中x为混凝土外壁到计算点的距离。箱梁其它板壁上形成的温差分别是：5.9℃、6.1℃、2.2℃。

此时在桥墩的1#、2#、3#、4#板壁上形成的温差分别是：4.4℃、4.8℃、10.1℃、10.4℃，所产生的温差不大，分析温度效应时应用此时的箱梁、桥墩温差组合进行。

2.3 温度效应分析

对该桥的主跨(9#～11#墩)，采用有限元软件Midas建模，将计算得出的箱梁温差最大时刻的全桥温度场，输入模型，计算分析出桥梁的温度效应(图4、图5)。

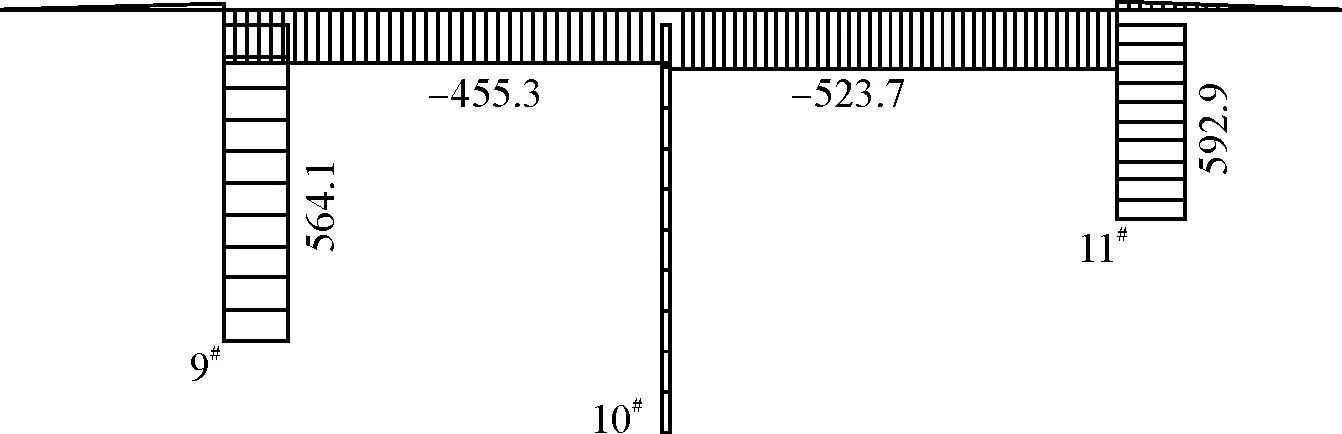
图4 全桥轴力图(单位：kN)

图5 全桥弯矩图(单位：kN·m)

对于连续刚构桥，其温度影响的主要部位为箱梁0#块及跨中部位，跨中截面较弱，将出现最大拉应力。

由图6可知，由温度引起的箱梁顶部受压应力，其最大压应力为-8.39 MPa；最大温度应力出现在中部箱梁的的腹板内壁，最大达1.83 MPa。

由图7可知，该时刻全桥温度变形情况为：竖向(Z轴)变形情况为，在9#、10#墩和10#、11#墩的跨中部位引起下挠，下挠值为6 mm，在8#、9#墩和11#、12#墩间的箱梁发生向上位移，上挠值为4 mm。横向(X轴)变形情况为：左右两边梁端各向两端伸长10 mm、6 mm，9#墩向左偏位7 mm，11#向右偏位3 mm，由于10#墩两边的9#和11#墩刚度不一致，因此，10#墩也有一定横向位移，向左偏移2 mm。

图7 全桥温度变形(单位：mm) (阴影为变形前)

4 结束语

根据腊八斤沟大桥所处地理位置及收集到的气象资料，通过对桥梁的温度分布及产生的温度变形和温度应力进行详细的分析研究，可以得到以下几点结论：

(1)在箱梁上，沿梁高方向的最大正温差为21.9℃，分布曲线为T=21.9e-6.4x。此时，桥墩的4块板壁上形成的温差分别是：4.4℃～10.4℃，温差不大。

(2)日照引起混凝土表面温度升高的同时，也使得表面压应力增大，该桥顶板最大压应力可达-8.39 MPa，腹板及底板受拉，最大温度应力出现在跨中箱梁的腹板的内壁，最大达1.83 MPa。

(3)在箱梁最大温差时刻，该连续刚构桥的温度效应为：在跨中部位引起6 mm下挠，在边跨处箱梁出现向上位移，各桥墩也有一定的横向位移，最大达7 mm。

由此可见，温度变形和温度应力在高墩大跨度桥梁的设计及施工控制中占的比重较大，应该引起足够重视。

[1] 刘兴法. 混凝土结构的温度应力分析[M]. 北京:人民交通出版社,1991

[2] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京：中国电力出版社，1999

[3] 管敏鑫. 混凝土桥梁的日照温度荷载、温度应力的计算与裂纹[J].中国铁道科学， 1986，(2)

[4] 管敏鑫. 混凝土箱梁温度场、温度应力和温度位移的计算方法[J].桥梁建设， 1985，(1)

[5] 张元海，李乔.桥梁结构日照温差二次力及温度应力计算方法研究[J].中国公路学报，2004，(1)