基于变系数α-β-γ滤波的目标跟踪仿真研究

基于变系数α-β-γ滤波的目标跟踪仿真研究

针对目标跟踪中联合数据关联算法计算量大，随目标数目增多呈几何增长而导致跟踪效率低下的问题，主要介绍了顺序数据关联快速算法（MSFAFDA），建立了基于变系数α-β-γ滤波和顺序数据关联快速算法的模型，并进行了模拟战场实际目标的仿真试验。仿真结果表明该算法能较好的跟踪目标，其跟踪精度符合要求，提高了跟踪实时性。

仿真；目标跟踪；变系数α-β-γ；滤波

在现代战争中，利用多种传感器对目标进行跟踪和识别是获取战场情报的主要手段之一。多目标跟踪的任务是利用传感器获得的观测信息，对目标进行精确的当前状态估计和以后状态预测。多目标跟踪包括跟踪门的形成，数据关联、跟踪起始与终结等环节，其主要标志是数据关联与滤波理论的有机结合，正确地判定量测信息的来源是有效维持目标跟踪的关键[1]。由于各传感器观测数据存在系统误差，传至融合中心数据存在平移和旋转等变化，在融合中心航迹关联一旦关联错误，将产生错误的目标航迹，使得真实目标航迹丢失。因此，建立准确的目标航迹和战场态势，在多目标跟踪过程中，尤为重要[2]。

1 变系数α-β-γ滤波方程

预测方程：α

j∑

变系数α-β-γ滤波器具有较好的跟踪性能，能跟踪机动目标[3]。

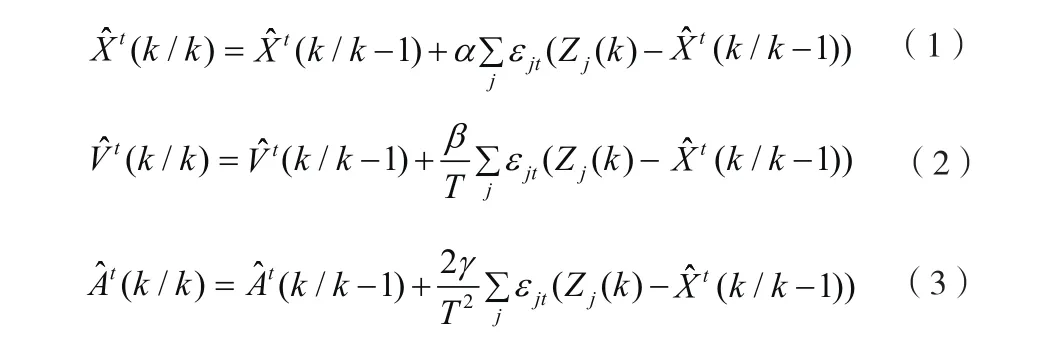
滤波方程：αε（ （） （/ 1））− −

∑

2 顺序数据关联快速算法

Z k X k k

t Z k X k k

jt j j

t（ （） （/ 1））− −

∑

αε

jt j j

在多目标密集的环境中，由于JPDA算法的关联概率的计算量随密集回波个数的增加而呈指数增长，明显影响计算速度，因而不适于实时跟踪密集回波下的多个机动目标[4]。由于数据关联快速算法（FAFDA）的计算量随密集回波个数的增加只呈线性增长，其实现实时跟踪的速度明显优于JPDA算法[5]，其跟踪精度也满足要求，在此基础上，构造顺序数据关联快速算法（MSFAFDA），具体步骤如下：

1）确定量测点j与己知目标t互联的所有简单事件，计算量测j落入目标t跟踪门内的概率Pjt（k）[6]：其中：λ杂波密度；PD为雷达检测概率；N[djt（k），0，St（k）]为正态分布密度函数。

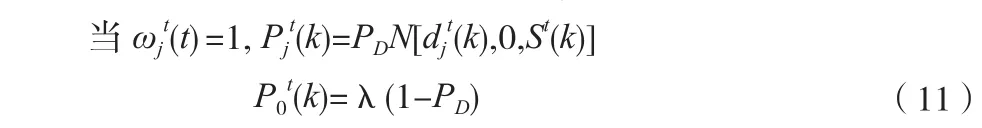
2）对第一个传感器确认量测。对第一个传感器的所有量测 Z1.j（k），利用椭球门来确认是否为t目标的有效回波[7]。

3 仿 真

k Z k X k k（）[ （） （/ 1）]（）k− −

∑ε k k k Z k X k k

t

t

^

jj =

1， 1 0（/ 1） （）[ （） （/ 1）]−+ − −

∑

^

m k

t

t（）[ （） （/ 1）] k（）1（）ε

1， 1 0

^

t

jj =

jj j=

αε

t k Z k X k k− −

∑

1， 1 0 1）]− 1）]

在此仿真中，模拟两部雷达获取观测数据，采用变系数α-β-γ滤波和顺序数据关联快速算法对目标进行跟踪和关联。

3.1 具体参数设置

扫描周期：T=5 s；雷达观测噪声标准差是：σv=0.4 km；雷达检测概率：PD=0.99；落入关联门概率：P＝0.99；杂波密度：λ＝0.05 km2；尺寸因子：K＝3.034 9；

3.2 仿真结果及分析结论

本仿真中，为简化计算，假设跟踪3个地面运动目标，跟踪期间目标数目无变化且各自的航迹确定。采用MSFAFDA和FAFDA算法，对相同目标进行仿真。

由于观测轨迹与跟踪轨迹之间的差值太小，为便于在图中观看和比较，把观测轨迹与跟踪轨迹之间的差值扩大了10倍。

由图1可以看出，根据上述两种算法计算出的目标航迹与观测轨迹趋势一致，这说明了这两种算法具有收敛性。

由图2、3误差对比可以看出，MSFAFDA算法计算出的数据平均误差小于FAFDA算法计算出的数据平均误差，跟踪精度有所提高。在MSFAFDA算法中，跟踪目标的最大误差是0.056 5 km，FAFDA算法中，跟踪目标的最大误差是0.179 9 km，跟踪总趋势与真实轨迹一致。从耗时上看，MSFAFDA算法所用时间略大于FAFDA算法所用时间。跟踪误差变大，是因为多个目标航迹进行交叉或目标密度变大时所致，随着目标密度变小或目标航迹不交叉时，误差又会逐渐变小（限于篇幅，仿真了3个运动目标，本文只列出了其中1个目标航迹示意图）。误差对比如图2～图3所示。

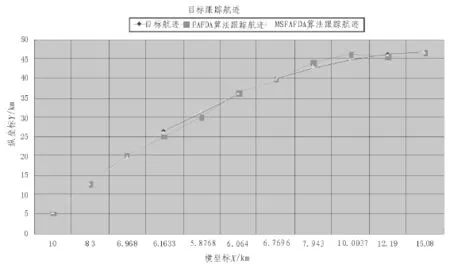
图1 目标观测轨迹与跟踪轨对比图Fig.1 Comparison of observation and tacking trajectory

图2 X坐标误差对比示意图Fig.2 Comparison of error among x coordinate

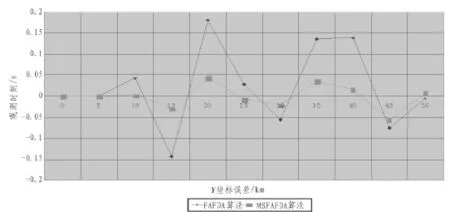
图3 Y坐标误差对比示意图Fig.3 Comparison of error among y coordinate

4 结束语

文中简要介绍了顺序数据关联快速算法、变系数α-β-γ滤波方程，并进行了仿真验证实验，仿真结果验证了该算法的有效性。

[1] 刘同明，夏祖勋，解洪成.数据融合技术及其应用[M].北京：国防工业出版社，1998.

[2] 王圣东，管飞，陈林元，等.多目标环境下基于分布式融合思想的误差估计方法 [J].指挥控制与仿真，2013，35（4）：131-137.

WANG Sheng-dong，GUAN Fei，CHEN Lin-yuan，et al.Algorithm for bias estimation base on distribution Fusion in multi-target environment[J].Command Control ＆ Simulation，2013，35（4）：131-137.

[3] 扬万海.多传感器数据融合及应用[M].西安：西安电子科技大学出版社，2004.

[4] An improved multiple model GM-PHD filter for maneuvering target tracking[J].Chinese Journal of Aeronautics，2013，26（1）：179-185.

[5] 高倩.基于信息融合的多传感器多目标跟踪算法研究[D].烟台：鲁东大学硕士论文，2012.

[6] 李树军.基于数据关联快速算法的目标跟踪与仿真研究[J].红外技术，2008，30（5）：268-270.

LI Shu-jun.Research on targets tracking using Fast algorithm for data association and simulation[J].Infrared Technology，2008，30（5）：268-270.

[7] 林亦宁.基于广义Hough 变换的目标跟踪算法研究[D].杭州：浙江大学，2013.

李树军，赵育良，王淑娟

（海军航空工程学院青岛校区 航空仪电控制系，山东 青岛 266041）

Algorithm research of targets tracking based on variable coef fi cient α-β-γ fi lter

LI Shu-jun，ZHAO Yu-liang，WANG Shu-juan
（Department of Aerial Special Equipment，Qingdao Campus of NAEI，Qingdao 266041，China）

Sequential Fast Algorithm for Data Association was introduced in allusion to problem of inefficient targets tracking induced by a mass of calculation with sensors.Based on coefficient α-β-γFilter and MSFAFDA model was established.At last，simulation experiment for targets in battlefield was conducted，which validates that the algorithm in real-time track targets and tacking precision was up to the mustard..

simulation；targets tracking；coefficient α-β-γ；filter

TP391

A

1674-6236（2014）11-0152-03

2013-09-11 稿件编号：201309089

李树军（1973—），男，山东莱芜人，硕士研究生，讲师。研究方向：目标跟踪与识别、仿真。