多目标优化问题的遗传算法改进研究

马昌威

（阿坝师范高等专科学校 计算机科学系，四川 汶川 623002）

多目标优化问题的遗传算法改进研究

马昌威

（阿坝师范高等专科学校 计算机科学系，四川 汶川 623002）

基于Nash均衡的思想在NSGA所求得的Pareto最优解基础上，探讨一种能对多目标优化问题进行求解的遗传算法。采用Nash均衡的思想在多目标优化的遗传算法，结合NSGA算法，提出一种能得到多个Pareto最优解的多目标优化算法。通过目标函数线性加权法、NSGA对函数进行了试验分析，对部分自变量进行固定，对其他的自变量进行优化，对Pareto最优解进行持续优化，进而实现 加速算法的收敛，从实验中得出了这种算法具有较快的收敛性，但是其运行时间和NSGA相比没有多少改善。

遗传算法；多目标；博弈论；Nash均衡；最优解集

多目标优化问题的起源是实际中复杂系统设计、建模与规划问题，这些系统所在的领域包含了生产、生活中的方方面面。在现实生活中几乎每一个决策问题都必须要考虑如何在不同的约束条件下同时处理多个相互冲突的目标，这些问题都涉及到了多个目标的优化，在这些问题中各个目标并不是单独独立存在的，往往是混合在一起相互竞争的目标，每一个目标都具有不同的意义与方法，而它们之间所存在的竞争性与复杂性使得优化变得相当困难。在多目标优化问题的解决中，遗传算法是一种较为有效的方法。同时遗传算法将决策者纳入到了问题的讨论范围中，使得决策更加的合理。

1 多目标遗传算法

在过去的多年中，作为多目标优化问题的新求解方法，遗传算法受到了较大程度的关注，进而诞生了遗传多目标优化。传统的多目标优化方法有约束法[1]、加权法、距离函数法[2]、分层序列法[3]等。而传统的方法却存在一定的缺陷[3-4]，这些缺陷的存在促使了遗传算法的发展。

将遗传算法的思想运用到多目标优化问题中最早可以追溯到1967年，Rosenberg在其研究中模拟单细胞有机物的化学遗传特性时采用的多属性研究方法[5]，并且提到了可考虑利用遗传的搜索算法对多目标问题进行求解。虽然最后他只是采用了单一属性方法，但是其研究却是开创了遗传算法应用到多目标优化领域中的先河。

20世纪90年代，遗传算法开始在多目标优化领域中正式运用。在90年代多目标遗传算法主要分为两类，其中一类是采用Pareto机制的多目标演化算法[6-7]，这种算法是当前研究中的热点，而另外一类则是非Pareto机制的多目标演化算法[8]。

1985年，David Schaffer为了能给对整合方法的缺点进行改进，在Grefenstette 的单目标优化程序GENESIS的基础上提出了一种基于向量评估的遗传算法（VEGA）。这是第一种多目标不演化算法。但是这种方法并不是基于Pareto。1993年，Hom与Nafpliotis提出了一种基于Pareto的锦标赛选择机制方法——小组决胜遗传算法。

随着多目标演化算法在各个领域中的应用越来越广泛，对其所进行的研究也基本是直接受实际工程问题推动的[9-11]。当前在多目标优化技术方面还存在很多需要解决的困难与问题，例如非劣最优解域收敛性分析、种群更新终止条件及其稳定性分析等的。

2 基于博弈论的多目标遗传算法

博弈论所研究的是决策主体的行为发生直接的相互作用时决策以及这种决策的均衡问题。在博弈论中研究的典型问题是两个或者两个以上的参加者在某种对抗性或者竞争性的情况下各自做出决策，让自己的一方可以最大限度的得到最有利的结果。博弈就是一组规则，整个过程中都有需要遵循的办法与章程，包括了局中人、策略、选定策略后的结局等等都需要符合规则。接下来就将博弈论用于多目标优化问题进行探讨。

2.1 Nash均衡与博弈论

在博弈论中所研究的对象是多个决策主体之间的相互作用，也就是决策主体具有相互依存性，在博弈中任何一个决策主体都会受到其他决策主体的影响，同时每一个决策主体的决策都会影响到其他的主体。

1）博弈要素

博弈的要素主要有参与人、策略以及效用函数。

参与人指的是参与博弈的决策主体，同时也被称为局中人，用Yi（i=1，2，…，n）表示。

策略指的是每一个参与人可以做出的行动。

纯策略集，指的是每一个参与人通常会有多个策略进行选择，这些策略构成了这个参与人的纯策略集，参与人Yi（i=1，2，…，n）的纯策略集用Si={Si1，Si2，…，Simi}进行表示，其中mi则是表示第i个参与人可以选择的策略个数。

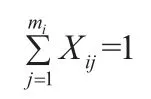
局势，指的是博弈中参与的各方所采取的策略的组合，可以是纯策略的组合，记为 S=S1×S2×…×Sn，也可以是采取的混合策略组合，记为S=Q1×Q2×…×Qn。

效用函数，指的是局势集合S上的函数，主要是用来对博弈中的参与人盈利是多少，可以为参与人做出更加理性的决策提供重要的依据。当所有的参与人所做出的决策集合在一起时，就会引起相应的结果，着写结果能够反映出参与人的目标实现的具体情况，因此，就存在一个对客观现实进行反映的映射：Fij（s）→R1，s∈S，（j=1，2，…，ki）。在这个式子中，Fij代表的是第i个参与人的第j个目标函数，ki则是表示第i个参与人做考虑的目标个数，那么参与人 的效用函数就可以记为：

F1=（Fi1，Fi2，…Fik），i=1，2，…n

记Y1=（Y1，Y2，…Yn），F1=（F1，F2，…Fn），用G=（Y，S，F）来对博弈的策略模型进行表示。

2）Nash均衡

Nash均衡又被称为合作博弈均衡，是博弈论中的一个相当重要的术语，是数学家Nash在1954年提出的。其定义是：假设在博弈中有n个人参与其中，如果在某种情况下没有一个参与者能独自行动而使得收益得到增加（也就是为了自身的利益达到最大化，没有任何一个单独的一方愿意对其策略进行改变），那么这种策略组合就被成为Nash均衡。Nash均衡从实质上来讲，是一种非合作博弈的状态。当Nash均衡达成时，并不代表博弈的各方都是处于一种不同的状态，而是在顺序博弈中这个均衡在博弈者的连续动作与各种反应中大程度的。Nash均衡并并不是代表博弈的各方达到了整体的最优状态。

Pareto-Nash均衡是多目标博弈中的均衡，这个概念也被称为有效Nash均衡策略。这种策略是博弈中的众多策略中的一个“不坏”的策略，因此，其又被称为非劣Nash均衡策略。因此，通常情况下，并不会像单目标博弈中的那样唯一的或者不多的几个Nash均衡策略，而是往往存在多个Pareto-Nash均衡策略。而全部的Pareto-Nash均衡策略所组成的集合则是叫做Pareto-Nash均衡策略。

2.2 算法改进

1）基本思想

这里在Nash Gas的基础上，结合NSGA算法，提出一种能得到多个Pareto最优解的多目标优化算法。

2）算法测试

为了能够进行比较，这里选取参考文献[12]中的函数来进行测试（这个问题是由Deb设计的[13]），描述如下

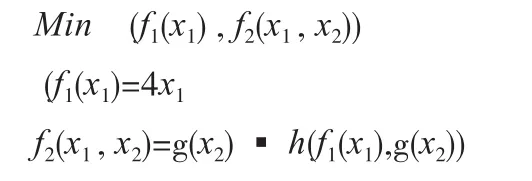
其中：

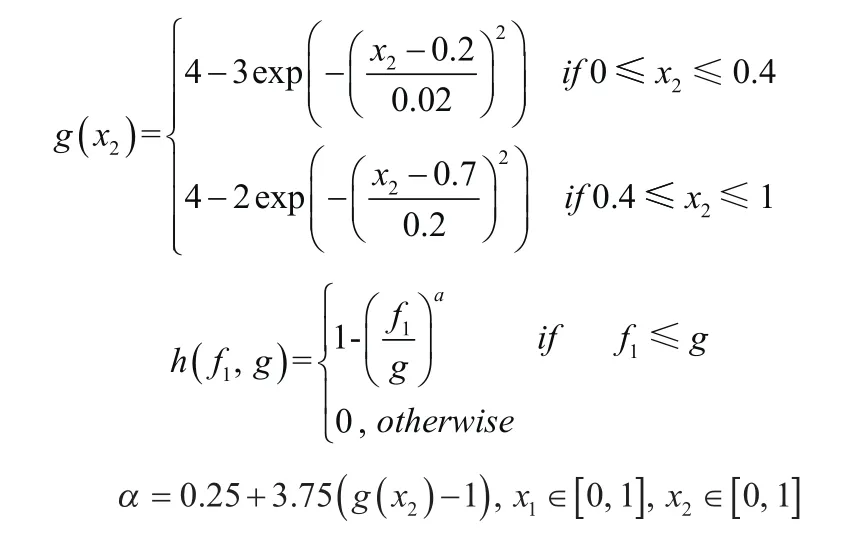
对这个问题分别使用目标函数线性加权法、NSGA与文中上述算法进行求解，其结果如下：

线性加权法：

运用线性加权法求解50次，结果如下：

3

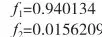
求解的过程使用的是实数编码方法，种群规模为20，最大进化代数则为2000.

NSGA算法：

使用实数编码、基于Pareto排序与共享机制的NSGA来对这个问题进行求解。种群的规模为50，在表1中显示了不同的进化代数，全局Pareto最优解在所有解中所占的比例。

表1 NSGA算法求解结果Tab.1 NSGA algorithm results

从表中能够看出，当种群规模为50时，该算法需要运行400代才能100％的保证收敛到最优解。

文中所述算法：

针对两目标、两自变量函数优化问题，将第一个目标函数来作为第一个参与人，对f1进行优化；将第二个目标函数作为第二个参与人，对x1进行固定，对f2进行优化，种群规模选定为50，分别使用线性加权法、NSGA与上诉的算法进行求解，得到如下结果：

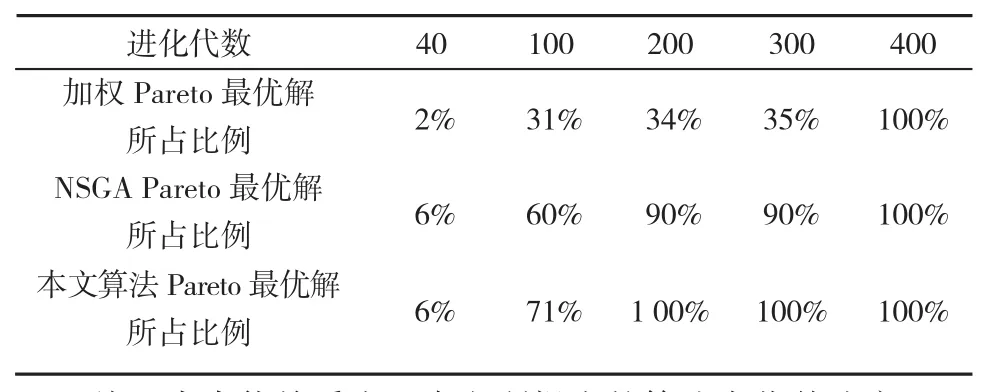
表2 不同Pareto算法的最优解所占比例Tab.2 Different Pareto optimal solution algorithms

从上表中能给看出，本文所提出的算法在收敛速度上比线性加权法与NSGA都要优秀，只需要200代就能够100％收敛到全局Pareto最优解。因为在NSGA中嵌入了Nash均衡的过程，因此算法的时间上与NSGA相比没有多少改善。

2.3 展 望

将Nash均衡的思想在多目标优化的遗传算法中进行运用，在这个算法中将优化对象中的每一个目标，对应到博弈中的一个参与人，将所有的自变量在这些参与人之间进行分配，其中每一个参与人分配的是自变量的一个子集。在优化的过程中，每一个局中人都通过遗传算法来对自己对应的目标进行优化，通过这样的方法来对NSGA方法继续优化得到Pareto最优解，并将Pareto最优解注入到NSGA的外部种群中，这样就能让算法快速收敛。

随着社会与科技的发展，很多问题的规模都在增大，使得组合优化问题的搜索空间也急剧的增加，有时在当前的计算上利用枚举法是很难找到最优解的。对于这种复杂的问题，人们已经意识到了寻求满意解的重要性，而遗传算法则是寻求满意解的最佳工具之一。遗传算法对于组合优化中的NP问题有着良好的效果，例如在求解旅行商问题、背包问题、工作日程安排、试题组卷问题、装箱问题、图形划分问题等很多方面，遗传算法都取得了一定的成功[14]。同时GA在生产调度问题、自动控制、机器人学、图像处理等很多方面都有着广泛的运用。

3 结束语

文中在Nash均衡的基础上，根据NSGA算法，提出了一种能对多目标优化问题进行求解的遗传算法，该算法使用Nash均衡的思想在NSGA所求得的Pareto最优解的基础上，对部分自变量进行固定，对其他的自变量进行优化，对Pareto最优解进行持续优化，进而实现 加速算法的收敛。从实验中能给出，这种算法具有较快的收敛性，但是其运行时间和NSGA相比没有多少的改善。

[1] 唐焕文，秦学志.实用最优化方法[M]，大连：大连理工大学出版社，2004.

[2] 高媛.非支配排序遗传算法（NSGA）的研究与应用[D].杭州：浙江大学，2006.

[3] 崔逊学.多目标进化算法及其应用[M].北京：国防工业出版社，2006.

[4] 周盛强，向锦武.基于BP网络和Pareto的遗传算法的多目标协同优化[J].机械设计与研究，2006，22（5）：10-13.

ZHOU Sheng-qiang，XIANG Jin-wu Based on BP network and Pareto genetic algorithm for multi-objective collaborative optimization[J].Mechanical Design and Research，2006，22（5）：10-13.

[5] 刘瑞，许峰.基于 支配擂台赛法则的多目标遗传算法[J].软件导刊，2012，11（8）：53-55.

LIU Rui，XU Feng.Disposable Challenge Cup rule based multi-objective genetic algorithm [J].Software Tribune，2012，11（8）：53-55.

[6] 高坚.基于免疫机制和遗传进化的网络组播路由优化算法[J].微电子学和计算机，2003，20（8）：20-21.

GAO Jian.Based on Immune Mechanism and Genetic network multicast routing optimization algorithm [J].Microelectronics and Computer，2003，20（8）：20-21.

[7] 孙强，杨俊茹.一种基于多目标遗传算法的高层次测试综合方法[J].计算机应用与软件，2013，30（5）：245-247.

SUN Qiang，YANG Jun-ru.A multi-objective genetic algorithm based on high-level test synthesis method [J].Computer Applications and Software，2013，30（5）：245-247.

[8] 李焕勤，钱展.解决混合装配线平衡问题的多目标遗传算法研究[J].河南科学，2012，30（6）：724-729.

LI Huan-qin，QIAN Zhan.Hybrid assembly line balancing problem to solve multi-objective genetic algorithm [J].Henan Science，2012，30（6）：724-729.

Improvement of genetic algorithm for multi-objective optimization problem

MA Chang-wei
（Dept.of Computer Science of Aba Teachers College，Wenchuan 623002，China）

Purpose of this paper the idea of Nash equilibrium based on NSGA Pareto optimal solutions are obtained based on the right to explore a multi-objective optimization problem can be solved genetic algorithms.Methods idea of Nash equilibrium in a multi-objective optimization genetic algorithm，combined with NSGA algorithm is proposed to get multiple Pareto optimal solution of multi-objective optimization algorithm.Results The linear weighted objective function method，NSGA tested for function analysis，on the part of the independent variable and fixed，for other independent variables are optimized for Pareto optimal solution for continuous optimization，thus achieving accelerated convergence of the algorithm，the conclusion from the experimental derive this algorithm has faster convergence，but its running time and NSGA little improvement compared.

genetic algorithm；multi-objective；game theory；Nash equilibrium；optimal solution set

TN01

A

1674-6236（2014）11-0145-03

2013-11-21 稿件编号：201311182

四川省教育厅2012年立项课题（12ZB001；12ZB169）

马昌威（1972—），男，四川茂县人，硕士，副教授。研究方向：计算机应用和高等教育信息化。