基于FPGA的GPS时钟驯服电路设计与实现

张 磊，黄海生，张 斌

（西安邮电大学 陕西 西安 710121）

基于FPGA的GPS时钟驯服电路设计与实现

张 磊，黄海生，张 斌

（西安邮电大学 陕西 西安 710121）

为满足系统对高精度时钟的要求，根据晶振时钟无随机误差和全球定位系统（GPS）时钟无累计误差的特点，提出了一种利用GPS秒时钟驯服晶振时钟来实现高精度时钟的方案。该方案根据数字锁相环倍频原理，通过测量GPS秒时钟和本地生成秒时钟的相位误差来调整电路分频比，实时消除晶振时钟的累计误差，从而实现高精度的系统时钟。经实际验证，该方法在使用16.369 M温补晶振时，在GPS信号有效情况下输出时钟误差小于0.1 ppm，GPS信号失效后1小时后误差小于0.3 ppm。

GPS秒时钟；时钟驯服；高精度时钟；时间同步；现场可编程门阵列

GPS是一个全球卫星导航定位系统，可以为用户免费提供实时、高精度的时间信息。GPS的时间系统由具有高精度、高稳定度的原子钟组成。由地面控制系统的氢原子或铯原子钟向主运行钟提供时间与频率微调参数，使主运行钟保持极高的长期稳定性，精度可以达到 10-12～10-15，没有累计误差[1]。

现代电力和通信系统等需要高精确的时钟系统，时钟系统精度要求达到 ，甚至纳秒级别。如何简单、低成本的获取高精度时间系统尤为重要。电子系统一般使用晶振作为时钟源，经分频后作为系统时钟。晶振随着使用环境温度、电压的变化以及时间的推移，频率会有一定的偏移，但晶振频率短稳特性好，无随机误差。针对以上问题，结合GPS时钟无累积误差和晶振时钟无随机误差的特性，采用一种使用GPS时钟同步晶振时钟，实现高精度同步时钟的方法。此方法使用GPS时钟实时测量晶振时钟频率以及输出时钟相位，利用晶振频差和输出时钟相位差调节电路分频比，消除晶振时钟累积误差的同时与GPS时钟保持同步[1-2]。

1 时钟误差分析

1.1 晶振秒时钟误差分析

对温补晶振时钟进行分频，可以得到系统需要的频率时钟。设晶振时钟频率为f，周期t。设系统需要的时钟频率为f0，周期为T0。则标准分频比为：

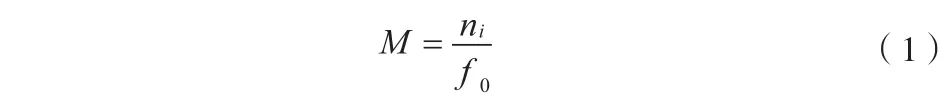
式中：ni为晶振时钟在一秒时间内的计数值。因为温补晶振在短时间内的频率稳定度很好，短时间内使用晶振分频得到的时钟频率随机误差很小。现连考察续晶振分频得到的时钟序列：T1，T2，T3，…，Tn，设观测的第一个时钟与标准时间（UTC）的偏差为 ▽t0，由于晶振时钟频差导致的每周期时钟偏差为为 ▽t1，对应每个时钟的误差是τ1，τ2，τ3，…，τn。则有：

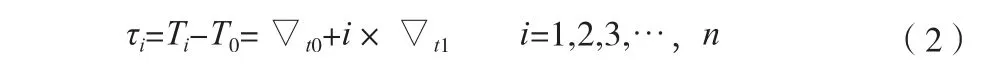
有（2）式可知，分频时钟在开始时误差较小，随着时间的推移，即 i值较大时，误差不断积累，误差显著增大。

此外，由于分频比可能是无限小数，系统分频不可能做到准确无误，分频比有一定的截断误差，也会给输出时钟增加误差。

1.2 GPS秒时钟误差分析

GPS的时间系统由具有高精度、高稳定度的原子钟组成。并由地面控制系统的氢原子或铯原子钟向主运行钟提供时间与频率微调参数，使主运行钟保持极高的长期稳定性，精度可以达到10-12～10-15，没有累计误差。

由于GPS信号受电离层延迟误差，对流层延迟误差，多径效应和接收机噪声的影响，接收机在正常工作时恢复出来的秒时钟信号也存在一定的误差，秒时钟误差服从正太分布，表现为恢复出的GPS秒信号相对于UTC时钟脉冲有左右漂移。设GPS接收机恢复出的秒时钟与UTC时钟误差为ε，ε为随机误差且服从正太，取样数N，有：

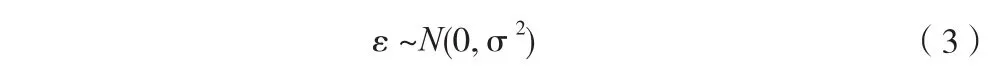
对于不同型号的接收机，对应的σ取值不同，一般在100 ns以内，如星际通GP5MX1513F1GPS为50 ns。

观察n个GPS秒时钟序列T1，T2，T3，…，Tn，假设每个秒时钟对应的随机误差为 ε1，ε2，ε3，…，εn，UTC秒时钟T0，有：

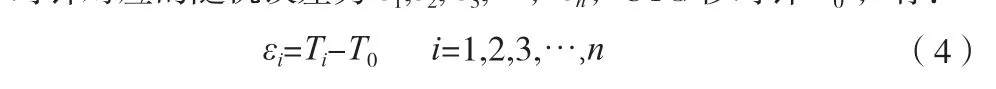
则有随机误差的平均值为：

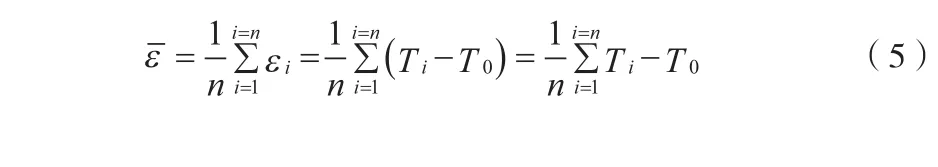
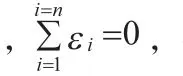
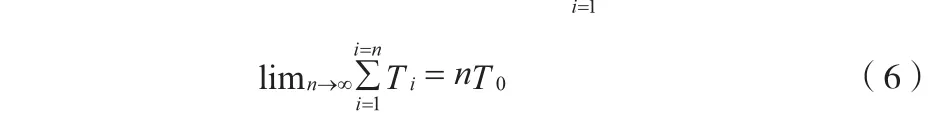
由以上分析知GPS秒时钟有一定的随机误差，误差随不同型号接收机变化大小不一；但时钟长时间的累积误差趋于零，即GPS秒时钟没有累计误差，可以将它作为标准时钟驯服晶振时钟来生成高精度系统时钟。

2 高精度时钟驯服原理

由于晶振时钟短期稳定性好，随机误差较小，而GPS秒时钟没累计误差较小，所以使用GPS秒时钟驯服晶振时钟，消除晶振时钟累积误差。对晶振时钟驯服有两种方法：一种是将晶振时钟误差转化为晶振对应的电压调节量，直接对晶振工作电压进行控制，从而调节晶振震荡时钟周期，使晶振时钟趋于一个标准值，这种方法优点是可以得到精确地晶振时钟，缺点是技术实现复杂，不易实现；一种是将晶振时钟误差转化为时钟分频调节量，对分频电路的分频比进行调节，得到高精确的分频时钟，这种方法优点是技术实现简单，缺点是需要更高频的晶振[3]。本文采用第二种方法，根据数字锁相环原理，以GPS秒时钟为基准，通过GPS秒时钟驯服晶振时钟实现系统需要的高精度时钟。

2.1 数字锁相环原理

数字锁相环的主要功能是使得输出信号和输入信号相位保持一个固定的关系，锁相环一旦进入锁定状态，输出信号和输入信号相位关系基本保持不变，只有很小的抖动误差，而没有频率误差[4]。本文基于这一原理实现高精度同步时钟，既能消除晶振时钟引起的累积误差，同时保持了较小的随机误差。

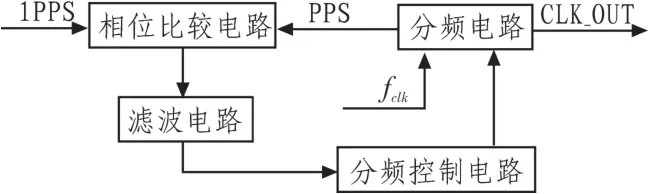
图1 数字锁相环原理框图Fig.1 Principle block diagram of digital PLL

2.1.1 相位比较电路

相位比较电路工作时钟为fclk，即系统晶振时钟。相位比较电路测量GPS接收机1PPS信号和本地晶振分频得到的PPS信号的相位关系，输出两者相位差值。接收机1PPS信号对于电路是一个异步信号，电路需要找出它的上升沿时刻，产生一个窄脉冲，窄脉冲同步于电路晶振时钟，窄脉冲的上升沿对应1PPS信号的起始时刻，在窄脉冲的上升沿处检测PPS信号的相位值。

2.1.2 滤波电路

由于GPS接收机输出的1PPS信号有随机误差，表现为1PPS信号上升沿相对于UTC时间有一定的抖动性，所以以1PPS信号为标准得到的相位误差值会受到影响，将原本1PPS信号的随机误差带入到测量的相位误差中，需要对得到的相位误差进行滤波处理。由1.2节GPS秒时钟误差分析知GPS秒时钟误差为随机误差，可以通过多次观察取平均值的方法滤除随机误差[1，5]。经实际验证，此方法简单有效，可以有效滤除GPS秒时钟随机误差对相位误差的影响。

2.1.3 分频电路

分频电路对本地晶振时钟进行分频，产生系统需要的高精度时钟。分频电路是一个分频可控的小数分频器，分频比需要根据经过滤波电路输出不断调节，实时消除晶振时钟误差。

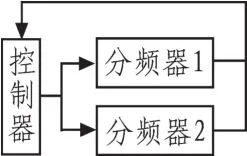
图2 小数分频原理框图Fig.2 Principle block diagram of decimal frequency divider

数字电路中不能直接实现小数分频，实际中是通过两个整数分频电路实现。控制器控制两个分频器，同一时刻只能有一个分频器工作，由控制器决定[6]。

设分频器1分频比为分频比的整数部分M，分频器2分频比为M+1。控制器的关键是如何控制分频器1和分频器2的分频次数，从而在较长的一段时间内是电路的平均分频比等于需要的小数分频比。设一段时间内，分频器1分频N1次，分频器2分频N2次，则这段时间内平均分频比为

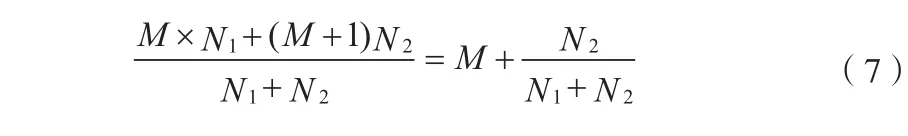
N1，N2取不同值时上式取值范围[M，M+1] ，理论上可以实现M值M+1间任意小数分频比。考虑到数字电路特点，在工程实现当中，将以上等式转化为

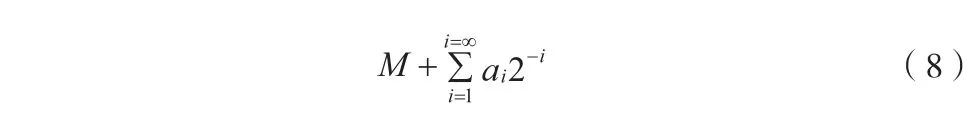
实现时i的取值不可能无限大，需根据系统允许的时钟误差值进行截取。

2.1.4 分频电路控制电路

有分频器原理分析知，分频电路有两个分频器F1和 F2，分频比分别为M和M+1。分频控制器的作用是产生控制信号，控制两个分频器的工作时间比例，使输出时钟在一段时间内的平均等效频率趋近于设置的时钟频率。

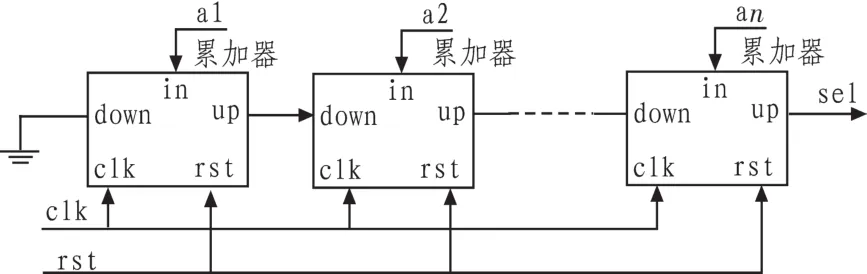
图3 分频控制器原理图Fig.3 Principle block diagram of frequency division controller

控制器是一个串行加法器，累加器位数由分频比的小数位决定。累加器输入值α1，α2，α3，…，αn的初始值为式（8）中的系数，考虑晶振频差范围和锁相环稳态误差，只有前几位系数可调，其他系数固定不变。电路正常工作时会依据鉴相结果进行小幅度调整。如果式（8）中的系数无穷或位数太大，需进行截断取舍。控制器输出一位控制信号sel，sel为高时选择分频器F2，为低时选择分频器F1。所以sel信号的占空比最终确定了分频电路的等效小数分频系数。

2.2 时钟误差分析及处理

2.2.1 输出时钟抖动性分析

通过以上方法，既可以消除晶振时钟的累积误差，同时通过滤波电路减小了GPS秒时钟随机误差对输出时钟的影响。

由于小数分频电路的具体结构，决定了以这种分频电路产生的分频时钟具有一定的抖动性[6]。对（8）式对应的控制器，分析他的固有抖动，令：

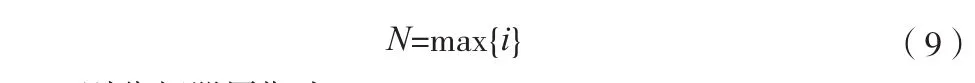
则分频器周期为：

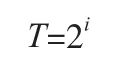
一个分频周期内分频器产生信号的抖动量为：

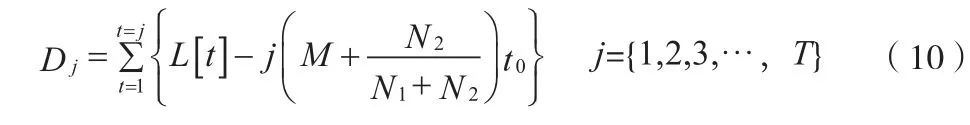
L[t]为控制器的控制信号，t0为晶振时钟的周期。则信号的抖动峰峰值为：

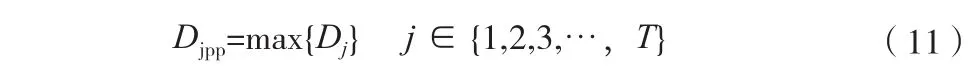
一个分频周期中的不同时刻，输出信号的抖动值都不同，每一个抖动值在一个周期内只出现一次，所以抖动频率为 1/T。

2.2.2 高精度时钟误差分析

晶振时钟频率误差和GPS秒时钟对高精度时钟的影响前面已经分析，数字锁相环电路能够对其进行补偿及平滑滤波处理。这里主要讨论由于分频电路小数部分截断误差对输出时钟的影响。当小数分频比位数进行截断处理后，输出时钟会在一个分频周期内有微小的频率误差。输出时钟再经过分频生成PPS时钟信号，与1PPS信号鉴频处理。输出时钟微小的频率差会体现为PPS信号与1PPS信号的相位误差，相位误差经滤波处理后，分频控制器会依据结果在下一个时钟周期对分频比的小数部分补偿，如此循环，结果表现为增加了输出时钟的抖动性，但不会有累计频率误差。

3 时钟驯服系统设计及技术实现

3.1 接收机工作状态确定

由于卫星信号可能受到各种不确定性因素的干扰，接收机工作状态可能会从正常状态进入不正常状态。接收机在不正常状态下，输出的秒时钟会有累积误差，此时时钟信号不可用；在正常工作状态下，输出的秒时钟累计误差趋于零，只有很小的随机误差，此时时钟可用。所以系统必须实时对接手机的工作状态进行评估，并根据接收机的不同工作状态调整时钟驯服电路。本文采用解析接收机导航数据的方式评估接收机工作状态。协议解析电路实时解析0183导航数据，并检测其中的定位模式位及数据有效位，如果定位模式为差分定位或自主定位且数据有效，认为接收机正常工作，否则认为接收机工作异常。

3.2 高精度同步时钟的实现原理

实现时，考虑到晶振频差的范围，电路增加了晶振频率检测模块，即对锁相环电路引入频率辅助电路，这样做好处是减小锁相环带宽，即提高输出时钟的稳定性又扩大了电路允许的晶振时钟误差范围[4]。系统开始后，等待晶振时钟稳定后，频率测量电路会在GPS秒时钟有效后连续256 s检测晶振频率，测量结果经平均滤波后作为晶振实际频率值，并对分频控制电路中的小数分频微调寄存器赋值。这样可以有效避免因为晶振频率偏差较大导致锁相环长时间未进入锁定状态。

时钟同步后，接收机工作正常时，根据本文提出的数字锁相环原理可以产生高精度的同步时钟。若接收机工作中卫星信号丢失，电路会保持最后一次分频比。

根据以上原理，本文设计完成了一个GPS高精度同步时钟电路，硬件原理如图4所示。

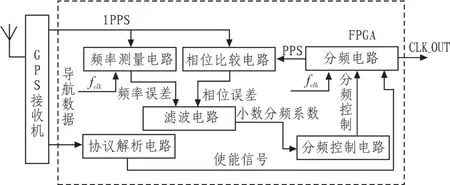
图4 GPS时钟驯服实现原理框图Fig.4 Principle block diagram of GPS clock taming

GPS接收接开始工作后，协议解析模块开始解析航数据，确定接收机的工作状况。当接收机捕获到4可以上卫星并输出有效时间信息后，驯服电路开始工作，输出经过驯服的时钟。

4 实际测试

依据以上原理设计电路，并对经过驯服的时钟进行实际验证测量。实现中接收机采用星际通GP5MX1513F1GPS，自主定位精度小于2 m，其妙时钟随机误差符合均值为0的正态分布，σ=20 ns 。晶振采用RAKON16.369M温补晶振，频率准确度1 PPM，频率稳定度0.5 PPM。输出32.768 K频率时钟。使用quartusII软件自带逻辑分析仪对时钟进行观察。图中CLK_32K信号为32.768 K输出时钟，PPS信号是CLK_32K时钟分频后得到的本地秒信号，PPS_1 Hz为卫星接收机输出的卫星秒时钟信号。valid信号为接收机时间信号是否有效的指示信号，为高表示信号有效，否则无效。采样时钟为16.369 M系统工作时钟，以卫星秒时钟PPS_1 Hz上升沿作为触发时刻。

从图5中知，系统输出时钟CLK_32K、本地秒信号PPS与卫星秒时钟PPS_1 Hz上升沿的对齐，即卫星信号有效时，本地秒时钟与卫星秒时钟同步，误差在61个纳秒以内（一个16.369M时钟周期）。

图6实验是将卫星秒时钟分成两路，在系统完成时间驯服后在FPGA内部强制给锁相环的卫星指示信号valid拉低，使驯服电路进入保持状态，经过一小时后的电路工作情况。

图5 卫星信号有效时信号时间关系Fig.5 Clock time relationship when satellite signals is valid

经多次试验验证，GPS信号失效一小时后最大误差在3个16.369M时钟周期内。通过本文设计的时钟驯服电路，很好的消除了晶振的累积误差并保持与卫星秒时钟的同步性。

图6 卫星信号无效时信号时间关系Fig.6 Clock time relationship when satellite signals is invalid

5 结束语

文中根据GPS秒时钟随机误差和温补晶振时钟累计误差互补的特性，依据数字锁相环原理，在FPGA中设计实现了一种使用GPS秒时钟测量温补晶振频率，实现高精度时钟的驯服电路。经实际测试，该设计产生高精度时钟不仅稳定度好，同步性高，而且实现过程简单。在GPS接收机失效后仍能较长时间的保持时钟的稳定性和同步性，能够很好地满足同步系统的要求。

[1] 李泽文，姚建刚，曾祥君，等.基于数字锁相环原理的GPS高精度同步时钟产生新方法[J].电力系统自动化，2009，32（18）：82-86.

LI Ze-wen，YAO Jian-gang，ZENG Xiang-jun，et al.New method of generating GPS high accuracy synchronous clock based on the digital phase-lock principle[J].Automation of Electric Power System，2009，32（18）：82-86.

[2] 徐文辉，王大为，黄鸿斌，等.实时在线式GPS授时系统原理与设计[J].哈尔滨工业大学学报，1998，30（5）：30-33.

XU Wen-hui，WANG Da-wei，HUANG Hong-bin，et al.Principle and design for real-time and on-line GPS giving time system[J].Journal of Harbin Institute of Technology，1998，30（5）：30-33.

[3] 魏丰，朱广伟，王瑞清，等.一种GPS校准的数字式高精度守时钟[J].仪器仪表学报，2011，32（4）：920-926.

WEI Feng，ZHU Guang-wei，WANG Rui-qing，et al.GPS Disciplind Precise digital timekeeping clock[J].Chinese Journal of Scientific Instrument，2011，32（4）：920-926.

[4] 胡华春，石玉.数字锁相环原理与应用[M].上海：上海科学技术出版社，1990.

[5] 黄翔，江道灼.GPS同步时钟的高精度守时方案[J].电力系统自动化，2010，34（18）：74-77.

HUANG Xiang，JIANG Dao-zhuo.A high accuracy time keeping scheme based on GPS[J].Automation of Electric Power System，2010，34（18）：74-77.

[6] 黄海生.一种可控分频比分频器的设计与研究[J].计算机工程与设计，2002，23（3）：8-10.

HUANG Hai-sheng.Research and design of a divider with controllable ratio[J].Computer Engineering And Design，2002，23（3）：8-10.

Design and implementation of GPS clock tame circuit based on FPGA

ZHANG Lei，HUANG Hai-sheng，ZHANG Bin
（Xi'an University of Posts and Telecommunications，Xi'an 710121，China ）

To meet the requirements of system for higsh precision clock，according to the characteristics of crystal clock without random error and the global positioning system（GPS）clock no accumulated error，this paper proposes a scheme of using GPS second signal to tame crystal oscillator clock to realize high precision clock.The scheme based on the principles of digital PLL frequency multiplier by measuring the phase error of the GPS seconds clock with the local clock to adjust the ratio of the clock divider circuit，real-time eliminating crystal clock cumulative error，So as to realize high precision system clock.Verified by practical，the method in the use of 16.369MHz temperature-compensation crystal oscillator，under the condition of GPS signals effectively the output clock error is less than 0.1ppm，GPS signal failure after 1 hour after the error is less than 0.3ppm.

GPS second clock；clock tame；high-accuracy clock；time synchronization；Field-Programmable Gate Array（FPGA）

TN492

A

1674-6236（2014）11-0061-04

2014-02-17 稿件编号：201402076

陕西省科技统筹创新工程计划战略基金资助项目（2012KTCQ01-06）；陕西省教育厅服务地方专项基金项目（2013JC10）

张 磊（1987—），男，陕西咸阳人，硕士研究生。研究方向：专用集成电路与系统集成。