交流电机调速系统中矢量控制技术的FPGA实现
徐茂盛 谷爱昱
(广东工业大学自动化学院,广东 广州 510006)
交流电机调速系统中矢量控制技术的FPGA实现
徐茂盛 谷爱昱
(广东工业大学自动化学院,广东 广州 510006)
在常见的电机控制系统中,空间矢量脉宽调制SVPWM是一种驱动电机旋转的高效脉冲调制方法。现介绍了矢量控制原理及其坐标变换,在此基础上构建了双闭环调速系统;同时介绍了SVPWM模块的FPGA生成方法,并对SVPWM模块在QuartusⅡ中进行了验证。该方案结合了SVPWM与FPGA的优点,在高性能运动控制系统中有重要的应用价值。
SVPWM;矢量控制;FPGA;运动控制系统
0 引言
随着电机技术的发展,电机在高动态性能调速领域的应用越来越广泛,对电机控制系统的要求也越来越高。常用的控制系统方案有矢量控制和直接转矩控制,而矢量控制系统具有可持续控制、调速范围宽等优点,使得矢量控制成为现代交流调速系统的重要控制手段之一。
基于转子磁场定向的矢量控制系统,通过由静止的ABC轴系到静止DQ轴系的变换实现三相到两相的“相数变换”,然后通过静止的DQ轴系到同步旋转MT轴系的变换实现“频率变换”,从而实现定子电流的2个分量ism和ist的解耦。经过坐标变换后的交流电机等效为他励的直流电机,从而可以用直流电机的控制手段方便地对交流电机进行控制。FPGA具有数字信号处理速度快和可在线设计、设计开发周期短的优势,在交流电机的控制领域有广阔的发展前景。
1 矢量控制的调速系统
交流异步电机的数学模型是一个高阶、非线性、强耦合的多变量系统,为了对电机实现矢量控制,需要将电机的数学模型进行坐标变换,简化电机的数学模型。
三相ABC轴系到两相静止DQ轴系的坐标变换:
(1)
式(1)是磁动势等效原则下得到的变换公式,通过变换实现了从静止ABC轴系到静止DQ轴系的三相到两相的“相数变换”。
静止DQ轴系到任意旋转MT轴系的变换:
(2)
同样式(2)是磁动势等效原则下得到的变换公式,通过由静止的DQ轴系到同步旋转MT轴系的变换实现“频率变换”。通过式(1)、式(2)的坐标变换实现了从三相对称正弦电流到两相对称正弦电流再到MT轴系两相绕组中的恒定直流电流的变换。经过坐标变换可以将电机的数学模型变换到任意旋转的MT轴系中,在经过添加M轴与转子磁链始终一致的约束条件即可实现fM与转子磁链同向,分量iM自然就是转子磁场的纯励磁分量,T轴分量就是纯转矩分量,从而实现转矩和励磁磁链的解耦。由于MT轴系是沿转子磁场定向的,常将这种矢量控制称为基于转子磁场定向的矢量控制,又称为转子磁场定向控制或者磁场定向控制。
矢量控制的基本方程:
电压方程:
(3)
式中,ωs为转自磁链矢量的电角速度;p为极对数;Lm为定、转子等效励磁电感;Ls为定子等效自感;Lr为转子等效自感;iM、iT为等效的定子电流在MT轴系下的电流分量;im、it为转子电流在MT轴系下的电流分量。
电流方程:
(4)
磁链方程:
(5)

转差频率:
(6)
由磁链方程(5)可得,转子磁链Ψr仅由iM产生,和iT无关,因而iM被称为定子电流的励磁分量。该式还表明Ψr与iM之间的传递函数是一阶惯性环节,其含义是:当励磁分量iM突变时,Ψr的变化要受到励磁惯性的阻扰,这和直流电机励磁绕组的惯性作用是一致的。再考虑式(4),更能看清楚励磁过程的物理意义。当定子电流励磁分量iM突变而引起Ψr变化时,当即在转子中感生转子电流励磁分量im,阻止Ψr的变化,使Ψr只能按时间常数Tr的指数规律变化。当Ψr达到稳态时,pφm=0,因而im=0,φm∝=Lmim,即φm的稳态值由im唯一决定。
2 矢量控制系统框图
本文采用速度闭环和电流闭环的双闭环转差频率控制系统(图1)。该方法基于矢量控制坐标变换实现磁场和转矩解耦控制的同时,避开了对旋转磁链幅值大小和相位的直接检测,而是应用稳态转差频率方程计算转差频率加上转子实际转动频率来获得转子磁场的位置。定子电流的转矩分量和励磁分量通过各自的PI控制调节输出,然后再通过坐标变换来控制SVPWM的脉宽调制。速度外环主要是采集转子速度信号,并与速度指令进行比较,为电流环提供电流给定设置值。通常为了防止电流过大,速度调节器需对电流输出进行限幅。电流环是通过采集u相和v相电流,并进行三相静止坐标到两相静止坐标和两相静止坐标到两相旋转坐标的变换,实现定子电流的解耦控制,分别得到用于产生磁场的励磁电流分量im和用于控制转矩的转矩电流分量it。将反馈得到的2个电流分量im和it分别与速度环中控制器得到的电流指令值im*和it*进行比较,经过PI调节器和坐标变换得到空间电压矢量。
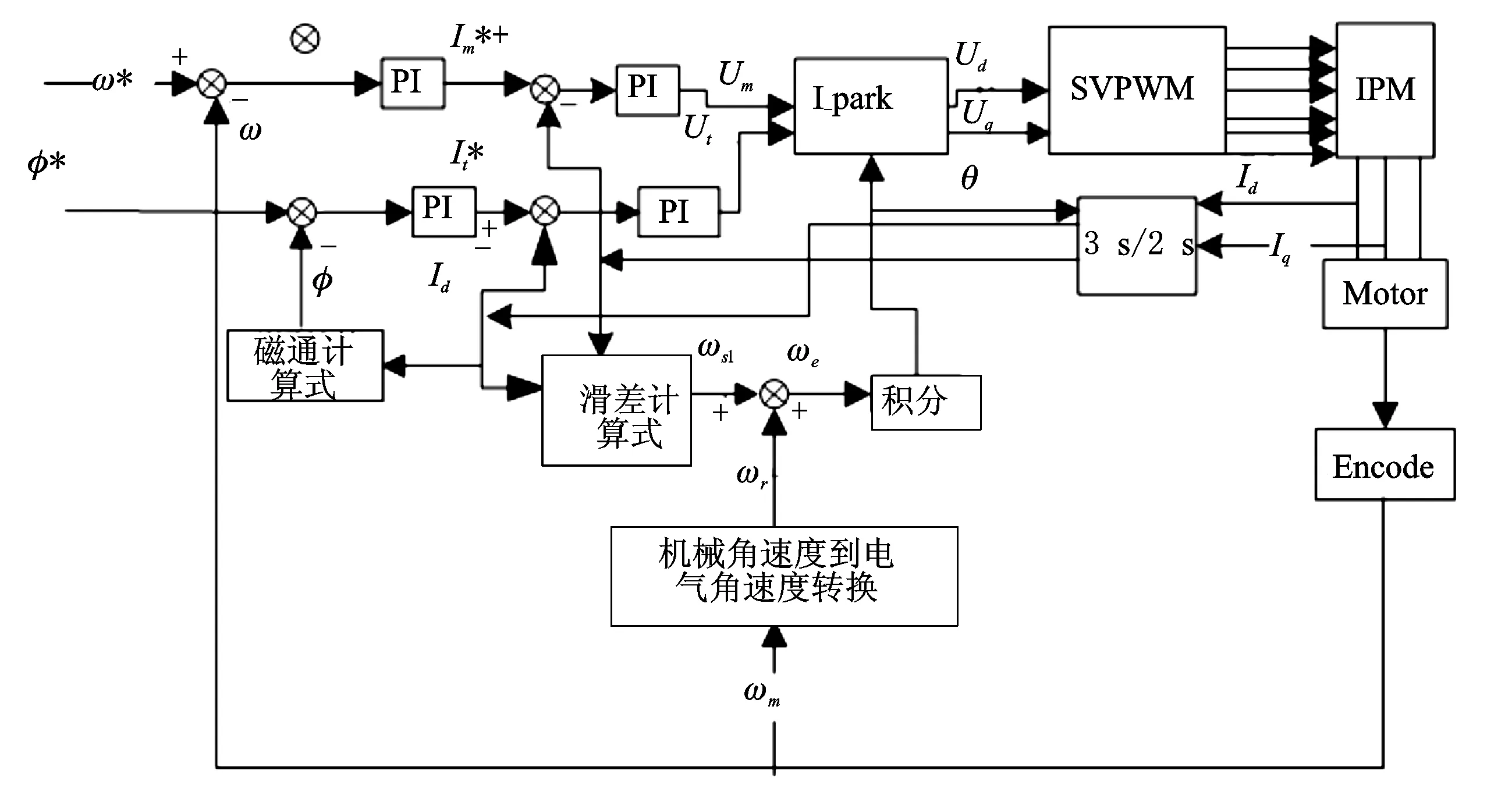
图1 交流电机双闭环矢量控制原理框图
3 系统整体的FPGA实现
对于系统整体的FPGA实现采用分模块的设计方法来实现。速度环电流模块包含脉冲倍频电路、转速及电气角度计算电路、正余弦查找表、PI调节器;电流环电路模块包含Clark变换、park变换、PI调节器、I_park变换、SVPWM产生模块等模块。Clark变换如上文式(1)所示,park变换如上文式(2)所示。I_park变换阵为:
(7)
式(7)中的θM是电气角度。对于以上几个模块均使用状态机的设计方法进行分模块设计,分别对每个模块在QuartusⅡ中进行编译和综合,最后调用Modelsim进行功能和时序仿真。本文重点介绍SVPWM生成模块。SVPWM生成原理图如图2所示。
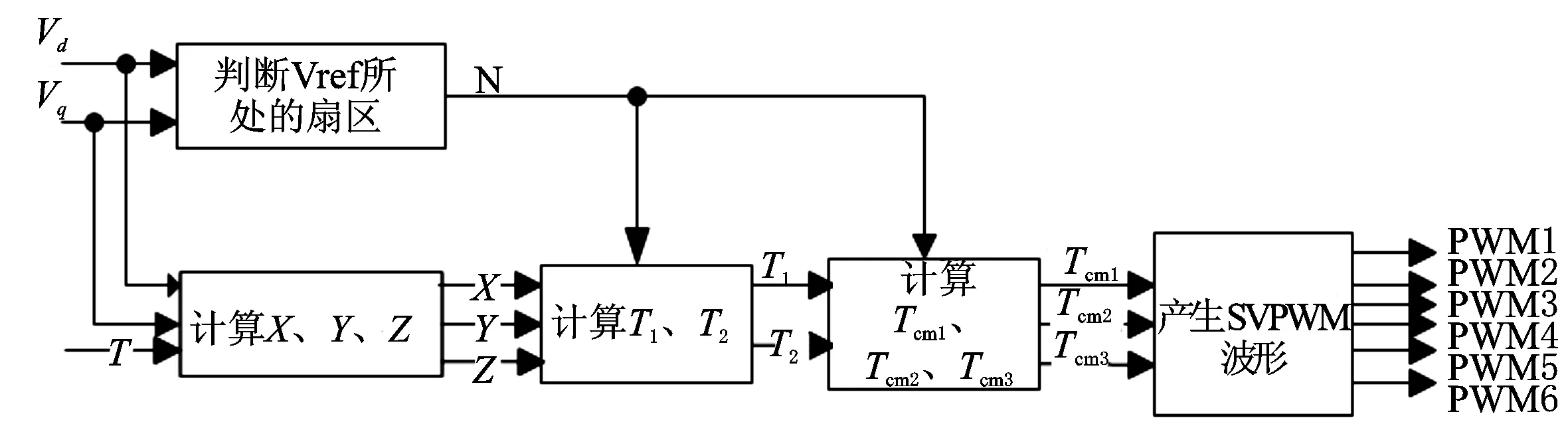
图2 SVPWM生成原理图
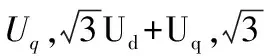
(8)
根据得到的X、Y、Z值,对应的扇区和导通时间的对应关系如表1所示。
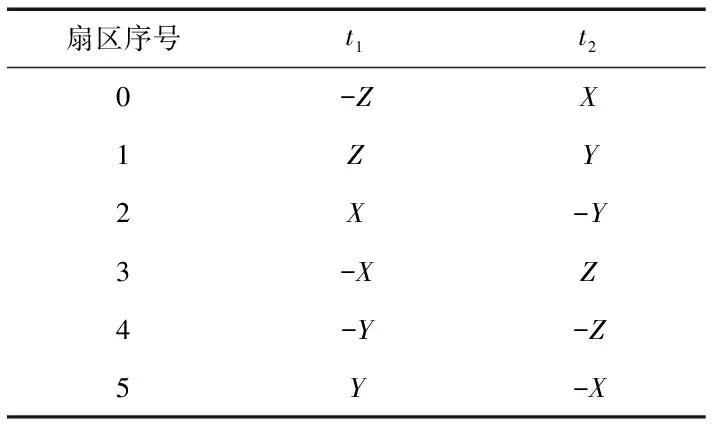
表1 导通时间和对应的扇区与X、Y、Z的对应关系
定义:
(9)
其中,Tpwm是一个开关周期。这样可以方便数字电路的实现并且可以将导通时间转化为用数字表达的占空比数据。不同扇区时PWM的占空比如表2所示。

表2 不同扇区时PWM的占空比
通过表2占空比的计算方法,得到了占空比实时变化的PWM波。PWM波通过三角载波与Tcm1、Tcm2、Tcm3的实时比较得到。
4 系统的仿真结果
将系统生成三路PWM接入RC滤波电路,滤除高频谐波,保留了低次谐波,其中包含基波和三次谐波,基波与三次谐波叠加变成马鞍波状。经过PWM调制后逆变电路输出的相电压必然包含相应的3倍频于正弦波信号的谐波,但在合成线电压时,各相电压中的这些谐波将互相抵消,从而使线电压仍为正弦波。
检测滤波之后的三路PWM信号,以此作为SVPWM模块功能的早期验证,经过试验验证,得到了3路互差120°的马鞍波形。
5 结语
本文主要介绍了矢量控制和SVPWM的生成。交流电机的矢量控制实现了定子电流的2个分量ism和ist的解耦,进一步实现了Te和Ψr的解耦,有利于对转速和磁链的控制。同时矢量控制采用连续控制,可获得较宽的调速范围。
另一方面,采用FPGA来实现控制系统,充分利用了FPGA响应速度快、开发周期短和设计灵活的优点,在电机的调速领域中有很大的应用价值。
[1]虞东海,颜钢锋.基于DSP的变频调速矢量控制系统[J].电气传动,2003(4)
[2]阮毅,陈伯时.电力拖动自动控制系统——运动控制系统[M].第4版.机械工业出版社,2010
[3]王成元,夏加宽,孙宜标.现代电机控制技术[M].机械工业出版社,2009
[4]潘松,黄继业.EDA技术实用教程:Verilog HDL版[M].第4版.科学出版社,2010
[5]常柯阳.基于FPGA的低功耗电机控制芯片的设计与研究[D].广东工业大学,2012
[6]周京华.CPLD/FPGA控制系统设计[M].机械工业出版社,2011
[7]解宏基.变频调速矢量控制交流三相异步电动机的仿真研究[D].大连海事大学,2000
2014-02-20
徐茂盛(1988—),男,河南人,硕士研究生,研究方向:控制理论与控制工程。
谷爱昱(1970—),女,河南人,副教授,硕士生导师,研究方向:电机与电器。

