一类图及其线图的Wiener指数

罗 宇， 王力工

(西北工业大学理学院应用数学系， 中国 西安 710072)

一类图及其线图的Wiener指数

罗 宇， 王力工

(西北工业大学理学院应用数学系， 中国 西安 710072)

Wiener指数W(G)是指一个连通图G中所有顶点对之间的距离之和.本文定义了一类具有圈数为r，围长为n的平面图Gr,s,t,n，证明了对于满足特定条件的正整数r,s,t,n，存在无穷个这样的图Gr,s,t,n，满足性质W(Gr,s,t,n)=W(L(Gr,s,t,n))，这里L(Gr,s,t,n)表示图Gr,s,t,n的线图， 推广了苏晓海等人的结果.

Wiener指数；线图；围长

设图G是一个具有顶点集V(G)={v1,v2,…,vn}和边集E(G)={e1,e2,…,em}的简单无向连通图.图G的顶点数n称为图G的阶数， 也记为n(G). 图G的线图L(G)是指它的顶点集V(L(G))=E(G),线图L(G)中两个互异的顶点相邻当且仅当在图G中相对应的两条边有一个公共顶点. 一个图G的圈数λ定义为λ(G)=m-n+1.

在本文中,作者的主要目标是找出满足下列等式的具有特定结构的图类，

W(L(G))=W(G) .

(1)

已知树的Wiener指数和其线图的Wiener指数总是不相等的[5]，对于单圈图，除了圈图Cn之外，均满足W(L(G)) g0)且圈数为2的平面非二部图满足等式(1). 在文献[14]中苏晓海等人分别研究了圈数r≥7的平面二部图和圈数r≥9的平面非二部图满足等式(1).在本文中，作者构造出了围长为n和圈数r的平面图Gr,s,t,n满足性质(1)，并证明了这样的图有无穷多个，推广了[14]的结果.

1 相关引理

为了便于计算图的Wiener指数，先介绍两个引理：

引理1[3]设G1和G2是任意两个图，v1∈V(G1)，v2∈V(G2)，且图G是将图G1的顶点v1和图G2的顶点v2重叠后得到的图，则图G的Wiener指数为：

W(G)=W(G1)+W(G2)+(n(G1)-1)dG2(v2)+(n(G2)-1)dG1(v1).

引理2[15]设a为正整数，则不定方程x2-y2=a有解的充分必要条件是a为奇数或4 的倍数.

2 主要结果

考虑如图1所示的图Gr,s,t,n，它的圈数为r，围长是n(n为正整数且n≥ 3)，图中的每个圈都是Cn，阶为nr+s+t+2，对于每一组正整数r,s,t和n，Gr,s,t,n都是简单平面图，其线图L(Gr,s,t,n)的具体结构见图1，其中它的完全子图中部分边没有画出.

定理1 图1中图Gr,s,t,n的Wiener指数为：

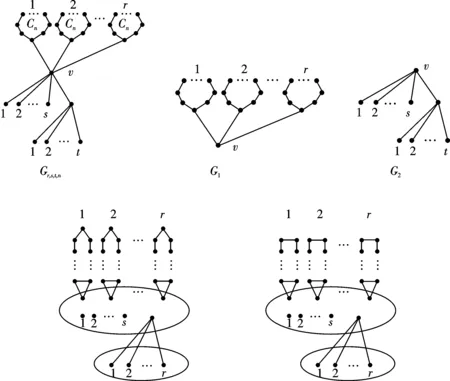
A.n=2k-1时，L(Gr,s,t,n) B.n=2k时，L(Gr,s,t,n)

(2)当n=2k时，W(Gr,s,t,n)=(2k3+4k2)r2+s2+t2+3st+(k2+4k)sr+(k2+6k)rt-(k3+2k2-6k)r+2s+2t+1.

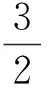
(2)当n=2k时，由Wiener指数的定义可得：W(G1)=(2k3+4k2)r2-(k3+3k2-2k)r,dG1(v)=(k2+2k)r,n(G1)=2kr+1,W(G2)=s2+t2+3st+2s+2t+1,dG2(v)=s+2t+1,n(G2)=s+t+2. 由引理1可得(2)成立．

定理2 图1中图Gr,s,t,n和L(Gr,s,t,n)，设ΔW(Gr,s,t,n)=W(L(Gr,s,t,n))-W(Gr,s,t,n)，则有：

定理3 对于图1中图Gr,s,t,n，当r,s,t,k,l均为正整数，且满足下列条件之一，则有ΔW(Gr,s,t,n)=0，即W(L(Gr,s,t,n))=W(Gr,s,t,n).

[2s+ 2t+ 2(k-3)r+ 3]2- 4k2r2=(8k2+28)r2-8sr-(8k2+28k+4)r+1.

引入任意正整数l，上式两边分别减去(8kl+4l2)r2，左边配方得

[2s+2t+2(k-3)r+3]2-[(2k+2l)r]2=(8k2-8kl-4l2+28)r2-8sr-(8k2+28k+4)r+1.

令x=2s+2t+2(k-3)r+3，y=(2k+2l)r，有

x2-y2=(8k2-8kl-4l2+28)r2-8sr-(8k2+28k+4)r+1.

显然上式等号右边是一个奇数，故x+y和x-y也是奇数，不妨令

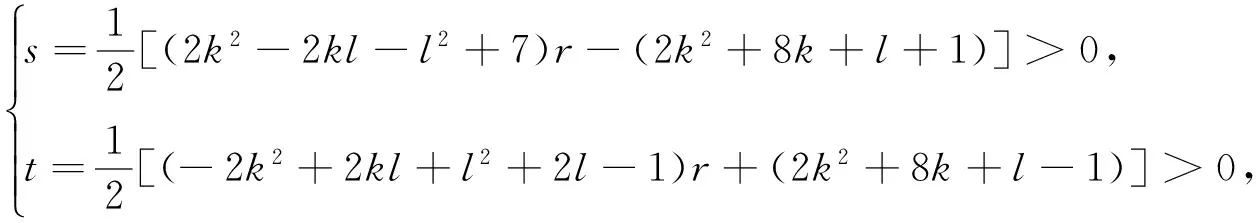
其中s+t+1=(l+3)r.于是定理3(1)的结果成立.

[2s+2t+2(k-2)r+3]2- 4k2r2=(8k2+8k+20)r2-8sr-(8k2+28k+4)r+1.

引入任意正整数l，上式两边分别减去(8kl+4l2)r2左边配方得到：

[2s+2t+2(k-2)r+3]2-[(2k+2l)r]2=[8k2-(8l-8)k-4l2+20]r2-8sr-(8k2+28k+20)r+1.

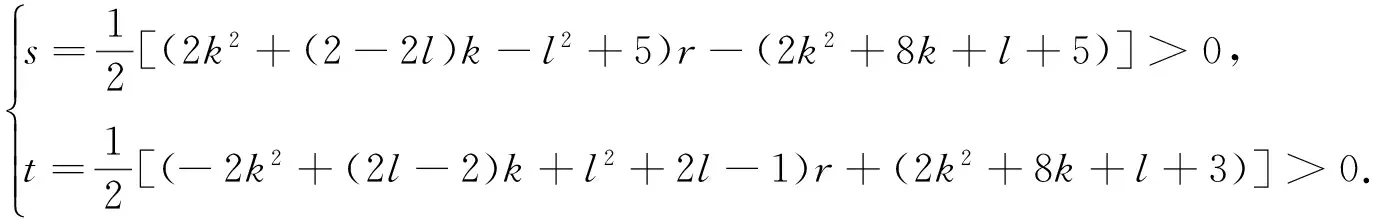
其中s+t+=(l+2)r.于是定理3(2)的结果成立.

推论1 当正整数n,k,r,s,t,l满足下列条件之一，W(L(Gr,s,t,n))=W(Gr,s,t,n)成立.

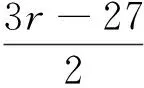
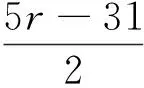
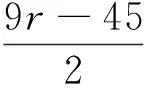
(4)n=6，k=3，l=2，s=r-25,t=4r+24,r≥25是整数；

(5)n=7，k=4，l=3，s=3r-34,t=3r+33,r≥12是整数；

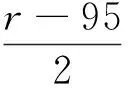
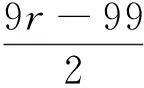
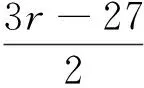
注当n=8，k=4 时，在0

[1] WIENER H. Structural determination of paraffin boiling points[J]. J Am Chem Soc, 1947，69(1)：17-20.

[2] DEVILLERS J, BALABAN A T. Topological indices and related descriptors in QSAR and QSPR[M]. Amsterdam: Gordon and Breach Science Publishers, 1999.

[3] DOBRYNIN A A, ENTRINGER R, GUTMAN I. Wiener index of trees: theory and applications[J].Acta Appl Math, 2001,66(3):211-249.

[4] BERTZ S H, WRIGHT W F. The graph theory approach to synthetic analysis: definition and application of molecular complexity and synthetic complexity[J]. Graph Theory Notes New York, 1998,35:32-48.

[5] BUCKLY F. Mean distance of line graphs[J]. Congr Numer, 1981,32(4):153-162.

[6] GUTMAN I. Distance of line graphs[J]. Graph Theory Notes New York, 1996,31:49-52.

[8] DOBRYNIN A A, GUTMAN I, JOVAEVIV. Bicyclic graphs and its line graphs with the same Wiener index[J]. Diskretn Analiz Issled Oper Ser 2, 1997,4(2):3-9(in Russian).

[9] 邓汉元. 一类化学图及其线图的Wiener指数[J]. 湖南师范大学自然科学学报， 2009,32(3):23-26.

[10] DOBRYNIN A A, MEL’NIKOV L S. Wiener index for graphs and their line graphs with arbitrary large cyclomatic numbers[J]. Appl Math Lett, 2005,18(3):307-312.

[11] DOBRYNIN A A, MEL’NIKOV L S. Wiener index, line graphs and the cyclomatic number[J].MATCH Commun Math Comput Chem, 2005,53(1):209-214.

[12] DOBRYNIN A A, MEL’NIKOV L S. Some results on the Wiener index of iterated line graphs[J].Electron Notes Discrete Math, 2005, 22:469-475.

[13] COHEN N, DIMITROV D, KRAKOVSKI R,etal. On Wiener index of graphs and their line graphs[J].MATCH Commun Math Comput Chem, 2010,64(3):683-698.

[14] 苏晓海，王力工. 两类图及其线图的Wiener指数[J]. 山西大学学报:自然科学版, 2011,34(3):397-401.

[15] 潘承洞，潘承彪. 初等数论[M]. 北京：北京大学出版社, 1994.

(编辑 沈小玲)

Wiener Index for a Class of Graphs and Their Line Graphs

LUOYu,WANGLi-gong*

(Department of Applied Mathematics, Northwestern Polytechnical University, Xi’an 710072, China)

The Wiener indexW(G) of a connected graphGis the sum of distances among all pairs of vertices ofG. A class of planar graphGr,s,t,nwith cyclomatic numberrand girthnis defined. It is proved that for given positive integersr,s,t,n, there are infinite families of graphsGr,s,t,nhaving the propertyW(Gr,s,t,n)=W(L(Gr,s,t,n)), whereL(Gr,s,t,n) is the line graph ofGr,s,t,n. These results generalize the results of Xiaohai Su et al.

Wiener index; line graph; girth

2012-11-21

国家自然科学基金资助项目(11171273)；国家级大学生创新创业训练计划资助项目(20120699107)

*

,E-maillgwangmath@163.com

O157.5

A

1000-2537(2014)01-0081-05