横向扰流条件下的喷射火脱火高度计算

蒋晓刚, 金良安,2, 迟 卫, 苑志江

(1.海军大连舰艇学院 航海系,辽宁 大连 116018)(2.中科院 大连化学物理研究所,辽宁 大连 116023)

横向扰流条件下的喷射火脱火高度计算

蒋晓刚1, 金良安1,2, 迟 卫1, 苑志江1

(1.海军大连舰艇学院 航海系,辽宁 大连 116018)(2.中科院 大连化学物理研究所,辽宁 大连 116023)

通过对Thornton模型的深入分析,以其风力影响下的火焰抬升高度计算公式为基础,得出了横向风力条件下的喷射火脱火高度计算模型,进而根据扰流和风力产生脱火的本质相同,利用火焰倾角这一关键参数将扰流速度转化为同等条件下的风速,最终建立了横向扰流条件下的脱火高度计算模型,并设计了同步数据采集实验平台对该模型进行检验及修正,结果表明:模型仿真结果与实验结果变化趋势相同,但在数值上存在一定差别;根据实验数据添加修正系数后,计算模型与实验结果符合良好;脱火发生后,随着横向扰流速度的增大,脱火高度逐渐增大并趋于平缓;相同条件下,扰流喷口半径越大,形成的脱火高度越大.另外实验发现,达到脱火条件时,火焰存在“腾跃”现象,即火焰瞬间脱离燃气喷口上升到一定高度.

喷射火; Thornton模型; 脱火高度; 横向扰流; 火焰倾角; 火焰长度

大量存在于油、气田以及工程管道、储罐和运输车船等多种场所的喷射火灾,由于其高发生率和强破坏性[1-2],历来是火灾扑救的重点和难点.基于工程燃烧中的脱火现象提出的脱火法施救技术[3]是为克服现有喷射火灾施救代价高、效率低、方法器材通用性差等固有问题[4]而提出的一种新型高效低耗通用技术,对其脱火高度变化规律地研究是该项技术最终得以工程化应用的重要基础.

然而,目前关于喷射火脱火高度的研究较少,大部分集中在由于燃烧不稳定,喷射火自发形成的脱火高度研究,例如,文献[5]中利用直径2.2mm的喷口对液化石油气射流扩散火焰进行了实验研究,实验结果表明：火焰脱开距离与燃料的释放速度成正比,并在此基础上提出了火焰脱开距离和流速口径比的半经验关系.文献[6]中利用边界层理论对氢气燃烧形成的火焰抬升模型进行了研究,得出了该条件下的计算模型并与其他模型进行了对比.另外,也有部分文献研究了风力影响下的火焰抬升高度,如Thornton模型基础上对单风向影响下的喷射火几何尺寸、火焰抬升高度等参数进行了研究[7];利用Shell模型的原理和计算方法,把喷射火焰视为近似倒立圆台形,构建了不同风向影响下的喷射火三维模型[8].

鉴于上述情况,为深入研究更为稳定高效的脱火技术,从而实现喷射火脱火法施救的工程应用,对扰流的脱火高度模型研究显得十分必要,为此文中以Thornton模型为基础,通过火焰倾角建立了横向扰流条件下脱火高度的计算模型,并设计了同步数据采集实验平台对其进行验证.

1 计算思想

1.1 脱火高度定义

脱火是指火焰脱离燃烧器喷口的一种不稳定的燃烧现象,脱火现象的产生由燃烧传播过程决定,其与燃料及氧化剂性质、燃烧器几何尺寸、混合物温度等都有一定关系[9].

大多数研究所涉及的脱火现象是由于自身燃烧不稳定形成的,其脱火高度指火焰底部到燃烧喷口的距离[10].文中主要研究的是扰流形成的脱火,现将其脱火高度定义为脱开火焰底部中心在燃料喷口轴线方向上的投影与燃料喷口中心的距离,如图1所示,其中b为脱火高度,α为火焰倾角,uw为风速,d为喷口直径.

图1 脱火高度示意Fig.1 Schematic diagram of liftoff height

1.2 Thornton模型分析

由于本研究是建立在Thornton模型基础之上,根据研究目的,首先对该模型中涉及的脱火高度计算公式进行研究,其风力影响下的脱火高度计算式为:

(1)

式中：Rw为风速uw与喷口速度uj的比值,Lb为风力影响下的火焰长度(m),K=0.185×e-20Rw+0.015,其余参数含义与图1相同.

火焰长度Lb的计算式为

Lb=L0×[(0.51×e-0.4uw+0.49)]×

[1.0-0.00607×(Θ-90°)]

(2)

式中:L0为静止火焰长度(m),L0=Y×Ds,其中Ds为燃烧等效直径(m);Ds=[4×Q/(π×ρ0×uj)]1/2;rj为燃气喷口半径(m);Q为燃气泄漏速率(kg/s);uj为喷口速度(m/s);ρ0为空气密度(kg/m3);Θ为孔口轴线与水平线的夹角(0°～90°).

Y通过解下列方程得到:

(3)

式(3)中:Ca，Cb和Cc为中间系数,g为重力加速度(m2/s),Wj为燃气摩尔质量(kg/mol).

火焰倾角α的计算式为:

(4)

经过对式(1～4)的分析发现,在燃料性质、喷口尺寸等因素确定的情况下,各个参数均是由喷口速度和风速决定,由此可知脱火高度主要与燃气喷口速度和风速有关.

1.3 具体思路

由于脱火形成的根本原因是可燃混合物速度大于燃烧速度,因此风力与扰流造成脱火的本质相同,如果能建立起风速和扰流速度之间的关系,即可通过Thornton模型中脱火高度的计算公式求解扰流条件下的喷射火脱火高度,因而文中需要解决的关键问题是建立两者速度之间的关系.

经过深入的分析发现,在风力和扰流条件下均会形成火焰倾角,并且其与两者速度都有直接关系,因此利用计算脱火高度的关键参数——火焰倾角α可对两者进行转换.具体思路为:令两者形成的火焰倾角相等,通过对公式的化简,统一含有的相同变量,将扰流速度转化为形成同等火焰倾角的风速,进而利用Thornton模型中横向风力影响下的脱火高度计算公式对横向扰流条件下的喷射火脱火高度进行计算.

2 模型建立

2.1 横向风脱火高度计算模型

鉴于横向扰流条件下的脱火高度计算模型是建立在Thornton模型基础之上,首先对该模型中横向风力条件下的脱火高度计算模型进行化简.

Lb=L0×[(0.51×e-0.4uw+0.49)]

(5)

而风力形成的火焰倾角计算式(4)可化简为：

(6)

根据射流火焰的运动规律[11],横向风力影响下的竖直喷射火形成的火焰倾角α应处于0°～90°之间,而α=0°意味着不附加外力自发形成脱火,不属于本文的研究内容.综述所述,与此向对应的横向风力影响下的脱火高度主体计算公式可化简为

(7)

将式(5～7)联立即是横向风力影响下的脱火高度计算模型.

2.2 横向扰流脱火高度计算模型

横向风脱火高度计算模型建立之后,即可根据文中计算思想建立同等火焰倾角条件下风速与扰流速度的关系,进而求得横向扰流脱火高度计算模型,因此需要明确两者各自的火焰倾角计算公式.

建立了横向风形成的火焰倾角计算公式,需要获得横向扰流形成的火焰倾角计算公式,该公式是建立在相交射流理论基础上,运用相交射流汇合流的运动方向计算公式推导得出,其计算式为[12]

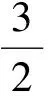
(8)

式中:θ为两射流夹角,由于求解的是横向扰流,故θ=π/2;Wj为燃气摩尔质量(kg/mol);Ww为扰流摩尔质量(kg/mol);rw为扰流喷口半径(m);rj为燃气喷口半径(m);vj为燃气出口速度(m/s),vw为扰流出口速度(m/s);ψ为动量修正系数,可根据半径比查图2得到.

图2 动量修正系数ψ与半径比rw/rj的关系Fig.2 Relationship between ψ and rw/rj

得出横向风和横向扰流形成的火焰倾角计算公式之后令两者相等,即α*=α,进而求出风速uw与扰流速度vw的关系.需要注意的是，求解时令两种情形的燃气出口速度保持一致,即vj=uj,并统一用uj表示.

由于式(6)分为两种情况,因此对其分别求解.首先求解Rw≤0.05的情形.此时,风力影响下的火焰倾角：

α=8000×Rw/Ri(Lb0)

(9)

式中:Rw=uw/uj,而将Ds，L0代入过渡参数Ri(Lb0)后,其可化简为：

(10)

将Rw和Ri(Lb0)代入式(9)化简后得出：

(11)

从而可将风速uw表示为：

(12)

由此可知,通过火焰倾角可将扰流速度vw转换为同等倾角下的风速uw,进而代入1.2节所述的脱火高度模型中对扰流形成的脱火高度进行求解.

同理求解Rw>0.05时的情形,此时

α=[134+1726×(Rω-0.026)1/2]/Ri(Lb0)

(13)

化简后得到：

(14)

联立式(8,14),可将此时风速表示为：

0.026uj

(15)

通过上述推导得出横向扰流速度vw和风速uw之间的转换关系为式(16).

(16)

通过式(16)即可将同等火焰倾角条件下的扰流速度转换为风速,进而可利用横向风条件下的脱火高度计算模型进行求解.

需要注意的是在具体的求解过程中还涉及到uw筛选的问题,这是由于在求解uw之前是分别假设Rw≤0.05或Rw>0.05,然而求出的解未必满足该条件,进而需要将所得结果带入Rw进行验证,如果符合当前假设条件,则uw与vw的转换关系成立,如果不符合,则需要更换假设条件重新计算.

通过上述分析推导,最终式(5～7，16)构成了横向扰流的脱火高度计算模型.

3 实验验证

3.1 实验装置

在Thornton模型基础上推导得出了横向扰流的脱火高度计算模型,为了验证模型的可靠性,特设计了人工扰流脱火同步数据采集实验平台,其主要由扰流系统、燃气系统和同步数据采集系统.扰流系统主要由扰流喷管、空气压缩机、流量计、导流管和可调阀门组成.燃气系统由燃气喷管、丁烷气瓶、可调导气喷头、导流管和玻璃转子流量计组成.同步数据采集系统由双摄像头和计算机组成.

为了对实验器材进行详细的说明,特绘制了实验装置示意图,如图3所示,其中丁烷和空气流量分别由空气玻璃转子流量计控制,流量计型号为北星LZB系列,流量计量程分别为16～160ml/min,100～1000ml/min,流量计精度为±4%.燃气成分为丁烷(纯度95%),扰流成分为空气.架设摄像头并连接计算机,将摄像头分别对准火焰产生位置和各个流量计,采用“摄像头—计算机”的方式进行取像,从而获得实验数据.燃料喷管竖直放置,扰流喷管水平放置,固定两者夹角为90°,两喷口底端均有进气孔与气源连接.实验时整套装置处于无外界气流扰动的相对封闭空间.

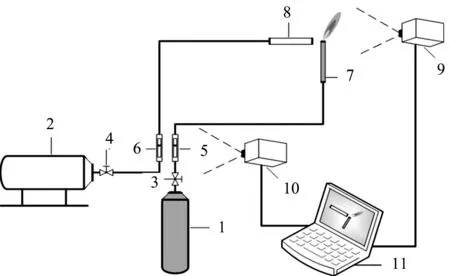
1-丁烷气瓶; 2-空气压缩机; 3、4-阀门; 5、6-流量计; 7- 燃气喷口; 8-扰流喷口; 9、10-摄像头; 11-计算机

3.2 实验数据与分析

为了检验与修正该模型,特设计了实验对其进行研究,实验主要内容为:固定燃气速度、燃气喷管直径以及两喷管夹角,改变横向扰流速度,研究不同喷管直径的脱火高度变化规律,进而验证脱火高度计算模型.

经过一系列的探索实验发现,燃气喷口较小时横向扰流较容易使得火焰脱开,并且当扰流喷口是燃气喷口的2倍以上时取得的脱火效果较好,因此将实验参数设置如下:燃气喷口半径rj=0.5mm,燃气出口速度uj=0.78m/s,两喷管夹角θ设定为90°,扰流喷口半径rw分别设定为1.0,1.5,2.0,2.5mm.其他参数为,重力加速度g=9.8m/s,常温条件下丁烷密度ρj=2.54 kg/m3,空气密度ρ0=1.21kg/m3,丁烷摩尔质量Wj=0.058kg/mol,空气摩尔质量Ww=0.029kg/mol,动量修正系数ψ可根据喷口半径比查图2获取.

在上述实验条件下,获得的不同喷管直径比脱火高度实验结果与计算结果如图4所示:

图4 不同扰流半径实验结果与计算结果比对Fig.4 Experiments and computation results withdifferent interfering jetflow radiuses

由图4可知,对于不同喷管直径比,计算结果与实验结果趋势相同,均是随着扰流速度增大,脱火高度逐渐增大并趋于平稳,但计算结果偏大,主要是由于Thornton模型在计算时假定喷射火形状为平截头圆锥形,与实际火焰有所不同,据此得出的计算结果会与实际情况存在偏差.

计算模型和实验结果的变化趋势相同表明该模型的正确性,但计算模型与实验结果存在一定偏差,因此需要利用实验结果对该模型进行修正.鉴于测量器材、实验条件等因素的影响,暂时无法确定具有通用性的修正系数,针对上述实验参数进行具体分析,经过多次实验与计算，最终将修正系数确定为0.8,对该模型进行修正,从而脱火高度计算模型变为：

(17)

将修正后的计算模型重新与实验结果比对,结果如图5所示:

图5 修正后计算模型与实验结果比对Fig.5 Results of modified model and experiments

从图5中可以看出,除了扰流喷管半径为1mm时脱火距离与修正后的计算模型差别较为明显,计算模型总体与实验结果吻合良好.

另外实验中发现,扰流速度较小(0～0.3m/s)时,火焰基本无法脱开,当速度持续增大时,脱火高度瞬间增大到一定数值,文中将这种现象称为“腾跃”,即火焰由于受到自身或外界因素影响发生脱火时火焰底部脱离燃烧喷口瞬间上升到一定高度的现象.之后随着扰流速度的增大,脱火高度会以较小的幅度持续增大并逐渐趋于平稳.

图6 不同扰流半径脱火高度修正模型计算结果Fig.6 Results of modified model with different radius

将不同扰流半径的脱火高度使用修正后的模型计算结果进行综合比较,如图6所示.

由图6可知,对于同一参数的喷射火,相同扰流速度下,随着扰流半径的增大,脱火高度逐渐增大.这主要是由于燃气喷口半径和出口速度固定后,其燃烧能力和燃烧稳定性便基本确定,扰流半径的增大使其干扰能力增大,从而脱火高度也有所增加.

另外实验发现扰流半径越大,最大脱火高度越趋于接近,并且其形成脱火高度的增大幅度逐渐减缓.分析认为,对于同样初始条件的燃烧,其脱火极限是一定的,也就意味着其最大脱火高度相同,因此扰流半径的增大并不能改变燃烧本身的最大脱火距离,从而形成了上述现象.

4 结 论

1)基于Thornton模型得出了横向风条件下的喷射火脱火高度计算模型,进而利用火焰倾角计算公式建立了同等条件下风速与扰流速度的关系,从而推导得出了横向扰流条件下的喷射火脱火高度计算模型.

2)设计实验对推导得出的模型进行了验证,模型仿真结果与实验结果变化趋势相同,均是随着扰流速度的增大,脱火高度逐渐增大并趋于平稳,但计算数值偏大,后经多次实验与计算结果比对,最终添加了修正系数对模型进行了修正,修正后的模型与实验结果符合较好.

3)对于同一参数的喷射火,相同扰流速度下扰流喷口半径的增大能够增加脱火高度,但是最大脱火高度趋于接近,表明燃烧自身参数确定后,其最大脱火高度一定.

4)实验中发现,当喷射火发生脱火的瞬间,火焰会迅速脱离燃气喷口“腾跃”到一定高度,进而脱火高度再随着扰流速度的增大而逐渐增大.

References)

[1] 马磊, 李永树. 城市天然气管网预警系统的研究与实现[J]. 中国安全科学学报, 2010, 20(9): 171-172. Ma Lei, Li Yongshu. Research and realization of urban natural gas pipeline network pre-warning system[J].ChinaSafetyScienceJournal, 2010, 20(9):171-172.(in Chinese)

[2] 苏石川, 王乐, 王亮，等. 某散货船机舱火灾的数值计算与分析[J]. 江苏科技大学学报:自然科学版, 2011, 25(2): 144-148. Su Shichuan, Wang Le, Wang Liang, et al. Numerical calculation and analysis of fire disaster in bulk engine room[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2011, 25(2): 144-148.

[3] 迟卫, 罗育洪, 蒋晓刚，等. 喷射火灾脱火法施救的实验研究[J]. 消防科学与技术, 2011, 30(2): 151-155. Chi Wei, Luo yuhong, Jiang xiaogang, et al. Experimental study against jet fire based on lift-off fire[J].FireScienceandTechnology,2011, 30(2): 151-155.(in Chinese)

[4] 罗育洪, 迟卫, 谢田华,等. 喷射火灾现有施救方法的主要问题及对策[J]. 海军大连舰艇学院学报, 2010, 33(5): 80-83. Luo Yuhong, Chi Wei, Xie Tianhua,et al. Disadvantages and countermeasures of extinguishing methods for jet fire[J].JournalofDalianNavalAcademy,2010, 33(5): 80-83.(in Chinese)

[5] Kiran D Y, Mishra D P. Experimental stydies of flame stability and emission characteristics of simple LPG jet diffusion flame[J].Fuel, 2007, (86):1545-1551.

[6] Onokpe O,Cumber P S.Modelling lifted hydrogen jet fires using the boundary layer equations[J].AppliedThermalEngineering,2009, (29):1383-1390.

[7] 王兆芹, 冯文兴, 程五一. 高压输气管道喷射火几何尺寸和危险半径的研究[J]. 安全与环境工程, 2009, 16(5):108-110. Wang Zhaoqin, Feng Wenxing, Cheng Wuyi. Analysis of geometry and hazardous radius of jet flame from high-pressure natural gas pipeline[J].SafetyandEnvironmentalEngineering,2009, 16(5):108-110.(in Chinese)

[8] 陈文江, 陈国华. 基于虚拟现实技术的喷射火事故三维动态仿真及应用[J]. 中国安全科学学报, 2009, 19(3):32-38. Chen wenjiang, Chen guohua. The three-dimensional dynamic simulation of jet fire based on virtual reality technology and its application[J].ChinaSafetyScienceJournal,2009, 19(3):32-38.(in Chinese)

[9] 徐通模. 燃烧学[M]. 北京: 中国机械出版社, 2010:88-91.

[10] Palacios A,Casal J.Assessment of the shape of vertical jet fires[J].Fuel,2011, 90:824-833.

[11] 董志勇. 射流力学[M]. 北京: 科学出版社, 2005: 7-10.

[12] 蒋晓刚, 金良安, 迟卫,等. 人工扰流条件下喷射火焰的倾角计算[J]. 消防科学与技术, 2011, 39(11): 987-990. Jiang Xiaogang, Jin Liang′an, Chi Wei, et al.Calculative method for oblique angle of ejecting flame interfered by man-made jet flow[J].FireScienceandTechnology,2011, 39(11): 987-990.(in Chinese)

(责任编辑：贡洪殿)

Calculationofliftoffheightofjetfirecausedbytransverseinterferingjetflow

Jiang Xiaogang1, Jin Liang′an1,2, Chi Wei1, Yuan Zhijiang1

(1. Department of Navigation, Dalian Naval Academy, Dalian 116018, China)(2. Dalian Institute of Chemical Physics, Chinese Academy of Science, Dalian 116023,China)

Based on the Thornton model, the expressions for liftoff height of jet fire caused by wind were analyzed. Then, the liftoff height model of jet fire under the effect of transverse wind was built. Because interfering jetflow and wind were essentially the same for fire liftoff, the relationship between interfering jetflow velocity and wind velocity was obtained through flame oblique angle. Finally, the liftoff height model of jet fire under the effect of transverse interfering jetflow was built. And the synchronous data acquisition experiment device was designed to verify and modify the model. The results show that the change trend of simulation and experiment results are the same, but the numerical values have a little difference. When the correction factor is added to the model, the simulation results accord with the experiments. With the augment of transverse interfering jetflow velocity, the liftoff height increases gradually and then flattens out. Under the same condition, the liftoff height increases with the radius of interfering jetflow nozzle. In addition, the experiments find that the fire has a prance phenomenon at the moment of fire lift off, which means that the fire breaks away from the spout of gas instantly.

jet fire; Thornton model; fire liftoff height; transverse interfering jetflow; flame oblique angle; flame length

10.3969/j.issn.1673-4807.2014.04.011

2014-04-22

蒋晓刚(1988—)，男，博士研究生，研究方向为火灾施救与防护.E-mail:i.music@163.com

TK121; X913.4

A

1673-4807(2014)04-0358-06