Relationship between Phase Coexistence and Properties inPiezoelectric Materials

YAO Yonggang, ZHOU Chao, XUE Dezhen, YANG Yaodong, REN Xiaobing

(Multi-Disciplinary Materials Research Center, Frontier Institute of Science and Technology,Xi′an Jiaotong University, Xi′an 710054, China)

1 Introduction

With the rising environmental and human health concerns by using toxic Pb in industrial and commercial devices, people are looking for sustainable and environmental friendly Pb-free materials[1]. Intensive works have contributed to Pb-free piezoelectric research, but few reported Pb-free materials can actually compete with Pb family[2-5]. A guideline for developing high performance piezoelectrics becomes essentially important.

In 2000, Fu and Cohen proposed that the giant piezoelectric response can be induced by intrinsic polarization rotation mechanism by first principle calculation[6]. Experimentally, Noheda et al found a narrow intermediate phase between T and R phase in Pb-based high performance piezoelectric systems, which serviced as a bridge phase facilitating the polarization rotation from T[100] to R[111][7-10]. More recently, the contribution of polarization extension from ferroelectric to paraelectric phase was proposed by Damjanovic et al as another important factor[11-13]. Thus, easy polarization extension and rotation mechanism (low energy barriers for polarization variation) have been accepted as the two most important intrinsic factors contributing to the materials′ permittivity and piezoelectricity (theseacproperties) enhancement.

However, this mechanism is largely relying on a free energy analysis, which is hard to apply in a material design directly. How to link this free energy mechanism with real applications such as designing high performance piezoelectrics? Is it possible to convert free energy analysis into a simpler materials design guideline? All in all, a simple, clear and operable mechanism is needed.

On the other hand, from experiment, it is found that the highacproperties in Pb-based piezoelectrics are really related to a morphotropic phase boundary (MPB), a phase transition boundary formed by composition change[14-16]. Recently, Liu and Ren[17]found that the high performance at MPB actually originates from a triple point with three phases (e.g., Cubic-Tetragonal-Rhombohedra, C-T-R) coexisted. Based on this idea, at least three new Pb-free triple point type MPB systems have been discovered and their piezoelectricity are as high as 450-600pC/N[18-20]. Higher piezoelectricity and permittivity have been reported in the Pb-free BaTiO3-xBaSnO3system at its quasi-quadruple point, a point in the phase diagram with nearly four phases coexisted[21].

Although these materials still have some drawbacks, such as the Curie temperature (Tc) is too low to use in our daily life, these experimental results do give us a hint that the ferroelectric material′s ac properties are highly depended on its phase coexistence state. Obviously, such relationship can be used as a simple guideline to develop high performance piezoelectric materials if it can be clarified. However, a comprehensive study and details of this relationship are still not clear.

This work clarifies the property and phase coexistence relationship from both theoretical and experimental aspects, will give an important guidance to find a high piezoelectric Pb-free material by different phase-coexistence approach. Phase coexistence analysis method may be a right and simple way to reveal the polarization rotation and extension mechanism and rebuild the structure-property relationship.

2 Method

In order to reveal the difference between these phase coexistence states, free energy of different phase coexistence states was calculated by Landau theory. Different energy barriers for polarization rotation and extension for different coexistence states can be found, and their abilities for property enhancement can be revealed too.

To analyze all four common phases in ferroelectrics: Cubic, Tetragonal, Orthorhombic, Rhombohedra (C, T, O, R), 6th order Landau-Devonshire model is used, the lowest order to have all these four phases[22-23]. The equation is as follow[14, 18, 21, 24-28]:

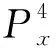
(1)

WhereFmeans the free energy of the system;F0is the free energy of the paraelectric phase;Pis the order parameter-polarization, anda,b,care the fitting parameters. This equation means the free energy of the system can be expanded to the polynomial expression of the order parameter polarization.

At a phase coexistence state, the free energy of coexisted phases should be equal; also, the first deviation of free energy for these phases should equal to zero to make the phase stable. Take quadruple point with C-T-O-R coexistence as an example:

phase coexistence:

(1)

phase equilibrium:

(2)

For simplicity, define ‖PT‖=‖PO‖=‖PR‖=P0, which means the polarizations in different ferroelectric phases have the same length, but different orientations. Our model only concerns up to 6thorder polarizations with the condition of same polarization length for different ferroelectric phases. This gives essential simplicity for us to see the difference between these phase coexistence states while keeps the result similar. For example, sequence of the ability for property enhancement. However, one should notice that this raises the issue of totally isotropic polarization rotation energy profile for C-T-O-R and T-O-R states, which (in reality) should be very low anisotropy states if higher order polarization terms or different length polarization are considered.

3 Results

3.1 Calculated result

Here we summarized the calculated results in Table 1. (NearTccoexistence states: C-T-O-R, C-T-O, C-T; belowTccoexistence states: T-O-R, T-O, T) For these free energy equations, they are composed of three components: i)F0, energy of paraelectric phase, same for every equations; ii) 2-4-6 order isotropic term (underlined with single line), function ofP, the sphere energy; iii) 2-4-6 anisotropy term (underlined with double line), function of [Px,Py,Pz], the anisotropy energy. In this way, every state or its equation can be divided into three parts: the basic energyF0, the isotropic term and the anisotropy term.

For property enhancement, it is not the free energy itself but the energy barriers for polarization variation that matters. From free energy view, great property enhancement comes from easy polarization variation, namely low energy barriers for polarization variation. To analyses the polarization variation energy barriers, each polarization variation can be decomposed into two components: variation in its direction and length. The former is polarization rotation, namely polarization variation in its directions but with constant length; the latter is polarization extension, namely polarization variation in its length but in one direction. Energy barriers for polarization rotation only come from the anisotropy term because polarization rotation doesn′t affect the isotropic term at all; while energy barriers for polarization extension mainly come from the scale of the isotropic term, if the anisotropy term is fixed.

Table1 The calculated results of different phase coexistence states. Single line for the isotropic term, double line for the anisotropy term

To simply conclude, coexistence of several ferroelectric phases can lower the polarization rotation barriers, and thus facilitate polarization rotation enhancement for ac properties; coexisted with Cubic phase can significantly lower the polarization extension barriers, and thus facilitate the polarization extension enhancement for ac properties.

3.2 Schematic free energy profiles

In order to show the difference between these free energy equations clearly, schematic energy landscapes of different situations were showed in Fig.1 and Fig.2. The values of the parameters are chosen according to the relations listed above.

Since the enhancements ofacproperties usually come from the easy polarization rotation and extension, we analyses the free energy behavior from these two aspects. For polarization rotation case, free energy profile for polarizations of ‖P‖=P0were showing in Figure 1 in 3D view. For polarization extension case, the free energy value for polarizations in directions of T[001], R[111], O[011], were showing in Figure 2.

From these figures, the rules stated in the equation parts can be also found. From polarization rotation case Fig.1, it is quite clear that coexisted with the same ferroelectric phases gives out similar anisotropy energy barriers for polarization rotation barriers, which is clear in comparison of the upper figures with the lower ones; states with coexistence of several ferroelectric phases have much flatter energy profiles and low energy barriers, and can facilitate polarization rotation process, which is clear by comparing from left to right. For polarization extension case Fig.2, those states coexisting with C phase have very low energy barriers for polarization variation from a ferro to a para phase, and can facilitate the polarization extension process, which is clear from the comparison of upper figures with the lower ones.

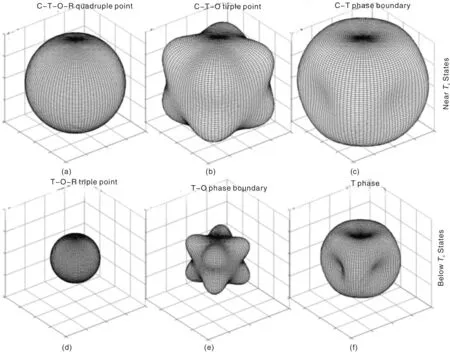
Fig.1 Free energy landscapes for polarization rotation case. Near Tc states: (a) C-T-O-R quadruple point[21], (b) C-T-O triple point, and (c) C-T phase boundary[21]. Below Tc states: (d) T-O-R triple point, (e) T-O phase boundary[21], and (f) T phase only

Fig.2 Free energy landscapes for polarization extension case. Near Tc states: (a) C-T-O-R quadruple point[21], (b) C-T-O triple point, and (c) C-T phase boundary[21]. Below Tc states: (d) T-O-R triple point, (e) T-O phase boundary[21], and (f) T phase only

In this way, different phase coexistence states have been successfully related to a certain free energy profile. Further, difference profiles and energy barriers certainly indicate different performances. So what about the experiments?

3.3 Experimental proofs

Based on the polarization rotation and extension mechanism, different property enhancements can be expected because of different energy barriers for different phase coexistence states. For example, quadruple point may give the largest enhancement due to no energy barrier for polarization rotation and lowest energy barrier for polarization extension; with less ferroelectric phases exist together, the polarization rotation energy barrier becomes larger; and without a C phase, there is a large energy barrier for polarization extension, thus a decrease inacproperties.

Below are the experimental measurements of different phase coexistence situations (Fig.3). These systems are carefully chosen to eliminate the effect of system difference. They are BaSnO3doped BaTiO3(as BT-xBS, Fig.3a)[21], Ba(Sn0.12Ti0.88)O3doped (Ba0.7Ca0.3)TiO3(as BST-xBCT, Fig.3b)[19], and CaTiO3doped BaTiO3(as BT-xCT, Fig.3c). These three systems are all BaTiO3based systems with similar dopants; and they show almost all the phase coexistence situations. These facts make these three systems excellent for ac properties comparison and can yield reasonable results. Fig. 3a, 3b, and 3c show the different phase diagrams composed by BT, CT, and BS: quadruple point C-T-O-R and double MPB T-O and O-R in BT-xBS; triple point C-T-R and MPB T-R in BST-xBCT; phase boundary C-T, T-O, and O-R in BT-xCT. Because permittivity is much sensitive nearTc, while piezoelectricity is only sustainable belowTc, so, we choose to compare the permittivity value atTcfor nearTcstates (Fig 3d, 3e, and 3f), and the piezoelectricity coefficientd33at room temperature (RT) for far belowTcstates (Fig.3g, 3h, and 3i).

For nearTccases, permittivity at C-T-O-R quadruple point and C-T-R triple point reach a large value while no big different in C-T phase boundary case. Clearly, compared with C-T or C-R phase boundaries, quadruple and triple points have a large enhancement on its permittivity. Also, the permittivity at quadruple point is even larger than that at triple point, indicating the enhancement at quadruple point is even larger. For belowTccases, the phase boundaries T-O and O-R in BT-xBS system and phase boundary T-R in BST-xBCT system have the peakd33value in each system, whiled33decreases slightly for single phase T in BT-xCT system with increase dopants. This indicates phase boundary can enhance the piezoelectric properties, which has been known for long time.

Fig.3 experimental data for different phase coexistence states: (a), (b), (c) phase diagram; (d), (e), (f) permittivity at Tc (near Tc properties); (g), (h), (i) d33 at RT (below Tc properties) for BT-xBS, BST-xBCT, and BT-xCT system (Partial data are cited from ref[21] and ref[19])

These experimental results satisfy our calculated results very well, indicating that phase coexistence states do have such a relationship with property enhancement, and this relationship can be well understood by free energy analysis from polarization rotation and extension aspects.

3.4 T-O-R phase coexisting

From our calculated result, a T-O-R phase coexistence should possess piezoelectricity much larger than that of a single phase boundary because it′s an isotropic state for polarization rotation. Although clear and direct declaration for a T-O-R coexistence state were not found in previous literature yet, indirect evidences such as Pb-based high performance PZT[9], PZN-PT[29], PMN-PT[7]can support this finding. They all have a very narrow intermediate phase between T and R phase and greatacproperties in this region were found and attributed to the easy polarization rotation from T[100] to R[111] facilitated by this intermediate phase (lower energy barrier for polarization because of this intermediate phase)[10, 30].

It found[12, 31]that it is not the intermediate phase itself giving large enhancement to the properties, but the narrowness of this intermediate phase really matters. It showed that a narrow intermediate phase, mimicking but not a truly T-O-R coexisting state, can largely enhance theacproperties.

This may be a new clue to search for high performance piezoelectric ceramic systems by narrowing the intermediate phase between two ferroelectric phases, to mimic a triple phase coexistence state, which is highly possible by modifying BaTiO3or KNbO3, who has a T to O to R ferroelectric transition sequence originally. High performance piezoelectrics[32-33]found in these two systems support our opinion.

3.5 Relationship

To summarize above results, a relationship diagram of ac properties at different phase coexistence situations can be drawn out (see Figure 4a): the less ferroelectric phases coexisting (FE loss), the harder for polarization rotation and ac properties decrease; without a C phase (PE loss), a large energy barrier will limit polarization extension andacproperties drop too.

Fig.4 (a) schematic diagram of the relationship between material′s ac properties with its different phase coexistence states and (b) experimental d33 distribution in BT-xBS system (PB: phase boundaries, QP: quadruple point C-T-O-R, modified from ref[21])

An experimental proof to reveal this relationship can be found in Fig.4b, showing the distribution of piezoelectric coefficientd33(color contour map, cited and modified from ref[21]) with relation to its phase coexistence state in BT-xBS system. From this figure, the piezoelectricity of different phase coexistence states can be clearly revealed and compared, which shows a phase status dependence of piezoelectric performance, and this dependence fits well to the relationship we summarized above.

Knowing this relationship in mind, it helps when one tries to design a high performance piezoelectric system or predict the piezoelectricity distribution by its phase diagram. To get high performance, it is better that people can acquire a more-phases coexistence state, which will give largest additional enhancement on the basis of materials′ own performance. This can be achieved by doping elements with different phase transition sequence or simply by strain engineering. Also, the phase diagram becomes even more important to predict the performance of the system according to its phase coexistence states.

4 Conclusion

The relationship between phase coexistence state and its properties has been built via free energy analysis. This work concretes the polarization rotation and extension mechanism into a material design view. It may simplify the process of developing high performance piezoelectric materials by searching, or engineering a phase coexistence state. Regarding the similarity between different ferroic materials, one can expect this “phase coexistence and properties” idea also can be applied to the ferromagnetic and ferroelastic fields to seek better materials.

[1] Cross E. Materials Science: Lead-Free at Last[J].Nature, 2004, 432(7 013): 24-25.

[2] Zhang S,etal. Lead-Free Piezoelectric Ceramics vs. PZT?[J].JElectroceram, 2007， 19(4): 251-257.

[3] Panda P. Review: Environmental Friendly Lead-Free Piezoelectric Materials[J].JMaterSci, 2009， 44(19): 5 049-5 062.

[4] Rödel J,etal. Perspective on the Development of Lead-Free Piezoceramics[J].JAmCeramSoc, 2009， 92(6): 1 153-1 177.

[5] Takenaka T,etal. Current Developments and Prospective of Lead-Free Piezoelectric Ceramics[J].JpnJApplPhys, 2008, 47(5): 3 787-3 801.

[6] Fu H， Cohen R. Polarization Rotation Mechanism for Ultrahigh Electromechanical Response in Single-Crystal Piezoelectrics[J].Nature, 2000， 403(6 767): 281.

[7] Noheda B,etal. Phase Diagram of the Ferroelectric Relaxor (1-x)PbMg_{1/3}Nb_{2/3}O_{3}-xPbTiO_{3}[J].PhysRevB, 2002， 66(5): 054 104.

[8] Noheda B,etal. Polarization Rotation via a Monoclinic Phase in the Piezoelectric 92% PbZn_{1/3}Nb_{2/3}O_{3}-8% PbTiO_{3}[J].PhysRevLett, 2001, 86(17): 3 891-3 894.

[9] Noheda B,etal. A Monoclinic Ferroelectric Phase in the Pb (ZrTi) O Solid Solution[J].ApplPhysLett, 1999, 74: 2 059.

[10] Guo R,etal. Origin of the High Piezoelectric Response in PbZr_{1-x}Ti_{x}O_{3}[J].PhysRevLett, 2000, 84(23): 5 423-5 426.

[11] Damjanovic D. Contributions to the Piezoelectric Effect in Ferroelectric Single Crystals and Ceramics[J].JAmCeramSoc, 2005, 88(10): 2 663-2 676.

[12] Damjanovic D. A Morphotropic Phase Boundary System Based on Polarization Rotation and Polarization Extension[J].ApplPhysLett, 2010, 97(6): 062 906.

[13] Damjanovic D. Comments on Origins of Enhanced Piezoelectric Properties in Ferroelectrics[J].Ultrasonics,FerroelectricsandFrequencyControl,IEEETransactionson, 2009, 56(8): 1 574-1 585.

[14] Carl K, Härdtl K H. On the Origin of the Maximum in the Electromechanical Activity in Pb(ZrxTi1-x)O3Ceramies near the Morphotropic Phase Boundary[J].PhysicaStatusSolidiA, 1971, 8(1): 87-98.

[15] Jaffe B,etal. Piezoelectric Properties of Lead Zirconate-Lead Titanate Solid-Solution Ceramics[J].JApplPhys, 1954, 25: 809.

[16] Jaffe B,etal.PiezoelectricCeramics[M]. London: Academic Press, 1971.

[17] Liu W, Ren X. Large Piezoelectric Effect in Pb-Free Ceramics[J].PhysRevLett, 2009, 103(25): 257 602.

[18] Zhou C,etal. Triple-Point-Type Morphotropic Phase Boundary Based Large Piezoelectric Pb-Free Material-Ba(Ti[sub 0.8]Hf[sub 0.2])O[sub 3]-(Ba[sub 0.7]Ca[sub 0.3])TiO[sub 3][J].ApplPhysLett, 2012， 100(22): 222 910.

[19] Xue D,etal. Large Piezoelectric Effect in Pb-Free Ba (Ti, Sn) O3-x(Ba, Ca) TiO3Ceramics[J].ApplPhysLett, 2011， 99: 122 901.

[20] Bao H,etal. A Modified Lead-Free Piezoelectric BZT-xBCT System with Higher T C[J].JournalofPhysicsD:AppliedPhysics, 2010， 43(46): 465 401.

[21] Yao Y,etal. Large Piezoelectricity and Dielectric Permittivity in BaTiO3-xBaSnO3System: the Role of Phase Coexisting[J].EurophysicsLetters, 2012， 98(2): 27 008.

[22] Sergienko I,etal. Phenomenological Theory of Phase Transitions in Highly Piezoelectric Perovskites[J].PhysRevB, 2002, 65(14): 144 104.

[23] Vanderbilt D, Cohen M H. Monoclinic and Triclinic Phases in Higher-Order Devonshire Theory[J].PhysRevB, 2001， 63(9): 094 108.

[24] Khachaturyan A G. Ferroelectric Solid Solutions with Morphotropic Boundary: Rotational Instability of Polarization, Metastable Coexistence of Phases and Nanodomain Adaptive States[J].PhilosophicalMagazine, 2010， 90(1): 37-60.

[25] Rossetti G A,etal. Ferroelectric Solid Solutions with Morphotropic Boundaries: Vanishing Polarization Anisotropy, Adaptive, Polar Glass, and Two-Phase States[J].JApplPhys, 2008， 103(11): 114 113.

[26] George A， Rossetti J， Khachaturyan A G. Inherent Nanoscale Structural Instabilities near Morphotropic Boundaries in Ferroelectric Solid Solutions[J].ApplPhysLett, 2007， 91(7): 072 909.

[27] Landau L. The Theory of Phase Transitions[J].Nature, 1936, 138(3 498): 840-841.

[28] Devonshire A. Theory of Ferroelectrics[J].AdvPhys, 1954, 3(10): 85-130.

[29] La-Orauttapong D,etal. Phase Diagram of the Relaxor Ferroelectric (1-x)Pb(Zn_{1/3}Nb_{2/3})O_{3}-xPbTiO_{3}[J].PhysRevB, 2002, 65(14): 144 101.

[30] Noheda B, Cox D E. Bridging Phases at the Morphotropic Boundaries of Lead Oxide Solid Solutions[J].PhaseTransitions, 2006, 79(1-2): 5-20.

[31] Damjanovic D,etal. What Can be Expected from Lead-Free Piezoelectric Materials?[J].FunctMaterLett, 2010, 3(4): 5-13.

[32] Damjanovic D,etal. Elastic, Dielectric, and Piezoelectric Anomalies and Raman Spectroscopy of 0.5Ba(Ti[sub 0.8]Zr[sub 0.2])O[sub 3]-0.5(Ba[sub 0.7]Ca[sub 0.3])TiO[sub 3][J].ApplPhysLett, 2012, 100(19): 192 907.

[33] Zuo R, Fu J. Rhombohedral-Tetragonal Phase Coexistence and Piezoelectric Properties of (NaK)(NbSb) O3-LiTaO3-BaZrO3Lead-Free Ceramics[J].JAmCeramSoc, 2011, 94(5): 1 467-1 470.